突破算法迷宫:精选50道-算法刷题指南
前言
在计算机科学和编程领域,算法和数据结构是基础的概念,无论你是一名初学者还是有经验的开发者,都需要掌握它们。本文将带你深入了解一系列常见的算法和数据结构问题,包括二分查找、滑动窗口、链表、二叉树、TopK、设计题、动态规划等。我们将针对每个问题提供解释和代码示例,以帮助你更好地理解和应用这些概念。
个人题解GitHub连接:LeetCode-Go-Python-Java-C
本文部分内容来自网上搜集与个人实践。如果任何信息存在错误,欢迎读者批评指正。本文仅用于学习交流,不用作任何商业用途。
欢迎订阅专栏,每日一题,和博主一起进步
LeetCode专栏
文章目录
- 前言
- 相关题型
- 基础知识回顾
- 1. 二分查找
- 算法原理
- 实现示例
- 2. 滑动窗口
- 滑动窗口的基本概念
- 滑动窗口的最大值问题
- 滑动窗口的中位数问题
- 最长不含重复字符的子字符串问题
- 3. 数组
- 合并两个有序数组
- 数组中出现超过一半的数问题
- 岛屿的最大面积问题
- 接雨水问题
- 螺旋矩阵问题
- 逆序对问题
- 4. 链表
- 反转链表
- k个一组反转链表
- 删除排序链表中的重复元素
- 环形链表问题
- 两个链表的第一个公共节点问题
- 合并有序链表问题
- 链表求和问题
- 回文链表问题
- 复制带随机指针的链表问题
- 5. 二叉树
- 二叉树的深度
- 之字形打印二叉树问题
- 二叉搜索树的第 k 大节点问题
- 二叉树的最近公共祖先问题
- 二叉树中和为某一值的路径问题
- 二叉树的最大路径和问题
- 二叉树的右视图问题
- 6. TopK
- 最小的k个数问题
- 数组中的第K个最大元素问题
- 7. 设计题
- 最小栈问题
- 两个栈实现队列问题
- LRU缓存机制问题
- 8. 动态规划
- 青蛙跳台阶问题
- 最长上升子序列问题
- 最长公共子序列问题
- 编辑距离问题
- 零钱兑换2问题
- 9. 其他
- 翻转单词顺序问题
- 二进制中1的个数问题
- 颠倒二进制位问题
- 数据流中的中位数问题
- 复原IP地址问题
- 10. 系列题
- X数之和系列
- 两数之和问题
- 三数之和问题
- 最接近的三数之和问题
- 股票系列
- 买卖股票的最佳时机1问题
- 买卖股票的最佳时机2问题
- 买卖股票的最佳时机3问题
- 括号系列
- 有效括号问题
- 最长有效括号问题
- 总结
相关题型
-
二分查找
- 算法原理:二分查找
- 实现示例:求平方根
-
滑动窗口
- 滑动窗口的最大值问题:滑动窗口最大值问题
- 滑动窗口的中位数问题:滑动窗口中位数问题
- 最长不含重复字符的子字符串问题:无重复字符的最长子串
-
数组
- 合并两个有序数组:合并两个有序数组
- 数组中出现超过一半的数问题:多数元素
- 岛屿的最大面积问题:岛屿的最大面积
- 接雨水问题:接雨水
- 螺旋矩阵问题:螺旋矩阵
- 逆序对问题:数组中的逆序对
-
链表
- 反转链表:反转链表
- k个一组反转链表:K 个一组翻转链表
- 删除排序链表中的重复元素:删除排序链表中的重复元素
- 环形链表问题:环形链表
- 两个链表的第一个公共节点问题:相交链表
- 合并有序链表问题:合并两个有序链表
- 链表求和问题:两数相加
- 回文链表问题:回文链表
- 复制带随机指针的链表问题:复制带随机指针的链表
-
二叉树
- 二叉树的深度:二叉树的深度
- 之字形打印二叉树问题:二叉树的锯齿形层序遍历
- 二叉搜索树的第 k 大节点问题:二叉搜索树的第k大节点
- 二叉树的最近公共祖先问题:二叉树的最近公共祖先
- 二叉树中和为某一值的路径问题:二叉树中和为某一值的路径
- 二叉树的最大路径和问题:二叉树中的最大路径和
- 二叉树的右视图问题:二叉树的右视图
-
TopK
- 最小的k个数问题:最小的k个数
- 数组中的第K个最大元素问题:数组中的第K个最大元素
-
设计题
- 最小栈问题:最小栈
- 两个栈实现队列问题:用两个栈实现队列
- LRU缓存机制问题:LRU缓存机制
-
动态规划
- 青蛙跳台阶问题:青蛙跳台阶问题
- 最长上升子序列问题:最长上升子序列
- 最长公共子序列问题:最长公共子序列
- 编辑距离问题:编辑距离
- 零钱兑换2问题:零钱兑换 II
-
其他
- 翻转单词顺序问题:翻转字符串里的单词
- 二进制中1的个数问题:位1的个数
- 颠倒二进制位问题:颠倒二进制位
- 数据流中的中位数问题:数据流中的中位数
- 复原IP地址问题:复原IP地址
-
系列题
-
X数之和系列
- 两数之和问题:两数之和
- 三数之和问题:三数之和
- 最接近的三数之和问题:最接近的三数之和
-
股票系列
- 买卖股票的最佳时机1问题:买卖股票的最佳时机
- 买卖股票的最佳时机2问题:买卖股票的最佳时机 II
- 买卖股票的最佳时机3问题:买卖股票的最佳时机 III
-
括号系列
- 有效括号问题:有效的括号
- 最长有效括号问题:最长有效括号
-
基础知识回顾
1. 二分查找
算法原理
二分查找是一种高效的搜索算法,适用于有序数组。其原理基于不断缩小搜索范围的思想。步骤如下:
- 确定搜索范围的左边界
left和右边界right。 - 计算中间元素的索引
mid,并获取中间元素的值mid_value。 - 如果
mid_value等于目标值,则返回mid。 - 如果
mid_value大于目标值,则将right更新为mid - 1,缩小搜索范围到左半部分。 - 如果
mid_value小于目标值,则将left更新为mid + 1,缩小搜索范围到右半部分。 - 重复步骤 2 到 5,直到找到目标值或搜索范围为空。
实现示例
以下是二分查找的示例代码(Python):
def binary_search(nums, target):left, right = 0, len(nums) - 1while left <= right:mid = left + (right - left) // 2mid_value = nums[mid]if mid_value == target:return midelif mid_value > target:right = mid - 1else:left = mid + 1return -1 # 目标值不存在# 示例用法
nums = [1, 3, 5, 7, 9]
target = 5
result = binary_search(nums, target)
if result != -1:print(f"目标值 {target} 在索引 {result} 处找到。")
else:print("目标值不存在。")
2. 滑动窗口
滑动窗口的基本概念
滑动窗口算法是一种用于处理连续子数组或子字符串的问题的有效方法。它通过维护一个可变大小的窗口来在数据流中移动,并执行相关操作。
滑动窗口的最大值问题
滑动窗口的最大值问题是在给定一个数组和一个固定大小的窗口,找到每个窗口在数组中的最大值。这可以通过双端队列(deque)来实现,保持队列中的元素按降序排列。
from collections import dequedef max_sliding_window(nums, k):result = []window = deque()for i, num in enumerate(nums):# 移除窗口左侧超出窗口大小的元素while window and window[0] < i - k + 1:window.popleft()# 从窗口右侧移除所有小于当前元素的元素while window and nums[window[-1]] < num:window.pop()window.append(i)# 当窗口达到大小k时,将最大值加入结果列表if i >= k - 1:result.append(nums[window[0]])return result# 示例用法
nums = [1, 3, -1, -3, 5, 3, 6, 7]
k = 3
result = max_sliding_window(nums, k)
print(result) # 输出:[3, 3, 5, 5, 6, 7]
滑动窗口的中位数问题
在滑动窗口中找到中位数需要维护一个有序数据结构,例如平衡二叉搜索树(AVL树)或两个堆(最大堆和最小堆)。通过将数据分为两半,分别存储在两个堆中,可以在O(1)时间内找到中位数。
import heapqclass MedianFinder:def __init__(self):self.min_heap = [] # 存储较大一半的元素self.max_heap = [] # 存储较小一半的元素def addNum(self, num):if not self.max_heap or num <= -self.max_heap[0]:heapq.heappush(self.max_heap, -num)else:heapq.heappush(self.min_heap, num)# 保持两个堆的大小平衡if len(self.max_heap) > len(self.min_heap) + 1:heapq.heappush(self.min_heap, -heapq.heappop(self.max_heap))elif len(self.min_heap) > len(self.max_heap):heapq.heappush(self.max_heap, -heapq.heappop(self.min_heap))def findMedian(self):if len(self.max_heap) == len(self.min_heap):return (-self.max_heap[0] + self.min_heap[0]) / 2.0else:return -self.max_heap[0]# 示例用法
median_finder = MedianFinder()
median_finder.addNum(1)
median_finder.addNum(2)
median_finder.addNum(3)
median = median_finder.findMedian()
print(median) # 输出:2.0
1- 有序列表解法
from sortedcontainers import SortedListclass Solution:def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:res = [] # 存放结果的列表m = SortedList() # 使用SortedList维护窗口内的元素for i, num in enumerate(nums):if i >= k:m.remove(nums[i - k]) # 移除窗口最左侧的元素m.add(num) # 将新元素添加到窗口if i - k + 1 >= 0:if not k % 2:# 如果窗口大小为偶数,计算中位数并添加到结果res.append((m[len(m) // 2 - 1] + m[len(m) // 2]) / 2)else:# 如果窗口大小为奇数,直接添加中位数到结果res.append(m[len(m) // 2])return res
from sortedcontainers import SortedListclass Solution:def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:result = []window = SortedList(nums[:k]) # 使用SortedList维护窗口内的元素for i in range(k, len(nums)):# 计算中位数并添加到结果集median = (window[k // 2] + window[(k - 1) // 2]) / 2.0result.append(median)window.add(nums[i]) # 将新元素添加到窗口window.remove(nums[i - k]) # 移除窗口最左侧的元素# 处理最后一个窗口median = (window[k // 2] + window[(k - 1) // 2]) / 2.0result.append(median)return result
2- 堆解法
import heapqclass Solution:def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:if k == 1:return [float(num) for num in nums] # 如果窗口大小为1,直接返回每个元素的浮点数形式的列表res = [] # 存储中位数的结果列表mid_cnt = k // 2 # 窗口的中位数索引# 初始化两个堆,info1用于存储较大一半的元素(负值),info2用于存储较小一半的元素info1 = [(-num, i) for i, num in enumerate(nums[:mid_cnt])]info2 = []heapq.heapify(info1) # 将info1转化为最小堆def get_median(info1, info2, k):# 辅助函数,计算中位数if k % 2 == 0:return (-info1[0][0] + info2[0][0]) / 2.0else:return float(info2[0][0])# 初始窗口滑动过程for i in range(mid_cnt, k):if nums[i] < -info1[0][0]:num, j = heapq.heappop(info1) # 弹出info1的堆顶元素heapq.heappush(info2, (-num, j)) # 将弹出的元素加入info2heapq.heappush(info1, (-nums[i], i)) # 将新元素加入info1else:heapq.heappush(info2, (nums[i], i)) # 将新元素加入info2res.append(get_median(info1, info2, k)) # 计算并添加初始窗口的中位数i = kwhile i < len(nums):num, j = nums[i - k], i - k # 要移出窗口的元素和其索引if num <= -info1[0][0]:if nums[i] < info2[0][0]:heapq.heappush(info1, (-nums[i], i)) # 新元素加入info1else:num1, i1 = info2[0]heapq.heappush(info1, (-num1, i1)) # info2的堆顶元素加入info1heapq.heapreplace(info2, (nums[i], i)) # 弹出info2的堆顶并加入新元素else:if nums[i] < -info1[0][0]:num1, i1 = info1[0]heapq.heappush(info2, (-num1, i1)) # info1的堆顶元素加入info2heapq.heapreplace(info1, (-nums[i], i)) # 弹出info1的堆顶并加入新元素else:heapq.heappush(info2, (nums[i], i)) # 新元素加入info2while info1[0][1] <= j:heapq.heappop(info1) # 移出info1中已经不在窗口中的元素while info2[0][1] <= j:heapq.heappop(info2) # 移出info2中已经不在窗口中的元素res.append(get_median(info1, info2, k)) # 计算并添加当前窗口的中位数i += 1 # 窗口右移一位return res最长不含重复字符的子字符串问题
最长不含重复字符的子字符串问题是要找到一个字符串中的最长子字符串,该子字符串中不包含重复字符。这可以通过使用滑动窗口来解决,同时使用哈希表来记录字符出现的位置。
def length_of_longest_substring(s):if not s:return 0char_index_map = {} # 记录字符的最后出现位置max_length = 0start = 0for end in range(len(s)):if s[end] in char_index_map and char_index_map[s[end]] >= start:start = char_index_map[s[end]] + 1char_index_map[s[end]] = endmax_length = max(max_length, end - start + 1)return max_length# 示例用法
s = "abcabcbb"
length = length_of_longest_substring(s)
print(length) # 输出:3,对应的最长子字符串是 "abc"s = "bbbbb"
length = length_of_longest_substring(s)
print(length) # 输出:1,对应的最长子字符串是 "b"s = "pwwkew"
length = length_of_longest_substring(s)
print(length) # 输出:3,对应的最长子字符串是 "wke"
以上是关于滑动窗口和最长不含重复字符的子字符串问题的简要示例。这些问题是滑动窗口算法的典型应用之一,用于解决多种字符串处理问题。希望这些示例有助于理解滑动窗口算法的核心思想和应用方式。
3. 数组
合并两个有序数组
合并两个有序数组是一个常见的问题,可以使用双指针法来实现。首先将两个数组合并到一个新的数组中,然后对新数组进行排序。
def merge_sorted_arrays(nums1, m, nums2, n):i, j, k = m - 1, n - 1, m + n - 1while i >= 0 and j >= 0:if nums1[i] > nums2[j]:nums1[k] = nums1[i]i -= 1else:nums1[k] = nums2[j]j -= 1k -= 1while j >= 0:nums1[k] = nums2[j]j -= 1k -= 1# 示例用法
nums1 = [1, 2, 3, 0, 0, 0]
m = 3
nums2 = [2, 5, 6]
n = 3
merge_sorted_arrays(nums1, m, nums2, n)
print(nums1) # 输出:[1, 2, 2, 3, 5, 6]
数组中出现超过一半的数问题
在一个数组中找到出现次数超过一半的元素可以使用摩尔投票算法。该算法通过维护候选元素和计数器,来找到可能的众数。
def majority_element(nums):candidate = Nonecount = 0for num in nums:if count == 0:candidate = numcount += 1 if num == candidate else -1return candidate# 示例用法
nums = [2, 2, 1, 1, 1, 2, 2]
majority = majority_element(nums)
print(majority) # 输出:2
岛屿的最大面积问题
在一个二维数组中找到最大的岛屿面积可以使用深度优先搜索(DFS)算法来实现。遍历每个元素,当遇到岛屿时,进行DFS搜索并计算岛屿的面积。
def max_area_of_island(grid):def dfs(row, col):if row < 0 or row >= len(grid) or col < 0 or col >= len(grid[0]) or grid[row][col] == 0:return 0grid[row][col] = 0 # 将已访问的岛屿标记为0area = 1# 递归搜索四个方向area += dfs(row - 1, col)area += dfs(row + 1, col)area += dfs(row, col - 1)area += dfs(row, col + 1)return areamax_area = 0for row in range(len(grid)):for col in range(len(grid[0])):if grid[row][col] == 1:max_area = max(max_area, dfs(row, col))return max_area# 示例用法
grid = [[1, 1, 0, 0, 0],[1, 1, 0, 0, 0],[0, 0, 0, 1, 1],[0, 0, 0, 1, 1]
]
max_area = max_area_of_island(grid)
print(max_area) # 输出:4
接雨水问题
接雨水问题可以使用双指针法来解决。通过维护两个指针和两个变量来计算每个位置可以接的雨水量。
def trap(height):left, right = 0, len(height) - 1left_max, right_max = 0, 0water = 0while left < right:if height[left] < height[right]:if height[left] >= left_max:left_max = height[left]else:water += left_max - height[left]left += 1else:if height[right] >= right_max:right_max = height[right]else:water += right_max - height[right]right -= 1return water# 示例用法
height = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]
rainwater = trap(height)
print(rainwater) # 输出:6
螺旋矩阵问题
螺旋矩阵问题是要按照螺旋的顺序遍历一个二维矩阵。可以使用模拟遍历的方法,逐层遍历矩阵,并按照螺旋顺序添加元素。
def spiral_order(matrix):if not matrix:return []rows, cols = len(matrix), len(matrix[0])result = []left, right, top, bottom = 0, cols - 1, 0, rows - 1while left <= right and top <= bottom:# 从左到右for col in range(left, right + 1):result.append(matrix[top][col])# 从上到下for row in range(top + 1, bottom + 1):result.append(matrix[row][right])# 从右到左,确保不重复遍历同一行或同一列if left < right and top < bottom:for col in range(right - 1, left, -1):result.append(matrix[bottom][col])for row in range(bottom, top, -1):result.append(matrix[row][left])left += 1right -= 1top += 1bottom -= 1return result# 示例用法
matrix = [[1, 2, 3],[4, 5, 6],[7, 8, 9]
]
spiral_order_result = spiral_order(matrix)
print(spiral_order_result) # 输出:[1, 2, 3, 6, 9, 8, 7, 4, 5]
逆序对问题
逆序对问题是要计算一个数组中的逆序对数量,即在数组中找到满足 i < j 且 nums[i] > nums[j] 的 (i, j) 对的数量。可以使用归并排序的思想来解决。
def reverse_pairs(nums):def merge_sort(nums, left, right):if left >= right:return 0mid = left + (right - left) // 2count = merge_sort(nums, left, mid) + merge_sort(nums, mid + 1, right)# 统计逆序对数量i, j = left, mid + 1while i <= mid:while j <= right and nums[i] > 2 * nums[j]:j += 1count += j - (mid + 1)i += 1# 归并排序temp = []i, j = left, mid + 1while i <= mid and j <= right:if nums[i] <= nums[j]:temp.append(nums[i])i += 1else:temp.append(nums[j])j += 1temp.extend(nums[i:mid + 1])temp.extend(nums[j:right + 1])nums[left:right + 1] = tempreturn countreturn merge_sort(nums, 0, len(nums) - 1)# 示例用法
nums = [7, 5, 6, 4]
reverse_pair_count = reverse_pairs(nums)
print(reverse_pair_count) # 输出:5,包含的逆序对为 (7, 5), (7, 6), (7, 4), (5, 4), (6, 4)
4. 链表
反转链表
链表反转是一个常见的操作,可以使用迭代或递归方法来实现。
class ListNode:def __init__(self, val=0, next=None):self.val = valself.next = nextdef reverse_linked_list(head):prev, current = None, headwhile current is not None:next_node = current.nextcurrent.next = prevprev = currentcurrent = next_nodereturn prev# 示例用法
# 创建一个链表:1 -> 2 -> 3 -> 4 -> 5
head = ListNode(1)
current = head
for i in range(2, 6):current.next = ListNode(i)current = current.nextreversed_head = reverse_linked_list(head)# 输出反转后的链表:5 -> 4 -> 3 -> 2 -> 1
while reversed_head is not None:print(reversed_head.val, end=" -> ")reversed_head = reversed_head.next
k个一组反转链表
将链表按照每k个节点一组进行反转是一个常见的链表操作。
class ListNode:def __init__(self, val=0, next=None):self.val = valself.next = nextdef reverse_k_group(head, k):def reverse_linked_list(head):prev, current = None, headwhile current is not None:next_node = current.nextcurrent.next = prevprev = currentcurrent = next_nodereturn prevdef get_kth_node(head, k):for i in range(k):if head is None:return Nonehead = head.nextreturn headdummy = ListNode(0)dummy.next = headprev_group_tail = dummywhile True:group_start = prev_group_tail.nextgroup_end = get_kth_node(group_start, k)if group_end is None:breaknext_group_start = group_end.nextgroup_end.next = None # 切断当前组的链表prev_group_tail.next = reverse_linked_list(group_start)group_start.next = next_group_startprev_group_tail = group_startreturn dummy.next# 示例用法
# 创建一个链表:1 -> 2 -> 3 -> 4 -> 5
head = ListNode(1)
current = head
for i in range(2, 6):current.next = ListNode(i)current = current.nextk = 3
reversed_head = reverse_k_group(head, k)# 输出反转后的链表:3 -> 2 -> 1 -> 4 -> 5
while reversed_head is not None:print(reversed_head.val, end=" -> ")reversed_head = reversed_head.next
删除排序链表中的重复元素
删除排序链表中的重复节点是一个简单的链表操作,可以使用迭代方法实现。
class ListNode:def __init__(self, val=0, next=None):self.val = valself.next = nextdef delete_duplicates(head):current = headwhile current is not None and current.next is not None:if current.val == current.next.val:current.next = current.next.nextelse:current = current.nextreturn head# 示例用法
# 创建一个排序链表:1 -> 1 -> 2 -> 3 -> 3
head = ListNode(1)
head.next = ListNode(1)
head.next.next = ListNode(2)
head.next.next.next = ListNode(3)
head.next.next.next.next = ListNode(3)new_head = delete_duplicates(head)# 输出去重后的链表:1 -> 2 -> 3
while new_head is not None:print(new_head.val, end=" -> ")new_head = new_head.next
环形链表问题
检测链表中是否存在环可以使用快慢指针法来实现。快指针每次移动两步,慢指针每次移动一步,如果存在环,两个指针最终会相遇。
class ListNode:def __init__(self, val=0, next=None):self.val = valself.next = nextdef has_cycle(head):if not head or not head.next:return Falseslow = headfast = head.nextwhile slow != fast:if not fast or not fast.next:return Falseslow = slow.nextfast = fast.next.nextreturn True# 示例用法
# 创建一个带环的链表:1 -> 2 -> 3 -> 4 -> 5 -> 2 (重复节点2形成环)
head = ListNode(1)
current = head
for i in range(2, 6):current.next = ListNode(i)current = current.next
cycle_start = head.nextcurrent.next = cycle_start # 形成环has_cycle_result = has_cycle(head)
print(has_cycle_result) # 输出:True
两个链表的第一个公共节点问题
找到两个链表的第一个公共节点可以使用双指针法来实现。首先计算两个链表的长度差,然后让较长的链表先移动长度差个节点,最后同时移动两个链表找到公共节点。
class ListNode:def __init__(self, val=0, next=None):self.val = valself.next = nextdef get_intersection_node(headA, headB):def get_length(head):length = 0while head is not None:length += 1head = head.nextreturn lengthlenA, lenB = get_length(headA), get_length(headB)# 让较长的链表先移动长度差个节点while lenA > lenB:headA = headA.nextlenA -= 1while lenB > lenA:headB = headB.nextlenB -= 1# 同时移动两个链表,找到第一个公共节点while headA != headB:headA = headA.nextheadB = headB.nextreturn headA# 示例用法
# 创建两个链表:
# 链表A:1 -> 2 -> 3
# 链表B:6 -> 7
# 公共节点:4 -> 5
headA = ListNode(1)
headA.next = ListNode(2)
headA.next.next = ListNode(3)headB = ListNode(6)
headB.next = ListNode(7)common_node = ListNode(4)
common_node.next = ListNode(5)headA.next.next.next = common_node
headB.next.next = common_nodeintersection_node = get_intersection_node(headA, headB)
print(intersection_node.val) # 输出:4
合并有序链表问题
合并两个有序链表可以使用递归或迭代方法来实现。
class ListNode:def __init__(self, val=0, next=None):self.val = valself.next = nextdef merge_sorted_lists(l1, l2):dummy = ListNode(0)current = dummywhile l1 is not None and l2 is not None:if l1.val < l2.val:current.next = l1l1 = l1.nextelse:current.next = l2l2 = l2.nextcurrent = current.nextif l1 is not None:current.next = l1if l2 is not None:current.next = l2return dummy.next# 示例用法
# 创建两个有序链表:
# 链表1:1 -> 2 -> 4
# 链表2:1 -> 3 -> 4
head1 = ListNode(1)
head1.next = ListNode(2)
head1.next.next = ListNode(4)head2 = ListNode(1)
head2.next = ListNode(3)
head2.next.next = ListNode(4)merged_head = merge_sorted_lists(head1, head2)# 输出合并后的有序链表:1 -> 1 -> 2 -> 3 -> 4 -> 4
while merged_head is not None:print(merged_head.val, end=" -> ")merged_head = merged_head.next
链表求和问题
将两个链表表示的整数相加可以使用递归或迭代方法来实现,模拟从低位到高位的加法操作。
class ListNode:def __init__(self, val=0, next=None):self.val = valself.next = nextdef add_two_numbers(l1, l2):dummy = ListNode(0)current = dummycarry = 0while l1 is not None or l2 is not None:x = l1.val if l1 is not None else 0y = l2.val if l2 is not None else 0total = x + y + carrycarry = total // 10current.next = ListNode(total % 10)current = current.nextif l1 is not None:l1 = l1.nextif l2 is not None:l2 = l2.nextif carry > 0:current.next = ListNode(carry)return dummy.next# 示例用法
# 创建两个链表表示的整数:
# 链表1:2 -> 4 -> 3 (表示整数 342)
# 链表2:5 -> 6 -> 4 (表示整数 465)
head1 = ListNode(2)
head1.next = ListNode(4)
head1.next.next = ListNode(3)head2 = ListNode(5)
head2.next = ListNode(6)
head2.next.next = ListNode(4)result_head = add_two_numbers(head1, head2)# 输出相加后的链表表示的整数:7 -> 0 -> 8 (表示整数 807)
while result_head is not None:print(result_head.val, end=" -> ")result_head = result_head.next
回文链表问题
判断一个链表是否是回文链表可以使用快慢指针和链表反转的方法来实现。首先使用快慢指针找到链表的中点,然后反转后半部分链表,最后比较两部分链表是否相等。
class ListNode:def __init__(self, val=0, next=None):self.val = valself.next = nextdef is_palindrome(head):def reverse_linked_list(head):prev, current = None, headwhile current is not None:next_node = current.nextcurrent.next = prevprev = currentcurrent = next_nodereturn prevslow, fast = head, head# 快慢指针找到中点while fast is not None and fast.next is not None:slow = slow.nextfast = fast.next.next# 反转后半部分链表second_half = reverse_linked_list(slow)# 比较两部分链表是否相等while second_half is not None:if head.val != second_half.val:return Falsehead = head.nextsecond_half = second_half.nextreturn True# 示例用法
# 创建一个回文链表:1 -> 2 -> 2 -> 1
head = ListNode(1)
head.next = ListNode(2)
head.next.next = ListNode(2)
head.next.next.next = ListNode(1)is_palindrome_result = is_palindrome(head)
print(is_palindrome_result) # 输出:True
复制带随机指针的链表问题
复制带有随机指针的链表可以使用哈希表来实现,或者可以通过多次遍历链表来完成。
class Node:def __init__(self, val=None, next=None, random=None):self.val = valself.next = nextself.random = randomdef copy_random_list(head):if not head:return None# 创建一个哈希表,用于存储原节点和对应的复制节点的映射关系mapping = {}current = head# 第一次遍历:复制链表节点,不处理random指针while current:mapping[current] = Node(current.val)current = current.nextcurrent = head# 第二次遍历:处理复制节点的random指针while current:if current.next:mapping[current].next = mapping[current.next]if current.random:mapping[current].random = mapping[current.random]current = current.nextreturn mapping[head]# 示例用法
# 创建一个带随机指针的链表:
# 1 -> 2 -> 3
# | |
# v v
# 3 -> 1
node1 = Node(1)
node2 = Node(2)
node3 = Node(3)node1.next = node2
node1.random = node3
node2.next = node3
node2.random = node1
node3.random = node1copied_head = copy_random_list(node1)# 输出复制后的带随机指针的链表:
# 1 -> 2 -> 3
# | |
# v v
# 3 -> 1
while copied_head:print(f"Value: {copied_head.val}, Random: {copied_head.random.val if copied_head.random else None}")copied_head = copied_head.next
这些是关于链表部分的具体内容示例,涵盖了链表操作中的一些常见问题和解决方法。这些问题涵盖了链表反转、链表分组、删除重复元素、检测环、找到第一个公共节点、合并有序链表、链表求和、判断回文链表以及复制带随机指针的链表等常见问题。
5. 二叉树
二叉树的深度
计算二叉树的深度通常使用递归方法,分别计算左子树和右子树的深度,然后取较大值加1即可。
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef max_depth(root):if not root:return 0left_depth = max_depth(root.left)right_depth = max_depth(root.right)return max(left_depth, right_depth) + 1# 示例用法
# 创建一个二叉树:
# 1
# / \
# 2 3
# / \
# 4 5
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)depth = max_depth(root)
print(depth) # 输出:3
之字形打印二叉树问题
之字形打印二叉树可以使用队列来实现,通过记录当前层的节点,然后按照不同的层次顺序输出节点值。
from collections import dequeclass TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef zigzag_level_order(root):if not root:return []result = []queue = deque([root])reverse = Falsewhile queue:level_values = []level_size = len(queue)for _ in range(level_size):node = queue.popleft()if reverse:level_values.insert(0, node.val)else:level_values.append(node.val)if node.left:queue.append(node.left)if node.right:queue.append(node.right)result.append(level_values)reverse = not reversereturn result# 示例用法
# 创建一个二叉树:
# 3
# / \
# 9 20
# / \
# 15 7
root = TreeNode(3)
root.left = TreeNode(9)
root.right = TreeNode(20)
root.right.left = TreeNode(15)
root.right.right = TreeNode(7)zigzag_result = zigzag_level_order(root)
# 输出之字形顺序的结果:[[3], [20, 9], [15, 7]]
print(zigzag_result)
二叉搜索树的第 k 大节点问题
找到二叉搜索树中第 k 大的节点可以采用中序遍历的变种方法。通过反向中序遍历,先遍历右子树、根节点、左子树,就可以按照降序遍历节点,并找到第 k 大的节点。
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef kth_largest(root, k):def reverse_inorder(node):nonlocal kif not node:return Noneresult = reverse_inorder(node.right)if result is not None:return resultk -= 1if k == 0:return nodereturn reverse_inorder(node.left)return reverse_inorder(root).val# 示例用法
# 创建一个二叉搜索树:
# 3
# / \
# 1 4
# \
# 2
root = TreeNode(3)
root.left = TreeNode(1)
root.left.right = TreeNode(2)
root.right = TreeNode(4)k = 2
kth_largest_node = kth_largest(root, k)
print(kth_largest_node) # 输出:2
二叉树的最近公共祖先问题
找到二叉树中两个节点的最近公共祖先可以使用递归方法来实现。根据最近公共祖先的性质,如果一个节点是两个节点的最近公共祖先,那么这个节点要么是其中一个节点,要么在左子树中,要么在右子树中,通过递归遍历左右子树,找到两个节点的最近公共祖先。
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef lowest_common_ancestor(root, p, q):if not root:return None# 如果根节点是其中一个节点,则返回根节点if root == p or root == q:return rootleft_ancestor = lowest_common_ancestor(root.left, p, q)right_ancestor = lowest_common_ancestor(root.right, p, q)# 如果左子树和右子树都返回非空节点,说明分别找到了p和q,则当前节点是最近公共祖先if left_ancestor and right_ancestor:return root# 如果左子树返回非空节点,则返回左子树的结果return left_ancestor if left_ancestor else right_ancestor# 示例用法
# 创建一个二叉树:
# 3
# / \
# 5 1
# / \ / \
# 6 2 0 8
# / \
# 7 4
root = TreeNode(3)
root.left = TreeNode(5)
root.right = TreeNode(1)
root.left.left = TreeNode(6)
root.left.right = TreeNode(2)
root.left.right.left = TreeNode(7)
root.left.right.right = TreeNode(4)
root.right.left = TreeNode(0)
root.right.right = TreeNode(8)p = root.left # 节点5
q = root.right # 节点1
ancestor = lowest_common_ancestor(root, p, q)
print(ancestor.val) # 输出:3,最近公共祖先是根节点3
二叉树中和为某一值的路径问题
找到二叉树中路径和等于给定值的路径可以使用递归方法来实现。从根节点开始,递归遍历左子树和右子树,并累加路径上的节点值,当遇到叶子节点且路径和等于给定值时,将路径添加到结果中。
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef find_paths(root, target):def dfs(node, current_path, current_sum):if not node:returncurrent_path.append(node.val)current_sum += node.valif not node.left and not node.right and current_sum == target:paths.append(list(current_path))dfs(node.left, current_path, current_sum)dfs(node.right, current_path, current_sum)# 回溯:恢复当前路径状态current_path.pop()paths = []dfs(root, [], 0)return paths# 示例用法
# 创建一个二叉树:
# 5
# / \
# 4 8
# / / \
# 11 13 4
# / \ / \
# 7 2 5 1
root = TreeNode(5)
root.left = TreeNode(4)
root.right = TreeNode(8)
root.left.left = TreeNode(11)
root.right.left = TreeNode(13)
root.right.right = TreeNode(4)
root.left.left.left = TreeNode(7)
root.left.left.right = TreeNode(2)
root.right.right.left = TreeNode(5)
root.right.right.right = TreeNode(1)target = 22
paths = find_paths(root, target)
# 输出路径和为22的所有路径:[[5, 4, 11, 2], [5, 8, 4, 5]]
print(paths)
二叉树的最大路径和问题
找到二叉树中的最大路径和可以使用递归方法来实现。对于每个节点,有四种情况需要考虑:只包含当前节点的路径、包含当前节点和左子树的路径、包含当前节点和右子树的路径、包含当前节点、左子树和右子树的路径。通过递归计算这四种情况的最大值,即可找到最大路径和。
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef max_path_sum(root):def max_gain(node):nonlocal max_sumif not node:return 0# 递归计算左子树和右子树的最大贡献值left_gain = max(max_gain(node.left), 0)right_gain = max(max_gain(node.right), 0)# 计算以当前节点为根的最大路径和current_max_path = node.val + left_gain + right_gain# 更新全局最大路径和max_sum = max(max_sum, current_max_path)# 返回以当前节点为根的最大贡献值return node.val + max(left_gain, right_gain)max_sum = float('-inf')max_gain(root)return max_sum# 示例用法
# 创建一个二叉树:
# -10
# / \
# 9 20
# / \
# 15 7
root = TreeNode(-10)
root.left = TreeNode(9)
root.right = TreeNode(20)
root.right.left = TreeNode(15)
root.right.right = TreeNode(7)max_path = max_path_sum(root)
print(max_path) # 输出:42
二叉树的右视图问题
获取二叉树的右视图可以使用广度优先搜索(BFS)来实现,每一层从右向左取最后一个节点加入结果列表。
from collections import dequeclass TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef right_side_view(root):if not root:return []result = []queue = deque([root])while queue:level_size = len(queue)for i in range(level_size):node = queue.popleft()if i == level_size - 1:result.append(node.val)if node.left:queue.append(node.left)if node.right:queue.append(node.right)return result# 示例用法
# 创建一个二叉树:
# 1
# / \
# 2 3
# \ \
# 5 4
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.right = TreeNode(5)
root.right.right = TreeNode(4)right_view = right_side_view(root)
# 输出右视图:[1, 3, 4]
print(right_view)
6. TopK
最小的k个数问题
找到一个数组中最小的 k 个数可以使用堆(Heap)来实现,维护一个大小为 k 的最大堆,遍历数组,将元素依次加入堆中,当堆的大小超过 k 时,弹出堆顶元素,最终堆中剩下的元素即为最小的 k 个数。
import heapqdef get_least_numbers(arr, k):if k <= 0 or k > len(arr):return []max_heap = []for num in arr:if len(max_heap) < k:heapq.heappush(max_heap, -num)else:if -num > max_heap[0]:heapq.heappop(max_heap)heapq.heappush(max_heap, -num)return [-num for num in max_heap]# 示例用法
arr = [3, 2, 1, 5, 6, 4]
k = 2
least_numbers = get_least_numbers(arr, k)
print(least_numbers) # 输出:[2, 1]
数组中的第K个最大元素问题
找到一个数组中第 k 大的元素也可以使用堆来实现,维护一个大小为 k 的最小堆,遍历数组,将元素依次加入堆中,当堆的大小超过 k 时,弹出堆顶元素,最终堆中剩下的元素即为第 k 大的元素。
import heapqdef find_kth_largest(arr, k):if k <= 0 or k > len(arr):return Nonemin_heap = arr[:k]heapq.heapify(min_heap)for num in arr[k:]:if num > min_heap[0]:heapq.heappop(min_heap)heapq.heappush(min_heap, num)return min_heap[0]# 示例用法
arr = [3, 2, 1, 5, 6, 4]
k = 2
kth_largest = find_kth_largest(arr, k)
print(kth_largest) # 输出:5
这些是关于二叉树和TopK问题的具体内容示例,涵盖了二叉树深度计算、之字形打印二叉树、二叉搜索树的第 k 大节点、二叉树最近公共祖先、二叉树路径和、二叉树最大路径和、二叉树右视图,以及最小的 k 个数和数组中的第 k 个最大元素等问题的解决方法。接下来,我们将继续探讨设计题、动态规划、以及其他一些常见问题的解决方法。
下面是关于设计题和动态规划问题的具体内容:
7. 设计题
最小栈问题
设计一个支持常数时间复杂度的最小栈,可以通过在普通栈中同时维护最小值的方式来实现。每次入栈时,将当前元素与栈顶的最小值进行比较,将较小的值入栈。出栈时,同时弹出栈顶元素和最小值。
class MinStack:def __init__(self):self.stack = []self.min_stack = []def push(self, val):self.stack.append(val)if not self.min_stack or val <= self.min_stack[-1]:self.min_stack.append(val)def pop(self):if self.stack:if self.stack[-1] == self.min_stack[-1]:self.min_stack.pop()self.stack.pop()def top(self):if self.stack:return self.stack[-1]def get_min(self):if self.min_stack:return self.min_stack[-1]# 示例用法
min_stack = MinStack()
min_stack.push(2)
min_stack.push(0)
min_stack.push(3)
min_stack.push(0)print(min_stack.get_min()) # 输出:0
min_stack.pop()
print(min_stack.get_min()) # 输出:0
min_stack.pop()
print(min_stack.get_min()) # 输出:0
min_stack.pop()
print(min_stack.get_min()) # 输出:2
两个栈实现队列问题
通过使用两个栈来实现队列,一个栈用于入队操作,另一个栈用于出队操作。当需要出队时,将入队栈中的元素依次出栈并入到出队栈中,这样出队操作就可以从出队栈中进行。
class MyQueue:def __init__(self):self.in_stack = []self.out_stack = []def push(self, val):self.in_stack.append(val)def pop(self):if not self.out_stack:while self.in_stack:self.out_stack.append(self.in_stack.pop())if self.out_stack:return self.out_stack.pop()def peek(self):if not self.out_stack:while self.in_stack:self.out_stack.append(self.in_stack.pop())if self.out_stack:return self.out_stack[-1]def empty(self):return not self.in_stack and not self.out_stack# 示例用法
queue = MyQueue()
queue.push(1)
queue.push(2)
print(queue.peek()) # 输出:1
print(queue.pop()) # 输出:1
print(queue.empty()) # 输出:False
LRU缓存机制问题
设计和实现LRU(Least Recently Used)缓存机制可以使用哈希表和双向链表来实现。哈希表用于快速查找缓存中的元素,双向链表用于维护元素的访问顺序。
class LRUCache:def __init__(self, capacity):self.capacity = capacityself.cache = {}self.head = Node()self.tail = Node()self.head.next = self.tailself.tail.prev = self.headdef _add_node(self, node):node.prev = self.headnode.next = self.head.nextself.head.next.prev = nodeself.head.next = nodedef _remove_node(self, node):prev = node.prevnext_node = node.nextprev.next = next_nodenext_node.prev = prevdef _move_to_head(self, node):self._remove_node(node)self._add_node(node)def _pop_tail(self):res = self.tail.prevself._remove_node(res)return resdef get(self, key):if key in self.cache:node = self.cache[key]self._move_to_head(node)return node.valuereturn -1def put(self, key, value):if key in self.cache:node = self.cache[key]node.value = valueself._move_to_head(node)else:if len(self.cache) >= self.capacity:tail = self._pop_tail()del self.cache[tail.key]new_node = Node(key, value)self.cache[key] = new_nodeself._add_node(new_node)class Node:def __init__(self, key=None, value=None):self.key = keyself.value = valueself.prev = Noneself.next = None# 示例用法
cache = LRUCache(2)
cache.put(1, 1)
cache.put(2, 2)
print(cache.get(1)) # 输出:1
cache.put(3, 3)
print(cache.get(2)) # 输出:-1,因为键2已被移除
8. 动态规划
青蛙跳台阶问题
青蛙跳台阶问题可以看作是一个典型的动态规划问题,每次可以跳1个或2个台阶,那么跳到第n个台阶的方法数等于跳到第n-1个台阶的方法数加上跳到第n-2个台阶的方法数,即 Fibonacci 数列。
def climb_stairs(n):if n <= 2:return ndp = [0] * (n + 1)dp[1] = 1dp[2] = 2for i in range(3, n + 1):dp[i] = dp[i - 1] + dp[i - 2]return dp[n]# 示例用法
n = 4
ways = climb_stairs(n)
print(ways) # 输出:5
最长上升子序列问题
最长上升子序列问题是一个经典的动态规划问题,可以使用动态规划来解决。定义一个状态数组dp,其中dp[i]表示以第i个元素为结尾的最长上升子序列的长度。初始时,每个元素自成一个长度为1的上升子序列,然后遍历数组,对于每个元素,找到其前面所有比它小的元素,计算以该元素为结尾的最长上升子序列长度。
def length_of_lis(nums):if not nums:return 0n = len(nums)dp = [1] * nfor i in range(1, n):for j in range(i):if nums[i] > nums[j]:dp[i] = max(dp[i], dp[j] + 1)return max(dp)# 示例用法
nums = [10, 9, 2, 5, 3, 7, 101, 18]
length = length_of_lis(nums)
print(length) # 输出:5,最长上升子序列是[2, 3, 7, 101]
最长公共子序列问题
最长公共子序列问题可以使用动态规划来解决。定义一个二维数组dp,其中dp[i][j]表示字符串text1的前i个字符和字符串text2的前j个字符的最长公共子序列的长度。根据动态规划的状态转移方程,可以填充整个dp数组。
def longest_common_subsequence(text1, text2):m, n = len(text1), len(text2)dp = [[0] * (n + 1) for _ in range(m + 1)]for i in range(1, m + 1):for j in range(1, n + 1):if text1[i - 1] == text2[j - 1]:dp[i][j] = dp[i - 1][j - 1] + 1else:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])return dp[m][n]# 示例用法
text1 = "abcde"
text2 = "ace"
length = longest_common_subsequence(text1, text2)
print(length) # 输出:3,最长公共子序列是"ace"
编辑距离问题
编辑距离问题是一个经典的字符串匹配问题,可以使用动态规划来解决。定义一个二维数组dp,其中dp[i][j]表示将字符串word1的前i个字符转换成字符串word2的前j个字符所需的最小编辑距离。通过填充dp数组,可以得到最小编辑距离。
def min_distance(word1, word2):m, n = len(word1), len(word2)dp = [[0] * (n + 1) for _ in range(m + 1)]for i in range(m + 1):for j in range(n + 1):if i == 0:dp[i][j] = jelif j == 0:dp[i][j] = ielif word1[i - 1] == word2[j - 1]:dp[i][j] = dp[i - 1][j - 1]else:dp[i][j] = 1 + min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1])return dp[m][n]# 示例用法
word1 = "horse"
word2 = "ros"
distance = min_distance(word1, word2)
print(distance) # 输出:3,最小编辑距离为3,删除'h',替换'r',添加's'
零钱兑换2问题
零钱兑换2问题是一个动态规划问题,可以通过动态规划来计算不同面额的硬币组合成指定金额的方法数。定义一个一维数组dp,其中dp[i]表示组合成金额i的方法数。初始时,dp[0]为1,表示组合成金额0的方法数为1,其余元素初始化为0,然后遍历硬币面额,更新dp数组。
def change(amount, coins):dp = [0] * (amount + 1)dp[0] = 1for coin in coins:for i in range(coin, amount + 1):dp[i] += dp[i - coin]return dp[amount]# 示例用法
amount = 5
coins = [1, 2, 5]
combinations = change(amount, coins)
print(combinations) # 输出:4,有4种组合方式:[1, 1, 1, 1, 1], [1, 1, 1, 2], [2, 2, 1], [5]
这些是关于设计题和动态规划问题的具体内容示例,涵盖了最小栈、两个栈实现队列、LRU缓存机制、青蛙跳台阶、最长上升子序列、最长公共子序列、编辑距离、零钱兑换2等问题的解决方法。接下来,我们将继续探讨其他一些常见问题的解决方法。
9. 其他
翻转单词顺序问题
翻转单词顺序问题可以通过先将整个字符串翻转,然后再翻转每个单词的字符顺序来实现。
def reverse_words(s):s = s[::-1] # 翻转整个字符串words = s.split() # 切分单词return ' '.join(words[::-1]) # 翻转单词顺序并拼接成字符串# 示例用法
s = "the sky is blue"
reversed_s = reverse_words(s)
print(reversed_s) # 输出:"blue is sky the"
二进制中1的个数问题
计算一个整数的二进制表示中1的个数可以使用位运算来实现,不断将整数右移一位并与1进行与运算,直到整数为0。
def hamming_weight(n):count = 0while n:count += n & 1n >>= 1return count# 示例用法
n = 11
count = hamming_weight(n)
print(count) # 输出:3,二进制表示为1011,含有3个1
颠倒二进制位问题
颠倒一个无符号整数的二进制位可以通过不断将整数的最低位取出并左移,同时将结果的最高位取出并左移,然后将它们进行或运算来实现。
def reverse_bits(n):result = 0for _ in range(32):result <<= 1result |= n & 1n >>= 1return result# 示例用法
n = 43261596
reversed_n = reverse_bits(n)
print(reversed_n) # 输出:964176192
数据流中的中位数问题
设计一个支持在数据流中随时获取中位数的数据结构,可以使用两个堆来实现。一个大顶堆用于存储较小的一半数据,一个小顶堆用于存储较大的一半数据。
import heapqclass MedianFinder:def __init__(self):self.small_heap = [] # 小顶堆,存储较大的一半数据self.large_heap = [] # 大顶堆,存储较小的一半数据def add_num(self, num):if not self.small_heap or num > -self.small_heap[0]:heapq.heappush(self.small_heap, -num)else:heapq.heappush(self.large_heap, num)# 平衡两个堆的大小if len(self.small_heap) > len(self.large_heap) + 1:heapq.heappush(self.large_heap, -heapq.heappop(self.small_heap))elif len(self.large_heap) > len(self.small_heap):heapq.heappush(self.small_heap, -heapq.heappop(self.large_heap))def find_median(self):if len(self.small_heap) == len(self.large_heap):return (-self.small_heap[0] + self.large_heap[0]) / 2.0else:return -self.small_heap[0]# 示例用法
median_finder = MedianFinder()
median_finder.add_num(1)
median_finder.add_num(2)
median_finder.add_num(3)
median = median_finder.find_median()
print(median) # 输出:2.0,因为中位数是2median_finder.add_num(4)
median = median_finder.find_median()
print(median) # 输出:2.5,因为中位数是 (2 + 3) / 2 = 2.5复原IP地址问题
复原IP地址问题是一个回溯算法问题,可以通过回溯算法来列举所有可能的IP地址组合。
def restore_ip_addresses(s):def backtrack(start, path):if len(path) == 4:if start == len(s):result.append('.'.join(path))returnfor i in range(1, 4):if start + i <= len(s):segment = s[start:start + i]if (len(segment) == 1 or (len(segment) > 1 and segment[0] != '0')) and 0 <= int(segment) <= 255:path.append(segment)backtrack(start + i, path)path.pop()result = []backtrack(0, [])return result# 示例用法
s = "25525511135"
ip_addresses = restore_ip_addresses(s)
print(ip_addresses) # 输出:["255.255.11.135", "255.255.111.35"]
这些是关于其他常见问题的解决方法,包括翻转单词顺序、二进制中1的个数、颠倒二进制位、数据流中的中位数、以及复原IP地址等问题的解决方法。接下来,我们将继续探讨一些常见的问题系列。
当然,下面是对系列题中的一些问题的具体内容示例:
10. 系列题
X数之和系列
两数之和问题
两数之和问题是一个常见的问题,可以使用哈希表来解决。遍历数组,对于每个元素,检查目标值与当前元素的差值是否在哈希表中,如果在,则找到了两个数的和等于目标值。
def two_sum(nums, target):num_to_index = {}for i, num in enumerate(nums):complement = target - numif complement in num_to_index:return [num_to_index[complement], i]num_to_index[num] = ireturn None# 示例用法
nums = [2, 7, 11, 15]
target = 9
result = two_sum(nums, target)
print(result) # 输出:[0, 1],因为 nums[0] + nums[1] = 2 + 7 = 9
三数之和问题
三数之和问题可以转化为两数之和问题,先对数组进行排序,然后固定一个数,再使用双指针法找出另外两个数,使它们的和等于目标值。
def three_sum(nums):nums.sort()result = []n = len(nums)for i in range(n - 2):if i > 0 and nums[i] == nums[i - 1]:continueleft, right = i + 1, n - 1while left < right:total = nums[i] + nums[left] + nums[right]if total == 0:result.append([nums[i], nums[left], nums[right]])while left < right and nums[left] == nums[left + 1]:left += 1while left < right and nums[right] == nums[right - 1]:right -= 1left += 1right -= 1elif total < 0:left += 1else:right -= 1return result# 示例用法
nums = [-1, 0, 1, 2, -1, -4]
result = three_sum(nums)
print(result) # 输出:[[-1, -1, 2], [-1, 0, 1]]
最接近的三数之和问题
最接近的三数之和问题是一个变种,可以在求得三个数的和等于目标值的前提下,找出最接近目标值的和。
def three_sum_closest(nums, target):nums.sort()closest_sum = float('inf')min_diff = float('inf')n = len(nums)for i in range(n - 2):left, right = i + 1, n - 1while left < right:total = nums[i] + nums[left] + nums[right]diff = abs(total - target)if diff < min_diff:min_diff = diffclosest_sum = totalif total < target:left += 1elif total > target:right -= 1else:return closest_sumreturn closest_sum# 示例用法
nums = [-1, 2, 1, -4]
target = 1
result = three_sum_closest(nums, target)
print(result) # 输出:2,最接近目标值1的和为2
这些是关于X数之和系列问题的解决方法,包括两数之和、三数之和、最接近的三数之和等问题的解决方法。这些问题涵盖了在数组中查找数的和等于目标值的情况,以及在特定条件下查找满足要求的组合的情况。
股票系列
买卖股票的最佳时机1问题
买卖股票的最佳时机1问题可以通过维护最低股价和最大利润来解决。遍历股价数组,对于每个股价,更新最低股价和最大利润。
def max_profit(prices):min_price = float('inf')max_profit = 0for price in prices:min_price = min(min_price, price)max_profit = max(max_profit, price - min_price)return max_profit# 示例用法
prices = [7, 1, 5, 3, 6, 4]
profit = max_profit(prices)
print(profit) # 输出:5,最大利润为5,买入价格为1,卖出价格为6
买卖股票的最佳时机2问题
买卖股票的最佳时机2问题是一个贪心算法问题,可以通过遍历股价数组,对于每一天,如果股价比前一天高,就将这一天的利润加到总利润上。
def max_profit2(prices):max_profit = 0for i in range(1, len(prices)):if prices[i] > prices[i - 1]:max_profit += prices[i] - prices[i - 1]return max_profit# 示例用法
prices = [7, 1, 5, 3, 6, 4]
profit = max_profit2(prices)
print(profit) # 输出:7,最大利润为7,买入价格为1,卖出价格为5,再买入价格为3,卖出价格为6
买卖股票的最佳时机3问题
买卖股票的最佳时机3问题可以通过动态规划来解决。定义一个二维数组dp,其中dp[i][j][k]表示在第i天结束时,最多进行j次交易并持有(k=1)或不持有(k=0)股票时的最大利润。根据状态转移方程填充dp数组。
def max_profit3(prices):if not prices:return 0max_transactions = 2 # 最多交易次数n = len(prices)dp = [[[0] * 2 for _ in range(max_transactions + 1)] for _ in range(n)]for i in range(n):for j in range(max_transactions, 0, -1):if i == 0:dp[i][j][1] = -prices[i]else:dp[i][j][1] = max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i])dp[i][j][0] = max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i])return dp[n - 1][max_transactions][0]# 示例用法
prices = [3, 3, 5, 0, 0, 3, 1, 4]
profit = max_profit3(prices)
print(profit) # 输出:6,最大利润为6,买入价格为3,卖出价格为5,再买入价格为0,卖出价格为3
这些是关于股票系列问题的解决方法,包括买卖股票的最佳时机1、买卖股票的最佳时机2、买卖股票的最佳时机3等问题的解决方法。这些问题涵盖了股票交易中的不同情况和限制条件,帮助你了解如何在股票市场中做出明智的决策。
括号系列
有效括号问题
有效括号问题是一个栈的经典应用。使用栈来存储左括号,当遇到右括号时,检查栈顶是否与之匹配,如果匹配则出栈,否则不匹配。
def is_valid(s):stack = []mapping = {')': '(', '}': '{', ']': '['}for char in s:if char in mapping:top_element = stack.pop() if stack else '#'if mapping[char] != top_element:return Falseelse:stack.append(char)return not stack# 示例用法
s = "()[]{}"
result = is_valid(s)
print(result) # 输出:True
最长有效括号问题
最长有效括号问题可以通过栈来解决。遍历字符串,使用栈来存储未匹配的左括号的索引,当遇到右括号时,检查栈是否为空,如果不为空,计算当前位置与栈顶元素的距离,这个距离就是当前有效括号的长度。
def longest_valid_parentheses(s):stack = [-1] # 初始化栈,用-1表示栈底max_length = 0for i in range(len(s)):if s[i] == '(':stack.append(i)else:stack.pop()if not stack:stack.append(i)else:max_length = max(max_length, i - stack[-1])return max_length# 示例用法
s = "(()())"
result = longest_valid_parentheses(s)
print(result) # 输出:6,最长有效括号为"(()())"
以上是括号系列问题的解决方法,包括判断有效括号和找到最长有效括号子串。这些问题涉及了括号匹配的常见场景,也是算法和数据结构中的经典问题。
总结
本文深入介绍了一系列常见的算法和数据结构问题,以及它们在LeetCode上的相关题目。这些问题覆盖了计算机科学和编程中的关键概念,包括基本的数据结构、常用的算法思想以及动态规划等。通过学习和实践这些问题,你将能够提升编程技能,更好地应对面试挑战,并能够更高效地解决实际问题。希望本文对你在算法和数据结构领域的学习和发展有所帮助。
相关文章:

突破算法迷宫:精选50道-算法刷题指南
前言 在计算机科学和编程领域,算法和数据结构是基础的概念,无论你是一名初学者还是有经验的开发者,都需要掌握它们。本文将带你深入了解一系列常见的算法和数据结构问题,包括二分查找、滑动窗口、链表、二叉树、TopK、设计题、动…...

玩转Mysql系列 - 第26篇:聊聊mysql如何实现分布式锁?
这是Mysql系列第26篇。 本篇我们使用mysql实现一个分布式锁。 分布式锁的功能 分布式锁使用者位于不同的机器中,锁获取成功之后,才可以对共享资源进行操作 锁具有重入的功能:即一个使用者可以多次获取某个锁 获取锁有超时的功能ÿ…...

linux 解压缩命令tar
Tar tar 命令的选项有很多(用 man tar 可以查看到),但常用的就那么几个选项,下面来举例说明一下: tar -cf all.tar *.jpg 这条命令是将所有.jpg 的文件打成一个名为 all.tar 的包。-c 是表示产生新的包,-f 指 定包的文件名。 …...

OpenAI ChatGPT API 文档之 Embedding
译者注: Embedding 直接翻译为嵌入似乎不太恰当,于是问了一下 ChatGPT,它的回复如下: 在自然语言处理和机器学习领域,"embeddings" 是指将单词、短语或文本转换成连续向量空间的过程。这个向量空间通常被称…...

Java常用类(二)
好久不见,因工作原因,好久没发文了,OldWang 回来了,持续更新Java内容!⭐ 不可变和可变字符序列使用陷阱⭐ 时间处理相关类⭐ Date 时间类(java.util.Date)⭐ DateFormat 类和 SimpleDateFormat 类⭐ Calendar 日历类 ⭐…...
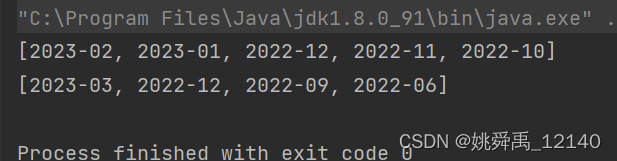
Java获取给定月份的前N个月份和前N个季度
描述: 在项目开发过程中,遇到这样一个需求,即:给定某一月份,得到该月份前面的几个月份以及前面的几个季度。例如:给定2023-09,获取该月份前面的前3个月,即2023-08、2023-07、2023-0…...

网页资源加载过程
网页资源加载是指在浏览器中访问一个网页时,浏览器如何获取和显示网页内容的过程。这个过程通常分为以下几个步骤: DNS 解析: 当用户在浏览器中输入一个网址(例如,https://www.example.com),浏览…...
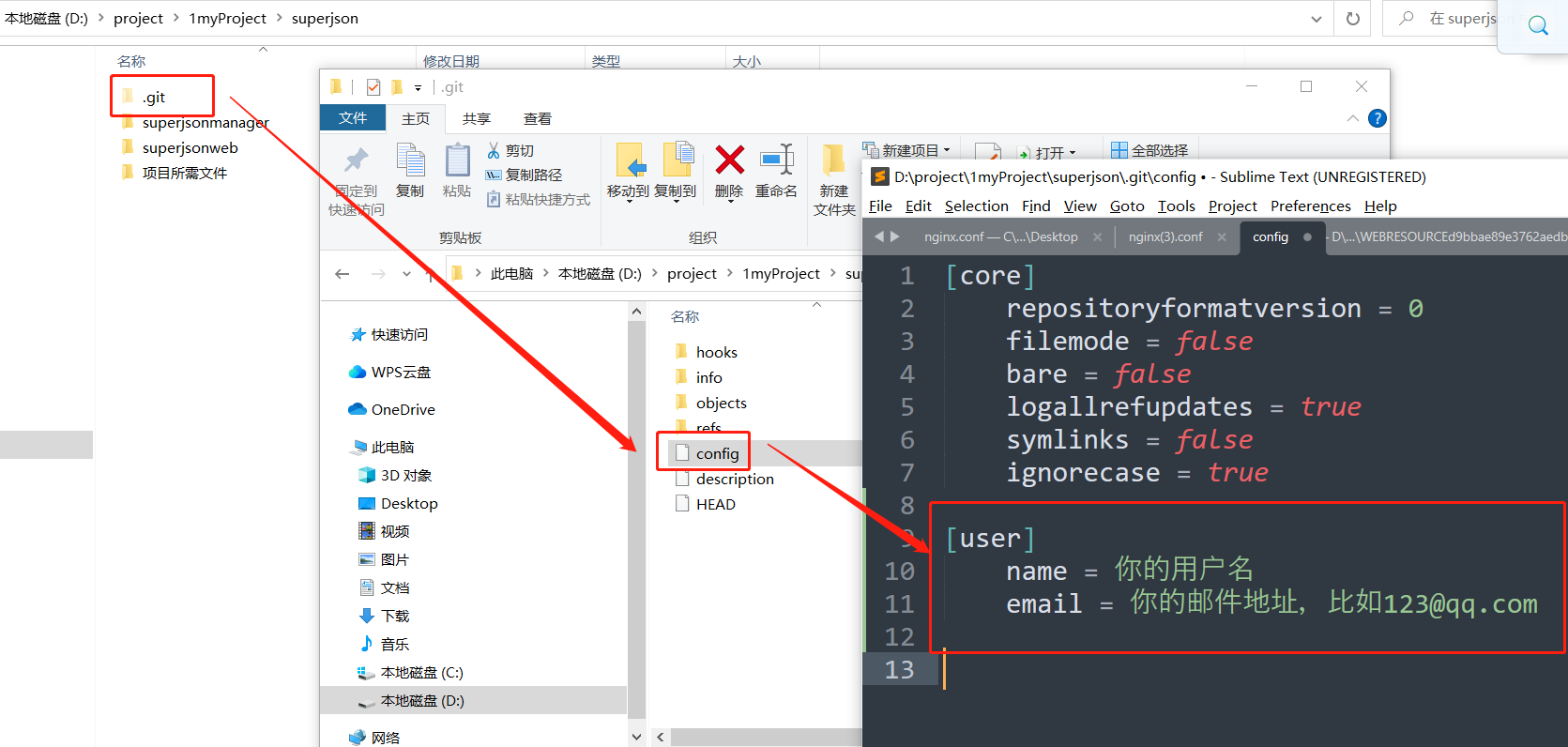
使用git config --global设置用户名和邮件,以及git config的全局和局部配置
文章目录 1. 文章引言2. 全局配置2.1 命令方式2.2 配置文件方式 3. 局部配置3.1 命令方式3.2 配置文件方式 4. 总结 1. 文章引言 我们为什么要设置设置用户名和邮件? 我们在注册github,gitlab等时,一般使用用户名或邮箱: 这个用户…...

【C语言】21-指针-3
目录 1. 指针数组1.1 什么是指针数组1.2 如何定义指针数组1.3 如何使用指针数组2. 多重指针2.1 二重指针的定义2.2 二重指针的初始化与赋值2.3 二重指针的使用3. 指针常量、常量指针、指向常量的常指针3.1 概念3.2 const pointer3.3 pointer to a constant3.3.1 (pointer to a …...
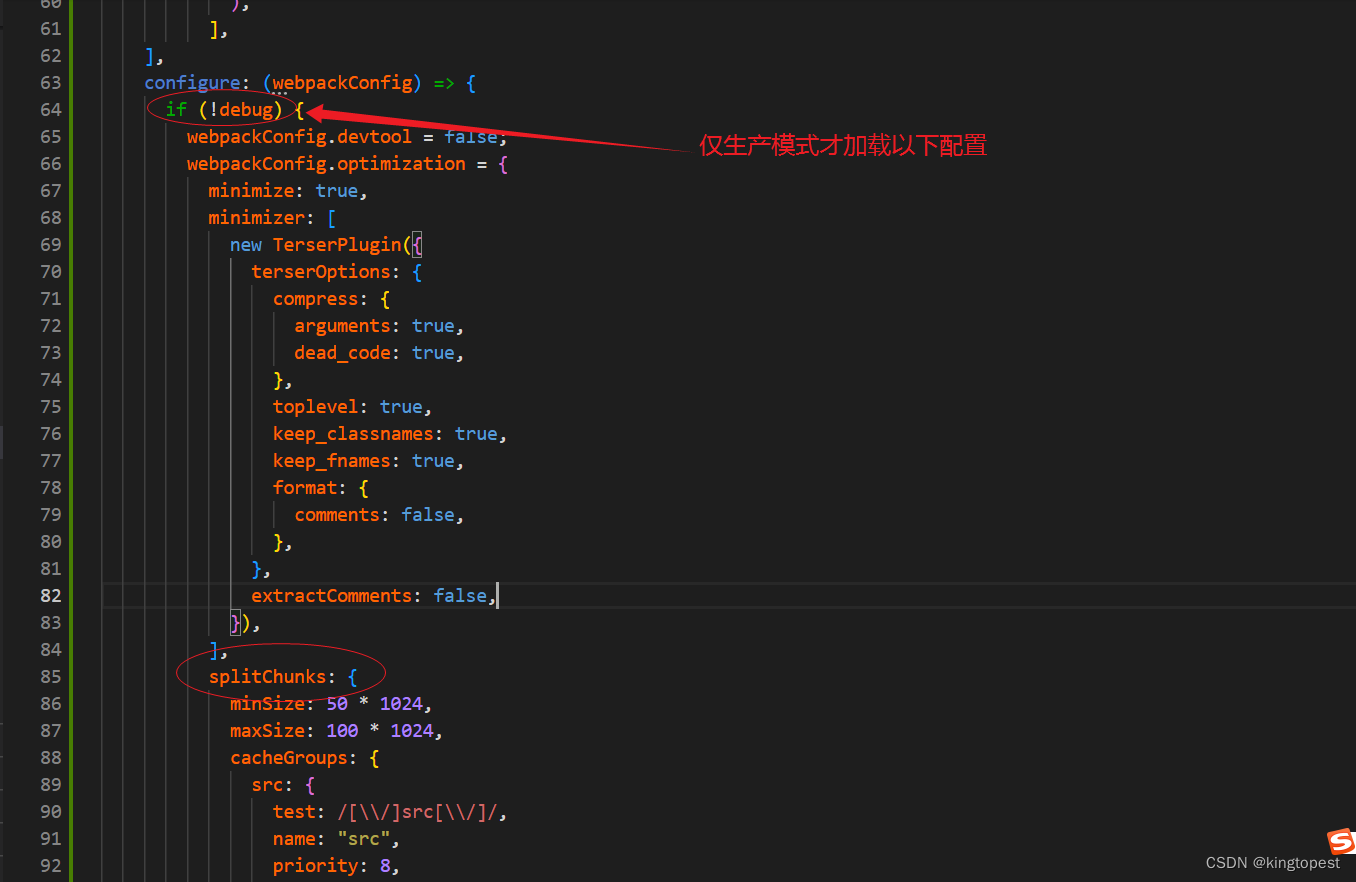
解决craco启动react项目卡死在Starting the development server的问题
现象: 原因:craco.config.ts配置文件有问题 经过排查发现Dev开发模式下不能有splitChunk的配置, 解决办法: 加一个生产模式的判断,开发模式不加载splitChunk的配置,仅在生产模式才加载 判断条件代码&#…...

常见的密码学算法都有哪些?
密码学算法是用于保护信息安全的数学方法和技术。它们可以分为多个类别,包括对称加密、非对称加密、哈希函数和数字签名等。以下是一些常见的密码学算法: 1、对称加密算法: AES(高级加密标准):一种广泛使…...
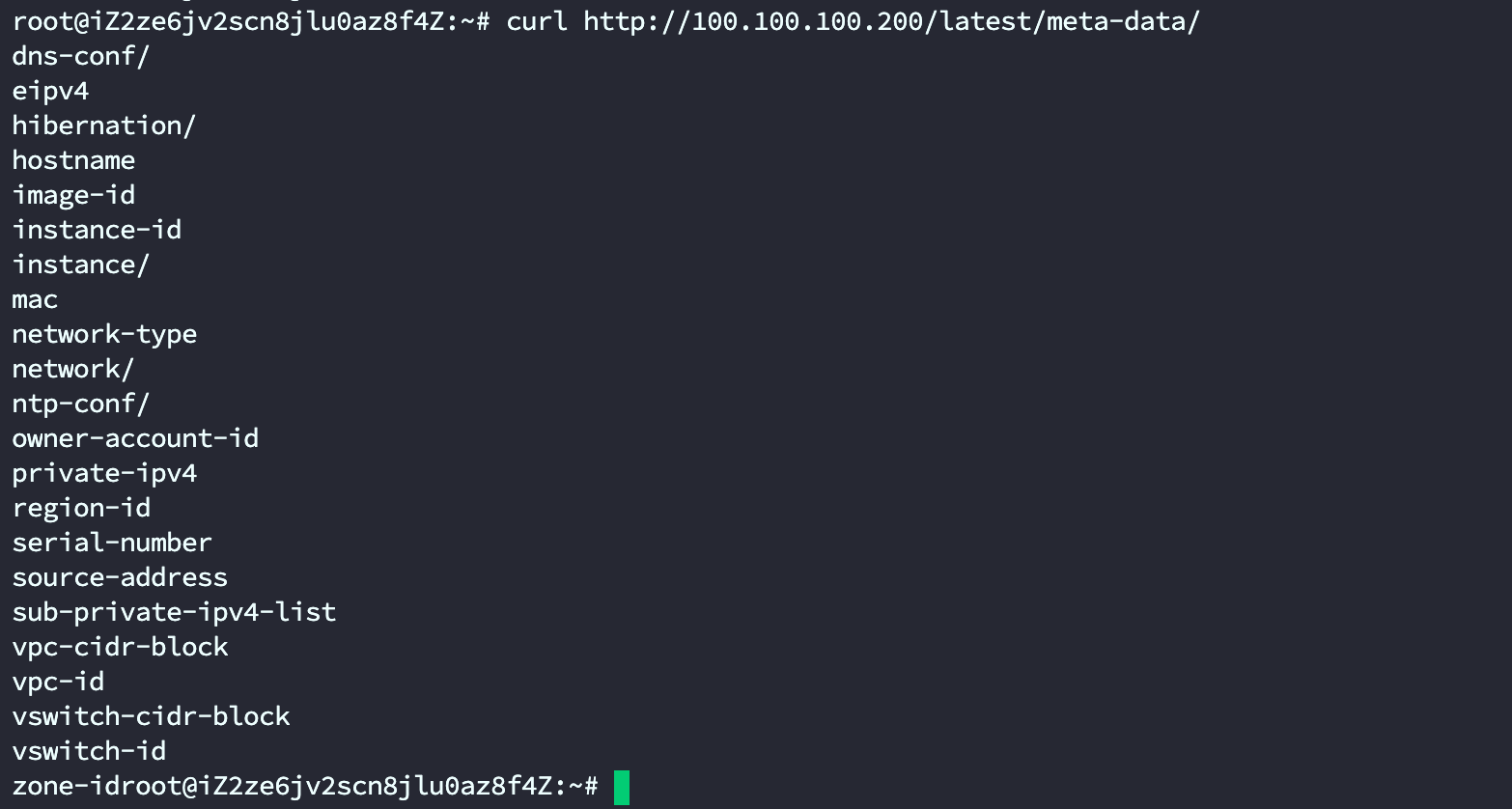
云安全【阿里云ECS攻防】
关于VPC的概念还请看:记录一下弹性计算云服务的一些词汇概念 - 火线 Zone-安全攻防社区 一、初始化访问 1、元数据 1.1、SSRF导致读取元数据 如果管理员给ECS配置了RAM角色,那么就可以获得临时凭证 如果配置RAM角色 在获取ram临时凭证的时候ÿ…...

TBSS数据分析
tbss分析基本流程: 步骤一,指标解算:求解出FA,MD,AD,RD指标 #!/bin/bash #基于体素的形态学分析VBA path/media/kui/Passport5T/DATA_help/TBSS/row_data mkdir ${path}/Results_DTI_tbss mkdir ${path}/R…...

【单调队列】 239. 滑动窗口最大值
239. 滑动窗口最大值 解题思路 计算每一个滑动窗口的最大值 关键在于借助单调队列实现窗口对于单调队列 尾部添加元素 头部删除元素添加元素操作:从尾部开始循环对比 删除比当前元素小的元素获取最大值元素 直接获取头部元素删除元素操作 直接删除头部元素 class…...

Spring实例化源码解析之ComponentScanAnnotationParser(四)
上一章我们分析了ConfigurationClassParser,配置类的解析源码分析。在ComponentScans和ComponentScan注解修饰的候选配置类的解析过程中,我们需要深入的了解一下ComponentScanAnnotationParser的parse执行流程,SpringBoot启动类为什么这么写&…...
约束的作用和使用)
MySQL - 外键(foreign key)约束的作用和使用
什么是外键约束? 外键:用来让两张表的数据之间建立连接,从而保证数据的一致性和完整性。 外键约束是用于建立两个表之间关系的一种约束,它定义了一个表中的列与另一个表中的列之间的关系。外键约束可以保证数据的完整性和一致性…...

前端开发之服务器的基本概念与初识Ajax
1,服务器的基本概念与初识Ajax 1.1 URL地址的组成部分 1.2 客户端与服务器的通信过程 1.3 网页中如何请求数据 1.4 $.get()函数 1.4.1 $.get()函数的语法 // jQuery 中 $.get() 函数的功能单一,专门用来发起 get 请求,从而将服务器上的资源…...

数据结构排序算法---八大排序复杂度及代码实现
文章目录 一、冒泡排序代码实现 二、直接插入排序代码实现 三、希尔排序代码实现 四、选择排序代码实现 五、堆排序代码实现 六、快速排序代码实现 七、归并排序代码实现 八、计数排序代码实现 稳定性:相同的数据排序后,相对位置是否发生改变 一、冒泡排…...

GMS之Launcher中去除默认Search或替换为Chrome Search
将Launcher中搜索框去除 将FeatureFlags.java文件中的QSB_ON_FIRST_SCREEN变量修改为false \system\vendor\mediatek\proprietary\packages\apps\Launcher3\src\com\android\launcher3\config\FeatureFlags.java/*** Defines a set of flags used to control various launche…...
@DateTimeFormat 和 @JsonFormat 的详细研究
关于这两个时间转化注解,先说结论 一、介绍 1、DateTimeFormat DateTimeFormat 并不会根据得到其属性 pattern 把前端传入的数据转换成自己想要的格式,而是将前端的String类型数据封装到Date类型;其次它的 pattern 属性是用来规范前端传入…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...
