数据结构排序算法---八大排序复杂度及代码实现
文章目录
- 一、冒泡排序
- 代码实现
- 二、直接插入排序
- 代码实现
- 三、希尔排序
- 代码实现
- 四、选择排序
- 代码实现
- 五、堆排序
- 代码实现
- 六、快速排序
- 代码实现
- 七、归并排序
- 代码实现
- 八、计数排序
- 代码实现
稳定性:相同的数据排序后,相对位置是否发生改变
一、冒泡排序
时间复杂度:O(N^2)
空间复杂度:O(1)
稳定性:稳定
代码实现
void Swap(int* a, int* b)
{int tmp;tmp = *a;*a = *b;*b = tmp;
}
void BubbleSort(int* a, int n)
{for (int j = 0; j < n; j++){int exchange = 0;for (size_t i = 1; i < n-j; i++)if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}if (exchange == 0){break;}}
}
二、直接插入排序
时间复杂度:O(N^2)
空间复杂度:O(1)
稳定性:稳定
代码实现
void InsertSort(int* a, int n)
{for (int i = 0; i < n; i++){int end = i;int tmp = a[end + 1];while (end>=0){if (tmp < a[end])a[end + 1] = a[end];elsebreak;--end;}a[end + 1] = tmp;}
}
三、希尔排序
时间复杂度:O(N^1.3)
空间复杂度:O(1)
稳定性:不稳定
代码实现
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}elsebreak;}a[end + gap] = tmp;}}
}
四、选择排序
时间复杂度:O(N^2)
空间复杂度:O(1)
稳定性:不稳定
代码实现
void SelectSort(int* a, int n)
{int begin = 0;int end = n - 1;while (begin < end){int max = begin, min = begin;for (int i = begin+1; i <= end; i++){if (a[i] > a[max])max = i;if (a[i] < a[min])min = i;}Swap(&a[begin], &a[min]);if (max == begin)max = min;Swap(&a[end], &a[max]);--end;++begin;}
}
五、堆排序
时间复杂度:O(N*logN)
空间复杂度:O(1)
稳定性:不稳定
代码实现
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapSort(int* a, int n)
{for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}
六、快速排序
时间复杂度:O(N*logN)
空间复杂度:O(logN)
稳定性:不稳定
代码实现
//三数取中
int GetMidi(int* a, int left, int right)
{int midi = (left + right) / 2;if (a[left] < a[midi]){if (a[midi] < a[right])return midi;else if (a[right] < a[left])return left;elsereturn right;}else{if (a[left] < a[right])return left;else if (a[right] < a[midi])return midi;elsereturn right;}
}
//hoare
int PartSort1(int* a, int left,int right)
{int keyP = left;//GetMidi(a,left,right);while (left < right){while (a[right] >= a[keyP] && left < right)--right;while (a[left] <= a[keyP] && left < right)++left;Swap(&a[left], &a[right]);}Swap(&a[keyP], &a[left]);return left;
}
//挖坑法
int PartSort2(int* a, int left, int right)
{int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int keyP = a[left];//int keyP = left;int hole = left;while (left < right){while (a[right] >= keyP && left < right)--right;a[hole] = a[right];hole = right;while (a[left] <= keyP && left < right)++left;a[hole] = a[left];hole = left;}a[hole] = keyP;return hole;
}
//前后指针
int PartSort3(int* a, int left, int right)
{int prev = left;int cur = prev + 1;int keyP = left;while (cur <= right){if (a[cur] < a[keyP] && ++prev != cur){Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[prev], &a[keyP]);return prev;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int key = PartSort1(a, begin, end);QuickSort(a, begin, key - 1);QuickSort(a, key + 1, end);
}void QuickSort1(int* a, int begin, int end)
{if (begin >= end)return;//小区间优化,小区间不在递归分割排序,降低递归次数if ((end - begin + 1) > 10){int key = PartSort1(a, begin, end);QuickSort1(a, begin, key - 1);QuickSort1(a, key + 1, end);}else{InsertSort(a + begin, end - begin + 1);}
}void QuickSortNonR(int* a, int begin, int end)//非递归
{Stack st;StackInit(&st);StackPush(&st, end);StackPush(&st, begin);while (!StackEmpty(&st)){int left = StackTop(&st);StackPop(&st);int right = StackTop(&st);StackPop(&st);int key = PartSort3(a, left, right);if (key + 1 < right){StackPush(&st, right);StackPush(&st, key + 1);}if (begin < key - 1){StackPush(&st, key - 1);StackPush(&st, begin);}}StackDestory(&st);
}
其中包含了,三数取中(基准值),快排的三种实现方法(hoare,挖坑法,前后指针)及非递归方法
七、归并排序
时间复杂度:O(N*logN)
空间复杂度:O(N)
稳定性:稳定
代码实现
void PartMergeSort(int* a, int* tmp, int begin, int end)
{if (end <= begin)return;int mid = (begin + end) / 2;PartMergeSort(a, tmp, begin, mid);PartMergeSort(a, tmp, mid + 1, end);int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int count = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2])tmp[count++] = a[begin1++];elsetmp[count++] = a[begin2++];}while (begin1 <= end1){tmp[count++] = a[begin1++];}while (begin2 <= end2){tmp[count++] = a[begin2++];}memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}void MergeSort(int* a, int n)
{int* tmp = malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");exit(-1);}PartMergeSort(a, tmp, 0, n - 1);free(tmp);
}void MergeSortNonR(int* a, int n)
{int* tmp = malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");exit(-1);}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;int count = i;if (begin2 >= n)break;if (end2 >= n)end2 = n - 1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2])tmp[count++] = a[begin1++];elsetmp[count++] = a[begin2++];}while (begin1 <= end1){tmp[count++] = a[begin1++];}while (begin2 <= end2){tmp[count++] = a[begin2++];}memcpy(a + i, tmp + i, (end2-i+1) * sizeof(int));} gap *= 2;}
}
其中包含了递归及非递归实现方法
八、计数排序
时间复杂度:O(N+range)
空间复杂度:O(range)
代码实现
void CountSort(int* a, int n)
{int min = a[0], max = a[0];for (size_t i = 0; i < n; i++){if (a[i] < min)min = a[i];if (a[i] > max)max = a[i];}int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);printf("\nrange:%d\n", range);if (count == NULL){perror("malloc fail");return;}memset(count, 0, sizeof(int) * range);// 统计数据出现次数for (int i = 0; i < n; i++){count[a[i] - min]++;}// 排序int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}
}
相关文章:

数据结构排序算法---八大排序复杂度及代码实现
文章目录 一、冒泡排序代码实现 二、直接插入排序代码实现 三、希尔排序代码实现 四、选择排序代码实现 五、堆排序代码实现 六、快速排序代码实现 七、归并排序代码实现 八、计数排序代码实现 稳定性:相同的数据排序后,相对位置是否发生改变 一、冒泡排…...

GMS之Launcher中去除默认Search或替换为Chrome Search
将Launcher中搜索框去除 将FeatureFlags.java文件中的QSB_ON_FIRST_SCREEN变量修改为false \system\vendor\mediatek\proprietary\packages\apps\Launcher3\src\com\android\launcher3\config\FeatureFlags.java/*** Defines a set of flags used to control various launche…...
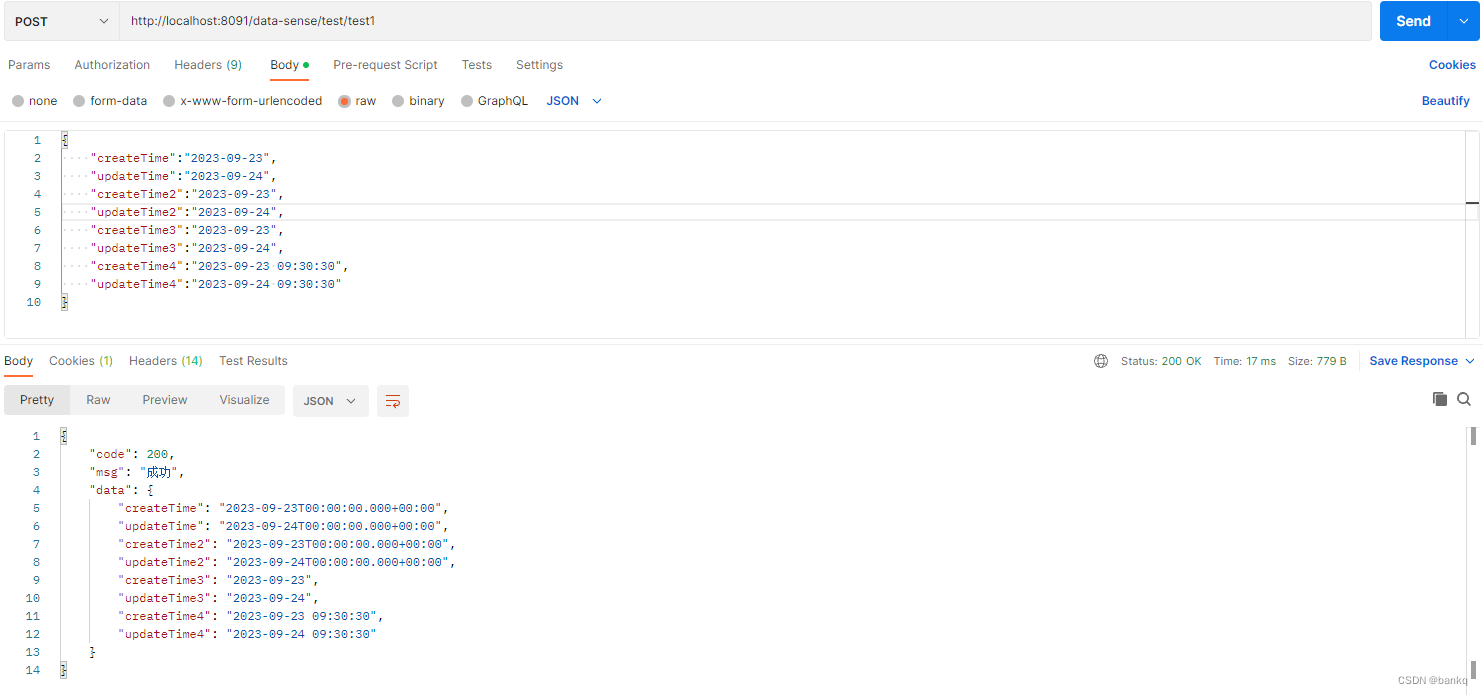
@DateTimeFormat 和 @JsonFormat 的详细研究
关于这两个时间转化注解,先说结论 一、介绍 1、DateTimeFormat DateTimeFormat 并不会根据得到其属性 pattern 把前端传入的数据转换成自己想要的格式,而是将前端的String类型数据封装到Date类型;其次它的 pattern 属性是用来规范前端传入…...
nodejs基于Vue.js健身体育器材用品商城购物网97794
管理员端的功能主要是开放给系统的管理人员使用,能够对用户的信息进行管理,包括对用户、健身器材、器材类型、系统和订单进行查看,修改和删除、新增等,对系统整体运行情况进行了解。用户的功能主要是对个人账号和密码进行更新信息…...

C#WPF框架Microsoft.Toolkit.MvvM应用实例
本文实例演示C#WPF框架Microsoft.Toolkit.MvvM应用 目录 一、MVVM概述 二、MVVMLight概述 三、使用Microsoft.Toolkit.Mvvm框架 一、MVVM概述 MVVM概述MVVM是Model-View-ViewModel的简写,主要目的是为了解耦视图(View)和模型(Model)。...

蓝桥杯每日一题2023.9.27
4408. 李白打酒加强版 - AcWing题库 题目描述 题目分析 对于这题我们发现有三个变量,店,花,酒的数量,对于这种范围我们使用DP来进行分析。 dp[i][j][k]我们表示有i个店,j朵花,k单位酒的集合,…...
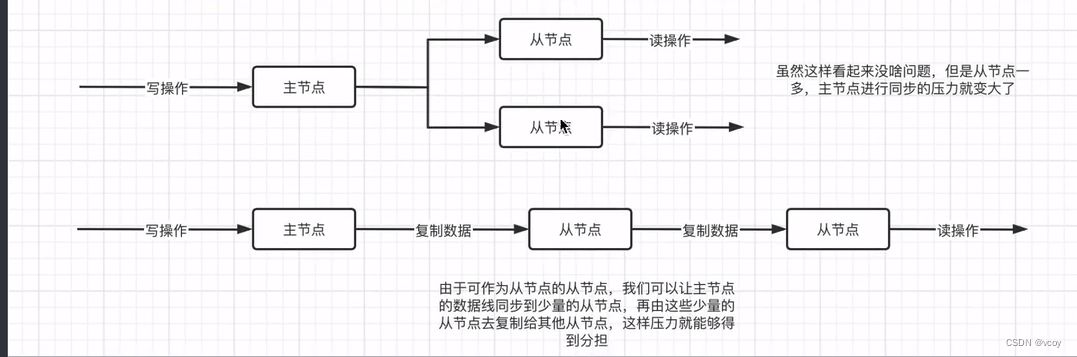
Redis与分布式-主从复制
接上文 常用中间件-OAuth2 1.主从复制 启动两个redis服务器。 修改第一个服务器地址 修改第二个redis 然后分别启动 redis-server.exe redis.windows.conf) 查看当前服务器的主从状态,打开客户端:输入info replication命令来查看当前的主从状态&am…...
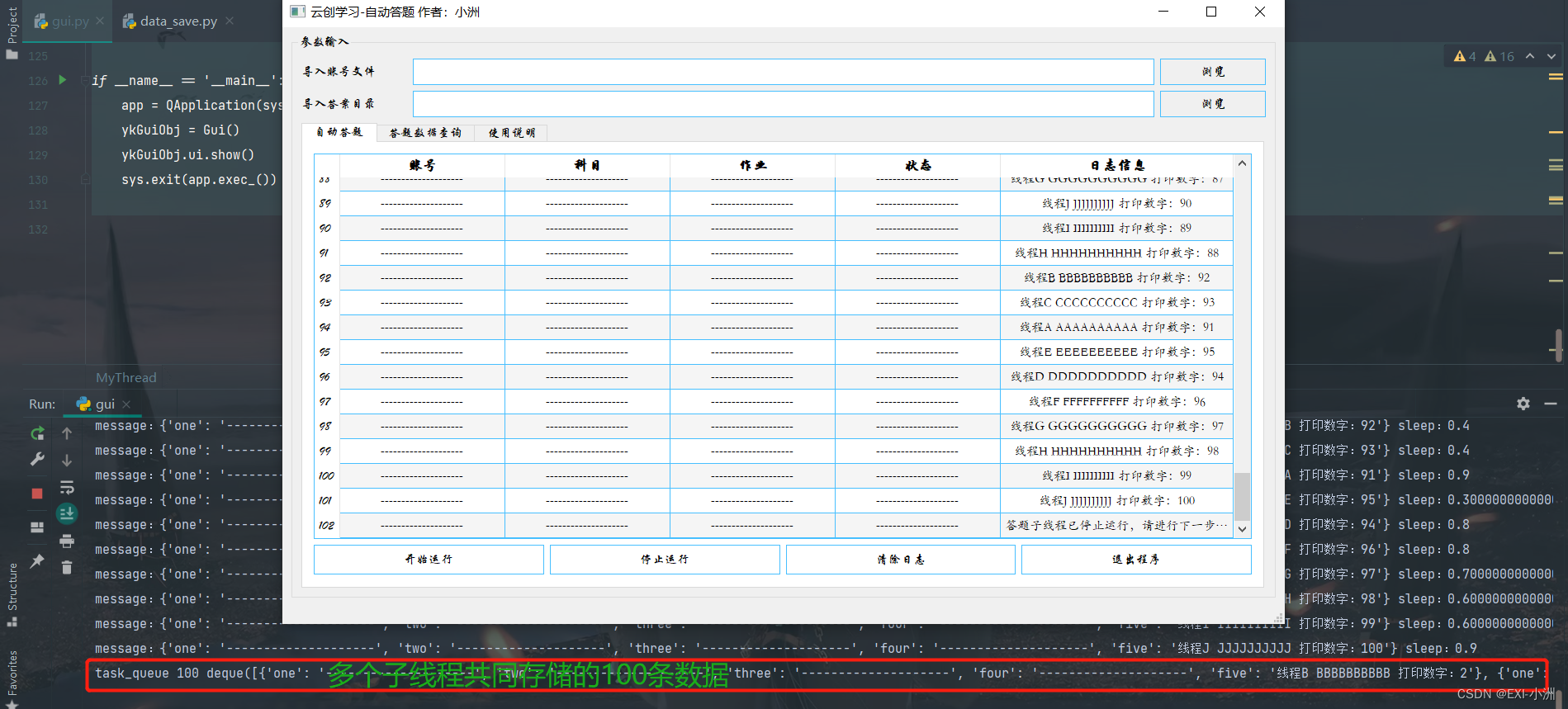
QT pyside2 线程嵌套子线程 实现开始运行和停止运行
文章目录 前言为什么要使用多线程 一、单个线程实现按钮方法的执行二、线程嵌套多个子线程实现按钮方法的执行三、QT GUI常用代码3.1 多线程取出队列任务循环执行,无停止3.2 将某个方法放在线程中执行3.3 QT pyside2 tableWidget 清除日志3.4 退出整个GUI程序(杀死进…...

江西广电会展集团总经理李悦一行莅临拓世科技集团调研参观,科技璀璨AIGC掀新潮
在江西这片充满活力的土地上,数字经济如潮水般涌动,会展文化与科技的完美结合,正如新时代的璀璨繁星照亮夜空,更预示着一场AIGC创新的壮丽篇章即将展开。作为拓世科技集团的老朋友,江西广电多位领导多次莅临拓世科技集…...

【RabbitMQ实战】06 RabbitMQ配置
一、概述 一般情况下,可以使用默认的内建配置来有效地运行RabbitMQ,并且大多数情况下也并不需要修改任何 RabbitMQ的配置。当然,为了更加有效地操控 RabbitMQ,也可以利用调节系统范围内的参数来达到定制化的需求。 RabbitMQ提供…...
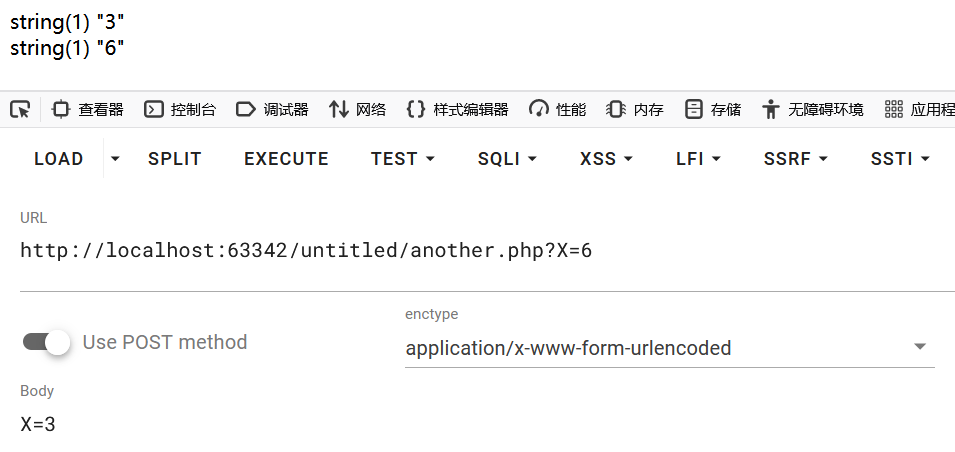
CTF 全讲解:[SWPUCTF 2021 新生赛]jicao
文章目录 参考环境题目index.phphighlight_file()include()多次调用,多次执行单次调用,单次执行 $_POST超全局变量HackBarHackBar 插件的获取 $_POST打开 HackBar 插件通过 HackBar 插件发起 POST 请求 GET 请求查询字符串超全局变量 $_GET JSONJSON 数据…...
FL Studio21.1电脑试用体验版音乐制作软件
我一直以来对音乐艺术都很感兴趣。最近我接触到了一款名为 FL Studio 的电脑版音乐制作软件,深感其强大功能和广泛适用性。通过使用这款软件,我不仅深入了解了音乐制作的过程与技巧,也加深了对音乐创作的理解。 FL Studio 最初是一款针对 MI…...
)
【数据结构】单链表的基本操作(节点建立、插入删除)
1. 单链表的基本操作 1.1. 链表的定义1.2. 链表的创建(初始化) 1.2.1. 不带头结点的链表1.2.2. 带头结点的链表 1.3. 链表的插入和删除 1.3.1. 按位序插入 1.3.1.1. 带头结点1.3.1.2. 不带头结点 1.3.2. 指定节点的后插操作1.3.3. 指定元素的前插操作1.3…...
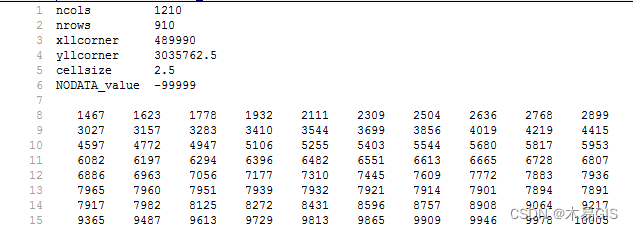
DEM格式转换:转换NSDTF-DEM国标数据格式为通用格式,使用ArcGIS工具转换NSDTF-DEM国标.dem文件为通用.tif格式。
DEM格式转换:转换NSDTF-DEM国标数据格式为通用格式,使用ArcGIS工具转换NSDTF-DEM国标.dem文件为通用.tif格式。 *.dem是一种比较常见的DEM数据格式,其有两种文件组织方式,即NSDTF-DEM和USGS-DEM。 (1)NSDT…...

施耐德电气:勾勒未来工业愿景,赋能中国市场
9月19日,第23届中国国际工业博览会(简称“工博会”)在上海隆重召开。作为全球能源管理和自动化领域的数字化转型专家,施耐德电气在工博会现场全方位展现了自身对未来工业的全新视野与深刻见解,不仅展示了其贯通企业设计…...
安防监控产品经营商城小程序的作用是什么
安防监控产品覆盖面较大,监控器、门禁、对讲机、烟感等都有很高用途,家庭、办公单位各场景往往用量不少,对商家来说,市场高需求背景下也带来了众多生意,但线下门店的局限性,导致商家想要进一步增长不容易。…...

php中判断指定字符串是否包含指定字符的封装函数
在 PHP 中,你可以使用内置的字符串函数 strpos() 来判断一个字符串是否包含指定的字符或子字符串。以下是一个简单的封装函数,它使用 strpos() 来判断指定字符串是否包含指定字符,并返回一个布尔值。 function stringContains($string, $cha…...
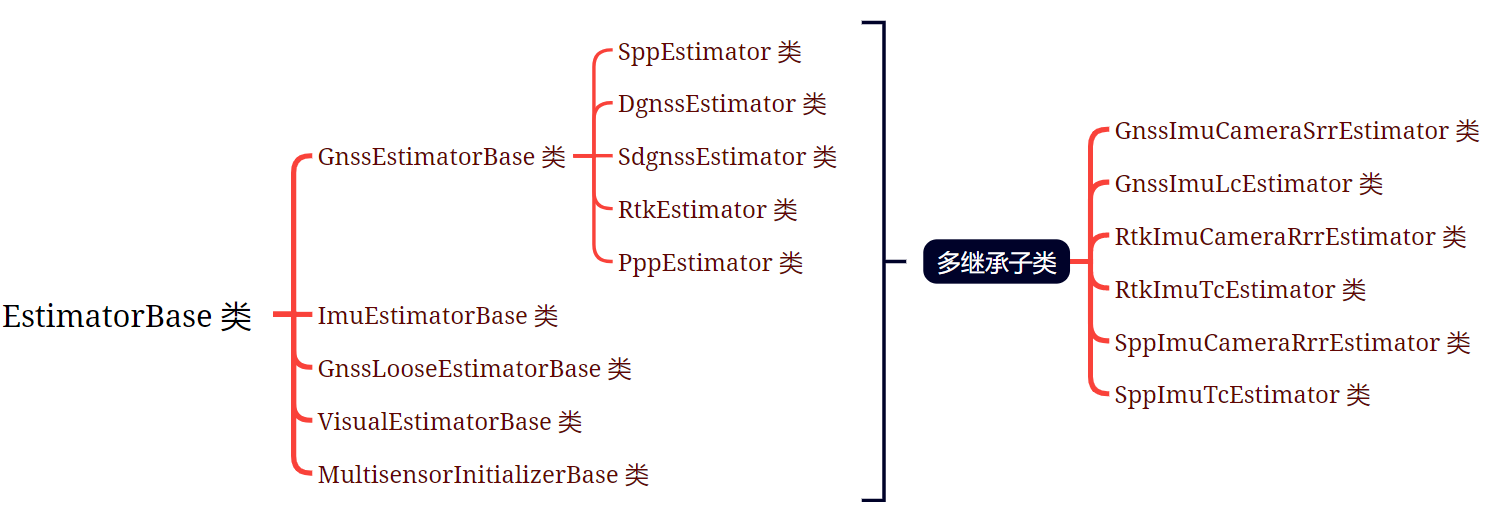
GICI-LIB源码阅读(三)因子图优化模型
原始 Markdown文档、Visio流程图、XMind思维导图见:https://github.com/LiZhengXiao99/Navigation-Learning 文章目录 三、因子图优化(FGO)1、因子图模型2、因子图优化状态估计模型3、因子图优化求解4、Ceres 非线性最小二乘库5、GICI-LIB 中…...
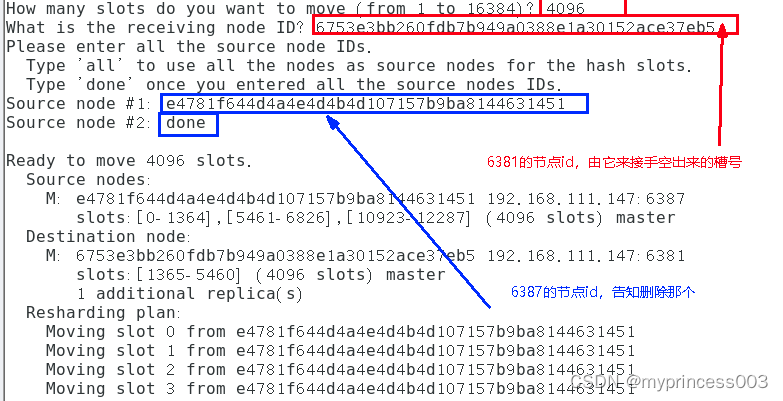
5、Docker安装mysql主从复制与redis集群
安装mysql主从复制 主从搭建步骤 1.1 新建主服务器容器实例3307 docker run -p 3307:3306 --name mysql-master #3307映射到3306,容器名为mysql-master -v /app/mysql/mydata/mysql-master/log:/var/log/mysql #容器数据卷 -v /app/mysql/mydata/mysql-master/dat…...

【AI视野·今日NLP 自然语言处理论文速览 第四十三期】Thu, 28 Sep 2023
AI视野今日CS.NLP 自然语言处理论文速览 Thu, 28 Sep 2023 Totally 38 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers Cross-Modal Multi-Tasking for Speech-to-Text Translation via Hard Parameter Sharing Authors Brian Yan,…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...
