前端判断: []+[], []+{}, {}+[], {}+{}
本质: 二元操作符+规则
一般判断规则:
- 如果操作数是对象,则对象会转换为原始值
- 如果其中一个操作数是字符串的话,另一个操作数也会转换成字符串,进行字符串拼接
- 否则,两个操作数都将转换成数字或NaN,进行加法操作
转为原始数据类型的值的方法:
- Symbol.ToPrimitive
- Object.prototype.valueOf
- Object.prototype.toString
一. []的原值
- typeof [][Symbol.ToPrimitive] // undefined
- [].valueOf() // []
- [].toString() // ‘’
所以[] + [] 就相当于 ''+'', 得到的是空字符串''
二.{}的原始值
- typeof {}[Symbol.ToPrimitive] // undefined
- ({}).valueOf() // {}
- ({}).toString() // '[object Object]'
注意事项: {}+xx需要看成{};+xx才是得到和控制台一样的值
比如:
({} + []) 相当于是'[object Object]' + '', 得到的是'[object Object]'
{} + [] 相当于{}; + [], 分号说明语句结束了,所以要往后看,而+号本身有隐式转换数字的功能, 所以+[]等于0
同理:
({} + {})是'[object Object][object Object]'
而{} + {}相当于{}; + {},相当于只需要看+{}, {}的原始值是'[object Object]',隐式转换'[object Object]'为数字,'[object Object]'无法转换为正常数字,所以变成NaN
因此:
[] + ???就相当于([] + ???)
而{}的+运算特殊一些:
{} + ??? 相当于 +???转换为数字, 得到0或者NaN
({} + ???) 相当于分别得到{}的原始值和???的原始值, 即('[object Object]' +???的原始值)
综上所述:
[]+[] =>得到 ''
[]+{} =>得到 '[object Object]'
{} + [] =>得到 0
{} + {} => 得到NaN
相关文章:

前端判断: []+[], []+{}, {}+[], {}+{}
本质: 二元操作符规则 一般判断规则: 如果操作数是对象,则对象会转换为原始值如果其中一个操作数是字符串的话,另一个操作数也会转换成字符串,进行字符串拼接否则,两个操作数都将转换成数字或NaN,进行加法操作 转为原始数据类型的值的方法: Symbol.ToPrimitiveObject.protot…...
)
el-input-number/el-input 实现实时输入数字转换千分位(失焦时展示千分位)
el-input-number/el-input 实现实时输入数字转换千分位(失焦时展示千分位) 我把封装指令的代码放在了main.js,代码如下 // 金额展示千分位 Vue.directive("thousands", {inserted: function(el, binding) {// debugger// 获取input节点if (el.tagName.toLocaleUppe…...

一篇博客学会系列(2)—— C语言中的自定义类型 :结构体、位段、枚举、联合体
目录 前言 1、结构体 1.1、结构体类型的声明 1.2、特殊的结构体类型声明 1.3、结构体的自引用 1.4、结构体的定义和初始化 1.5、结构体成员变量的调用 1.6、结构体内存对齐 1.6.1、offsetof 1.6.2、结构体大小的计算 1.6.3、为什么存在内存对齐? 1.7、…...
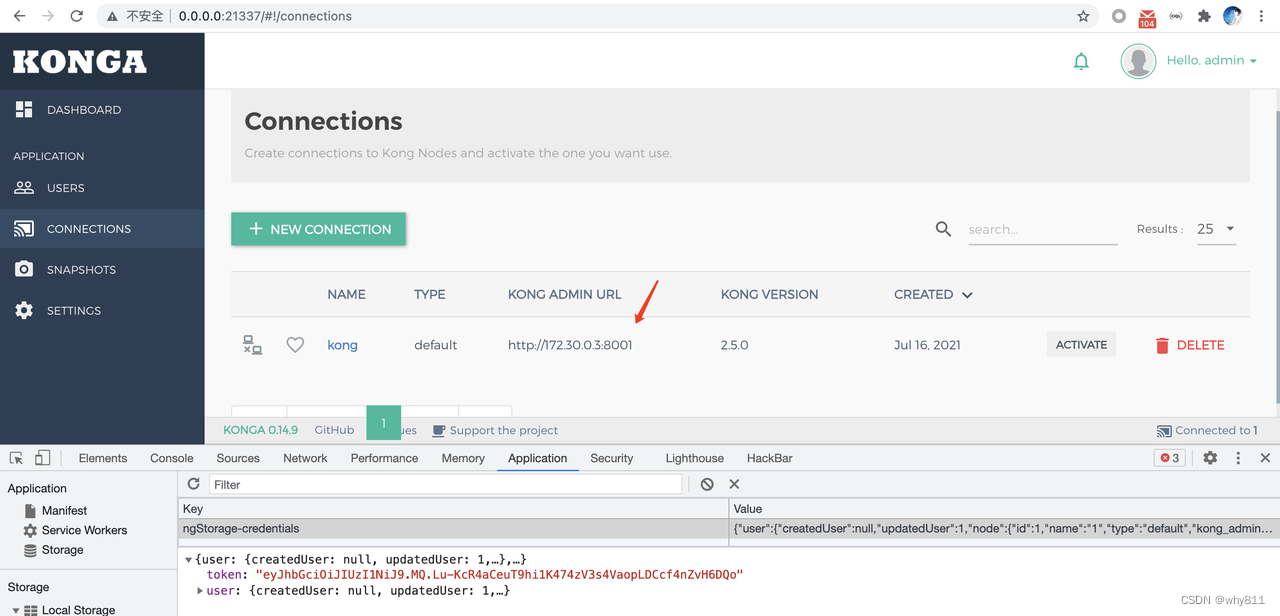
KongA 任意用户登录漏洞分析
KongA 简介 KongA 介绍 KongA 是 Kong 的一个 GUI 工具。GitHub 地址是 https://github.com/pantsel/konga 。 KongA 概述 KongA 带来的一个最大的便利就是可以很好地通过UI观察到现在 Kong 的所有的配置,并且可以对于管理 Kong 节点 漏洞成因 未设置TOKEN_SECRE…...
吉力宝:智能科技鞋品牌步力宝引领传统产业创新思维
在现代经济环境下,市场经济下产品的竞争非常的激烈,如果没有营销,产品很可能不被大众认可,酒香也怕巷子深,许多传统产业不得不面临前所未有的挑战。而为了冲出这个“巷子”,许多企业需要采用创新思维&#…...
)
【IPC 通信】信号处理接口 Signal API(1)
收发信号思想是 Linux 程序设计特性之一,一个信号可以认为是一种软中断,通过用来向进程通知异步事件。 本文讲述的 信号处理内容源自 Linux man。本文主要对各 API 进行详细介绍,从而更好的理解信号编程。 信号概述 遵循 POSIX.1,…...
使用GDIView排查GDI对象泄漏导致的程序UI界面绘制异常问题
目录 1、问题说明 2、初步分析 3、查看任务管理器,并使用GDIView工具分析 4、GDIView可能对Win10兼容性不好,显示的GDI对象个数不太准确 5、采用历史版本比对法,确定初次出现问题的时间点,并查看前一天的代码修改记录 6、将…...

蓝桥等考Python组别一级001
第一部分:选择题 1、Python L1 (15分) 下面哪个不是Python的编程环境?( ) Python在线编程IDLEPyCharmScratch正确答案:D 2、Python L1(15分) 世界上第一台通用电子计算机ENIAC是在( )诞生的。 美国英国日本德国正确答案:A 3、Python L1(20分) 关于P…...

Unity之Hololens2开发 如何接入的MRTK OpenXR Plugin
一.前言 什么是Hololens? Hololens是由微软开发的一款混合现实头戴式设备,它将虚拟内容与现实世界相结合,为用户提供了沉浸式的AR体验。Hololens通过内置的传感器和摄像头,能够感知用户的环境,并在用户的视野中显示虚拟对象。这使得用户可以与虚拟内容进行互动,将数字信…...
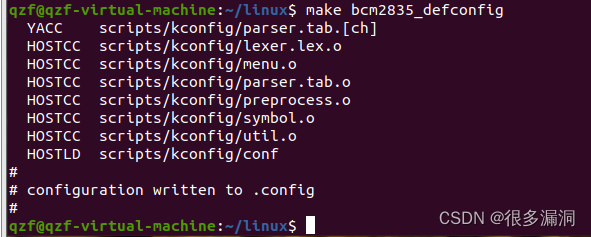
Ubuntu系统Linux内核安装和使用
安装: 检查树莓派Linux版本,我的是6.1 uname -r 内核下载链接: Raspberry Pi GitHub 找对应版本下载 导入之后,解压安装即可 unzip linux-rpi-6.1.y.zip 其他内容 treee 指令安装 sudo apt-get install tree 使用这…...
”)
数学术语之源——群同态的“核(kernel)”
1. “kernel”这个术语在群论中的起源 Ivar Fredholm 在 1903 年的第27期Acta Math 数学学报发表的一篇关于“积分方程(INTEGRAL EQUATIONS)”的著名论文(“关于一类函数方程(Sur une classe des quations fonctionnelles)”)中使用了法语“noyau(核)”(365-390页)。 David …...
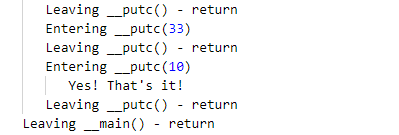
defcon-quals 2023 crackme.tscript.dso wp
将dso文件放到data/ExampleModule目录下,编辑ExampleModule.tscript文件 function ExampleModule::onCreate(%this) { trace(true); exec("./crackme"); __main("aaaaaaaa"); quit(); } 然后点击主目录下的Torque3D-debug.bat就可以在生成的c…...

前端开发 vs. 后端开发:编程之路的选择
文章目录 前端开发:用户界面的创造者1. HTML/CSS/JavaScript:2. 用户体验设计:3. 响应式设计:4. 前端框架: 后端开发:数据和逻辑的构建者1. 服务器端编程:2. 数据库:3. 安全性&#…...

算法练习4——删除有序数组中的重复项 II
LeetCode 80 删除有序数组中的重复项 II 给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。 不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 …...
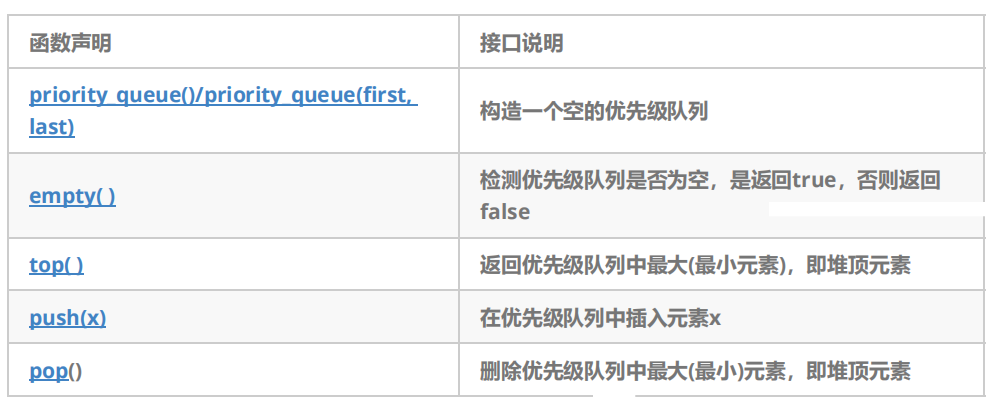
【C++进阶(六)】STL大法--栈和队列深度剖析优先级队列适配器原理
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:C从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习C 🔝🔝 栈和队列 1. 前言2. 栈和队列的接口函数熟悉3. …...

linux opensuse使用mtk烧录工具flashtool
环境 linux发行版:opensuse leap 15.5 工具:SP_Flash_Tool_Selector_exe_Linux_v1.2316.00.100.rar 或其他版本 目标:mtk设备 下载链接 https://download.csdn.net/download/zmlovelx/88382784 或网络搜索。 使用 opensuse可直接解压后使…...
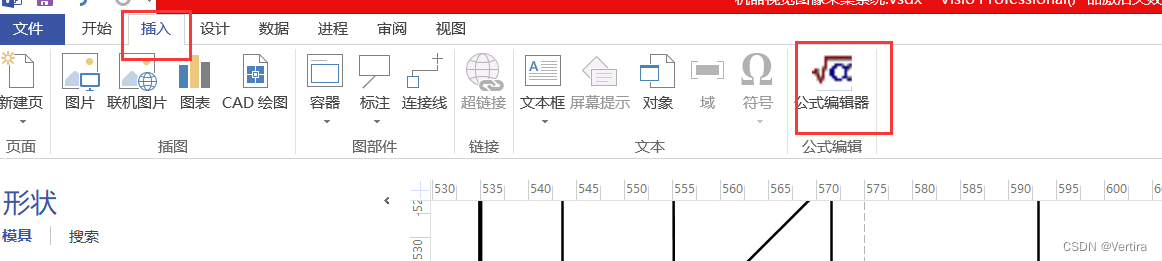
Visio如何对文本打下标、上标,以及插入公式编辑器等问题(已解决)
解决这个问题的本质问题,就是在Visio中插入公式编辑器(这不是visio的常用命令,需要添加)。 打开Visio--》文件--选项 点击选项,弹出对话框。在自定义功能区中,点击 常用命令,在下拉选项中&#…...
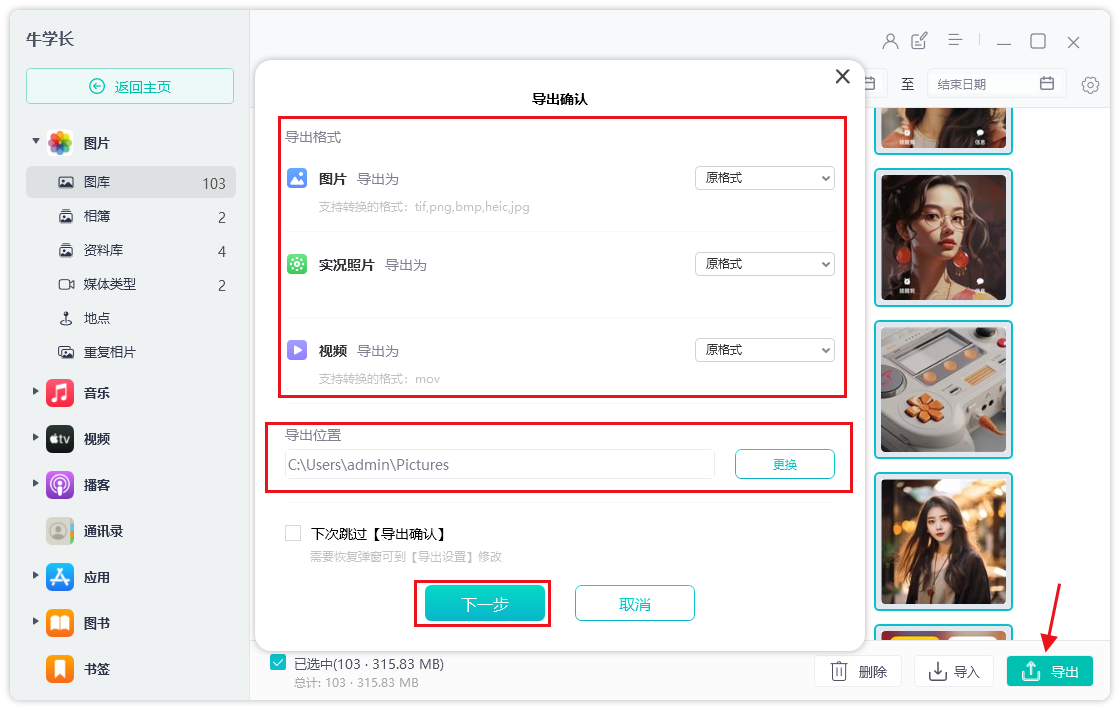
快速将iPhone大量照片快速传输到电脑的办法!
很多使用iPhone 的朋友要将照片传到电脑时,第一时间都只想到用iTunes 或iCloud,但这2个工具真的都非常难用,今天小编分享牛学长苹果数据管理工具的照片传输功能,他可以快速的将iPhone照片传输到电脑上,并且支持最新的i…...

TCP/IP协议簇包含的协议
应用层(Application Layer): HTTP(Hypertext Transfer Protocol):用于Web浏览器和Web服务器之间的通信。HTTPS(Hypertext Transfer Protocol Secure):安全的HTTP版本&…...
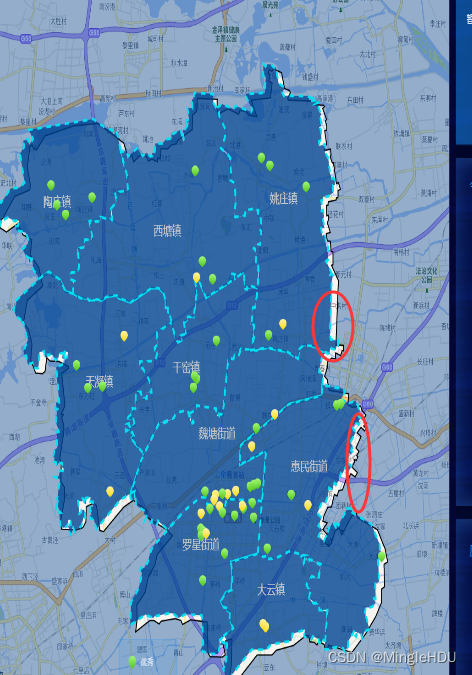
天地图绘制区域图层
背景: 业务方要求将 原效果图 参考效果图 最终实现效果 变更点: 1.将原有的高德地图改为天地图 2.呈现形式修改:加两层遮罩:半透明遮罩层mask区域覆盖物mask 实现过程: 1.更换地图引入源 <link rel"style…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...
