数学术语之源——群同态的“核(kernel)”
1. “kernel”这个术语在群论中的起源
Ivar Fredholm 在 1903 年的第27期Acta Math 数学学报发表的一篇关于“积分方程(INTEGRAL EQUATIONS)”的著名论文(“关于一类函数方程(Sur une classe des équations fonctionnelles)”)中使用了法语“noyau(核)”(365-390页)。
David Hilbert在他的<<线性积分方程一般理论原理>>(Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen)(Nachrichten von d) 中将其翻译成德语,称为“Kern”(Nachrichten von d. Königl. Ges. d. Wissensch. zu Göttingen (Math.-physik. Kl.)(1904年) 第49页)。
在英语中,“kernel”在数学中作为术语最早出现在M. Bôcher的著作<<积分方程研究导论>>(Introduction to the Study of Integral Equations)一书中(1909年),书中将其描述为“K is called the kernel of these equations(称K为这些积分方程的核)”(引自牛津英语词典)。参见 G. Birkhoff 和 E. Kreyszig (1984)“泛函分析的建立”,Historia Mathematica, 11,258-321。
到 A. Zygmund 的三角级数 (1935) 时代,“kernel”已成为Fourier分析中的一个既定术语。通过JSTOR 搜索发现,在 Charles N. Moore 的“On the Application of Borel's Method to the Sumation of Fourier's Series”中发现了“Fejér 核”和“Dirichlet 核”(Proceedings of the National Academy, 11, (1925), 284-287),但这不太可能是这些术语的首次公开使用。
“kernel”使用Fourier理论进入统计学,描述谱密度和概率密度函数的估计。 JSTOR 搜索发现,E. F. Schuster(数学统计年鉴,40,(1969年),第 1187 页)指的是“所谓的核估计类”,由 M. Rosenblatt 在“关于密度函数的一些非参数估计的评述”中引入的(Annals of Mathematical Statistics,27,(1956年),第832-837页)。早期的“Fejér kernel”曾用于 U. Grenander 和 M.Rosenblatt 的“平稳随机过程产生的时间序列的统计谱分析(Statistical Spectral Analysis of Time Series Arising from Stationary Stochastic Processes)”,Annals of Mathematical Statistics,24,(1953年),第537-558页。另一个在时间序列分析中特别流行的术语是“window”。另见“Fejér kernel”。
“kernel”在代数中的使用似乎与其在积分方程和Fourier分析中的使用无关。 L. Pontrjagin 于 1931 年在《数学》杂志的论文“Über den algebraischen Inhalt topologischer Dualitätssätze”的第 102 页上使用了该术语。年鉴 105。《牛津英语词典》引用了Pontrjagin的<<拓扑群 i.11>>( Topological Groups)中的以下内容(由 E. Lehmer 1946年翻译)“在同态 g 下被映射到群 G* 的玄元上的群 G 的所有元素的集合称为该同态的核。”
G. D. Birkhoff 和 S. A. MacLane <<现代代数综述>>( A Survey of Modern Algebra)第 3 版 1965 年,第 213-214 页将同态和核的概念应用于被视为加法下Abel群的向量空间之间的线性变换 T 。 他们评论说:“由于 O 是群的玄元,因此 T 的零空间正是被视为群同态的 T 的核。” 请参阅条目 NULL SPACE。
2. “kernel”这个术语在群论中的含义
从上面第1点可以看出,“kernel”这个术语在数学的多个分支都有使用,至少在积分方程、Fourier分析、群论中都有作为术语使用。但就这个术语的确切含义,只有放到具体的数学分支中的知识点上才能说明。或许,当初引入这个术语的作者认为这个特征比较核心,因此用这个词描述。比如在Fourier分析中,“核”指的是在某个范围内的积分恒为1。
关于核在代数群论中的含义,引用Michael Artin 在他的书中的说明,或许能导出“核”在群论中的含义。书中说,“核非常重要,原因在于它控制着整个同态。它不仅告知了我们G 中的哪些元素被映射到G’的幺元,而且还告知了我们G中的哪些元素对在G’中具有相同的像。” 这或许就是当初群论中引入术语“核”来描述这一数学现象的原因。
参考资料:
1. Earliest Known Uses of Some of the Words of Mathematics (K)
Earliest Known Uses of Some of the Words of Mathematics (K)
更多术语:
https://web.archive.org/web/20170612233228/http://jeff560.tripod.com/mathsym.html
2. <<Algebra>> Michael Artin, 2th
相关文章:
”)
数学术语之源——群同态的“核(kernel)”
1. “kernel”这个术语在群论中的起源 Ivar Fredholm 在 1903 年的第27期Acta Math 数学学报发表的一篇关于“积分方程(INTEGRAL EQUATIONS)”的著名论文(“关于一类函数方程(Sur une classe des quations fonctionnelles)”)中使用了法语“noyau(核)”(365-390页)。 David …...
defcon-quals 2023 crackme.tscript.dso wp
将dso文件放到data/ExampleModule目录下,编辑ExampleModule.tscript文件 function ExampleModule::onCreate(%this) { trace(true); exec("./crackme"); __main("aaaaaaaa"); quit(); } 然后点击主目录下的Torque3D-debug.bat就可以在生成的c…...

前端开发 vs. 后端开发:编程之路的选择
文章目录 前端开发:用户界面的创造者1. HTML/CSS/JavaScript:2. 用户体验设计:3. 响应式设计:4. 前端框架: 后端开发:数据和逻辑的构建者1. 服务器端编程:2. 数据库:3. 安全性&#…...

算法练习4——删除有序数组中的重复项 II
LeetCode 80 删除有序数组中的重复项 II 给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。 不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 …...
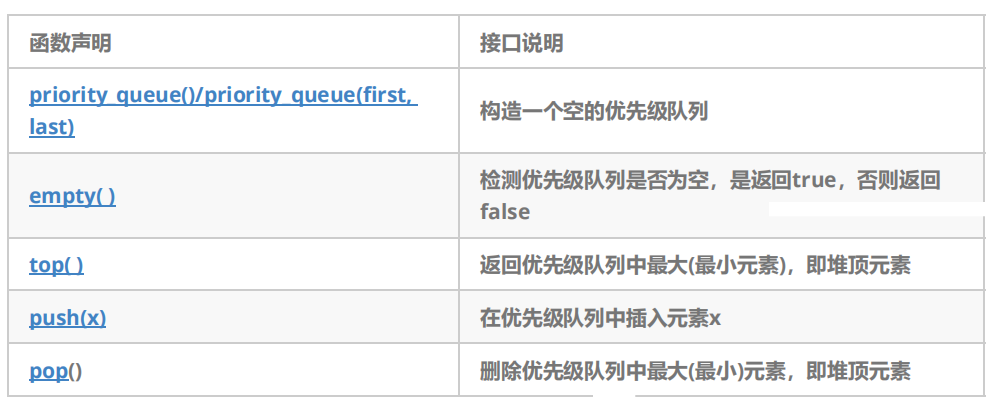
【C++进阶(六)】STL大法--栈和队列深度剖析优先级队列适配器原理
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:C从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习C 🔝🔝 栈和队列 1. 前言2. 栈和队列的接口函数熟悉3. …...

linux opensuse使用mtk烧录工具flashtool
环境 linux发行版:opensuse leap 15.5 工具:SP_Flash_Tool_Selector_exe_Linux_v1.2316.00.100.rar 或其他版本 目标:mtk设备 下载链接 https://download.csdn.net/download/zmlovelx/88382784 或网络搜索。 使用 opensuse可直接解压后使…...
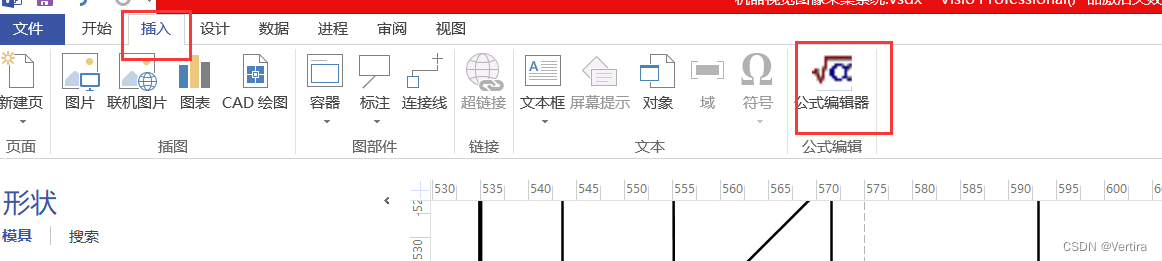
Visio如何对文本打下标、上标,以及插入公式编辑器等问题(已解决)
解决这个问题的本质问题,就是在Visio中插入公式编辑器(这不是visio的常用命令,需要添加)。 打开Visio--》文件--选项 点击选项,弹出对话框。在自定义功能区中,点击 常用命令,在下拉选项中&#…...
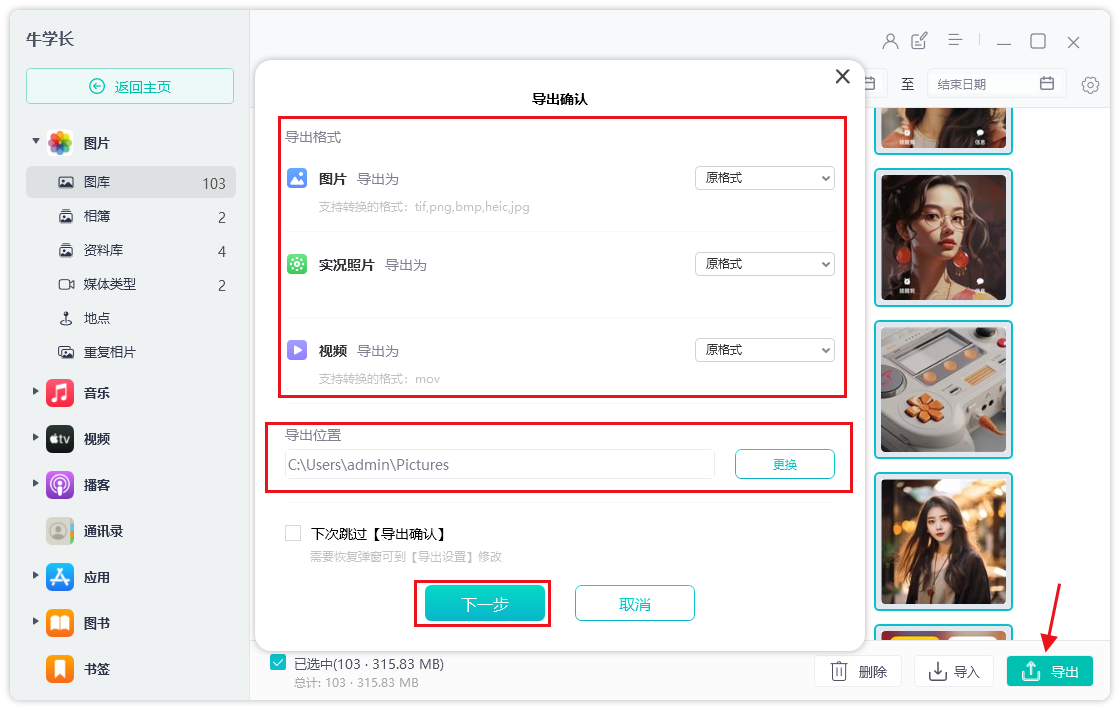
快速将iPhone大量照片快速传输到电脑的办法!
很多使用iPhone 的朋友要将照片传到电脑时,第一时间都只想到用iTunes 或iCloud,但这2个工具真的都非常难用,今天小编分享牛学长苹果数据管理工具的照片传输功能,他可以快速的将iPhone照片传输到电脑上,并且支持最新的i…...

TCP/IP协议簇包含的协议
应用层(Application Layer): HTTP(Hypertext Transfer Protocol):用于Web浏览器和Web服务器之间的通信。HTTPS(Hypertext Transfer Protocol Secure):安全的HTTP版本&…...
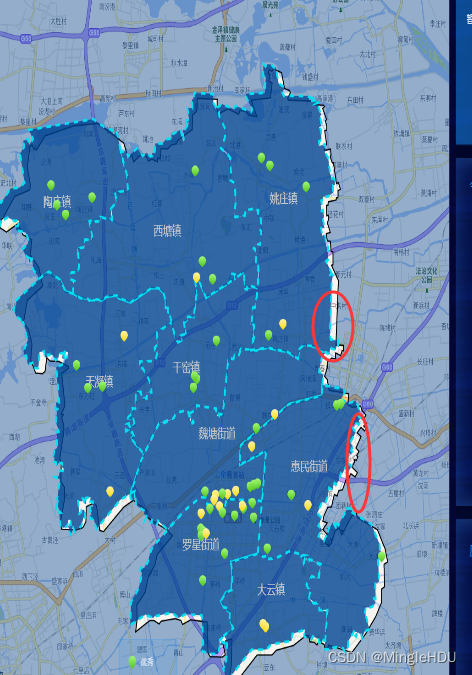
天地图绘制区域图层
背景: 业务方要求将 原效果图 参考效果图 最终实现效果 变更点: 1.将原有的高德地图改为天地图 2.呈现形式修改:加两层遮罩:半透明遮罩层mask区域覆盖物mask 实现过程: 1.更换地图引入源 <link rel"style…...

git权限不够:Ask a project Owner or Maintainer to create a default branch
新仓库还未创建任何分支时,Developer角色时首次提交代码,抛如下异常 remote: GitLab: remote: A default branch (e.g. master) does not yet exist for galaxy/apache-jspf-project remote: Ask a project Owner or Maintainer to cre…...
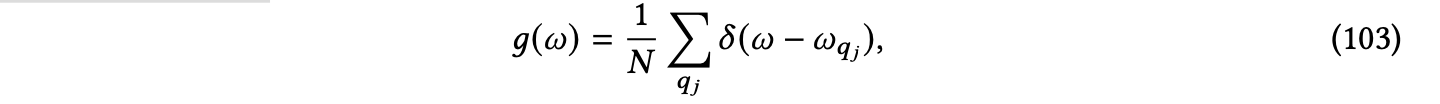
AI在材料科学中的应用
7 AI在材料科学中的应用 在这一部分,我们将讨论AI技术在材料科学中的应用。首先,我们将介绍晶体材料的概述,并详细定义晶体材料的物理对称性,具体在第7.1节中讨论。接下来,我们将在第7.2节和第7.3节中讨论两个常见且基…...

VSCode快速设置heder和main函数
快速设置header: 点击左侧的齿轮,选择User Snippets: 在出现的选择框中输入python,选择python.json 在最外层的{ }内部添加以下内容 "HEADER": {"prefix": "header","body": ["# -*- encoding:…...
JimuReport积木报表 v1.6.2 版本正式发布—开源免费的低代码报表
项目介绍 一款免费的数据可视化报表,含报表和大屏设计,像搭建积木一样在线设计报表!功能涵盖,数据报表、打印设计、图表报表、大屏设计等! Web 版报表设计器,类似于excel操作风格,通过拖拽完成报…...

sqlsession对象为什么不能被共享?
因为它是一个非线程安全的对象。每个SQLSession对象都维护了一个独立的数据库连接,以及与该连接相关的事务和缓存。如果多个线程共享同一个SQLSession对象,可能会导致数据混乱、事务冲突等问题。另外,SQLSession对象还包含了一级缓存…...
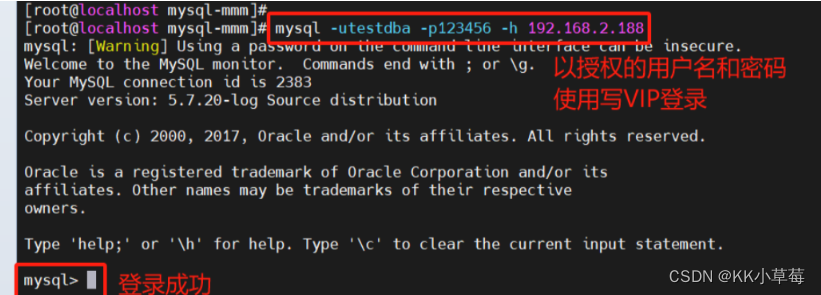
MySQL MMM高可用架构
MySQL MMM高可用架构一、MMM概述1、MMM简介2、MMM高可用架构3、MMM故障切换流程 二、MMM高可用双主双从架构部署1、配置主主复制(master),主从复制(slave)1)修改 Master1的MySQL配置文件2)把配置…...
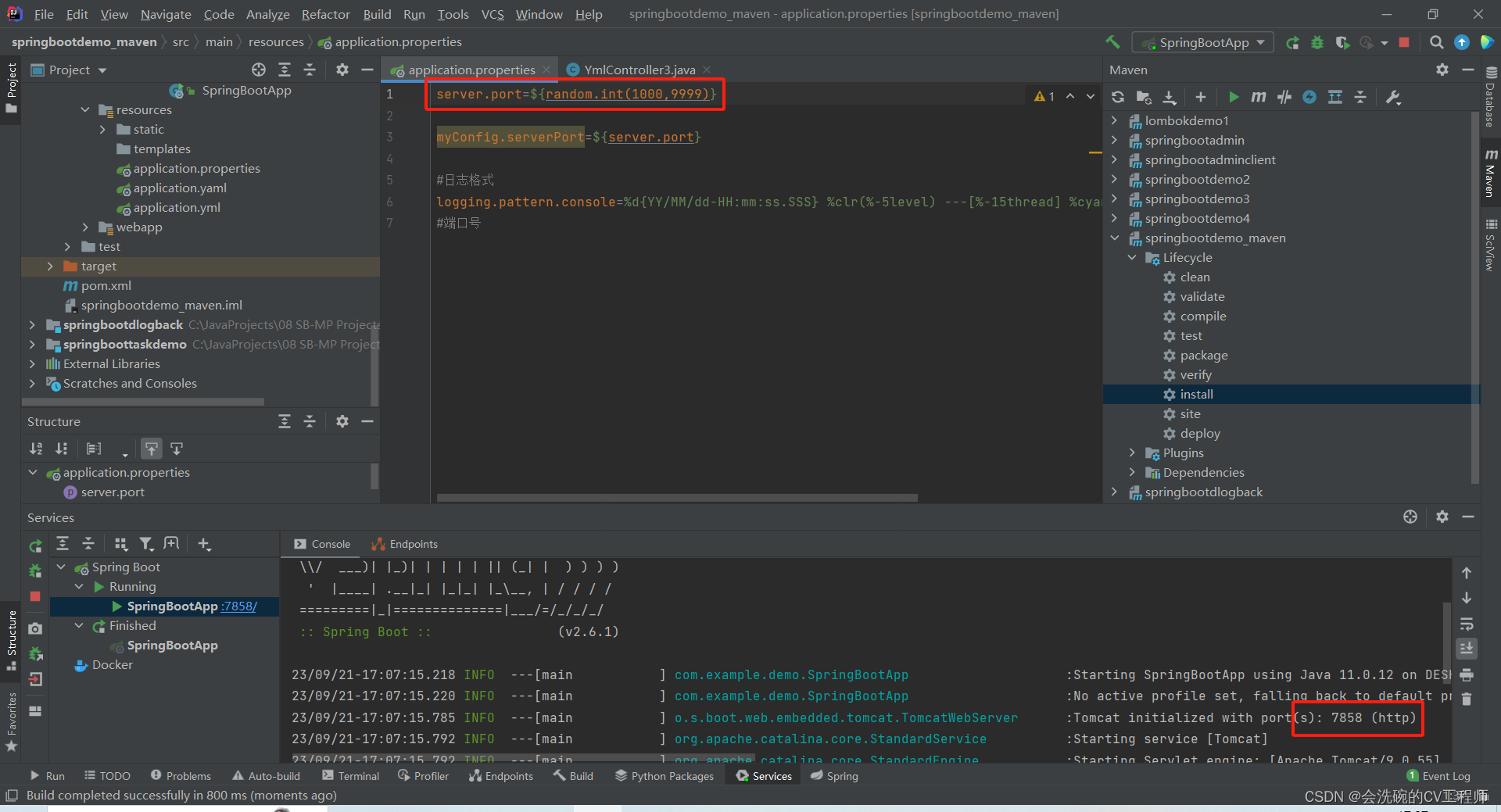
Spring Boot中配置文件介绍及其使用教程
目录 一、配置文件介绍 二、配置简单数据 三、配置对象数据 四、配置集合数据 五、读取配置文件数据 六、占位符的使用 一、配置文件介绍 SpringBoot项目中,大部分配置都有默认值,但如果想替换默认配置的话,就可以使用application.prop…...

Hobby脚本自动化工具
Hobby脚本自动化工具 功能简介:可以按照指定编排的配置文件,按顺序执行并监听 使用场景:可以用在前期信息收集的步骤上,将一些常见的脚本进行归纳,并编写成配置文档进行自动化处理 优点:可以扩展性强&am…...
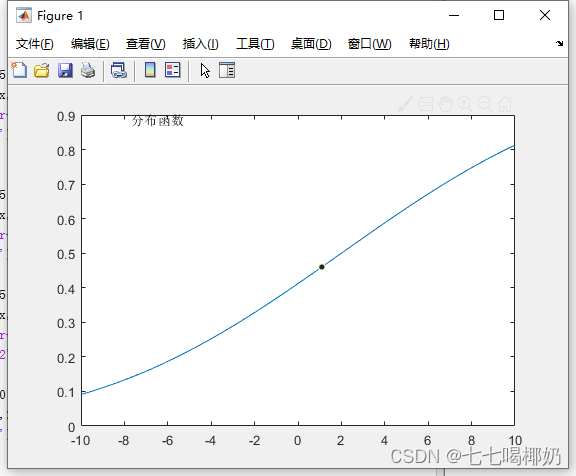
Matlab随机数的产生
1、常见分布随机数的产生 1.1 二项分布 在贝努力试验中,某事件A发生的概率为p,重复该实验n次,X表示这n次实验中A发生的次数,则随机变量X服从的概率分布律(概率密度)为 记为 binopdf(x,n,p) p…...

计算机网络 第四章:网络层
一.网络层概述 1.1分组转发和路由选择 网络层的主要任务就是将分组从源主机经过多个网络和多段链路传输到目的主机,可以将该任务划分为分组转发和路由选择两种重要的功能。 如图所示:这些异构型网络如果只是需要各自内部通信,那它们只需要实…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...
