Matlab随机数的产生
1、常见分布随机数的产生
1.1 二项分布
在贝努力试验中,某事件A发生的概率为p,重复该实验n次,X表示这n次实验中A发生的次数,则随机变量X服从的概率分布律(概率密度)为
记为 ![]()
binopdf(x,n,p) pdf('bino',x,n,p)
返回参数为n和p的二项分布在x处的密度函数值(概率分布律值)。
>> clear
>> x=1:30;y=binopdf(x,300,0.05);
plot(x,y,'b*')

binocdf(x,n,p) cdf('bino',x,n,p)
返回参数为n和p的二项分布在x处的分布函数值
>> clear
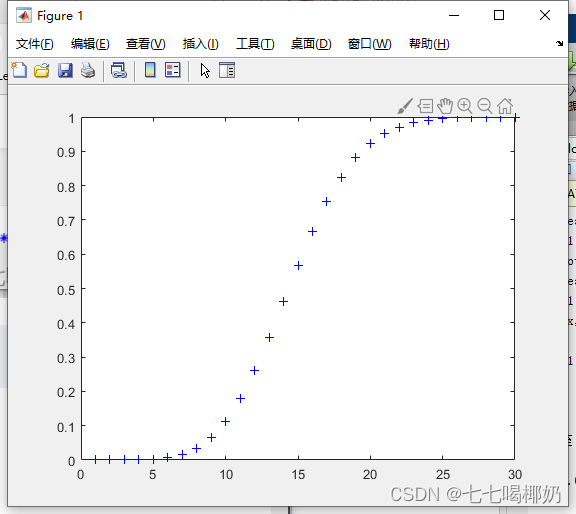
>> x=1:30;y=binocdf(x,300,0.05);
>> plot(x,y,'b+')
icdf('bino',q,n,p)
逆分布计算,返回参数为n和p的二项分布的分布函数当概率为q时的x值。
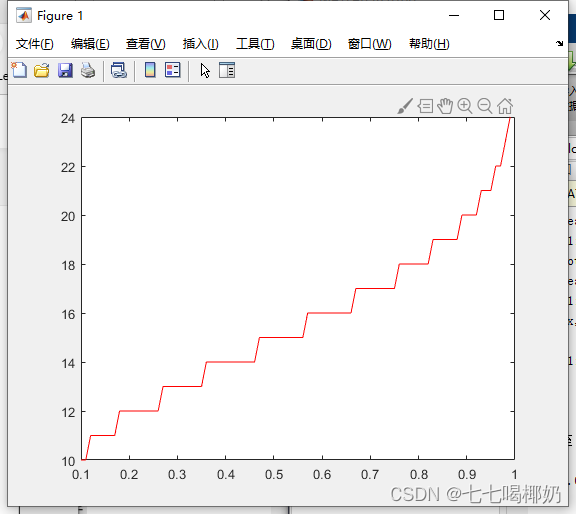
>> p=0.1:0.01:0.99;
>> x=icdf('bino',p,300,0.05);
>> plot(p,x,'r-')
R=binornd(n,p,m1,m2)
产生m1行m2列的服从参数为n和p的二项分布的随机数据。
>> R=binornd(10,0.5,3,4)
R =0 6 5 56 6 5 54 5 5 4>> A=binornd(10,0.2,3)
A =1 2 21 3 12 2 2
1.2 泊松分布
泊松分布描述密度问题:比如显微镜下细菌的数量X,单位人口里感染某疾病的人口数X,单位时间内来到交叉路口的人数X(或车辆数X),单位时间内某手机收到的信息的条数X,等等。
X的分布律为(密度函数)
记为![]() 其中参数λ表示平均值。
其中参数λ表示平均值。
poisspdf(x,lambda) pdf('poiss',x,lambda)
返回参数为lambda的泊松分布在x处的概率值。
>> clear
>> x=0:30;p=pdf('poiss',x,4);
>> plot(x,p,'b+')

poisscdf(x,lambda) cdf('poiss',x,lambda)
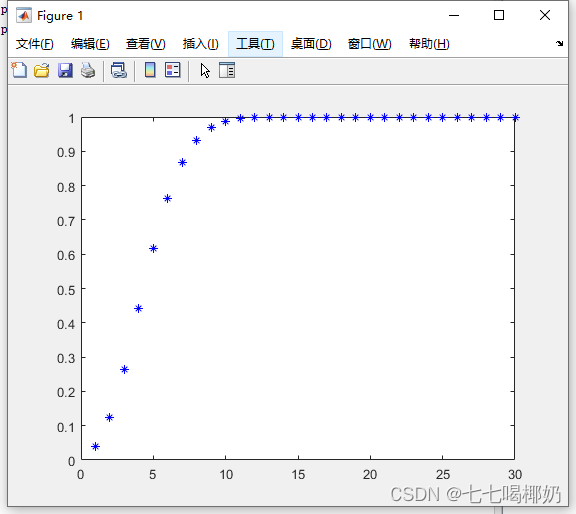
返回参数为lambda的泊松分布在x处的分布函数值: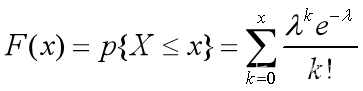
>> x=1:30;
>> p=cdf('poiss',x,5);
>> plot(x,p,'b*')
poissrnd(lambda,m1,m2)
返回m1行m2列的服从参数为lambda的泊松分布的随机数。
>> poissrnd(10,3,4)ans =15 10 9 714 10 7 910 9 14 10
>> poissrnd(10,3)ans =14 11 88 11 135 10 11
1.3 几何分布
在伯努利试验中,每次试验成功的概率为p,失败的概率为q=1-p,0<p<1。首次试验成功发生在第X次,则X的分布律为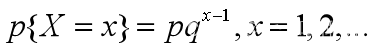
geopdf(x,p)
返回服从参数为p的几何分布在x处的概率值。
>> x=1:20;
>> p=geopdf(x,0.05);
>> plot(x,p,'*')
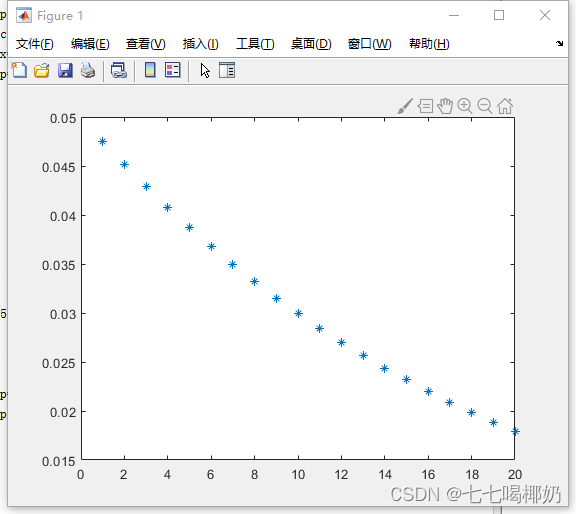
>> x=1:20;
>> p=cdf('geo',x,0.05);
>> plot(x,p,'+')
返回分布函数值
>> R=geornd(0.2,3,4)
R =0 0 5 00 2 2 89 10 0 0
>> R1=geornd(0.2,3)
R1 =0 8 13 3 00 0 1
1.4 均匀分布(离散,等可能分布)

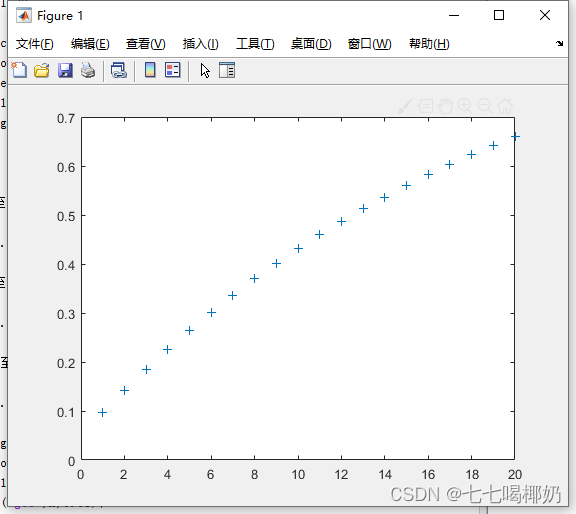
>> x=1:20;
>> p=unidpdf(x,20);f=unidcdf(x,20);
>> plot(x,p,'*',x,f,'+')

>> R=unidrnd(20,3,4)
R =1 14 8 1517 16 14 119 15 4 6
>> R=unidrnd(20,3)
R =1 14 12 7 917 20 8
1.5 均匀分布(连续型等可能)

>> clear
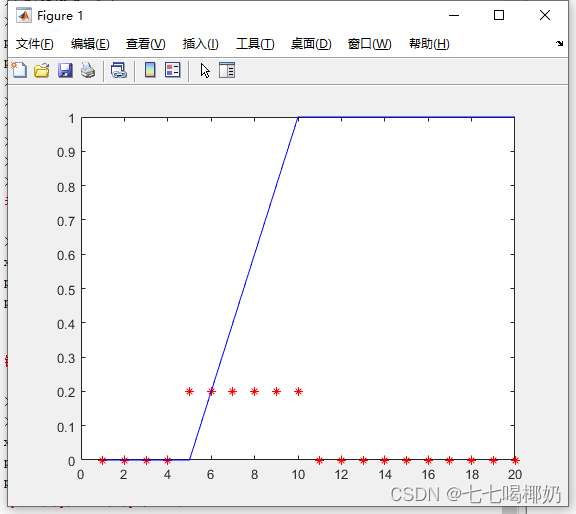
>> x=1:20;p=unifpdf(x,5,10);
>> p1=unifcdf(x,5,10);
>> plot(x,p,'r*',x,p1,'b-')
>> R=unifrnd(5,10,3,4)
R =8.8276 7.4488 8.5468 8.39858.9760 7.2279 8.7734 8.27555.9344 8.2316 6.3801 5.8131>> R1=unifrnd(5,10,3)
R1 =5.5950 6.7019 8.75637.4918 7.9263 6.27559.7987 6.1191 7.5298
1.6 指数分布(描述“寿命”问题)
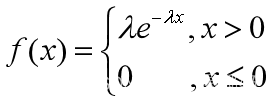
>> x=0:0.1:10;
p=exppdf(x,5);
p1=expcdf(x,5);
plot(x,p,'*',x,p1,'-')
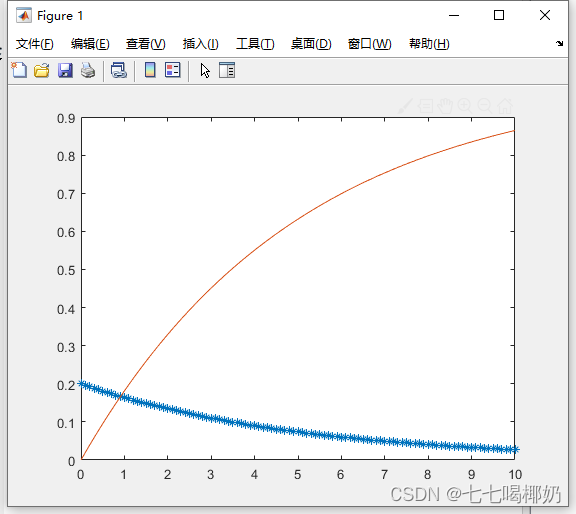
>> R=exprnd(5,3,4)
R =1.7900 3.0146 6.7835 1.02720.5776 9.8799 0.8675 7.06270.2078 9.5092 6.8466 0.3668>> R1=exprnd(5,3)
R1 =5.2493 2.4222 0.92678.1330 3.7402 2.67856.9098 5.2255 2.9917
1.7 正态分布
![]()
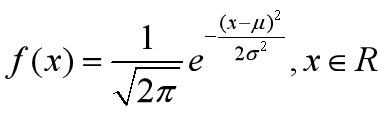
clear
x=-10:0.1:15;
p1=normpdf(x,2,4);p2=normpdf(x,4,4);p3=normpdf(x,6,4);
plot(x,p1,'r-',x,p2,'b-',x,p3,'g-'),
gtext('mu=2'),gtext('mu=4'),gtext('mu=6')

clear
x=-10:0.1:15;
p1=normpdf(x,4,4);p2=normpdf(x,4,9);p3=normpdf(x,4,16);
plot(x,p1,'r-',x,p2,'b-',x,p3,'g-'),
gtext('sig=2'),gtext('sig=3'),gtext('sig=4')

>> clear
>> x=-10:0.1:10;
>> p=normcdf(x,2,9);
>> plot(x,p,'-'),gtext('分布函数')
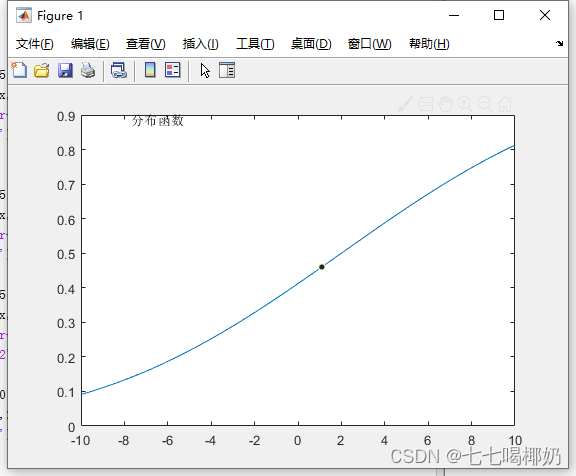
>> p=[0.01,0.05,0.1,0.9,0.05,0.975,0.9972];
>> x=icdf('norm',p,0,1)
x =
-2.3263 -1.6449 -1.2816
1.2816 -1.6449 1.96 2.7703
x=icdf('norm',p,0,1)
计算标准正态分布的分布函数的反函数值,即知道概率情况下,返回相应的分位数。
产生正态分布的随机数
>> R=normrnd(0,1,3,4)
R =1.5877 0.8351 -1.1658 0.7223-0.8045 -0.2437 -1.1480 2.58550.6966 0.2157 0.1049 -0.6669
>> R1=normrnd(0,1,3)
R1 =0.1873 -0.4390 -0.8880-0.0825 -1.7947 0.1001-1.9330 0.8404 -0.5445
相关文章:

Matlab随机数的产生
1、常见分布随机数的产生 1.1 二项分布 在贝努力试验中,某事件A发生的概率为p,重复该实验n次,X表示这n次实验中A发生的次数,则随机变量X服从的概率分布律(概率密度)为 记为 binopdf(x,n,p) p…...

计算机网络 第四章:网络层
一.网络层概述 1.1分组转发和路由选择 网络层的主要任务就是将分组从源主机经过多个网络和多段链路传输到目的主机,可以将该任务划分为分组转发和路由选择两种重要的功能。 如图所示:这些异构型网络如果只是需要各自内部通信,那它们只需要实…...

分享一个docker无法启动的小问题
准备看看docker服务怎么样 [rootlocalhost ~]# docker ps Cannot connect to the Docker daemon at unix:///var/run/docker.sock. Is the docker daemon running? 这一看就是docker的进程崩了,我们启动下进程 [rootlocalhost ~]# systemctl start docker Faile…...

Linux 安全 - Capabilities机制
文章目录 前言一、简介二、Capabilities list2.1 POSIX-draft defined capabilities2.2 Linux-specific capabilities 三、 Past and current implementation四、Thread capability sets五、File capabilities六、Transformation of capabilities during execve()七、Capabilit…...

分布式搜索引擎es-3
文章目录 数据聚合聚合的种类RestAPI实现聚合 数据聚合 什么是聚合? 聚合可以让我们极其方便的实现对数据的统计、分析、运算。例如: 什么品牌的手机最受欢迎?这些手机的平均价格、最高价格、最低价格?这些手机每月的销售情况如…...
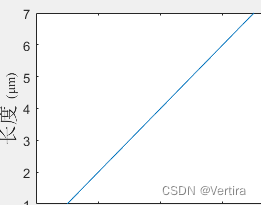
Matlab坐标轴标签中文设置宋体
对y坐标输出中文宋体 新罗马字符 x[1,2,3,4,5,6,7]; plot(x) ylabel(\fontname{宋体}\fontsize{20}长度\fontname{Times New Roman}\fontsize{10} (μm))可以灵活设置字体和大小,其图片如下图所示 也可以对全图的文字设置同一个字体 set(gca,FontSize,9,Fontname, Times New…...

做一个贪吃蛇小游戏happy一下
直接Vue上代码 <template><div><div>贪吃蛇</div><canvas id"canvas" width"400" height"400"></canvas></div> </template><script> export default {data() {return {ctx: null,inter…...
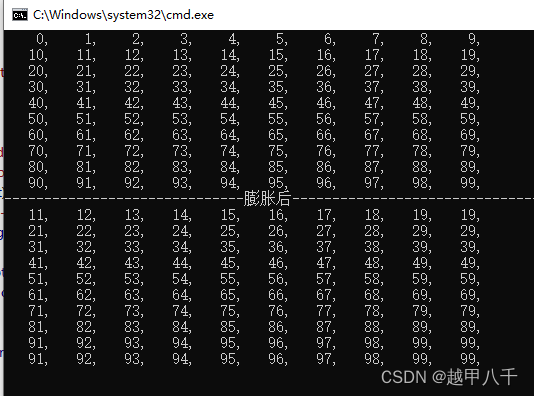
opencv形态学-膨胀
opencv形态学-膨胀 膨胀就是取每一个位置结构元邻域内最大值作为该位置的输出灰度值; 膨胀是取邻域内最大值,那么显然膨胀后图像整体亮度会比原先要高,图像中亮的物体尺寸会变大,相反暗的尺寸会减小,甚至是消失 结构元…...

玄子Share 设计模式 GOF 全23种 + 七大设计原则
玄子Share 设计模式 GOF 全23种 七大设计原则 前言: 此文主要内容为 面向对象七大设计原则(OOD Principle)GOF(Gang Of Four)23种设计模式拓展的两个设计模式 简单工厂模式(Simple Factory Pattern&#x…...

单链表操作 C实现
struct LNode { //定义一个节点 int data; //数据域 struct LNode *next; //指针域 }; 0.初始化 typedef sturct LNode{ //定义单链表结点类型 int date ; //每个结点存放一个数据元素struct LNode *next; //指针指向下…...
WordPress主题网站首页添加好看的四格小工具教程
直接到网站根目录创建一个css文件(文件名:sige.css),文件名可自定义(注意文件名一致) <link rel"stylesheet" href"你的网站/sige.css" type"text/css" > 然后在header.php模板最上方添加引入代码 也可自定义HTML里添加css代码最上方写…...

unittest自动化测试框架讲解以及实战
为什么要学习unittest 按照测试阶段来划分,可以将测试分为单元测试、集成测试、系统测试和验收测试。单元测试是指对软件中的最小可测试单元在与程序其他部分相隔离的情况下进行检查和验证的工作,通常指函数或者类,一般是开发完成的。 单元…...

数学建模之Matlab基础操作
作者由于后续课程也要学习Matlab,并且之前也进行了一些数学建模的练习(虽然是论文手),所以花了几天零碎时间学习Matlab的基础操作,特此整理。 基本运算 a55 %加法,同理减法 b2^3 %立方 c5*2 %乘法 x 1; …...

【Nuxt】04 Nuxt2-SEO: sitemap.xml、seo优化、robots.txt
1 SiteMap设置 环境准备 注意生成sitemap依赖于nuxtjs/sitemap,并且需要用axios进行请求,不要使用nuxtjs/axios,不然会报错 sitemap.xml配置 在nuxt.config.js中配置下面的内容 npm install nuxtjs/sitemap npm install axios在static/s…...

VMware VSAN 入门
一、虚拟化的存储 1.1、对于数据中心来说最重要的是数据,而承载数据的设备就是存储设备(Storage) 1.2、物理服务器的本地存储阵列 与 虚拟化服务器的本地存储阵列 对比 1.3、避免单台服务器故障的虚拟化高级特性:vSphere HA技术 …...
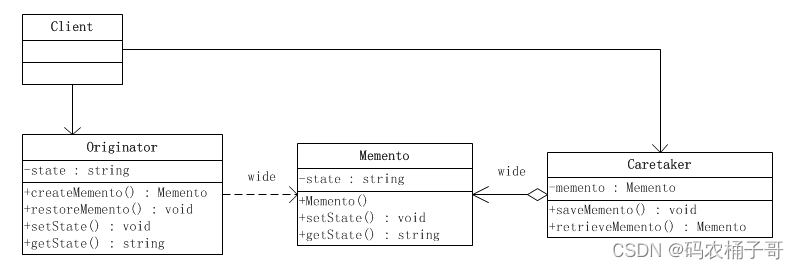
【设计模式】备忘录模式
文章目录 1.备忘录模式定义2.备忘录模式的角色3.备忘录模式实现3.1.场景说明3.2.结构类图3.3.代码实现 4.备忘录模式优缺点5.备忘录模式适用场景6.备忘录模式总结 主页传送门:💁 传送 1.备忘录模式定义 备忘录(Memento Pattern)模…...

vue3+elementUiPlus表格导出功能
1.下载需要的组件包 npm install file-saver xlsx 2.页面中导入 import FileSaver from file-saver import * as XLSX from xlsx; 3.页面中的表格加一个id <el-table :data"tableData" ref"multipleTableRef" style"width…...

专题五:优先级队列
"你了解我,最干净的轮廓, 握住小小风车和放肆的梦~" 堆是一个不错的数据结构,而在计算机中,无法表示二叉分支结构,因此我们经常会看到使用线性表来作为堆的存储容器。在接触堆的时候,我们是把它…...

游戏设计模式专栏(一):工厂方法模式
引言 大家好,我是亿元程序员,一位有着8年游戏行业经验的主程。 本系列是《和8年游戏主程一起学习设计模式》,让糟糕的代码在潜移默化中升华,欢迎大家关注分享收藏订阅。 在游戏开发中,代码的组织和结构对于项目的可…...
element中使用el-steps 进度条效果demo(整理)
<template><div class"margin-top20"><!-- align-center 不要居中就去掉 --><!-- process-status 这几个参数值:改变颜色 wait / process / finish / error / --><!-- active 到第几个是绿色 --><el-steps :space&qu…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
