专题五:优先级队列

"你了解我,最干净的轮廓, 握住小小风车和放肆的梦~"
堆是一个不错的数据结构,而在计算机中,无法表示二叉分支结构,因此我们经常会看到使用线性表来作为堆的存储容器。在接触堆的时候,我们是把它拿来同其他排序算法来看待的,但其实我们经常使用的是快排或者归并亦或者性能更加优越的"选择快排"。堆的应用场景,实质上转移到了查找问题,例如TopK等。很多语言也提供了以堆为底层的数据结构,例如C++中的priority_queue,Java中的PriorityQueue……
如何实现一个堆排序?
我们对任意一个堆的定义是一个完全二叉树,当一个父节点的值,大于左右子节点的值,则称为大堆,反之如果一个父节点的值,小于左右节点的值,则被称之为小堆。
建堆的方法有两种,一种是"向上调整法",一种是"向下调整法"。前者的思想是着眼于整个数组,后者的思想着眼于分治,先将最小的子树进行一次堆排序,再不停向上迭代。因为"向下调整法"实现起来更为简单,并且效率更高,所以我们选择后者。
(1) 构建一个堆(大堆)
// 找到最后的父节点
for (int i = (n - 1 - 1 ) / 2;i >= 0;--i)
{adjustDown(nums, i);
}void adjustDown(vector<int>& nums,int parent)
{// 控制下标int n = nums.size();int child = parent * 2 + 1;while (child < n){// 把更大的换上去if (child+1 < n && nums[child] < nums[child + 1]) child++;// 比较if (nums[parent] < nums[child]) {swap(nums[parent], nums[child]);// 更新parent = child;child = parent * 2 + 1;}else {// 结束break;}}
}
(2) 堆排序
要实现"升序排序,构建大堆,反之构建小堆"(因为本篇不是着眼于堆排序,不解释)。
void adjustDown(vector<int>& nums,int parent,int end)
{// 控制下标int child = parent * 2 + 1;while (child < end){// 把更大的换上去if (child+1 < end && nums[child] < nums[child + 1]) child++;// 比较if (nums[parent] < nums[child]) {swap(nums[parent], nums[child]);// 更新parent = child;child = parent * 2 + 1;}else {// 结束break;}}
}void HeapSort(vector<int>& nums)
{// 建堆int n = nums.size();// 找到最后的父节点for (int i = (n - 1 - 1 ) / 2;i >= 0;--i){adjustDown(nums, i,n);}// 排序int end = n - 1;while (end > 0){// 因为构建的是大堆,所有后面的数一定是小数swap(nums[end], nums[0]); // 同堆顶交换 让最大的数 在最后一个adjustDown(nums, 0,end);// 排序好一个数end--;}for (auto& n : nums)cout << n << " ";cout << endl;
}
——前言
1、最后一块石头的重量
(1) 题目解析 
(2) 算法原理 
C++:
class Solution {
public:int lastStoneWeight(vector<int>& stones) {// 寻找大数,构建大堆priority_queue<int,vector<int>,less<int>> heap;// 入队列for(auto& n:stones) heap.push(n);// 模拟出队列while(heap.size() > 1){int x = heap.top();heap.pop();int y = heap.top();heap.pop();// 插入差值heap.push(x-y);}return heap.size() == 0 ? 0:heap.top();}
};Java:
class Solution {public int lastStoneWeight(int[] stones) {PriorityQueue<Integer> heap = new PriorityQueue<>((a, b) -> b - a);for(int n:stones) heap.offer(n);// 模拟while(heap.size() > 1){int a = heap.poll();int b= heap.poll();heap.offer(a-b);}return heap.isEmpty() ? 0 : heap.peek();}
}2、数据流中的第K大元素
(1) 题目解析
 这也是一个经典的topK问题,对于要找第K大的数,我们需要构建是小堆,而不是大堆。反之,要查找第K小的数,我们需要构建的是大堆,而不是小堆。
这也是一个经典的topK问题,对于要找第K大的数,我们需要构建是小堆,而不是大堆。反之,要查找第K小的数,我们需要构建的是大堆,而不是小堆。
(2) 算法原理

c++:
class KthLargest {
public:// 构建小堆priority_queue<int,vector<int>,greater<int>> _heap;int _k; // 构建多大的kKthLargest(int k, vector<int>& nums) {_k = k;// 入队列for(auto& n:nums){_heap.push(n);if(_heap.size() > _k) _heap.pop(); // 剔除多余数}}int add(int val) {_heap.push(val);if(_heap.size() > _k) _heap.pop();return _heap.top();}
};java:
class KthLargest {PriorityQueue<Integer> heap;int _k;public KthLargest(int k, int[] nums) {_k = k;heap = new PriorityQueue<>(); // 默认是小堆for(int x:nums){heap.offer(x);if(heap.size() > _k) heap.poll();}}public int add(int val) {heap.offer(val);if(heap.size() > _k) heap.poll();return heap.peek();}
}3、前K个高频单词
(1) 题目解 
(2) 算法原理
class Solution {
public:typedef pair<int,string> PSI; // 频次与字符串 用于比较struct cmp{template<class T>bool operator()(T& t1,T& t2){return (t1.first > t2.first) || (t1.first == t2.first) && (t1.second < t2.second);}};vector<string> topKFrequent(vector<string>& words, int k) {unordered_map<string,int> hash; // 统计频次for(auto& str:words) hash[str]++;// 普通的比较函数: less\greater 不能满足我们的要求// 所以我们得更换比较函数: 这里我们采用的是 仿函数priority_queue<PSI,vector<PSI>,cmp> heap;for(auto& n:hash){heap.push({n.second,n.first});if(heap.size() > k) heap.pop();}// 倒序vector<string> ret(k);for(int i=k-1;i>=0;--i){ret[i] = heap.top().second;heap.pop();}return ret;}
};4、数据流中的中位数
(1) 题目解析

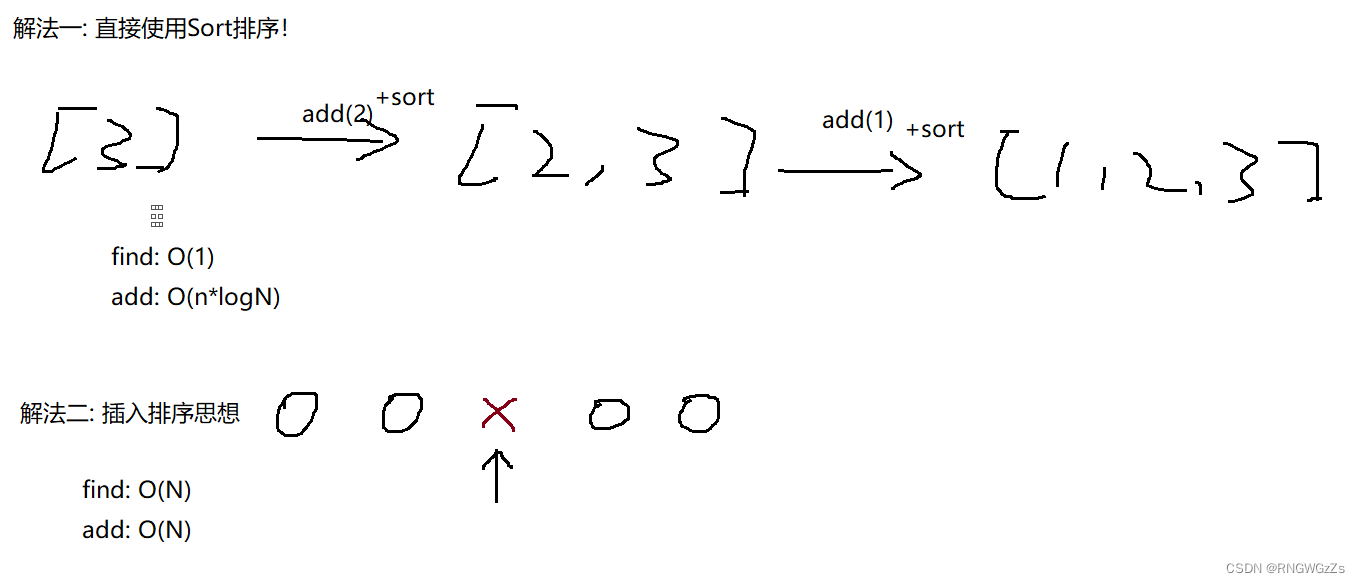
前两者解法都是很好想的,前提就是保证数组有序,再来找中位数。但,我们这里选择的解法不是其中的任意一种。
(2) 算法原理 
class MedianFinder {
public:priority_queue<int,vector<int>,less<int>> _left;priority_queue<int,vector<int>,greater<int>> _right;MedianFinder() {}void addNum(int num) {if(_left.size() == _right.size()){if(_left.empty() || num <= _left.top()){// 直接进入_left.push(num);}else{// 替换_right.push(num);_left.push(_right.top());_right.pop();}}else{if(num <= _left.top()){_left.push(num);_right.push(_left.top());_left.pop();}else{_right.push(num);}}}double findMedian() {if(_left.size() == _right.size()) return (_left.top() + _right.top()) / 2.0;return _left.top(); // m=n+1}
};本篇到此结束,感谢你的阅读。
祝你好运,向阳而生~

相关文章:

专题五:优先级队列
"你了解我,最干净的轮廓, 握住小小风车和放肆的梦~" 堆是一个不错的数据结构,而在计算机中,无法表示二叉分支结构,因此我们经常会看到使用线性表来作为堆的存储容器。在接触堆的时候,我们是把它…...

游戏设计模式专栏(一):工厂方法模式
引言 大家好,我是亿元程序员,一位有着8年游戏行业经验的主程。 本系列是《和8年游戏主程一起学习设计模式》,让糟糕的代码在潜移默化中升华,欢迎大家关注分享收藏订阅。 在游戏开发中,代码的组织和结构对于项目的可…...
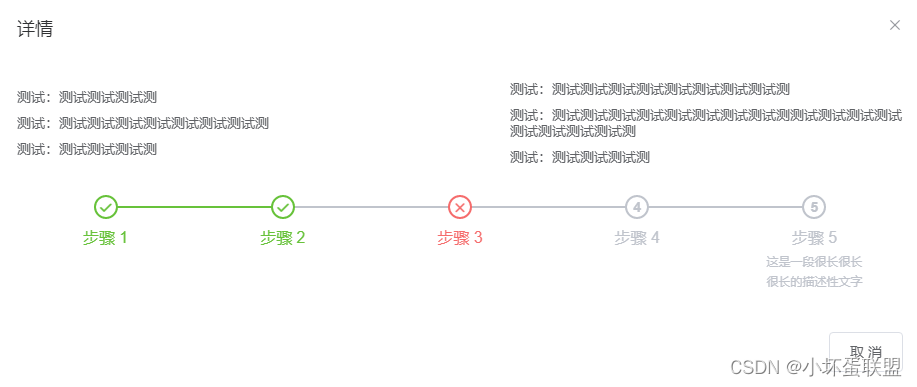
element中使用el-steps 进度条效果demo(整理)
<template><div class"margin-top20"><!-- align-center 不要居中就去掉 --><!-- process-status 这几个参数值:改变颜色 wait / process / finish / error / --><!-- active 到第几个是绿色 --><el-steps :space&qu…...
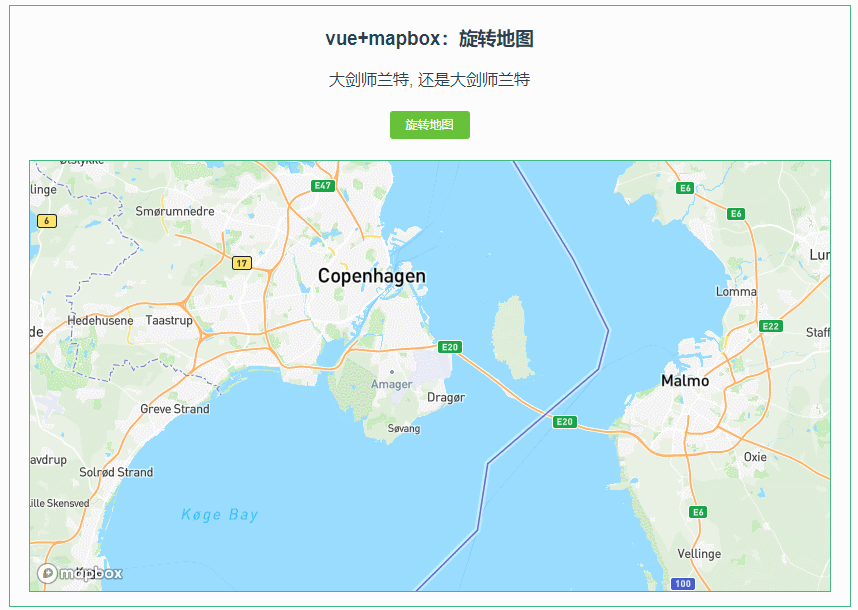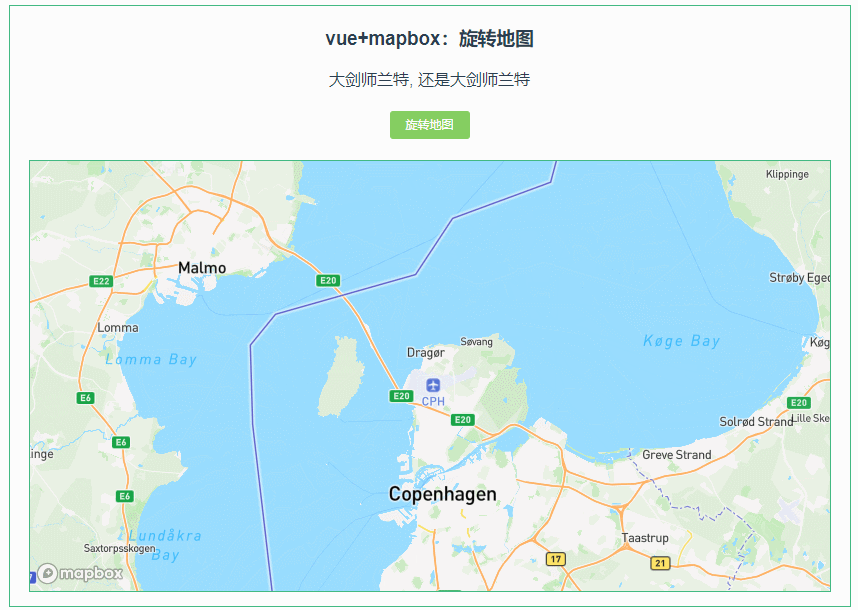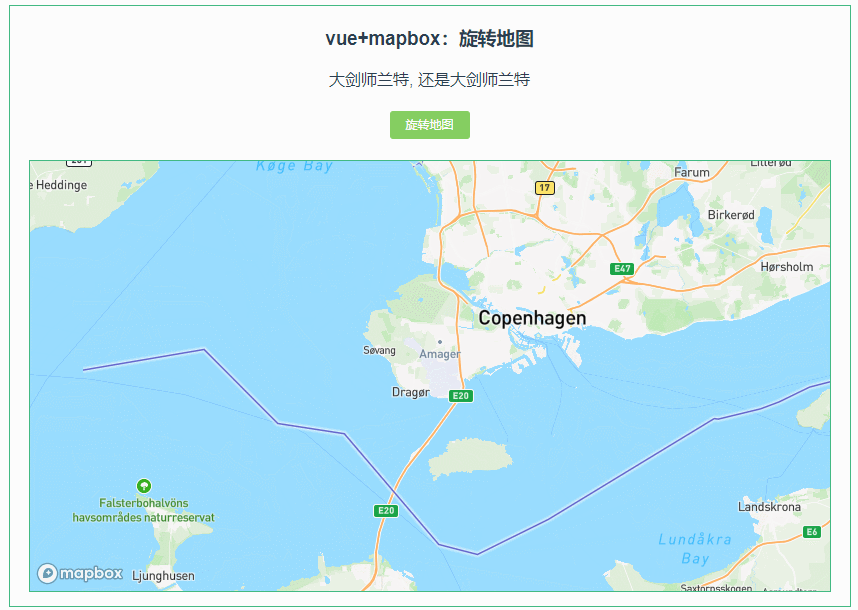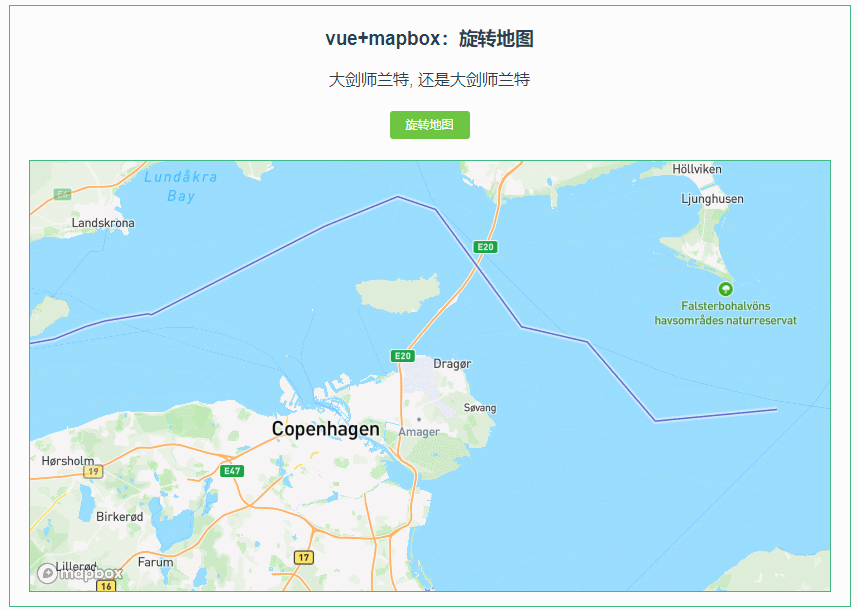
038:mapboxGL 旋转地图(rotateTo)
第038个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+mapbox中旋转地图。 直接复制下面的 vue+mapbox源代码,操作2分钟即可运行实现效果 文章目录 示例效果配置方式示例源代码(共68行)相关API参考:专栏目标示例效果 配置方式 1)查看基础设置:https://xiaozhuan…...
java遇到的问题
java遇到的问题 Tomcat与JDK版本问题 当使用Tomcat10的版本用于springmvc借用浏览器调试时,使用JDK8浏览器会报异常。 需要JDK17(可以配置多个JDK环境,切换使用)才可以使用,配置为JAVA_HOME路径,否则&a…...

LLM(二)| LIMA:在1k高质量数据上微调LLaMA1-65B,性能超越ChatGPT
本文将介绍在Lit-GPT上使用LoRA微调LLaMA模型,并介绍如何自定义数据集进行微调其他开源LLM 监督指令微调(Supervised Instruction Finetuning) 什么是监督指令微调?为什么关注它? 目前大部分LLM都是decoder-only&…...
)
Android AMS——创建Application(七)
与在 App 内部启动一个 Activity 的不同之处在于,点击桌面 Launcher 首次启动一个应用程序的时候,会先去创建一个该应用程序对应的进程,然后执行 ActivityThread 的 main() 方法去创建该应用对应的 Application,然后再去启动首页 Activity。前面已经分析了进程的创建和启动…...

html 边缘融合加载
html 代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>边缘融合加载</title><style>* {margin: 0;padding: 0;box-sizing: border-box;}body {height: 100vh;padding-bottom: 80px;b…...

ElasticSearch - 在 微服务项目 中基于 RabbitMQ 实现 ES 和 MySQL 数据异步同步(考点)
目录 一、数据同步 1.1、什么是数据同步 1.2、解决数据同步面临的问题 1.3、解决办法 1.3.1、同步调用 1.3.2、异步通知(推荐) 1.3.3、监听 binlog 1.3、基于 RabbitMQ 实现数据同步 1.3.1、需求 1.3.2、在“酒店搜索服务”中 声明 exchange、…...
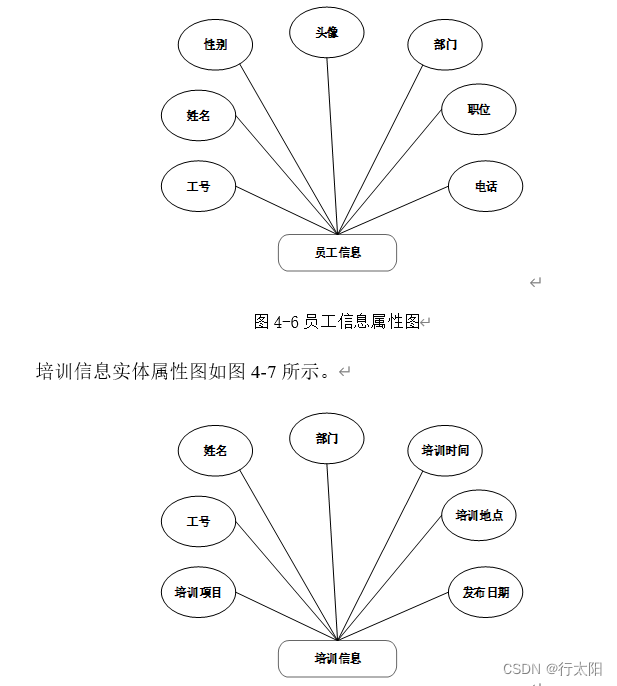
Springboot+vue的企业人事管理系统(有报告),Javaee项目,springboot vue前后端分离项目。
演示视频: Springbootvue的企业人事管理系统(有报告),Javaee项目,springboot vue前后端分离项目。 项目介绍: 本文设计了一个基于Springbootvue的前后端分离的企业人事管理系统,采用M(model&am…...

初识Java 11-1 函数式编程
目录 旧方式与新方式 lambda表达式 方法引用 Runnable 未绑定方法引用 构造器方法引用 函数式接口 带有更多参数的函数式接口 解决缺乏基本类型函数式接口的问题 本笔记参考自: 《On Java 中文版》 函数式编程语言的一个特点就是其处理代码片段的简易性&am…...
【Ambari】银河麒麟V10 ARM64架构_安装Ambari2.7.6HDP3.3.1问题总结
🍁 博主 "开着拖拉机回家"带您 Go to New World.✨🍁 🦄 个人主页——🎐开着拖拉机回家_大数据运维-CSDN博客 🎐✨🍁 🪁🍁 希望本文能够给您带来一定的帮助🌸文…...

李宏毅机器学习第一课(结尾附作业模型详细分析)
机器学习就是让机器找一个函数f,这个函数f是通过计算机找出来的 如果参数少的话,我们可以使用暴搜,但是如果参数特别多的话,我们就要使用Gradient Descent Regression (输出的是一个scalar数值) Classification (在…...

对日项目工作总结
从18年8月到23年中秋节,目前已经入职主营对日车载项目的公司满5年了,一般来说,在一家公司工作工作超过3年,如果是在比较大型以及流程规范的公司,那么该公司的工作流程,工作思维会深深地烙印在该员工的脑海中…...

设计模式探索:从理论到实践的编码示例 (软件设计师笔记)
😀前言 设计模式,作为软件工程领域的核心概念之一,向我们展示了开发过程中面对的典型问题的经典解决方案。这些模式不仅帮助开发者创建更加结构化、模块化和可维护的代码,而且也促进了代码的复用性。通过这篇文章,我们…...
【内网穿透】在Ubuntu搭建Web小游戏网站,并将其发布到公网访问
目录 前言 1. 本地环境服务搭建 2. 局域网测试访问 3. 内网穿透 3.1 ubuntu本地安装cpolar 3.2 创建隧道 3.3 测试公网访问 4. 配置固定二级子域名 4.1 保留一个二级子域名 4.2 配置二级子域名 4.3 测试访问公网固定二级子域名 前言 网:我们通常说的是互…...

在cesuim上展示二维模型
前提问题:在cesuim上展示二维模型 解决过程: 1.获取或定义所需变量 2.通过window.cesium.viewer.imageryLayers.addImageryProvider和new Cesium.UrlTemplateImageryProvider进行建模 3.传入url路径后拼接{z}/{x}/{y}.png 4.聚焦到此模型window.ces…...
c/c++中如何输入pi
标准的 C/C 语言中没有π这个符号及常量,一般在开发过程中是通过开发人员自己定义这个常量的,最常见的方式是使用宏定义: 方法1:#define pi 3.1415926 方法2:使用反三角函数const double pi acos(-1.0);...

python爬虫:JavaScript 混淆、逆向技术
Python爬虫在面对JavaScript混淆和逆向技术时可能会遇到一些挑战,因为JavaScript混淆技术和逆向技术可以有效地阻止爬虫对网站内容的正常抓取。以下是一些应对这些挑战的方法: 分析网页源代码:首先,尝试分析网页的源代码…...

Vue error:0308010C:digital envelope routines::unsupported
vue项目,npm run dev的时候出现:Error: error:0308010C:digital envelope routines::unsupported vue项目,npm run dev的时候出现:Error: error:0308010C:digital envelope routines::unsupported 这个是node的版本问题。我的nod…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

