队列的使用以及模拟实现(C++版本)
🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨
🐻强烈推荐优质专栏: 🍔🍟🌯C++的世界(持续更新中)
🐻推荐专栏1: 🍔🍟🌯C语言初阶
🐻推荐专栏2: 🍔🍟🌯C语言进阶
🔑个人信条: 🌵知行合一
🍉本篇简介:>:讲解队列的使用以及模拟实现
金句分享:
✨来日方长,未来是星辰大海般璀璨,✨
✨不必踌躇于过去的半亩方塘.✨
目录
- 一、队列的介绍
- 二、队列的使用
- 🍭练练手(用队列模拟栈)
- 三、队列的模拟实现:
- (1) 浅提一下双端队列`deque`
- (2) 模拟实现
一、队列的介绍
C++中的队列是一种容器,使用队列可以实现先进先出(FIFO)的数据结构。队列可以添加元素到队列的末尾,也可以从队列的开头删除元素。
队列作为容器适配器实现,容器适配器即将特定容器类封装作为其底层容器类,queue提供一组特定的
成员函数来访问其元素。元素从队尾入队列,从队头出队列。
C++中的队列通常使用STL库中的queue类实现。
队列的基本操作包括:
- push(element):将元素插入队列的末尾。
- pop():将队列的第一个元素删除。
- front():返回队列的第一个元素。
- back():返回队列的最后一个元素。
- empty():判断队列是否为空。
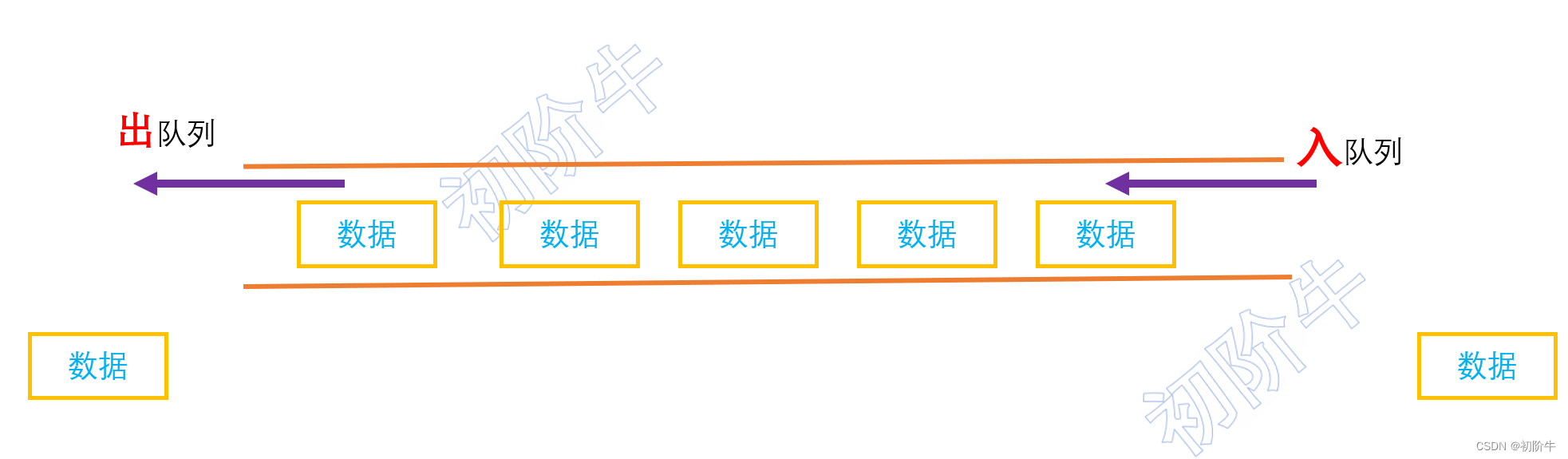
队列具有先进先出FIFO(First In First Out)
入队列:进行"插入"操作的一端称为队尾
出队列:进行"删除"操作的一端称为队头
二、队列的使用
文档链接

| 接口名 | 解释 |
|---|---|
| empty() | 判断是否为空队列 |
| size() | 返回队列中有效元素的个数 |
| front() | 返回队首元素的引用 |
| back() | 返回队尾元素的引用 |
| push() | 将新元素入队列 |
| emplace() | 将新元素入队列 |
| pop() | 将队首元素出队 |
相信大家对队列的基本操作十分简单,下面演示一下具体使用,使用十分简单,就不过分介绍了.
测试代码:
#include <iostream>
#include <queue>
using namespace std;void test1()
{queue<int> q1;//创建一个存储整形数据的队列q1.push(1); //入队列q1.push(2);q1.push(3);q1.emplace(4); //在stack使用时有详细介绍cout << "q1.front=" << q1.front() << endl; //取队头元素cout << "q1.back=" << q1.back() << endl; //取队尾元素//利用front的返回值,修改队首元素int& top = q1.front();top = 22;//利用back的返回值,修改队尾元素int& back = q1.back();top = -22;cout << endl;while (!q1.empty()) //只要队列不为空,就打印队头元素和出队列{cout << q1.front() << endl;q1.pop();//出队列}
}int main()
{test1();return 0;
}
运行结果:
q1.front=1
q1.back=4
22
2
3
4
🍭练练手(用队列模拟栈)
题目链接:
同样,在C语言阶段,我们已经"十分痛苦"的写过这道题,现在C++阶段,再来写要轻松很多了.
用队列实现栈(C语言版本)
C++实现版本:
class MyStack {
public:MyStack() {}void push(int x) {if (!(q1.empty() && q2.empty())) {//往空栈里面插入数据q1.push(x);}else q2.push(x);}int pop() {queue<int>* empty_q ;queue<int>* un_empty_q;if (q1.empty()) {//找到两个队列中的空队列empty_q = &q1;un_empty_q = &q2;}else {empty_q = &q2;un_empty_q = &q1;}while (un_empty_q->size() > 1) {//将非空队列除了最后一个元素以外,其他全部插入到另一个队列empty_q->push(un_empty_q->front());un_empty_q->pop();}int front = un_empty_q->front();un_empty_q->pop();//删除剩下的最后一个元素->return front;}int top() {int top;if (q1.empty()) {top = q2.back();}else top = q1.back();return top;}bool empty() {return q1.empty() && q2.empty();}
private:queue<int> q1;queue<int> q2;
};
三、队列的模拟实现:
(1) 浅提一下双端队列deque
在介绍队列的,模拟实现前,先介绍一下deque.
双端队列(Double-Ended Queue),是一种具有队列和栈的特点的数据结构。它允许从两端插入和删除元素,具有以下特点:
- 可以从队列两端进行插入和删除操作。
- 支持常数级别的访问和修改元素,即在队列头和尾进行操作的时间复杂度都为O(1)。
- 在中间进行操作时,性能较差,时间复杂度为O(n)。
是的,这个双端队列不仅支持头插头删,尾插尾删的同时,还支持随机访问.
那这不就意味着链表list和vector都被淘汰了吗?
这里就不过多介绍deque的底层了,我们可以暂时理解为,类似于链表,但是链接起来的是一个个数组,这样就实现了这些功能.
但是,他并不能代替链表list和vector.原因如下:
与vector比较
deque的优势是:头部插入和删除时,不需要搬移元素,效率特别高,而且在扩容时,也不
需要搬移大量的元素
劣势:但是它的访问需要计算,在大量访问元素的场景时,与vector比就落后了.
与list比较
优势:其底层是连续空间,空间利用率比较高,不需要存储额外字段。
缺点:deque有一个致命缺陷:不适合遍历,因为在遍历时,deque的迭代器要频繁的去检测其是否移动到某段小空间的边界,导致效率低下,而序列式场景中,可能需要经常遍历,因此在实际中,需要线性结构时,大多数情况下优先考虑vector和list,deque的应用并不多.
巧合的是,stack和queue都不需要访问中间的元素,访问头部数据效率还是很高的.
所以STL用deque作为stack和queue的底层数据结构再合适不过了.
(2) 模拟实现
队列也是一种容器适配器,我们底层采用deque实现还是很轻松的.

#pragma once
#include <iostream>
#include <deque>
using namespace std;namespace cjn
{template<class T, class Con = deque<T>>//默认采用deque进行复用class queue{public:queue(){}void push(const T& x){ //入队列元素相当于尾插_c.push_back(x);}void pop(){_c.pop_front(); //出队列是从队首元素出队,所以相当于头删}T& back(){ //返回队尾元素return _c.back();}const T& back()const{return _c.back();}T& front(){ //返回队首元素return _c.front();}const T& front()const{return _c.front();}size_t size()const{ //返回队列中有效元素的个数return _c.size();}bool empty()const{ //判断队列是否为空return _c.empty();}private:Con _c;};
}
相关文章:

队列的使用以及模拟实现(C++版本)
🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨ 🐻强烈推荐优质专栏: 🍔🍟🌯C的世界(持续更新中) 🐻推荐专栏1: 🍔🍟🌯C语言初阶 🐻推荐专栏2: 🍔…...
RV1126笔记四十一:RV1126移植LIVE555
若该文为原创文章,转载请注明原文出处。 RV1126的SDK有提供了一个librtsp.a封装好的RTSP推流库,但不开源,还有个确定延时长,所以想自己写一个RTSP的推流,但不想太麻烦,所以使用Live555。 记录下移植过程和测试结果。 live555需要用到的包有 openssl 和live555 一、 编…...
stable diffusion模型评价框架
GhostReview:全球第一套AI绘画ckpt评测框架代码 - 知乎大家好,我是_GhostInShell_,是全球AI绘画模型网站Civitai的All Time Highest Rated (全球历史最高评价) 第二名的GhostMix的作者。在上一篇文章,我主要探讨自己关于ckpt的发展方向的观点…...
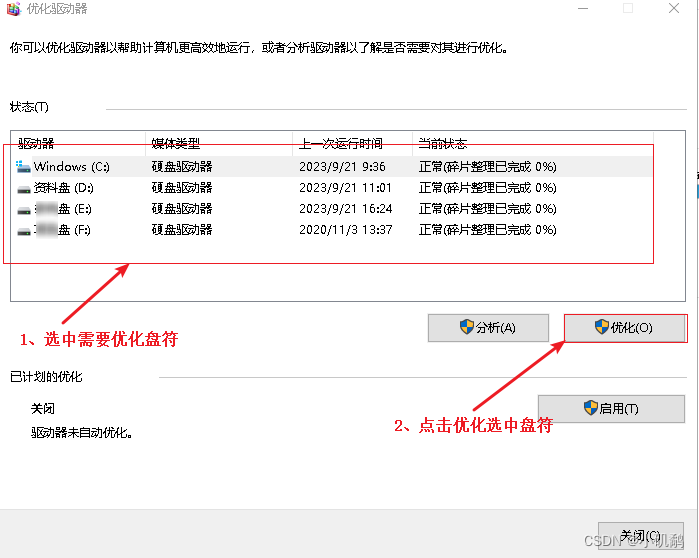
电脑开机慢问题的简单处理
电脑用久了,开机时间要10-20分钟特别慢,一下介绍两种简单有效处理方式,这两种方式经测试不会影响原系统软件的使用: 方式一:禁用非必要启动项【效果不是很明显】 利用360里面的优化加速禁用启动项【禁用启动项还有其…...

SpringMVC-Rest风格
一、简介 REST(Representational State Transfer),表现形式状态转换,它是一种软件架构风格 当我们想表示一个网络资源的时候,可以使用两种方式: 传统风格资源描述形式 http://localhost/user/getById?id1 查询id为1的用户信息…...

WebGL实现透明物体(α混合)
目录 α混合 如何实现α混合 1. 开启混合功能: 2. 指定混合函数 混合函数 gl.blendFunc()函数规范 可以指定给src_factor和dst_factor的常量 混合后颜色的计算公式 加法混合 半透明的三角形(LookAtBlendedTriangl…...

RecycleView刷新功能
RecycleView刷新某一个Item,或这某一个Item中某一个View。 这样的需求,在实际的开发中是很普遍的。 在数据变化后需要刷新列表。 刷新列表有三种方式: 前两种大家应该很熟,第三中会有点陌生。 那么这三种方式,有什…...
目标检测如何演变:从区域提议和 Haar 级联到零样本技术
目录 一、说明 二、目标检测路线图 2.1 路线图(一般) 2.2 路线图(更传统的方法) 2.3 路线图(深度学习方法) 2.4 对象检测指标的改进 三、传统检测方法 3.1 维奥拉-琼斯探测器 (2001) 3.2 HOG探测器…...

聊一聊国内大模型公司,大模型面试心得、经验、感受
有着过硬的技术却无处可用是不是很苦恼呢,大家在面试时是不是也积累了一些经验呢,本文详细总结了大佬在大模型面试时的一些经验及感悟,希望对大家面试找工作有所帮助。 2023年,大模型突然国内火了起来,笔者就面了一些…...

【分布式微服务】feign 异步调用获取不到ServletRequestAttributes
公司调用接口的时候使用feign,但是服务之间还是使用了鉴权,需要通过RequestInterceptor 去传递uuid 概念 OpenFeign是一个声明式的Web服务客户端,它使得编写HTTP客户端变得更简单。在使用OpenFeign进行异步调用时,你可以通过配置来实现。但是,如果你在配置或调用过程中遇…...

c#编程里面最复杂的技术问题有哪些
C#编程中最复杂的技术问题通常涉及高级主题和复杂的应用场景。以下是一些可能被认为是C#编程中最复杂的技术问题: 1. **多线程和并发编程:** 处理多线程和并发问题涉及到锁定、线程同步、死锁避免、线程安全性和性能优化等方面的知识。编写高效且线程安…...
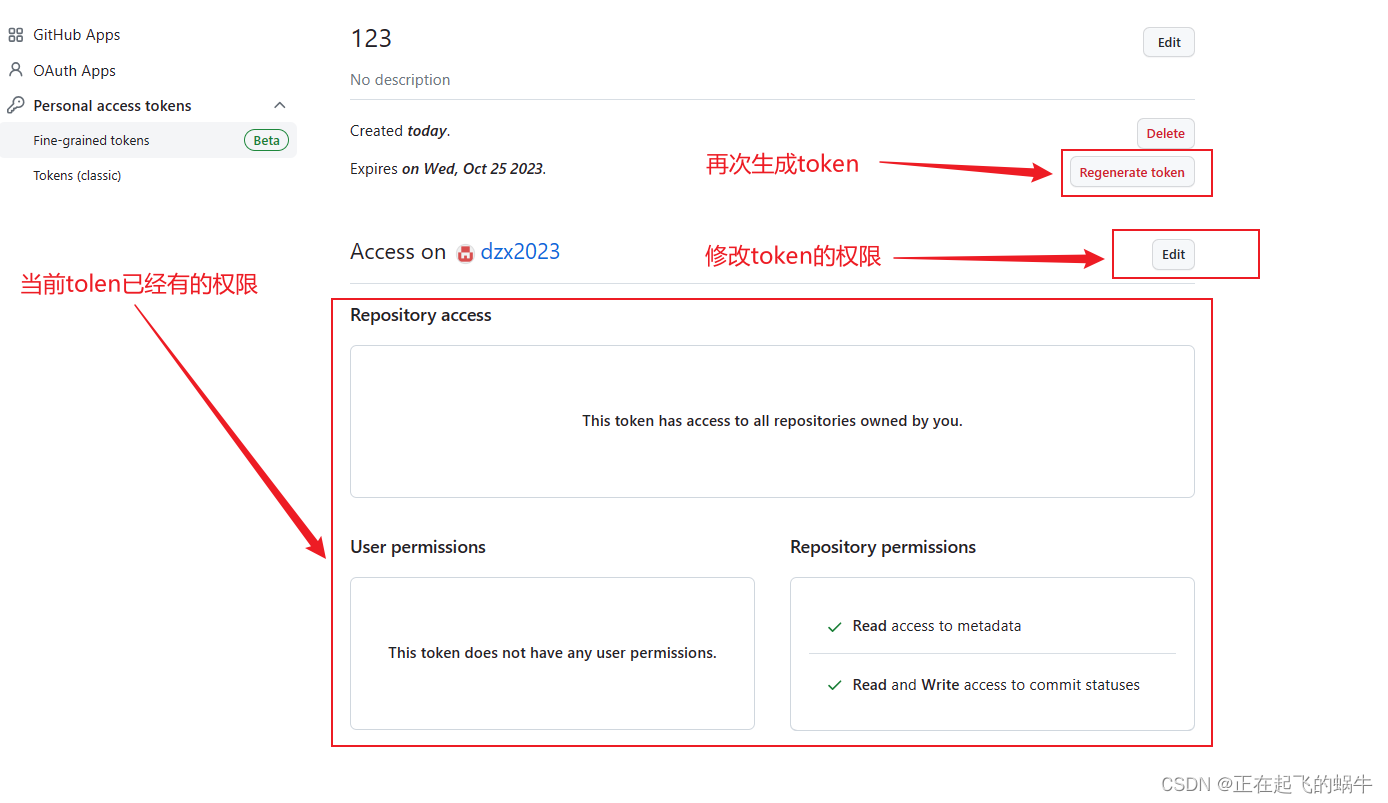
github代码提交过程详细介绍
1、下载github上面的代码 (1)在github网站上,找到想要下载的代码仓库界面,点击Code选项就可以看到仓库的git下载地址; (2)使用命令下载:git clone 地址; 2、配置本地git…...
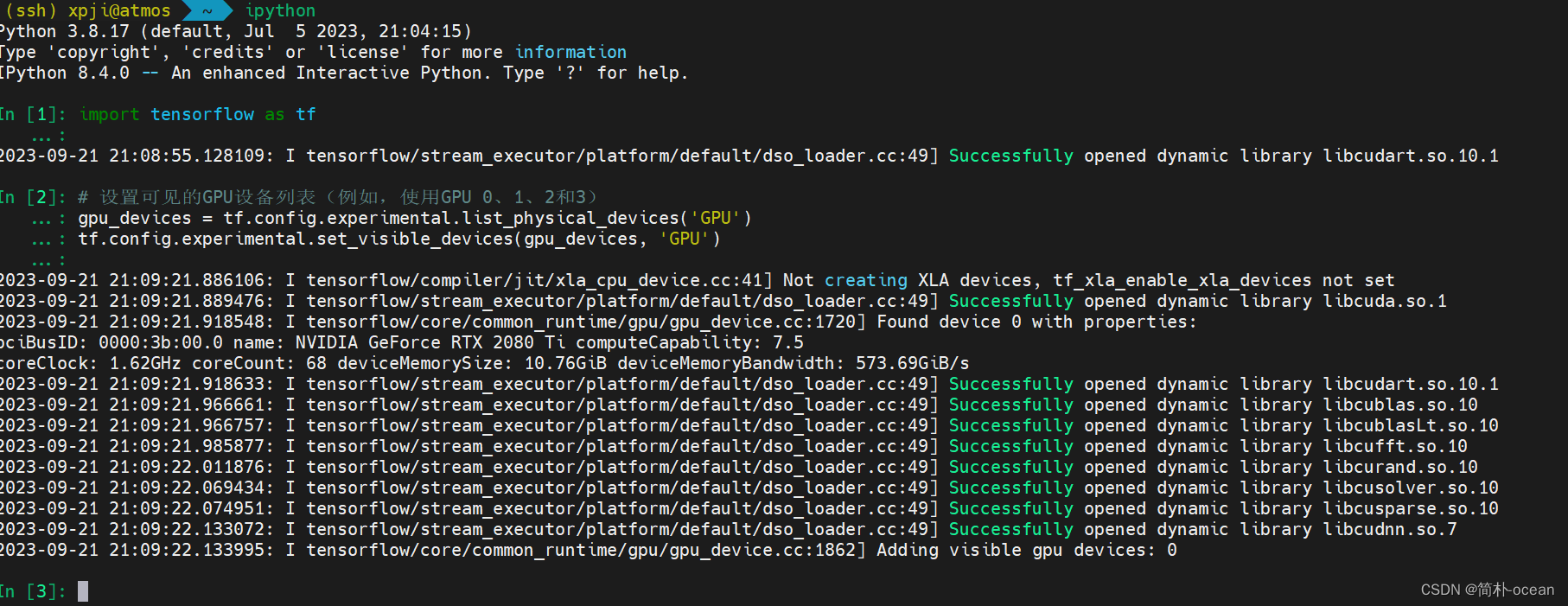
Linux -- 使用多张gpu卡进行深度学习任务(以tensorflow为例)
在linux系统上进行多gpu卡的深度学习任务 确保已安装最新的 TensorFlow GPU 版本。 import tensorflow as tf print("Num GPUs Available: ", len(tf.config.list_physical_devices(GPU)))1、确保你已经正确安装了tensorflow和相关的GPU驱动,这里可以通…...
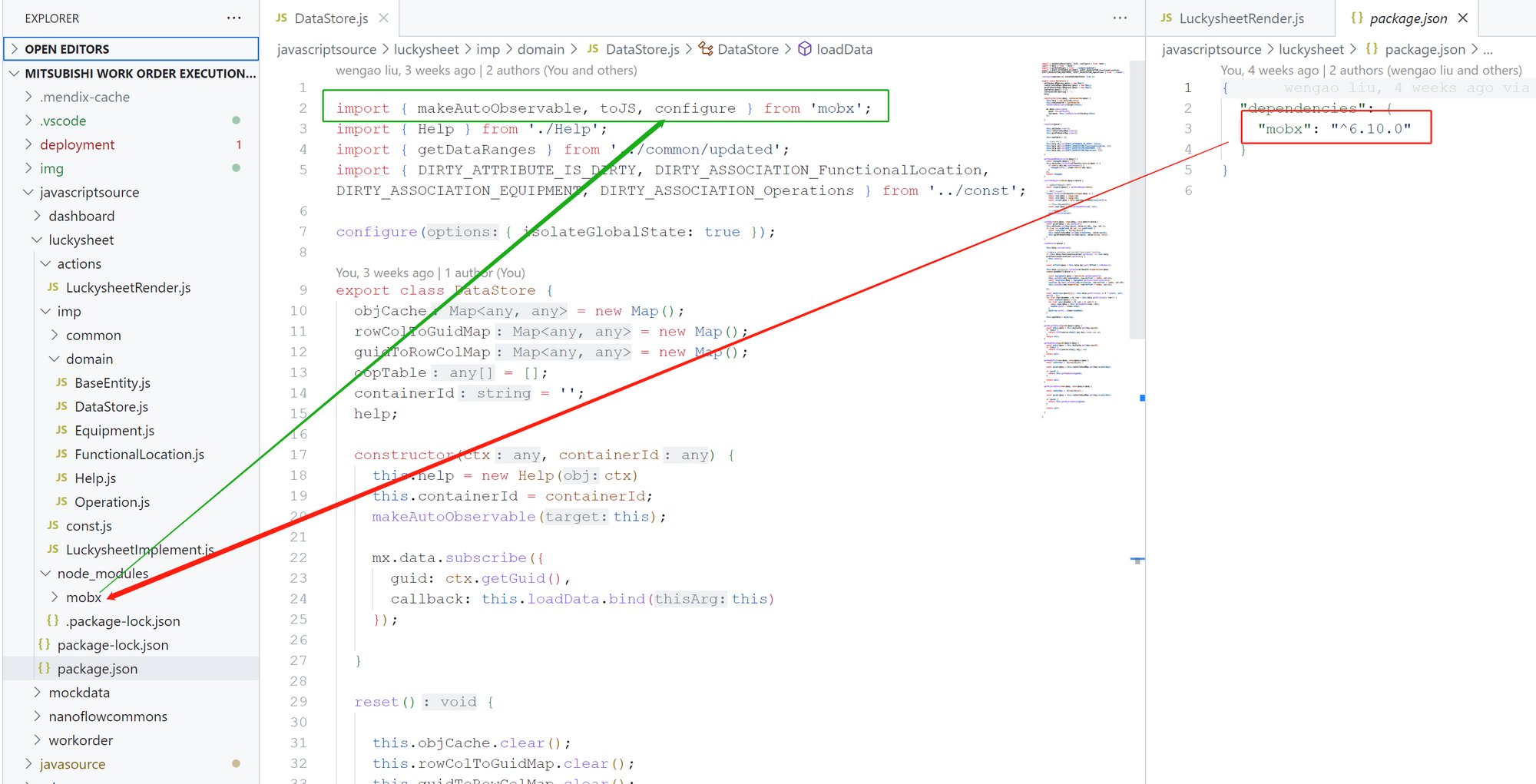
Mendix中的依赖管理:npm和Maven的应用
序言 在传统java开发项目中,我们可以利用maven来管理jar包依赖,但在mendix项目开发Custom Java Action时,由于目录结构有一些差异,我们需要自行配置。同样的,在mendix项目开发Custom JavaScript Action时,…...

自定义hooks之useLastState、useSafeState
自定义hooks之useLastState、useSafeState useLastState 在某些情况下,可能需要知道状态的历史值,例如,希望在状态变化时执行某些操作,但又需要访问上一个状态的值,以便进行比较或其他操作。自定义 React Hook 可以帮…...

前端判断: []+[], []+{}, {}+[], {}+{}
本质: 二元操作符规则 一般判断规则: 如果操作数是对象,则对象会转换为原始值如果其中一个操作数是字符串的话,另一个操作数也会转换成字符串,进行字符串拼接否则,两个操作数都将转换成数字或NaN,进行加法操作 转为原始数据类型的值的方法: Symbol.ToPrimitiveObject.protot…...
)
el-input-number/el-input 实现实时输入数字转换千分位(失焦时展示千分位)
el-input-number/el-input 实现实时输入数字转换千分位(失焦时展示千分位) 我把封装指令的代码放在了main.js,代码如下 // 金额展示千分位 Vue.directive("thousands", {inserted: function(el, binding) {// debugger// 获取input节点if (el.tagName.toLocaleUppe…...

一篇博客学会系列(2)—— C语言中的自定义类型 :结构体、位段、枚举、联合体
目录 前言 1、结构体 1.1、结构体类型的声明 1.2、特殊的结构体类型声明 1.3、结构体的自引用 1.4、结构体的定义和初始化 1.5、结构体成员变量的调用 1.6、结构体内存对齐 1.6.1、offsetof 1.6.2、结构体大小的计算 1.6.3、为什么存在内存对齐? 1.7、…...
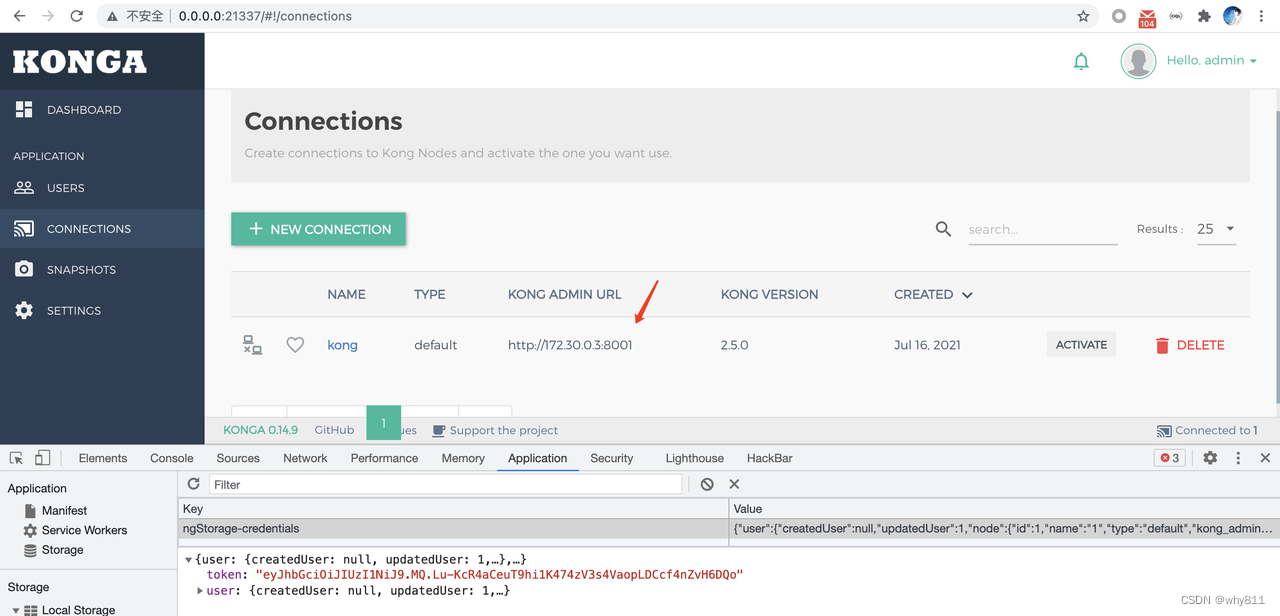
KongA 任意用户登录漏洞分析
KongA 简介 KongA 介绍 KongA 是 Kong 的一个 GUI 工具。GitHub 地址是 https://github.com/pantsel/konga 。 KongA 概述 KongA 带来的一个最大的便利就是可以很好地通过UI观察到现在 Kong 的所有的配置,并且可以对于管理 Kong 节点 漏洞成因 未设置TOKEN_SECRE…...
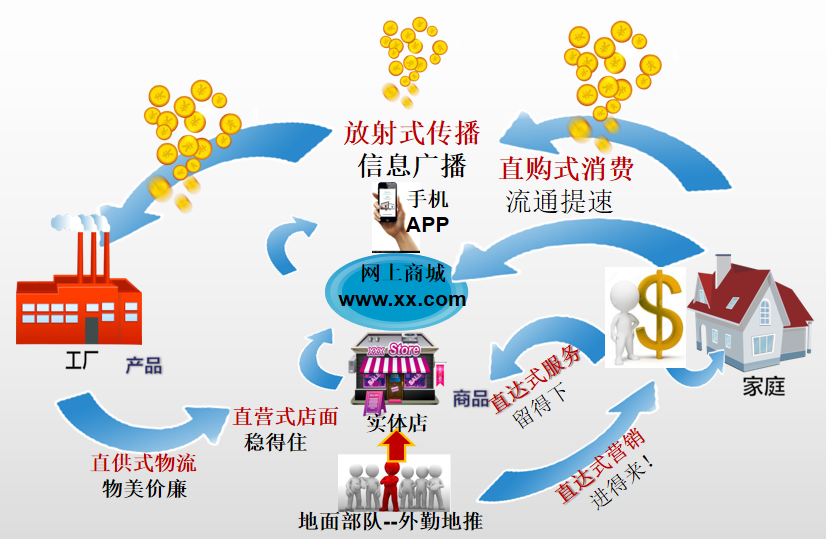
吉力宝:智能科技鞋品牌步力宝引领传统产业创新思维
在现代经济环境下,市场经济下产品的竞争非常的激烈,如果没有营销,产品很可能不被大众认可,酒香也怕巷子深,许多传统产业不得不面临前所未有的挑战。而为了冲出这个“巷子”,许多企业需要采用创新思维&#…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
