Linux -- 使用多张gpu卡进行深度学习任务(以tensorflow为例)
在linux系统上进行多gpu卡的深度学习任务
- 确保已安装最新的 TensorFlow GPU 版本。
import tensorflow as tf
print("Num GPUs Available: ", len(tf.config.list_physical_devices('GPU')))
- 1、确保你已经正确安装了tensorflow和相关的GPU驱动,这里可以通过在命令行输入
nvidia-smi来查看:
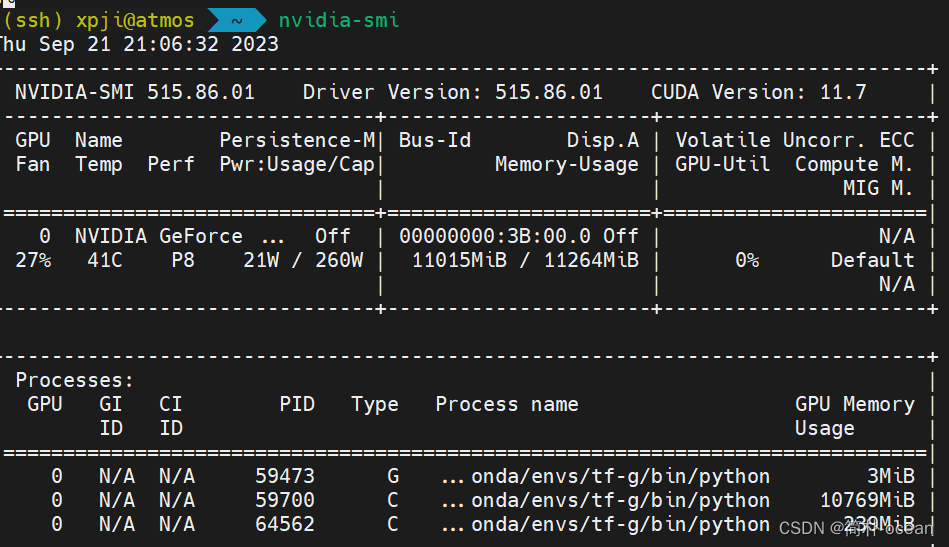
如果成功显示了类似上述的GPU信息和驱动版本信息,则说明NVIDIA驱动已经正确安装。
2、导入必要的库,设置可见的gpu设备列表:
import tensorflow as tf
# 设置可见的GPU设备列表(例如,使用GPU 0、1、2和3)
gpu_devices = tf.config.experimental.list_physical_devices('GPU')
tf.config.experimental.set_visible_devices(gpu_devices, 'GPU')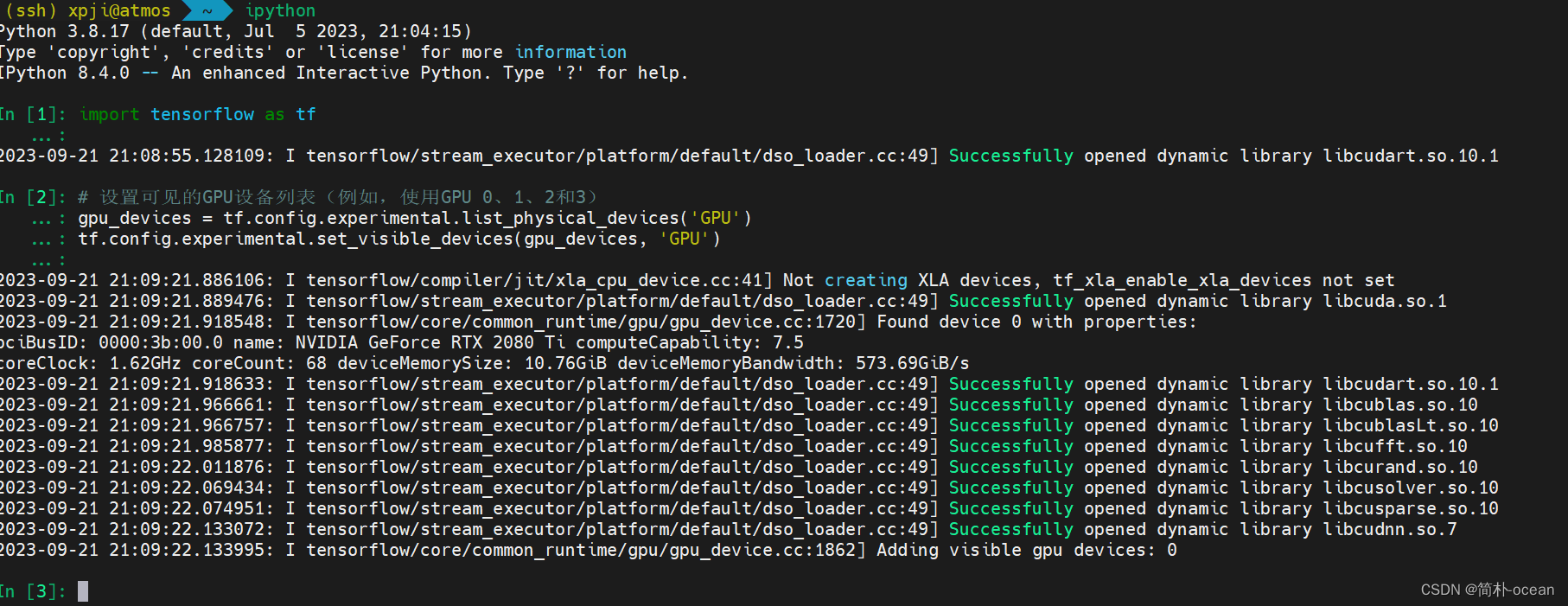
- 3、创建一个
MirroredStrategy对象,该对象将自动复制模型和数据到每个可见的GPU卡上:
strategy = tf.distribute.MirroredStrategy()
- 4、在
strategy范围内创建和训练模型:
with strategy.scope():# 创建和编译模型model = create_model()model.compile(...)# 加载数据train_dataset = load_train_data()test_dataset = load_test_data()# 训练模型model.fit(train_dataset, validation_data=test_dataset, ...)
以上,在MirroredStrategy范围内创建的模型将自动复制并分布到每个可见的GPU卡上,每个卡都将处理一部分数据。
使用多个 GPU 的最佳做法是使用 tf.distribute.Strategy
以下给出一个官网的简单示例:
tf.debugging.set_log_device_placement(True)
gpus = tf.config.list_logical_devices('GPU')
strategy = tf.distribute.MirroredStrategy(gpus)
with strategy.scope():inputs = tf.keras.layers.Input(shape=(1,))predictions = tf.keras.layers.Dense(1)(inputs)model = tf.keras.models.Model(inputs=inputs, outputs=predictions)model.compile(loss='mse',optimizer=tf.keras.optimizers.SGD(learning_rate=0.2))
当然,也有手动的放置方法:
tf.debugging.set_log_device_placement(True)gpus = tf.config.list_logical_devices('GPU')
if gpus:# Replicate your computation on multiple GPUsc = []for gpu in gpus:with tf.device(gpu.name):a = tf.constant([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])b = tf.constant([[1.0, 2.0], [3.0, 4.0], [5.0, 6.0]])c.append(tf.matmul(a, b))with tf.device('/CPU:0'):matmul_sum = tf.add_n(c)print(matmul_sum)
在tensorflow上使用gpu:https://www.tensorflow.org/guide/gpu?hl=zh-cn
相关文章:

Linux -- 使用多张gpu卡进行深度学习任务(以tensorflow为例)
在linux系统上进行多gpu卡的深度学习任务 确保已安装最新的 TensorFlow GPU 版本。 import tensorflow as tf print("Num GPUs Available: ", len(tf.config.list_physical_devices(GPU)))1、确保你已经正确安装了tensorflow和相关的GPU驱动,这里可以通…...
Mendix中的依赖管理:npm和Maven的应用
序言 在传统java开发项目中,我们可以利用maven来管理jar包依赖,但在mendix项目开发Custom Java Action时,由于目录结构有一些差异,我们需要自行配置。同样的,在mendix项目开发Custom JavaScript Action时,…...

自定义hooks之useLastState、useSafeState
自定义hooks之useLastState、useSafeState useLastState 在某些情况下,可能需要知道状态的历史值,例如,希望在状态变化时执行某些操作,但又需要访问上一个状态的值,以便进行比较或其他操作。自定义 React Hook 可以帮…...

前端判断: []+[], []+{}, {}+[], {}+{}
本质: 二元操作符规则 一般判断规则: 如果操作数是对象,则对象会转换为原始值如果其中一个操作数是字符串的话,另一个操作数也会转换成字符串,进行字符串拼接否则,两个操作数都将转换成数字或NaN,进行加法操作 转为原始数据类型的值的方法: Symbol.ToPrimitiveObject.protot…...
)
el-input-number/el-input 实现实时输入数字转换千分位(失焦时展示千分位)
el-input-number/el-input 实现实时输入数字转换千分位(失焦时展示千分位) 我把封装指令的代码放在了main.js,代码如下 // 金额展示千分位 Vue.directive("thousands", {inserted: function(el, binding) {// debugger// 获取input节点if (el.tagName.toLocaleUppe…...

一篇博客学会系列(2)—— C语言中的自定义类型 :结构体、位段、枚举、联合体
目录 前言 1、结构体 1.1、结构体类型的声明 1.2、特殊的结构体类型声明 1.3、结构体的自引用 1.4、结构体的定义和初始化 1.5、结构体成员变量的调用 1.6、结构体内存对齐 1.6.1、offsetof 1.6.2、结构体大小的计算 1.6.3、为什么存在内存对齐? 1.7、…...
KongA 任意用户登录漏洞分析
KongA 简介 KongA 介绍 KongA 是 Kong 的一个 GUI 工具。GitHub 地址是 https://github.com/pantsel/konga 。 KongA 概述 KongA 带来的一个最大的便利就是可以很好地通过UI观察到现在 Kong 的所有的配置,并且可以对于管理 Kong 节点 漏洞成因 未设置TOKEN_SECRE…...
吉力宝:智能科技鞋品牌步力宝引领传统产业创新思维
在现代经济环境下,市场经济下产品的竞争非常的激烈,如果没有营销,产品很可能不被大众认可,酒香也怕巷子深,许多传统产业不得不面临前所未有的挑战。而为了冲出这个“巷子”,许多企业需要采用创新思维&#…...
)
【IPC 通信】信号处理接口 Signal API(1)
收发信号思想是 Linux 程序设计特性之一,一个信号可以认为是一种软中断,通过用来向进程通知异步事件。 本文讲述的 信号处理内容源自 Linux man。本文主要对各 API 进行详细介绍,从而更好的理解信号编程。 信号概述 遵循 POSIX.1,…...
使用GDIView排查GDI对象泄漏导致的程序UI界面绘制异常问题
目录 1、问题说明 2、初步分析 3、查看任务管理器,并使用GDIView工具分析 4、GDIView可能对Win10兼容性不好,显示的GDI对象个数不太准确 5、采用历史版本比对法,确定初次出现问题的时间点,并查看前一天的代码修改记录 6、将…...

蓝桥等考Python组别一级001
第一部分:选择题 1、Python L1 (15分) 下面哪个不是Python的编程环境?( ) Python在线编程IDLEPyCharmScratch正确答案:D 2、Python L1(15分) 世界上第一台通用电子计算机ENIAC是在( )诞生的。 美国英国日本德国正确答案:A 3、Python L1(20分) 关于P…...

Unity之Hololens2开发 如何接入的MRTK OpenXR Plugin
一.前言 什么是Hololens? Hololens是由微软开发的一款混合现实头戴式设备,它将虚拟内容与现实世界相结合,为用户提供了沉浸式的AR体验。Hololens通过内置的传感器和摄像头,能够感知用户的环境,并在用户的视野中显示虚拟对象。这使得用户可以与虚拟内容进行互动,将数字信…...
Ubuntu系统Linux内核安装和使用
安装: 检查树莓派Linux版本,我的是6.1 uname -r 内核下载链接: Raspberry Pi GitHub 找对应版本下载 导入之后,解压安装即可 unzip linux-rpi-6.1.y.zip 其他内容 treee 指令安装 sudo apt-get install tree 使用这…...
”)
数学术语之源——群同态的“核(kernel)”
1. “kernel”这个术语在群论中的起源 Ivar Fredholm 在 1903 年的第27期Acta Math 数学学报发表的一篇关于“积分方程(INTEGRAL EQUATIONS)”的著名论文(“关于一类函数方程(Sur une classe des quations fonctionnelles)”)中使用了法语“noyau(核)”(365-390页)。 David …...
defcon-quals 2023 crackme.tscript.dso wp
将dso文件放到data/ExampleModule目录下,编辑ExampleModule.tscript文件 function ExampleModule::onCreate(%this) { trace(true); exec("./crackme"); __main("aaaaaaaa"); quit(); } 然后点击主目录下的Torque3D-debug.bat就可以在生成的c…...

前端开发 vs. 后端开发:编程之路的选择
文章目录 前端开发:用户界面的创造者1. HTML/CSS/JavaScript:2. 用户体验设计:3. 响应式设计:4. 前端框架: 后端开发:数据和逻辑的构建者1. 服务器端编程:2. 数据库:3. 安全性&#…...

算法练习4——删除有序数组中的重复项 II
LeetCode 80 删除有序数组中的重复项 II 给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。 不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 …...
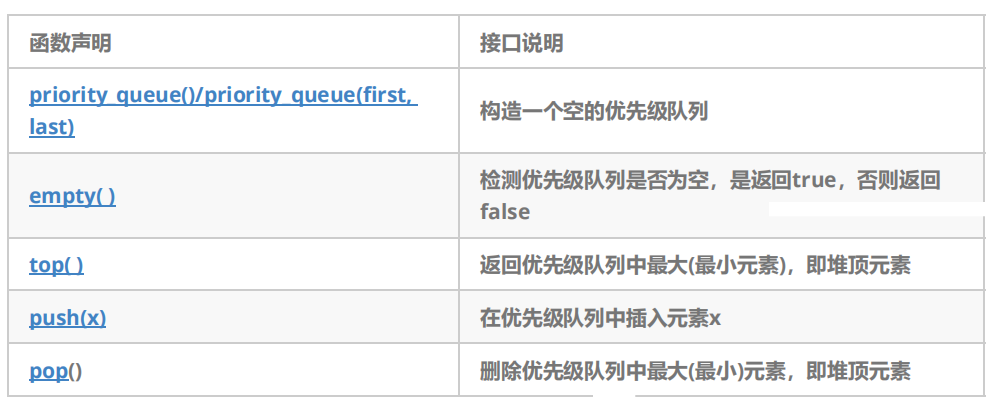
【C++进阶(六)】STL大法--栈和队列深度剖析优先级队列适配器原理
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:C从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习C 🔝🔝 栈和队列 1. 前言2. 栈和队列的接口函数熟悉3. …...

linux opensuse使用mtk烧录工具flashtool
环境 linux发行版:opensuse leap 15.5 工具:SP_Flash_Tool_Selector_exe_Linux_v1.2316.00.100.rar 或其他版本 目标:mtk设备 下载链接 https://download.csdn.net/download/zmlovelx/88382784 或网络搜索。 使用 opensuse可直接解压后使…...
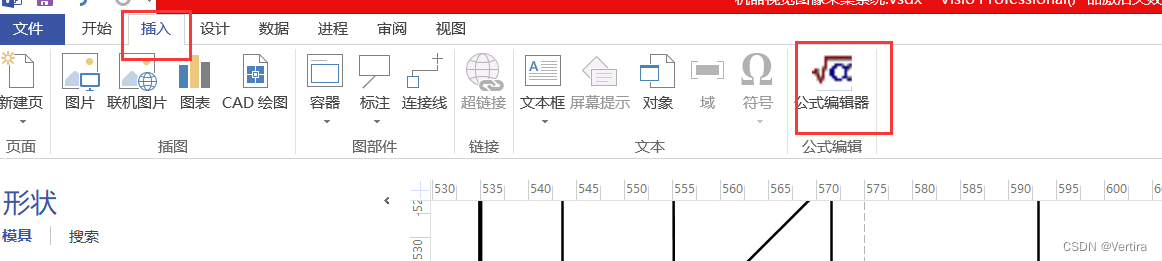
Visio如何对文本打下标、上标,以及插入公式编辑器等问题(已解决)
解决这个问题的本质问题,就是在Visio中插入公式编辑器(这不是visio的常用命令,需要添加)。 打开Visio--》文件--选项 点击选项,弹出对话框。在自定义功能区中,点击 常用命令,在下拉选项中&#…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...
