C++友元函数和友元类
友元介绍
类的友元函数是定义在类外部,但有权访问类的所有私有(private)成员和保护(protected)成员。尽管友元函数的原型有在类的定义中出现过,但是友元函数并不是成员函数。
友元可以是一个函数,该函数被称为友元函数;友元也可以是一个类,该类被称为友元类,在这种情况下,整个类及其所有成员都是友元。
如果要声明函数为一个类的友元,需要在类定义中该函数原型前使用关键字 friend,如下所示:
class Box
{double width;
public:double length;friend void printWidth( Box box );void setWidth( double wid );
};
声明类 ClassTwo 的所有成员函数作为类 ClassOne 的友元,需要在类 ClassOne 的定义中放置如下声明:
friend class ClassTwo;
友元函数应用代码示例:
#include <iostream>using namespace std;class Box
{double width;
public:friend void printWidth( Box box );void setWidth( double wid );
};// 成员函数定义
void Box::setWidth( double wid )
{width = wid;
}// 请注意:printWidth() 不是任何类的成员函数
void printWidth( Box box )
{/* 因为 printWidth() 是 Box 的友元,它可以直接访问该类的任何成员 */cout << "Width of box : " << box.width <<endl;
}// 程序的主函数
int main( )
{Box box;// 使用成员函数设置宽度box.setWidth(10.0);// 使用友元函数输出宽度printWidth( box );return 0;
}编译执行结果:
Width of box : 10
友元类应用代码示例:
#include <iostream>using namespace std;class Box
{double width;
public:friend void printWidth(Box box);friend class BigBox;void setWidth(double wid);
};class BigBox
{
public :void Print(int width, Box &box){// BigBox是Box的友元类,它可以直接访问Box类的任何成员box.setWidth(width);cout << "Width of box : " << box.width << endl;}
};// 成员函数定义
void Box::setWidth(double wid)
{width = wid;
}// 请注意:printWidth() 不是任何类的成员函数
void printWidth(Box box)
{/* 因为 printWidth() 是 Box 的友元,它可以直接访问该类的任何成员 */cout << "Width of box : " << box.width << endl;
}// 程序的主函数
int main()
{Box box;BigBox big;// 使用成员函数设置宽度box.setWidth(10.0);// 使用友元函数输出宽度printWidth(box);// 使用友元类中的方法设置宽度big.Print(20, box);getchar();return 0;
}编译执行结果
相关文章:

C++友元函数和友元类
友元介绍 类的友元函数是定义在类外部,但有权访问类的所有私有(private)成员和保护(protected)成员。尽管友元函数的原型有在类的定义中出现过,但是友元函数并不是成员函数。 友元可以是一个函数…...
特斯拉——使用人工智能制造智能汽车
特斯拉(Tesla)是电动汽车开发和推广的先驱。特斯拉对自动驾驶汽车的未来寄予厚望--实际上,每一辆特斯拉汽车都有可能通过软件升级成为自动驾驶汽车。该公司还生产和销售高级电池和太阳能电池板。 汽车的自动驾驶是按从1~5的等级划分的。自适应巡航控制和自动停车系…...

如何删除gitlab上多余的文件夹
无意间在提交代码时,包含了多余的 .idea 或者 __pychche__ 缓存文件夹等等,如何一次性删除呢? 实际上没有更好的办法,如果还没有合并,close 掉 MR就行了,重新提交。 如果已经合并了,就会留下记…...

computed和methods有什么区别
面试题:computed和methods有什么区别 标准而浅显的回答 在使用时,computed当做属性使用,而methods则当做方法调用computed可以具有getter和setter,因此可以赋值,而methods不行computed无法接收多个参数,而m…...
、聚集索引、二级索引(索引篇 二))
MySQL索引分类和操作(增删查)、聚集索引、二级索引(索引篇 二)
具体类型索引分类 分类主要作用特点主键索引(primary)针对于表中主键创建的索引默认自动创建, 只能有一个唯一索引(unique)避免同一个表中某数据列中的值重可以有多个常规索引最基本类型,可以加快查询速度可以有多个全文索引(fulltext)查找的是文本中的关键词&…...
(三)Python变量类型和运算符
所有的编程语言都支持变量,Python 也不例外。变量是编程的起点,程序需要将数据存储到变量中。 变量在 Python 内部是有类型的,比如 int、float 等,但是我们在编程时无需关注变量类型,所有的变量都无需提前声明&#x…...

vue三种import导入方式详解?
在Vue.js中,你可以使用三种不同的方式来导入模块或组件: 默认导入 (Default Import): 这种方式用于导入一个模块的默认导出(通常是一个组件或一个对象)。例如: import MyComponent from ./MyComponent.vue;…...

深入理解数据库视图
在数据库管理中,视图(View)是一种强大但常常被忽视的功能。它不仅可以简化复杂的查询操作,还可以提供更高层次的数据抽象和保护。 本文将详细解析视图的各个方面,并以《三国志》游戏的数据为例,给出实际应用场景。 文章目录 什么是视图?基本结构创建视图查看视图的定义…...
方法的作用~)
Java中@before和setup()方法的作用~
在Java中,setup()和Before同时使用的作用是在测试方法之前执行一些准备工作, setup()是JUnit中的一个方法,它通常被用来初始化测试对象和设置测试环境,它会在每个测试方法执行之前被调用,并且可以在多个测试方法中共享…...
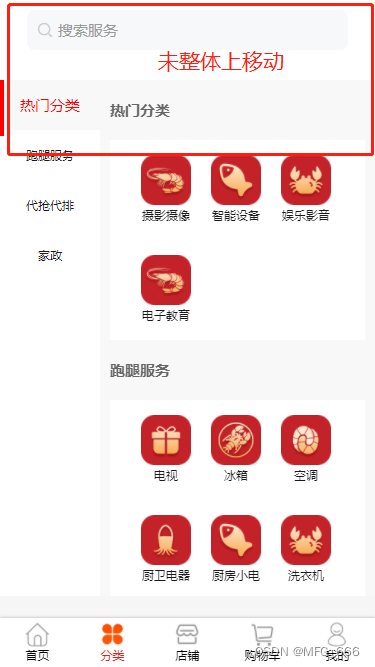
前端uniapp防止页面整体滑动页面顶部以上,设置固定想要固定区域宽高
解决:设置固定想要固定区域宽高 目录 未改前图未改样式改后图改后样式 未改前图 未改样式 .main {display: flex;flex-direction: row;// justify-content: space-between;width: 100vw;// 防止全部移动到上面位置!!!!…...

浮点型数字
1. 浮点型的定义 浮点型(floating-point)是一种表示实数的计算机数据类型,它可以表示有限小数、无限小数和近似值。浮点型的表示方法基于科学计数法,即一个实数可以表示为尾数(有效数字)和指数的乘积。 在…...

贝叶斯统计入门
贝叶斯统计入门 贝叶斯统计是一种以系统和数学严密的方式来推理不确定性的方法。它以18世纪的数学家和哲学家托马斯贝叶斯命名,他开发了一个定理,提供了一种在收集新数据时更新我们对假设的信念的方式。 在贝叶斯统计中,我们从一个先验概率分…...

织梦CMS采集插件-DEDE插件大全
在如今充满信息爆炸的互联网时代,维护一个具有吸引力和活力的网站或博客是一项具有挑战性的任务。对于那些使用织梦CMS建立网站的用户来说,如何持续不断地更新内容以吸引访问者成为了一个突出的问题。 什么是织梦CMS自动采集插件?这些插件是为…...
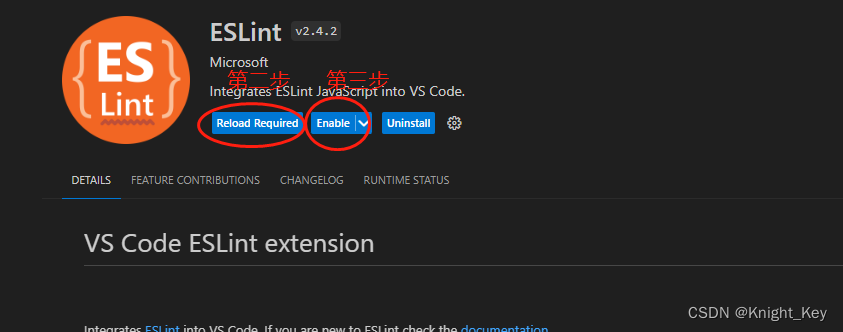
vuereact质检工具(eslint)安装使用总结
1、ESLint ESLint工具主要类似java中的checkStyle和findbugs,是检查代码样式和逻辑规范的工具。 1.1、ESLint安装流程 打开VSCode软件,打开扩展中心,下载ESLint插件 图1.1 点击后面的install按进行安装,如图1.2所示࿱…...

yolox相关
yolox YOLOXYOLOX-DarkNet53yolov3作为baseline输入端Strong data augmentationMosaic数据增强MixUp数据增强注意 BackboneNeckPrediction层Decoupled headDecoupled Head 细节 Anchor-freeAnchor Based方式Anchor Free方式标签分配初步筛选精细化筛选 SimOTASimOTA Other Back…...

递归专题训练详解(回溯,剪枝,深度优先)
1.汉诺塔问题 在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制: (1) 每次只能移动…...

JavaScript系列从入门到精通系列第七篇:JavaScrip当中的运算符,主要涉及JavaScript当中的六大数据类型的四则运算
文章目录 前言 一:算数运算符 1:Number类型的四则运算 2:其他数据类型的四则运算 (一):加法运算 (二):减法运算 3:乘法运算 4:除法运算 5:取模运算 前言 运算符也叫操作符。…...
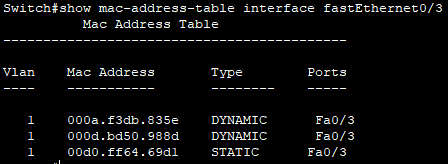
计算机网络 实验二 交换机的基本配置
实验二 交换机的基本配置 实验目的 • 掌握交换机的配置方式及切换命令; • 掌握交换机端口的基本配置; • 掌握交换机mac地址的查看与管理方法。 实验设备 以太网交换机一台服务器一台PC机五台配置电缆、网线若干 网络拓扑及IP地址分配 给计算…...

Tor网络的全面解析
一、Tor网络概述 Tor网络,即“洋葱路由器”(The Onion Router),是一种用于保护用户隐私、避免网络监控的开源软件,可以实现匿名访问互联网。 Tor网络通过多重加密和随机转发,将用户的流量从多个节点中进行…...

数据集笔记:2015上海地铁一卡通数据
数据地址:上海地铁数据_免费高速下载|百度网盘-分享无限制 (baidu.com) 数据介绍 上海2015年几天的地铁一卡通出入站信息 卡号、交易日期、交易时间、公交线路/地铁站点中文名称、行业名称(公交、地铁、出租、轮渡、PR停车场)、交易金额、交易性质(非优惠、优惠、…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...

STM32 低功耗设计全攻略:PWR 模块原理 + 睡眠 / 停止 / 待机模式实战(串口 + 红外 + RTC 应用全解析)
文章目录 PWRPWR(电源控制模块)核心功能 电源框图上电复位和掉电复位可编程电压监测器低功耗模式模式选择睡眠模式停止模式待机模式 修改主频一、准备工作二、修改主频的核心步骤:宏定义配置三、程序流程:时钟配置函数解析四、注意…...
