邓俊辉《数据结构》→ “2.6.5 二分查找(版本A)”之“成功查找长度”递推式推导
【问题描述】
邓俊辉的《数据结构(C++语言版)(第3版)》(ISBN:9787302330646)中,开始于第48页的“2.6.5 二分查找(版本A)”内容在第50页详述了“成功查找长度”的递推式,但此递推式乍一看令人费解。故为了说明问题,进行一些约定并详述如下:
● 既然是二分查找,所以给定的序列必定是有序的。
● 不失一般性,约定有序序列的长度 ,这样便可构建一个高度为 k 的满的二分查找树。
● 设 C(k) 表示高度为 k 的满的二分查找树中所有元素的查找长度总和。此时,问题就可以用递归方法求解。即 k 层的满二叉树,可以转化为左右两个 k-1 层的满二叉树。 依据邓俊辉《数据结构(C++语言版)(第3版)》(ISBN:9787302330646)中“2.6.5 二分查找(版本A)”的算法陈述,可知:
(1)第 k 层的查找长度为2(也即 );
(2)且稍加观察会发现左面的 k-1 层的子树所有元素的查找长度都会相对于以第 k-1 层为顶层时的查找长度多1(左子树共多 )。
(3)同样右面的 k-1 层的子树所有元素的查找长度都会相对于以第 k-1 层为顶层时的查找长度多2(右子树共多 )。
所以,根据递归算法的设计思想,需要把这些长度补上,共同构成 C(k)。

综上,可得 C(k) 的递推公式如下:
化简得:
若令,
则有:
故利用上文得出的 ,可进一步得出:
于是将 代入
可得:
从而可得平均查找长度为:
忽略掉低阶项、常数项、系数项,可得本版本的二分查找的平均查找长度的时间复杂度为:
【参考文献】
https://ask.csdn.net/questions/699067
https://www.bilibili.com/video/BV1C54y1L7JM/
https://www.bilibili.com/video/BV1C54y1L7JM/?p=76&vd_source=fea4f130ba05b1c873be1db0c639fc56
https://blog.csdn.net/hnjzsyjyj/article/details/133100051
https://blog.csdn.net/qq_33499861/article/details/105103708
相关文章:
邓俊辉《数据结构》→ “2.6.5 二分查找(版本A)”之“成功查找长度”递推式推导
【问题描述】 邓俊辉的《数据结构(C语言版)(第3版)》(ISBN:9787302330646)中,开始于第48页的“2.6.5 二分查找(版本A)”内容在第50页详述了“成功查找长度”的…...

Linux文件查找,别名,用户组综合练习
1.文件查看: 查看/etc/passwd文件的第5行 [rootserver ~]# head -5 /etc/passwd root:x:0:0:root:/root:/bin/bash bin:x:1:1:bin:/bin:/sbin/nologin daemon:x:2:2:daemon:/sbin:/sbin/nologin adm:x:3:4:adm:/var/adm:/sbin/nologin lp:x:4:7:lp:/var/spool/lpd:/sbin/nologi…...
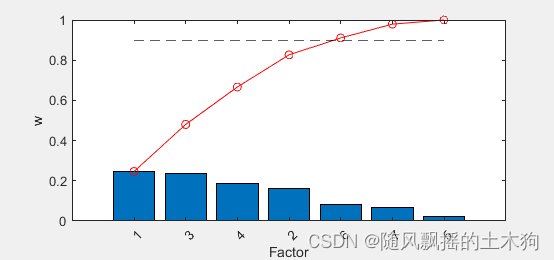
【MATLAB第77期】基于MATLAB代理模型算法的降维/特征排序/数据处理回归/分类问题MATLAB代码实现【更新中】
【MATLAB第77期】基于MATLAB代理模型算法的降维/特征排序/数据处理回归/分类问题MATLAB代码实现 本文介绍基于libsvm代理模型算法的特征排序方法合集,包括: 1.基于每个特征预测精度进行排序(libsvm代理模型) 2.基于相关系数corr的…...
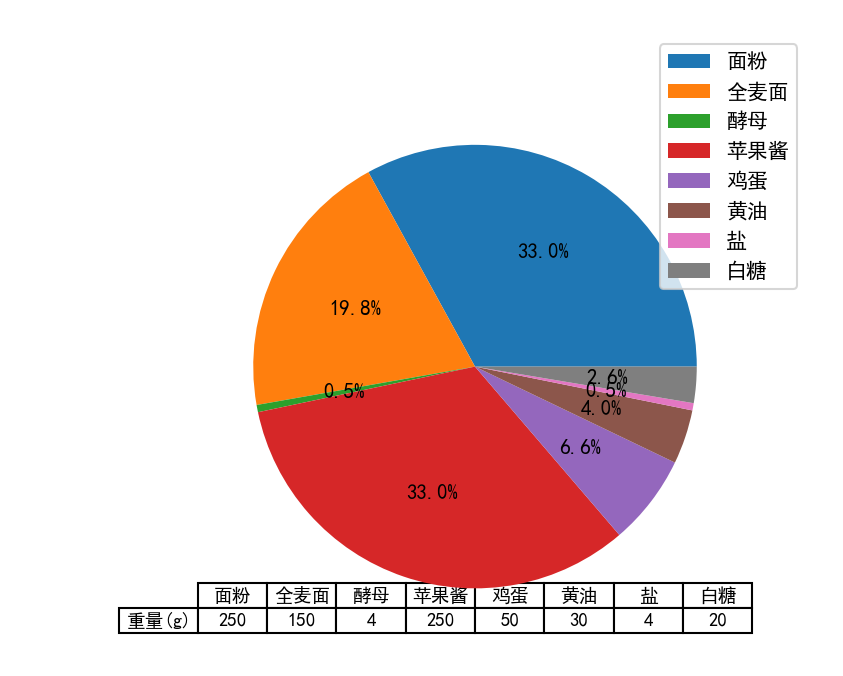
第三章 图标辅助元素的定制
第三章 图标辅助元素的定制 1.认识图表常用的辅助元素 图表的辅助元素是指除了根据数据绘制的图形之外的元素,常用的辅助元素包括坐标轴、标题、图例、网格、参考线、参考区域、注释文本和表格,它们都可以对图形进行补充说明。 上图中图表常用辅…...

【前端】ECMAScript6从入门到进阶
【前端】ECMAScript6从入门到进阶 1.ES6简介及环境搭建 1.1.ECMAScript 6简介 (1)ECMAScript 6是什么 ECMAScript 6.0(以下简称 ES6)是 JavaScript 语言的下一代标准,已经在2015年6月正式发布了。它的目标ÿ…...

Android Shape设置背景
设置背景时,经常这样 android:background“drawable/xxx” 。如果是纯色图片,可以考虑用 shape 替代。 shape 相比图片,减少资源占用,缩减APK体积。 开始使用。 <?xml version"1.0" encoding"utf-8"?…...

什么是GraphQL?它与传统的REST API有什么不同?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 什么是GraphQL?⭐ 与传统的REST API 的不同⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣…...

如何定时备份使用Docker构建的MySQL容器中的数据库
👨🏻💻 热爱摄影的程序员 👨🏻🎨 喜欢编码的设计师 🧕🏻 擅长设计的剪辑师 🧑🏻🏫 一位高冷无情的编码爱好者 大家好,我是 DevO…...

Java【手撕链表】LeetCode 143. “重排链表“, 图文详解思路分析 + 代码
文章目录 前言一、两数相加1, 题目2, 思路分析2,1 找到中间结点2.2, 逆序后半段链表2.3, 合并两个链表 3, 代码 前言 各位读者好, 我是小陈, 这是我的个人主页, 希望我的专栏能够帮助到你: 📕 JavaSE基础: 基础语法, 类和对象, 封装继承多态, 接口, 综合小练习图书管…...

C语言 cortex-A7核 按键中断 实验【重点】
一、KEY1 include/key.h #ifndef __KEY_H__ #define __KEY_H__#include "stm32mp1xx_rcc.h" #include "stm32mp1xx_gpio.h" #include "stm32mp1xx_exti.h" #include "stm32mp1xx_gic.h"//RCC/GPIO章节初始化 void hal_rcc_gpio_init…...

freertos中函数调用和启动第一个任务(栈相关!!!!!!)
本内容仅就一些较难理解的点讲解,请结合其它文章实用 在函数调用时,m3的处理器使用r0-r3共四个寄存器传参,其余的使用栈传参。 但是,如果传入的参数是全局变量,则不需传参,因为全局变量在函数内部是可见的…...
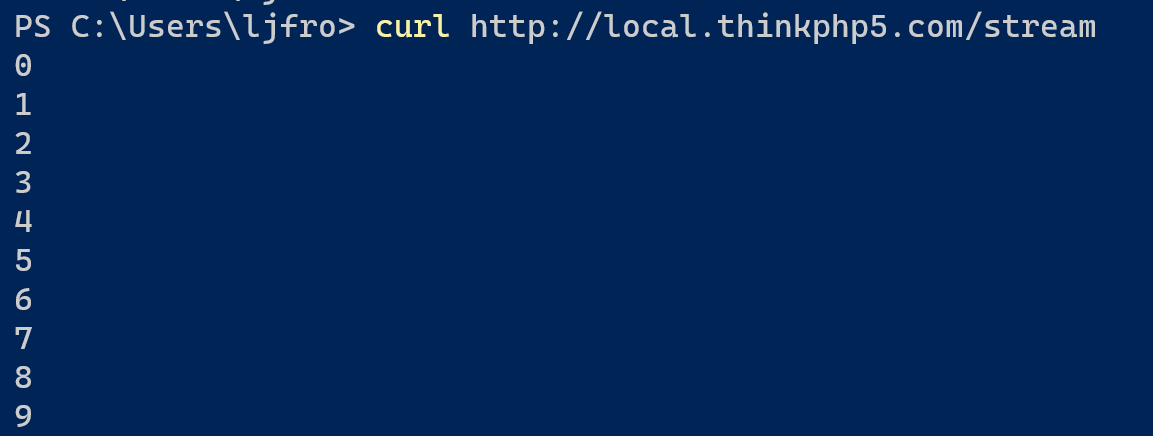
【PHP】如何关闭buffer实时输出内容到前端
前言 默认情况下,我们在PHP里使用echo等函数输出的内容,是不会马上发送给前端的,原因是有 buffer 的存在,buffer又分两处,一处是PHP本身的buffer,另一处是Nginx的buffer。只有当buffer满了之后,…...
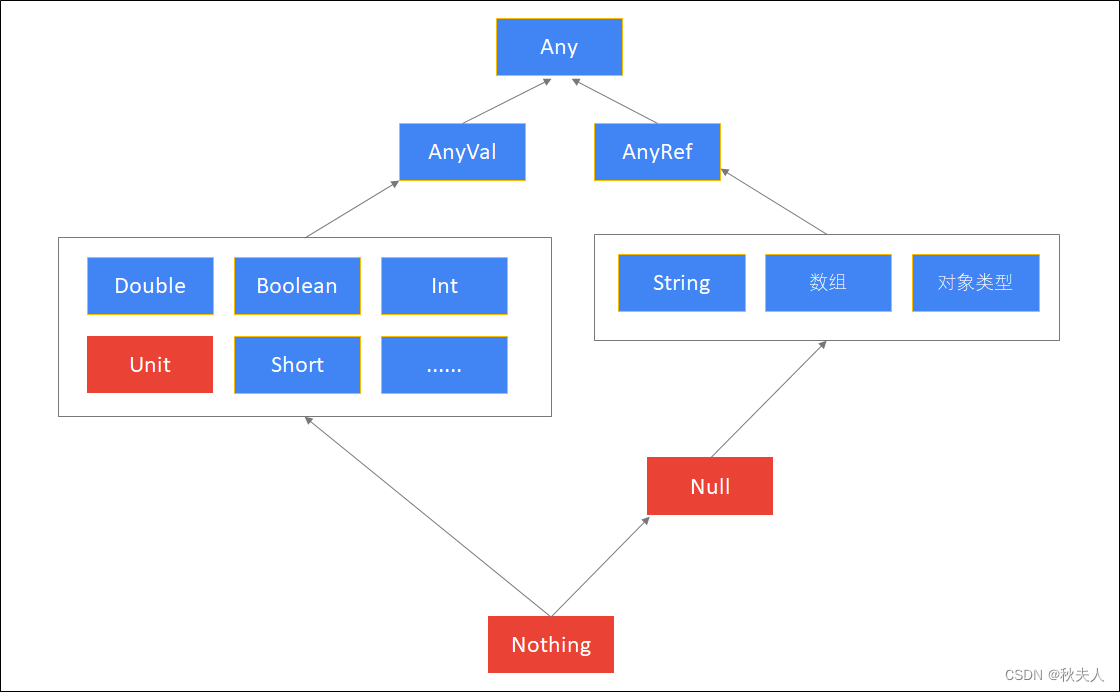
Scala第二章节
Scala第二章节 scala总目录 章节目标 掌握变量, 字符串的定义和使用掌握数据类型的划分和数据类型转换的内容掌握键盘录入功能理解Scala中的常量, 标识符相关内容 1. 输出语句和分号 1.1 输出语句 方式一: 换行输出 格式: println(里边写你要打印到控制台的数据);方式二…...

Spring修炼之路(2)依赖注入(DI)
一、概念 依赖注入(Dependency Injection,DI)。 测试pojo类 : Address.java 依赖 : 指Bean对象的创建依赖于容器 . Bean对象的依赖资源 . 注入 : 指Bean对象所依赖的资源 , 由容器来设置和装配 . 二、 注入方式 2.1构造器注入 我们在之前的案例已经…...
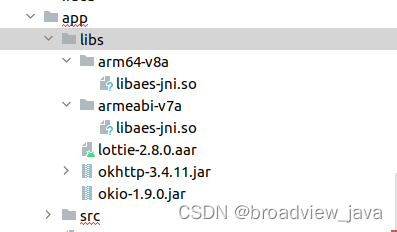
编写Android.mk / Android.bp 引用三方 jar 包,aar包,so 库
一.前言 在Android10之后,所有项目工程中,官方推荐使用Android.bp去编译构建,以前使用Android.mk构建的项目随着版本迭代升级,慢慢需要变更为Android.bp, 两者的语法都需要去了解并熟练使用。 笔者之前写过Android.mk的…...
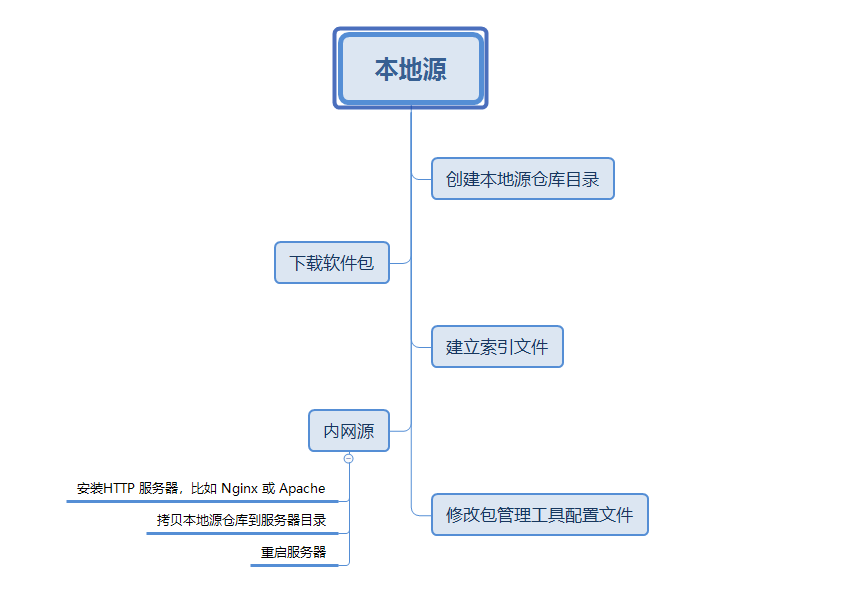
【kylin】【ubuntu】搭建本地源
文章目录 一、制作一个本地源仓库制作ubuntu本地仓库制作kylin本地源 二、制作内网源服务器ubuntu系统kylin系统 三、使用内网源ubuntukylin 一、制作一个本地源仓库 制作ubuntu本地仓库 首先需要构建一个本地仓库,用来存放软件包 mkdir -p /path/to/localname/pac…...

为什么 Go 语言 struct 要使用 tags
在 Go 语言中,struct 是一种常见的数据类型,它可以用来表示复杂的数据结构。在 struct 中,我们可以定义多个字段,每个字段可以有不同的类型和名称。 除了这些基本信息之外,Go 还提供了 struct tags,它可以用…...

WebGL笔记:WebGL中JS与GLSL ES 语言通信,着色器间的数据传输示例:用鼠标控制点位
用鼠标控制点位 <canvas id"canvas"></canvas><!-- 顶点着色器 --> <script id"vertexShader" type"x-shader/x-vertex">attribute vec4 a_Position;void main() {// 点位gl_Position a_Position;// 尺寸gl_PointSize…...
)
算法 主持人调度-(双指针+贪心)
牛客网: BM96 题目: 一个主持人只能参加一个活动,至少需要多少主持人 思路: 对start, end排序从小到大;初始化指针l, r 0, 0;start[r]< end[l]时需要累加人数同时r,否则l,r同时移动;直至不再满中l<n &&am…...
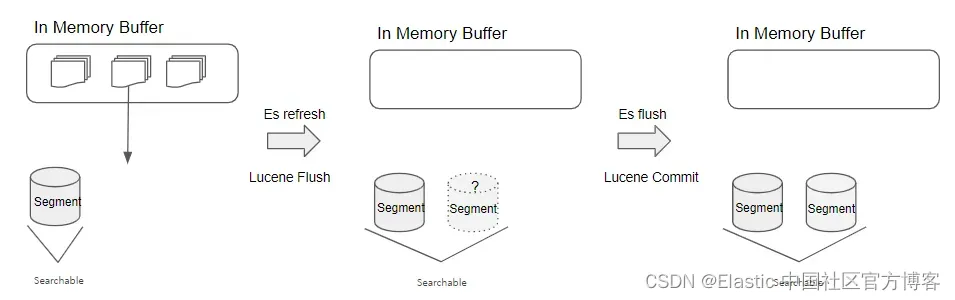
Elasticsearch 集群时的内部结构是怎样的?
Apache Lucene : Flush, Commit Elasticsearch 是一个基于 Apache Lucene 构建的搜索引擎。 它利用 Lucene 的倒排索引、查询处理和返回搜索结果等功能来执行搜索。 它还扩展了 Lucene 的功能,添加分布式处理功能以支持大型数据集的搜索。 让我们看一下 Apache Luc…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
