vuex的使用
1 vuex的使用
1 vuex的使用
store/index.js
-在Vue中实现集中式状态(数据)管理的一个Vue插件,对vue应用中多个组件的共享状态进行集中式
的管理(读/写),也是一种组件间通信的方式,且适用于任意组件间通信-使用步骤:1 新建store/index.jsimport Vue from 'vue'import Vuex from 'vuex'Vue.use(Vuex)export default new Vuex.Store({state: {num: 10},mutations: {add_mu(state, i) {state.num += i}},actions: {add(context, i) {// 逻辑判断,跟后端交互,通过后在做context.commit('add_mu', i)}},})2 在组件中使用变量拿值:this.$store.state.num 修改值:三种方式-直接:this.$store.state.num += 1-间接:this.$store.commit('add_mu',3)-间间接:this.$store.dispatch('add',10)3 任意组件都都可以使用,实现了组件间通信
组件
<template><div class="hello"><button @click="handleAdd">增加购物车</button></div>
</template><script>
export default {name: 'HelloWorld',props: {msg: String},methods: {handleAdd() {// 让状态管理器中:state的值加1// 方式1:直接操作,不好this.$store.state.num += 1// 方式2:先dispatch触发action的方法----》再commit触发mutations----》// 再mutations中修改statethis.$store.dispatch('add', 10)// 方式3:this.$store.commit('add_mut', 3)}}
}
</script>
相关文章:

vuex的使用
1 vuex的使用 1 vuex的使用 store/index.js -在Vue中实现集中式状态(数据)管理的一个Vue插件,对vue应用中多个组件的共享状态进行集中式 的管理(读/写),也是一种组件间通信的方式,且适用于任意…...
raw图片处理软件:DxO PhotoLab 6 mac中文版支持相机格式
DxO PhotoLab 6 mac是一款专业的RAW图片处理软件,适用于Mac操作系统。它具有先进的图像处理技术和直观易用的界面,可帮助用户轻松地将RAW格式的照片转换为高质量的JPEG或TIFF图像。 DxO PhotoLab 6支持多种相机品牌的RAW格式,包括佳能、尼康、…...

ReactPortals传送门
ReactPortals传送门 React Portals提供了一种将子节点渲染到父组件以外的DOM节点的解决方案,即允许将JSX作为children渲染至DOM的不同部分,最常见用例是子组件需要从视觉上脱离父容器,例如对话框、浮动工具栏、提示信息等。 描述 <div&…...
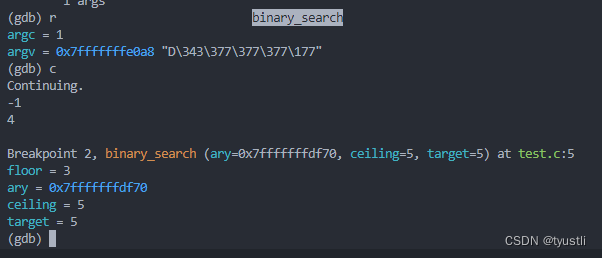
【GDB】 command 命令
GDB command 命令 语法 command 命令是一个很好用的调试命令,它配合断点使用,可以在指定的断点执行预先设置的命令 其语法为:command bread_id,这样会提示你输入你要执行的命令,以 end 结束。这个 bread_id 就是用 …...

1038 统计同成绩学生
输入样例: 10 60 75 90 55 75 99 82 90 75 50 3 75 90 88 输出样例: 3 2 0 solution #include <stdio.h> int main(){int n, d, k, hash[101] {0}, a[100000];scanf("%d", &n);for(int i 0; i < n; i){scanf("%d&quo…...

git报错:Failed to connect to 127.0.0.1 port 1080
Bug描述 由于在试了网上的这条命令 git config --global http.proxy socks5 127.0.0.1:1080 git config --global https.proxy socks5 127.0.0.1:1080git config --global http.proxy 127.0.0.1:1080 git config --global https.proxy 127.0.0.1:1080Bug描述:Faile…...
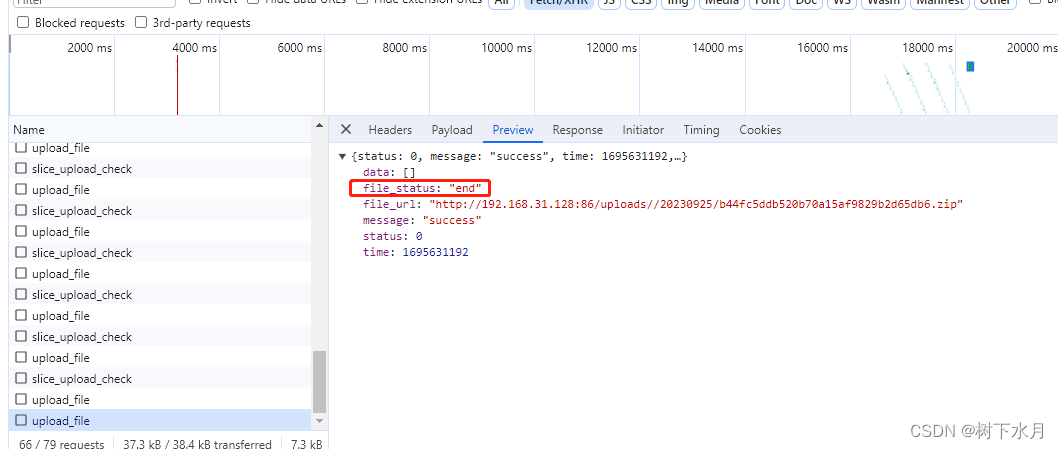
php eayswoole node axios crypto-js 实现大文件分片上传复盘
不啰嗦 直接上步骤 步骤1.开发环境配置 项目需要node.js 做前端支撑 官网下载地址: http://nodejs.cn/download/ 根据自己需要下载对应的版本,我下载的是windows系统64位的版本。 包下载好后 进行安装,安装步骤在此省略... 测试是否安装成功 …...
《Upload-Labs》01. Pass 1~13
Upload-Labs 索引前言Pass-01题解 Pass-02题解总结 Pass-03题解总结 Pass-04题解 Pass-05题解总结 Pass-06题解总结 Pass-07题解总结 Pass-08题解总结 Pass-09题解 Pass-10题解 Pass-11题解 Pass-12题解总结 Pass-13题解 靶场部署在 VMware - Win7。 靶场地址:https…...

v-for中的key
在Vue中,当使用v-for指令循环渲染元素时,添加:key是一个推荐做法,尤其是在循环的元素可能会被重新排序、添加或删除的情况下。 :key的作用是为每个循环的元素提供一个唯一的标识符,以便Vue能够跟踪和管理这些元素的状态。Vue使用…...
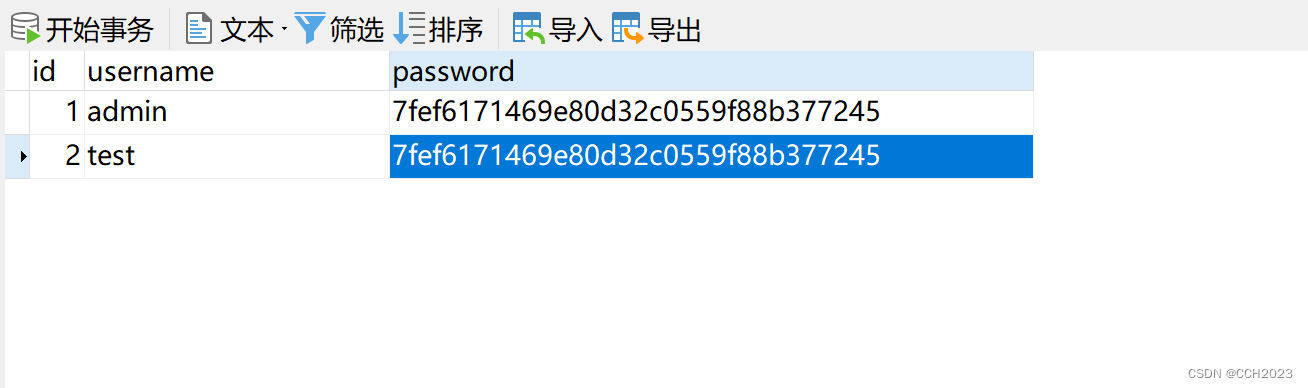
MySQL学习笔记17
MySQL权限管理grant: 权限说明: Table 6.2 Permissible Privileges for GRANT and REVOKE PrivilegeGrant Table ColumnContextALL [PRIVILEGES]Synonym for “all privileges”Server administrationALTERAlter_privTablesALTER ROUTINEAlter_routin…...

跨境电商建站:选择域名需要注意什么?
在跨境电商建站过程中,选择一个合适的域名至关重要,尤其是对于跨境电商独立站来说,它对未来的seo排名和品牌建设都有着重要影响。关于本文,我会先从域名的定义开始,到域名选择的重要性,再到如何选择一个完美…...

jupyterlab
1. 环境:linux 环境(基于ubuntu-fork 镜像实现) 2. pip install jupyter notebook 3. 编译jupyterlab源代码必须使用 node 14.21.3 高版本编译报错#下载 node 14.21.3 :wget https://nodejs.org/download/release/latest-v14.x/node-v14.21.…...
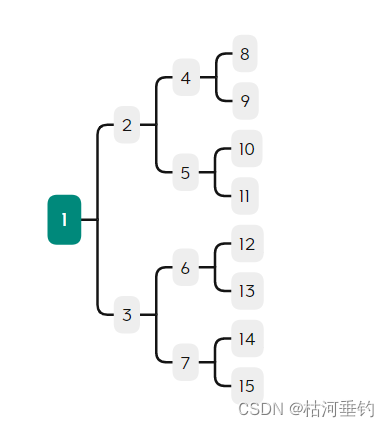
Oracle的递归公共表表达式
查询节点id为2的所有子节点的数据,包括向下级联 WITH T1 (id, parent_id, data) AS (SELECT id, parent_id, dataFROM nodesWHERE id 2UNION ALLSELECT t.id, t.parent_id, t.dataFROM nodes tJOIN T1 n ON t.parent_id n.id ) SELECT * FROM T1; --建表语句 C…...

解决antd vue ts v-model:value绑定Boolean布尔类型爆红但可以使用
没啥好写的,写点注意点把 前言:在 antd vue中需要用到对应的类型转换,v-model后面补一个value来表明类型,但这也是默认类型,并不是指定类型默认是 (property) value?: string | number | undefined 字符,…...
zblog插件大全-zblog免费插件
在当今数字化时代,拥有一个精彩的博客或网站已经成为许多人追求的目标。通过博客,我们可以分享知识、表达观点,甚至创造收入。然而,维持一个充满新鲜内容的博客却不是一件容易的事情。 ZBlog自动采集插件 什么是ZBlog自动采集插件…...

思科、华为、华三、锐捷网络设备巡检命令
下面为四种设备巡检命令,以便日常查阅: 华三 screen-length disable 取消分页 displayversion 查看版本 display clock 查看日期时钟 display fan 查看风扇状态 display power 查看电源信息 display cpu-usage 查看CPU利用率 display memory 查看…...

正则表达式贪婪模式和非贪婪模式
一、贪婪模式 贪婪模式表示尽可能多的匹配字符串,正则表达式六个量词元字符?、、*、{n}、{n,m}、{n,}默认是贪婪模式 接下来引入一个场景来分析说明 获取html a标签href属性的值 <a href"https://www.baidu.com/" attr"abc"></a>…...

借助 ControlNet 生成艺术二维码 – 基于 Stable Diffusion 的 AI 绘画方案
背景介绍 在过去的数月中,亚马逊云科技已经推出了多篇博文,来介绍如何在亚马逊云科技上部署 Stable Diffusion,或是如何结合 Amazon SageMaker 与 Stable Diffusion 进行模型训练和推理任务。 为了帮助客户快速、安全地在亚马逊云科技上构建、…...
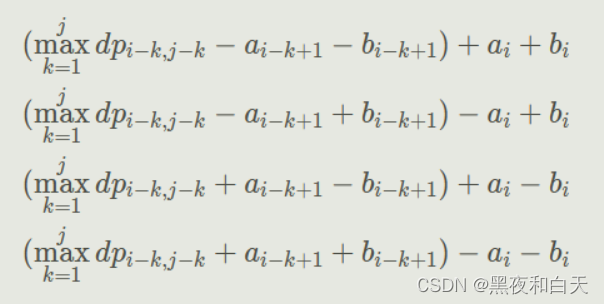
Codeforces Round 892 (Div. 2) - E. Maximum Monogonosity 思维dp 详细解析
题目链接 好久没有写题了复健一下qwq 题目大意 解题思路 这题目还挺妙的 首先考虑比较正常的dp, d p [ i ] [ j ] dp[i][j] dp[i][j] 为前 i i i的长度选 j j j个长度的最大价值,那么转移方程是: 图片来自:图片来源 但是这个是 …...

R语言中的数据重塑
文章目录 介绍reshape2::melt()的用法实例 reshape2::dcast()的用法实例 tidyr::gather()的用法tidyr::spread()的用法 介绍 tidyverse系列包中的函数操作都是针对简洁数据框进行的,对于不是简洁的数据,实现需要进行数据重塑。数据重塑主要包括长宽表的…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
