Codeforces Round 892 (Div. 2) - E. Maximum Monogonosity 思维dp 详细解析
题目链接
好久没有写题了复健一下qwq
题目大意

解题思路
这题目还挺妙的
首先考虑比较正常的dp, d p [ i ] [ j ] dp[i][j] dp[i][j] 为前 i i i的长度选 j j j个长度的最大价值,那么转移方程是:
图片来自:图片来源
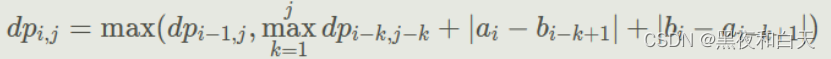
但是这个是 O ( n k 2 ) O(nk^2) O(nk2)无法通过把绝对值展开进行讨论
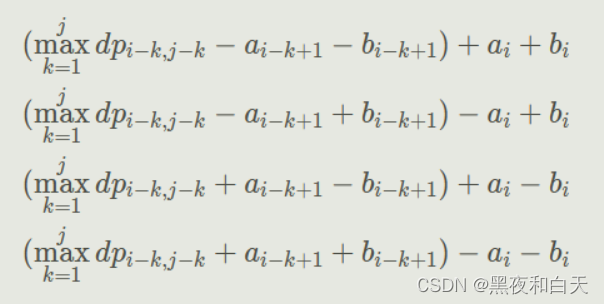
- 我们可以看到 d p [ i ] [ j ] dp[i][j] dp[i][j]其实都是由对角线上的 d p dp dp值 + + +几个 a a a, b b b的计算,那么我们可以把前面的部分用新的数组维护起来因为都是对角上的数值那么 i − j i-j i−j是固定值那么就是 f [ 0 / 1 / 2 / 3 ] [ i − j ] f[0/1/2/3][i-j] f[0/1/2/3][i−j]里面取最大值 + + +后缀部分
- 然后因为这个虽然是对角线的上值的前 k k k里面的最大值,但是其实 d p [ i ] [ j ] > d p [ i − 1 ] [ j − 1 ] dp[i][j]>dp[i-1][j-1] dp[i][j]>dp[i−1][j−1]是一定成立的所以 f [ 0 / 1 / 2 / 3 ] [ i − j ] f[0/1/2/3][i-j] f[0/1/2/3][i−j]只用从 k = 1 k=1 k=1转移就行
f[0][i - j] = std::max(f[0][i - j], dp[i - 1][j - 1] - a[i] - b[i]);f[1][i - j] = std::max(f[1][i - j], dp[i - 1][j - 1] + a[i] - b[i]);f[2][i - j] = std::max(f[2][i - j], dp[i - 1][j - 1] - a[i] + b[i]);f[3][i - j] = std::max(f[3][i - j], dp[i - 1][j - 1] + a[i] + b[i]);
- 记住f数组要初始化为负无穷,不能是0
memset(f,0x80,sizeof(f));
- 整体代码
#include <iostream>
#include <cstring>
#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;
const int maxn = 3005;
typedef long long ll;
const ll mod = 998244353;
int a[maxn], b[maxn];
ll dp[maxn][maxn], f[4][maxn];
int main() {//freopen("1.txt","r",stdin);int T;scanf("%d",&T);while(T --) {int n, k;scanf("%d%d",&n,&k);memset(f,0x80,sizeof(f));// 这个0x80初始化出来是复数 for(int i = 1; i <= n; ++ i) cin >> a[i];for(int i = 1; i <= n; ++ i) cin >> b[i]; for(int i = 1; i <= n; ++ i) {for(int j = 1; j <= k && j <= i; ++ j) {dp[i][j] = dp[i-1][j];f[0][i - j] = std::max(f[0][i - j], dp[i - 1][j - 1] - a[i] - b[i]);f[1][i - j] = std::max(f[1][i - j], dp[i - 1][j - 1] + a[i] - b[i]);f[2][i - j] = std::max(f[2][i - j], dp[i - 1][j - 1] - a[i] + b[i]);f[3][i - j] = std::max(f[3][i - j], dp[i - 1][j - 1] + a[i] + b[i]);dp[i][j] = std::max(dp[i][j], f[0][i - j] + a[i] + b[i]);dp[i][j] = std::max(dp[i][j], f[1][i - j] + a[i] - b[i]);dp[i][j] = std::max(dp[i][j], f[2][i - j] - a[i] + b[i]);dp[i][j] = std::max(dp[i][j], f[3][i - j] - a[i] - b[i]);
// for(int h = 1; h <= j; ++ h) {
// dp[i][j] = max(dp[i-h][j-h]+abs(a[i]-b[i-h+1])+abs(a[i-h+1]-b[i]),dp[i][j]);
// // printf("%d %d %lld\n",i,j,dp[i][j]);
// }}}printf("%lld\n",dp[n][k]);} return 0;
}
- 上面你可能会疑问这个不是抵消了吗?
f[0][i - j] = std::max(f[0][i - j], dp[i - 1][j - 1] - a[i] - b[i]);
dp[i][j] = std::max(dp[i][j], f[0][i - j] + a[i] + b[i]);
注意其实这里的有个影响是 f [ 0 ] [ i − j ] f[0][i - j] f[0][i−j]是包含了带 k k k的参数 所以要做两次 m a x max max, d p [ i − 1 ] [ j − 1 ] − a [ i ] − b [ i ] dp[i - 1][j - 1] - a[i] - b[i] dp[i−1][j−1]−a[i]−b[i]只是刚好这一层儿而已
相关文章:
Codeforces Round 892 (Div. 2) - E. Maximum Monogonosity 思维dp 详细解析
题目链接 好久没有写题了复健一下qwq 题目大意 解题思路 这题目还挺妙的 首先考虑比较正常的dp, d p [ i ] [ j ] dp[i][j] dp[i][j] 为前 i i i的长度选 j j j个长度的最大价值,那么转移方程是: 图片来自:图片来源 但是这个是 …...

R语言中的数据重塑
文章目录 介绍reshape2::melt()的用法实例 reshape2::dcast()的用法实例 tidyr::gather()的用法tidyr::spread()的用法 介绍 tidyverse系列包中的函数操作都是针对简洁数据框进行的,对于不是简洁的数据,实现需要进行数据重塑。数据重塑主要包括长宽表的…...

基于Java实现的社区团购系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言系统功能具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域…...

nodejs+vue网上婚纱购物系统elementui
便了用户足不出门也能进行购物的理念,方便了婚纱影楼的对商品的进一步管理,互联网成为人们快速获取、发布、和传递信息的重要渠道,它在人们政治、经济、生活等各个方面发挥着重要的作用。未来的时代是网络信息的时代,“网上生活方式”是人类今…...
【2023集创赛】加速科技杯三等奖作品:私密性高精度刷手身份认证系统
本文为2023年第七届全国大学生集成电路创新创业大赛(“集创赛”)加速科技杯三等奖作品分享,参加极术社区的【有奖征集】分享你的2023集创赛作品,秀出作品风采,分享2023集创赛作品扩大影响力,更有丰富电子礼…...

1500*C. Kefa and Park(dfstree)
Kefa and Park - 洛谷 Problem - 580C - Codeforces Examples input 4 1 1 1 0 0 1 2 1 3 1 4 output 2 input 7 1 1 0 1 1 0 0 0 1 2 1 3 2 4 2 5 3 6 3 7 output 2 解析: dfs遍历,记录前一个结点权值是否为1,并且累计路径1的个数…...

【2023保研】双非上岸东南网安
个人情况 学校:henu 专业:信息安全 排名:1/66 英语:六级500 竞赛:蓝桥杯PB国一,ISCC国一,密码数学挑战赛国三,还有其他一些省级水奖 论文:一篇EI在投(三作通…...

Redis与Mybatis
作者在学习Redis整合时使用JDBC与Jedis,但是呢,现如今的环境下,Mybatis系列ORM框架是更受关注的方法,作者有一点点Mybatis基础,Mybatisplus几乎忘的差不多了,现对Redis整合Mybatis相关知识进行梳理…...

MySQL架构 InnoDB存储引擎
1. 什么是Mysql? 我们在开发的时候,我们都需要对业务数据进行存储,这个时候,你们就会用到MySQL、Oracal等数据库。 MySQL它是一个关系型数据库,这种关系型数据库就有Oracal、 MySQL,以及最近很火的PgSQL等。…...

K8S-CNI
CNI的设计思想即为:Kubernetes在启动Pod的pause容器之后,直接调用CNI网络插件,从而实现为Pod内部应用容器月在的Network Namespace配置符合预期的网络信息。 这里面需要特别关注两个方面:Container必须有自己的网络命名空间的环境,也就是end…...
和命令 (数据类型 四))
Redis 集合类型(Set)和命令 (数据类型 四)
集合类型是一个无序、不重复的数据集合,它可以用于存储唯一的值,并提供了对集合进行交集、并集、差集等操作。 常用集合类型命令: 添加操作: sadd key member1 member2 …:向集合中添加一个或多个成员。 # 添加三个…...
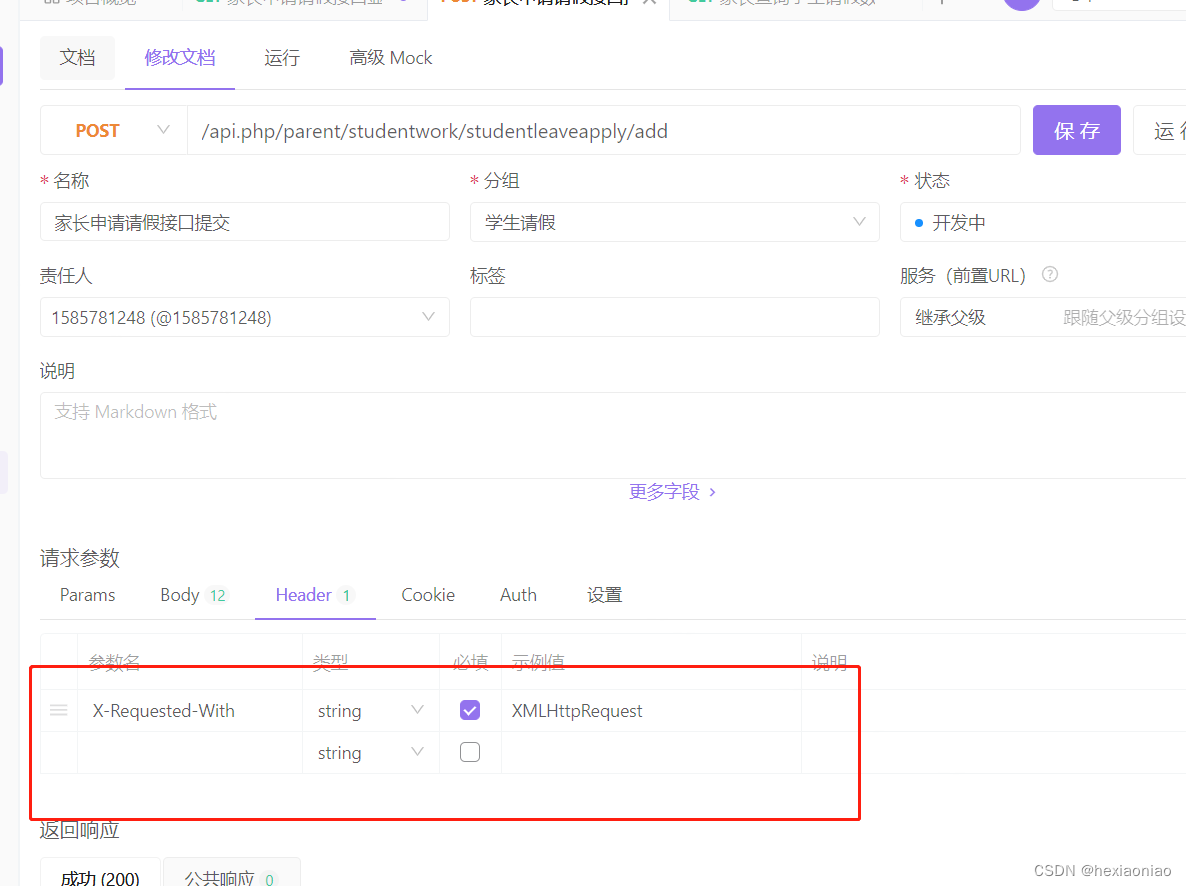
thinkphp5 如何模拟在apifox里面 post数据接收
tp5里面控制器写的方法想直接apifox里面请求接受 必须带上这个参数 header里面 X-Requested-With:XMLHttpRequest...

建造者模式 创建型模式之三
想要搞清楚建造者模式,首先先要了解建造者模式种四个角色的定位 1.Product:表示被构造的复杂对象,就是我们要建造的东西,比如我们要做一个手机,手机就是product。 2.Builder:建造者,这里需要着…...
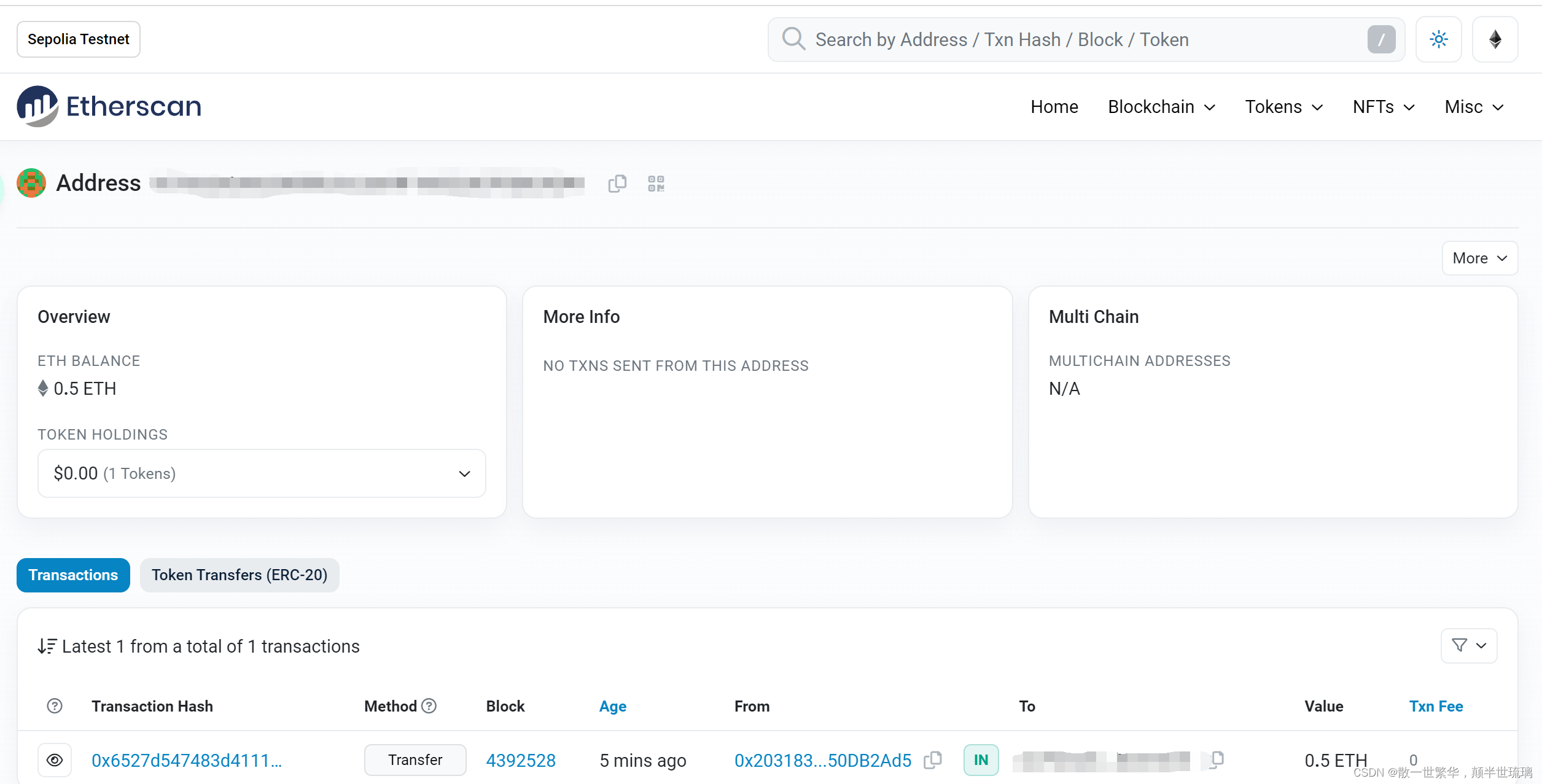
发布以太坊测试网络中的第一笔交易
1.安装以太坊钱包 要想发送发布以太坊测试网络中的第一笔交易,首先需要创建一个管理账户的钱包,这个钱包可以理解为管理私钥的容器,具体按照步骤为:打开Chrome浏览器应用商店搜索MetaMask,选择对应的钱包添加至Chrome…...

No module named ipykernel解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...
Java 基于 SpringBoot 的校园疫情防控系统
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 文章目录 1 简介2.主要技术3 需求分析4系统设计4.1功能结构4.2 数据库设计4.2.1 数据库E/R图4.2.2 数据库表…...

windows的ui自动化测试相关
一个python第三方模块uiautomation github上也有源码,可以看下 uiautomation模块项目地址:https://github.com/yinkaisheng/Python-UIAutomation-for-Windows uiautomation模块项目地址...
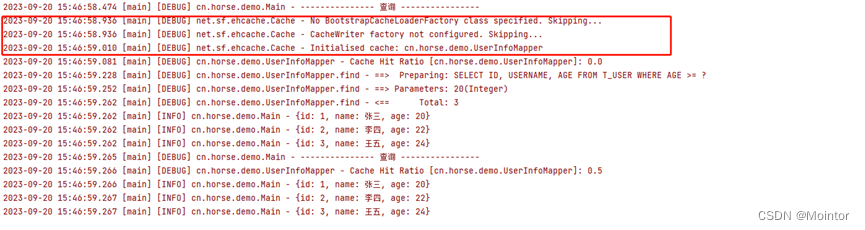
Mybatis 二级缓存(使用Ehcache作为二级缓存)
上一篇我们介绍了mybatis中二级缓存的使用,本篇我们在此基础上介绍Mybatis中如何使用Ehcache作为二级缓存。 如果您对mybatis中二级缓存的使用不太了解,建议您先进行了解后再阅读本篇,可以参考: Mybatis 二级缓存https://blog.c…...
C语言 Cortex-A7核 IIC实验
iic.h #ifndef __IIC_H__ #define __IIC_H__ #include "stm32mp1xx_gpio.h" #include "stm32mp1xx_rcc.h" /* 通过程序模拟实现I2C总线的时序和协议* GPIOF ---> AHB4* I2C1_SCL ---> PF14* I2C1_SDA ---> PF15** */#define SET_SDA_OUT do{…...
【每日一题】2769. 找出最大的可达成数字
2769. 找出最大的可达成数字 - 力扣(LeetCode) 给你两个整数 num 和 t 。 如果整数 x 可以在执行下述操作不超过 t 次的情况下变为与 num 相等,则称其为 可达成数字 : 每次操作将 x 的值增加或减少 1 ,同时可以选择将 …...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
