线性代数(七) 矩阵分析
前言
从性线变换我们得出,矩阵和函数是密不可分的。如何用函数的思维来分析矩阵。
矩阵的序列

通过这个定义我们就定义了矩阵序列的收敛性。

研究矩阵序列收敛性的常用方法,是用《常见向量范数和矩阵范数》来研究矩阵序列的极限。
长度是范数的一个特例。事实上,Frobenius范数对应的就是长度。我们在线性空间中定义内积时,就是把这三条性质作为公理来定义内积的
收敛矩阵
在矩阵序列中,最常见的是由一个方阵的幂构成的序列,关于这样的矩阵序列有如下概念和收敛定理:

r(A)是谱半径是一个矩阵的特征值绝对值中的最大值,用于描述矩阵的特征值的尺度大小。
矩阵级数


矩阵幂级数

- 根据幂级数收敛半径定理求出收敛半径r
- 根据《常见向量范数和矩阵范数》将矩阵A量化,看否在收敛区间中

- 即 a k = k = > r = lim k → ∞ | a k + 1 a k | = | k + 1 k | = 1 a_k= k => r= \lim\limits_{k \to \infty} |\dfrac{a_{k+1}}{a_k}|=|\dfrac{{k+1}}{k}|= 1 ak=k=>r=k→∞lim|akak+1|=|kk+1|=1
- 由范式2得到 p ( A ) = 5 6 p(A)=\dfrac{5}{6} p(A)=65
Neumann级数


- 注1:假设E-A不可逆,那么E-A有0特征值,A的特征值为1。而A的谱半径小于1,矛盾,故E-A可逆
- 注2:A的谱半径小于1,由定理3可知A为收敛矩阵。那么 A k + 1 A^{k+1} Ak+1 就趋近于0(k趋于无穷)
矩阵函数

矩阵函数的计算
常用的有以下几种方法
待定系数法
- 求矩阵A的特征多项式 ∣ λ I − A ∣ |\lambda I - A| ∣λI−A∣
- 利用Hamilton-Cayley定理,求出A的一次性化零多项式 ψ ( A ) = 0 \psi(A)=0 ψ(A)=0
 - 求解 f ( A ) f(A) f(A)多项式
- 求解 f ( A ) f(A) f(A)多项式

- 当 A = λ ,即 ψ ( A ) = f ( A ) A=\lambda, 即\psi(A)=f(A) A=λ,即ψ(A)=f(A)

- sin的导注是cos
- e x e^x ex的导数是它本身的导数,因此, e ( 2 t ) 的导数是 2 e ( 2 t ) e^(2t) 的导数是 2e^(2t) e(2t)的导数是2e(2t)。
利用相似对角化
利用Jordan标准形
主要参考
《常见向量范数和矩阵范数》
《矩阵分析》
《7.2.3幂级数收敛半径定理》
《矩阵序列与矩阵级数》
《矩阵函数的常见求法》
相关文章:

线性代数(七) 矩阵分析
前言 从性线变换我们得出,矩阵和函数是密不可分的。如何用函数的思维来分析矩阵。 矩阵的序列 通过这个定义我们就定义了矩阵序列的收敛性。 研究矩阵序列收敛性的常用方法,是用《常见向量范数和矩阵范数》来研究矩阵序列的极限。 长度是范数的一个特…...
myArm 全新七轴桌面型机械臂
引言 在不断演进的科技世界中,我们始终追求创新和卓越,以满足客户的需求并超越他们的期望。今天,我们很高兴地宣布我们的最新产品——myArm 300 Pi,一款七轴的桌面型机械臂。这款产品的独特之处在于其灵活性和可编程性,…...

tomcat乱码解决
解决乱码 1、修改bin\catalina.bat配置文件 修改tomcat的配置文件,找到tomcat路径下的\bin目录下的catalina.bat文件,修改 set “JAVA_OPTS%JAVA_OPTS% %JSSE_OPTS% -Dfile.encodingUTF-8 -Dsun.jnu.encodingUTF-8 ” 2、修改conf\logging.properties配置…...

【Linux】详解线程第三篇——线程同步和生产消费者模型
线程同步和生消模型 前言正式开始再次用黄牛抢票来讲解线程同步的思想通过条件变量来实现线程同步条件变量接口介绍初始化和销毁pthread_cond_waitsignal和broadcast 生产消费者模型三种关系用基本工程师思维再次理解基于生产消费者模型的阻塞队列版本一版本二多生多消 利用RAI…...

k8s 安装
文章目录 k8s 客户端安装k8s集群minikubekindkubeadm 验证 k8s 客户端 用于连接k8s集群,建议下载1.23.x的版本,其他的版本本地运行可能会有莫名其妙的报错 https://dl.k8s.io/release/v1.23.16/bin/linux/amd64/kubectl 安装k8s集群 minikube Minik…...

红队打靶:THE PLANETS: MERCURY打靶思路详解(vulnhub)
目录 写在开头 第一步:主机发现和端口扫描 第二步:Web渗透 第三步:获取初步立足点并搜集信息 第四步:软连接劫持sudo提权 总结与思考 写在开头 本篇博客在自己的理解之上根据大佬红队笔记的视频进行打靶,详述了…...
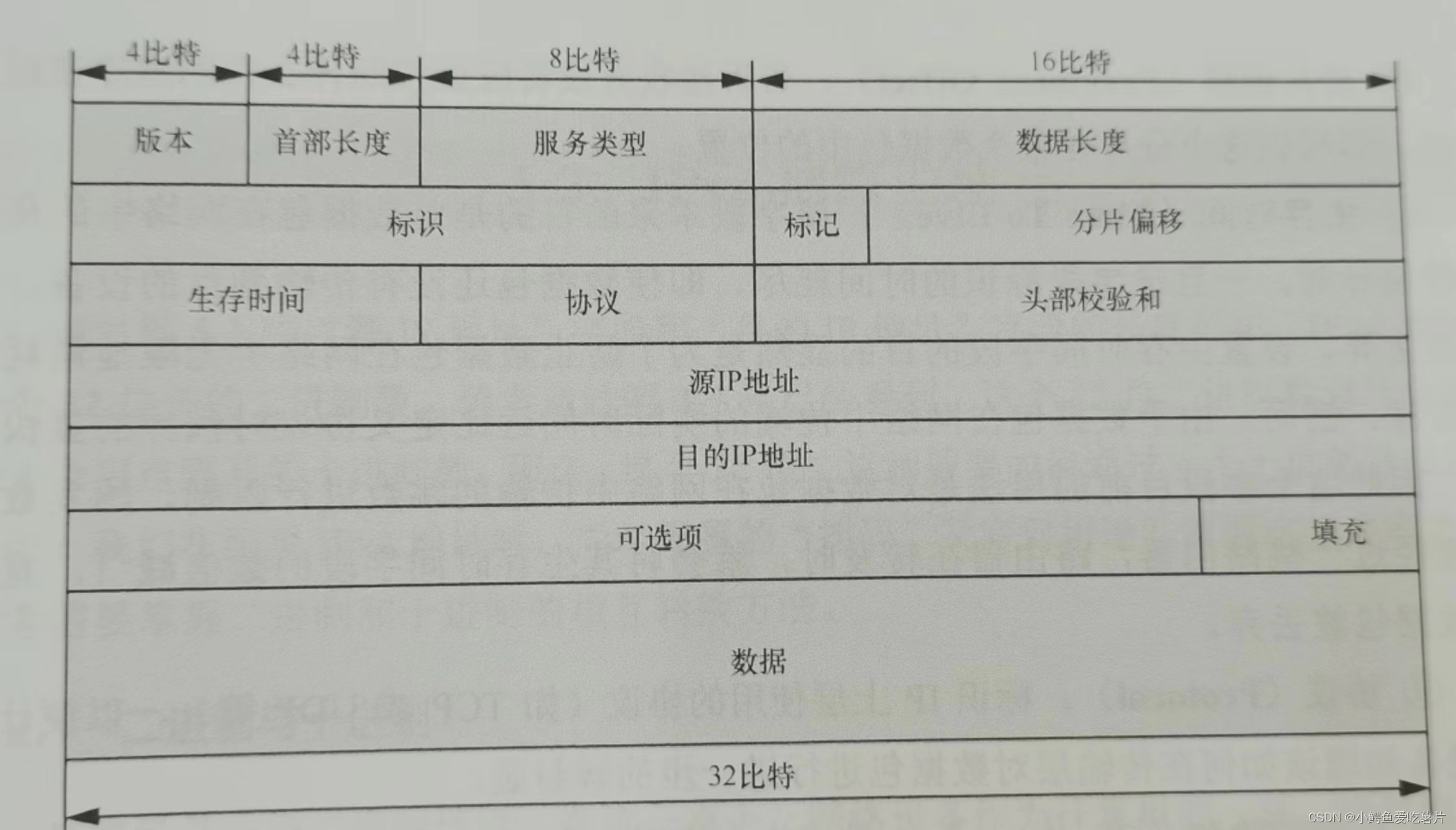
【网络协议】IP
当连接多个异构的局域网形成强烈需求时,用户不满足于仅在一个局域网内进行通信,他们希望通过更高一层协议最终实现异构网络之间的连接。既然需要通过更高一层的协议将多个局域网进行互联,那么这个协议就必须为不同的局域网环境定义统一的寻址…...

Python 布尔类型
布尔值表示两个值之一:True(真)或False(假)。 布尔值 在编程中,您经常需要知道一个表达式是否为True或False。 您可以在Python中评估任何表达式,并获得两个答案之一:True或False。…...

iOS设备管理器iMazing比iTunes好用吗?有哪些优势
虽然 iTunes 是 Apple 官方指定的 iPhone 数据备份和管理工具,但是一直以来 iTunes 卡顿的使用体验和过慢的备份过程为不少人诟病。如果大家也被 iTunes 体验不佳的备份和管理功能所困扰,那么简单易用、功能强大的iMazing 能为你解决这个问题。 iMazing…...

Opengl之深度测试
在坐标系统小节中,我们渲染了一个3D箱子,并且运用了深度缓冲(Depth Buffer)来防止被阻挡的面渲染到其它面的前面。在这一节中,我们将会更加深入地讨论这些储存在深度缓冲(或z缓冲(z-buffer))中的深度值(Depth Value),以及它们是如何确定一个片段是处于其它片段后方的。 …...

利用ICG-NH2/Amine进行DNA标记1686147-55-6星戈瑞
ICG-NH2(吲哚菁绿胺)可以用于DNA标记,这种标记方法通常涉及到DNA上的胺基反应基团和ICG-NH2之间的化学反应。以下是一种常见的方法,用于利用ICG-NH2标记DNA分子: 步骤: 1.准备目标DNA:你需要准…...

Pyecharts数据可视化
Pyecharts数据可视化 1、Pyecharts模块2、柱状图3、折线图4、饼图5、散点图6、图表合并7、词云8、地图 1、Pyecharts模块 ECharts是百度提供的基于JavaScript的开源可视化库,主要用于Web端数据可视化 Echarts是通过JS实现的,Pyecharts则可以使用Python来…...
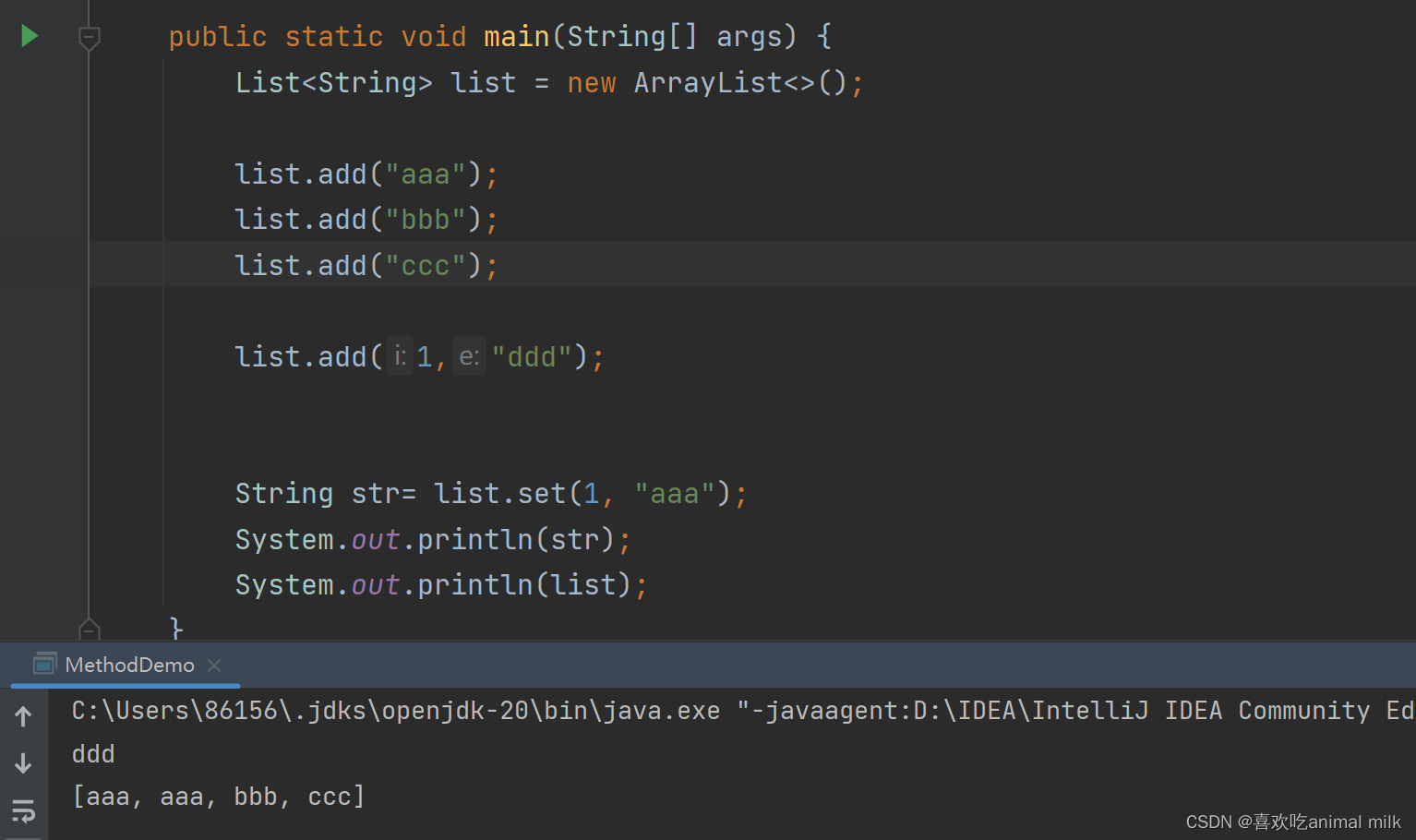
集合-List集合
系列文章目录 1.集合-Collection-CSDN博客 2.集合-List集合-CSDN博客 文章目录 目录 系列文章目录 文章目录 前言 一 . 什么是List? 二 . List集合的特点 三 . 常用方法 1.void add(int index, E element): 将指定的元素插入到列表的指定位置。 2.E remove(int in…...

vuex的使用
1 vuex的使用 1 vuex的使用 store/index.js -在Vue中实现集中式状态(数据)管理的一个Vue插件,对vue应用中多个组件的共享状态进行集中式 的管理(读/写),也是一种组件间通信的方式,且适用于任意…...
raw图片处理软件:DxO PhotoLab 6 mac中文版支持相机格式
DxO PhotoLab 6 mac是一款专业的RAW图片处理软件,适用于Mac操作系统。它具有先进的图像处理技术和直观易用的界面,可帮助用户轻松地将RAW格式的照片转换为高质量的JPEG或TIFF图像。 DxO PhotoLab 6支持多种相机品牌的RAW格式,包括佳能、尼康、…...

ReactPortals传送门
ReactPortals传送门 React Portals提供了一种将子节点渲染到父组件以外的DOM节点的解决方案,即允许将JSX作为children渲染至DOM的不同部分,最常见用例是子组件需要从视觉上脱离父容器,例如对话框、浮动工具栏、提示信息等。 描述 <div&…...
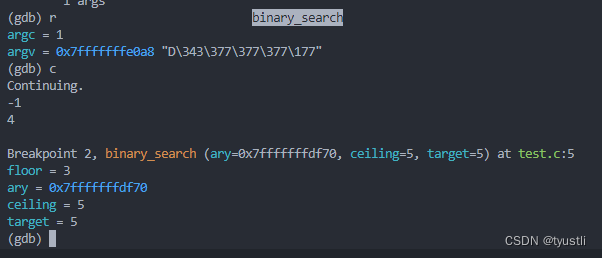
【GDB】 command 命令
GDB command 命令 语法 command 命令是一个很好用的调试命令,它配合断点使用,可以在指定的断点执行预先设置的命令 其语法为:command bread_id,这样会提示你输入你要执行的命令,以 end 结束。这个 bread_id 就是用 …...

1038 统计同成绩学生
输入样例: 10 60 75 90 55 75 99 82 90 75 50 3 75 90 88 输出样例: 3 2 0 solution #include <stdio.h> int main(){int n, d, k, hash[101] {0}, a[100000];scanf("%d", &n);for(int i 0; i < n; i){scanf("%d&quo…...

git报错:Failed to connect to 127.0.0.1 port 1080
Bug描述 由于在试了网上的这条命令 git config --global http.proxy socks5 127.0.0.1:1080 git config --global https.proxy socks5 127.0.0.1:1080git config --global http.proxy 127.0.0.1:1080 git config --global https.proxy 127.0.0.1:1080Bug描述:Faile…...
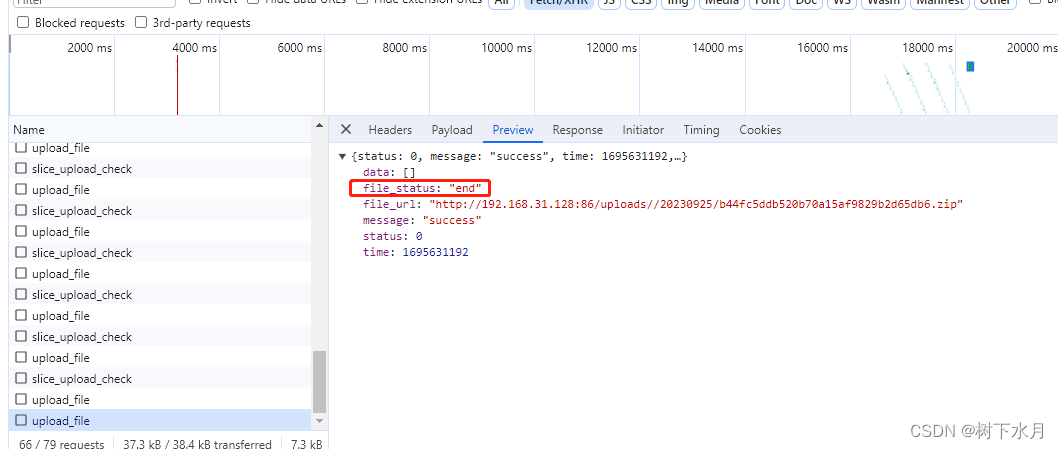
php eayswoole node axios crypto-js 实现大文件分片上传复盘
不啰嗦 直接上步骤 步骤1.开发环境配置 项目需要node.js 做前端支撑 官网下载地址: http://nodejs.cn/download/ 根据自己需要下载对应的版本,我下载的是windows系统64位的版本。 包下载好后 进行安装,安装步骤在此省略... 测试是否安装成功 …...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...


