【python】python实现杨辉三角的三种方法
文章目录
- 1.杨辉三角介绍:
- 2.方法一:迭代
- 3.方法二:生成器
- 4.方法三:递归
1.杨辉三角介绍:
杨辉三角是一种数学图形,由数字排列成类似三角形的形状。它的每个数值等于它上方两个数值之和。这个三角形的形状可以用一个二维表格来表示,其中每个位置上的数值都是通过前一行的数值计算得到的。在这个三角形中,第一行只有一个数值1,第二行有两个数值1,第三行有三个数值1,以此类推。从第四行开始,除了首尾的1之外,中间的数值是上一行对应位置的两个数值之和。 下面是一些杨辉三角常见的特点和应用:
- 对称性:杨辉三角以中心轴为对称轴,每行的对称位置上的数值相等。
- 组合数性质:杨辉三角中的数值可以表示为组合数,例如,第n行第k个数值表示为C(n-1, k-1),即从n-1个物体中选取k-1个的组合数。
- 幂和性质:杨辉三角的每一行的数值之和都是2的幂,例如,第n行的数值之和为2^(n-1)。
- 整数序列性质:杨辉三角的每一行对应着一个整数序列,如斐波那契数列、自然数序列等。
杨辉三角不仅仅是一个有趣的数学图形,还有许多实际应用。它在组合数学、概率论、代数等领域都有重要的应用,例如计算二项式的展开系数、解决概率分布问题、生成多项式系数等。
通过编程语言(如Python),可以实现杨辉三角并以可视化的方式显示出来。这样的程序可以逐行计算并输出杨辉三角的数值,从而更好地展示其规律和特点,并可用于相关计算和问题求解。
2.方法一:迭代
代码试例:
def triangle_1(x):""":param x: 需要生成的杨辉三角行数:return:"""triangle = [[1], [1, 1]] # 初始化杨辉三角n = 3 # 从第三行开始计数,逐行添加while n <= x:for i in range(0, n-1):if i == 0:# 添加初始列表[1,1],杨辉三角每行的首位和末位必为1triangle.append([1, 1])else:# 逐位计算,并插入初始列表中triangle[n-1].insert(i, triangle[n - 2][i] + triangle[n - 2][i - 1])n += 1return triangle
x = 11
triangle = triangle_1(x)# 遍历结果,逐行打印
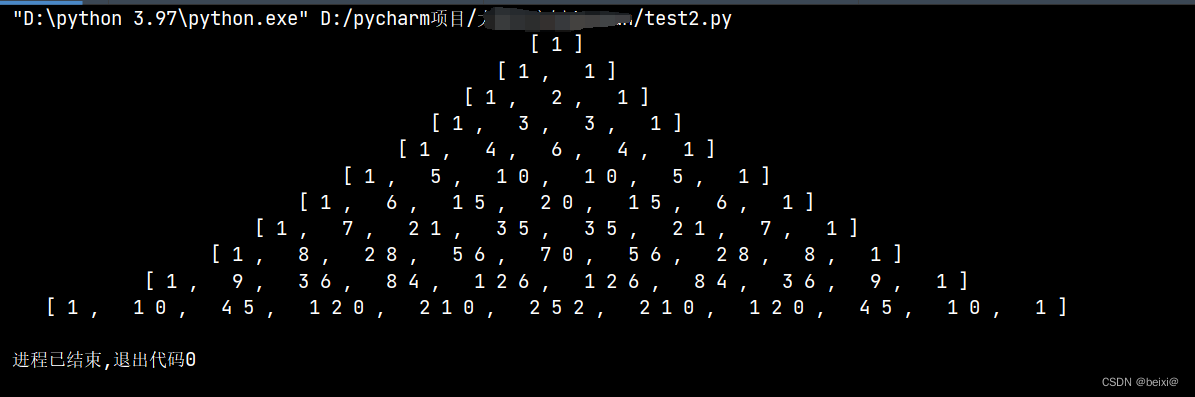
for i in range(x):print(' '.join(str(triangle[i])).center(100)) # 转为str,居中显示
运行结果:
3.方法二:生成器
代码试例:
def triangle_2(n):""":param n: 需要生成的杨辉三角行数:return: """triangle = [1] # 初始化杨辉三角for i in range(n):yield triangletriangle.append(0) # 在最后一位加个0,用于计算下一行triangle = [triangle[i] + triangle[i - 1] for i in range(len(triangle))]
# 从生成器取值
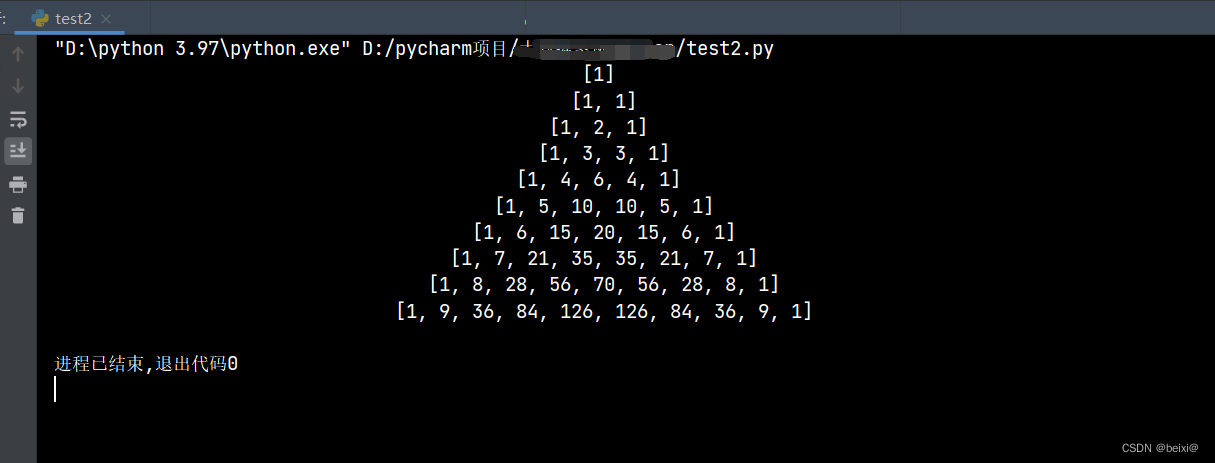
for i in triangle_2(10):print(''.join(str(i)).center(100)) # 格式化输出
运行结果:
4.方法三:递归
杨辉三角特性:
【1,1】=【0,1】+【1,0】
【1,2,1】=【0,1,1】+【1,1,0】
【1,3,3,1】=【0,1,2,1】+【1,2,1,0】
【1,4,6,4,1】=【0,1,3,3,1】+【1,3,3,1,0】
第n行等于第n-1行分别首尾补0,然后按位相加
试例代码:
def triangle_3(n):""":param n:需要生成的杨辉三角行数:return:"""triangle = [1] # 初始化杨辉三角if n == 0:return trianglereturn [x+y for x, y in zip([0] + triangle_4(n - 1), triangle_4(n - 1) + [0])]
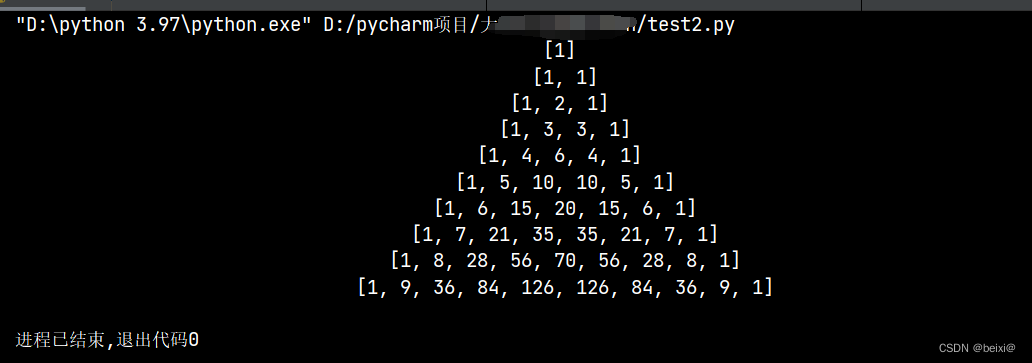
for i in range(10):print(''.join(str(triangle_4(i))).center(100))
运行结果:
到此这篇关于python实现杨辉三角的三种方法代码实例的文章就介绍到这了,如果本篇文章对你有帮助,记得点赞收藏+关注哦~
相关文章:

【python】python实现杨辉三角的三种方法
文章目录 1.杨辉三角介绍:2.方法一:迭代3.方法二:生成器4.方法三:递归 1.杨辉三角介绍: 杨辉三角是一种数学图形,由数字排列成类似三角形的形状。它的每个数值等于它上方两个数值之和。这个三角形的形状可以…...

GitHub 基本操作
最近要发展一下自己的 github 账号了,把以前的项目代码规整规整上传上去,这里总结了一些经验,经过数次实践之后,已解决几乎所有基本操作中的bug,根据下面的操作步骤来,绝对没错了。(若有其他问题…...

Docker和Docker compose的安装使用指南
一,环境准备 Docker运行需要依赖jdk,所以需要先安装一下jdk yum install -y java-1.8.0-openjdk.x86_64 二,Docker安装和验证 1,安装依赖工具 yum install -y yum-utils 2,设置远程仓库 yum-config-manager --add-r…...

51单片机控制电动机正反转,PWM调速,记录转动圈数。
今天的实验需要用到的材料有:51单片机最小系统,4X4的矩阵键盘,DC直流6V-12V带编码器电机,L298N模块,一个led小灯。下面把产品截图展示一下: 单片机就不展示了,都一样,下面是接线图&a…...
)
JAVA学习(方法的定义和调用)
一、方法的定义和调用 1、关键词:static表示静态方法,如没有返回值使用void,方法名前使用类型,例如int、float等; /*** 测试方法的定义和调用*/public class TestMethod {public static void main(String[] args) {a…...

Linux(CentOS/Ubuntu)——安装nginx
如果确定你的系统是基于CentOS或RHEL,可以使用以下命令: ①、安装库文件 #安装gcc yum install gcc-c#安装PCRE pcre-devel yum install -y pcre pcre-devel#安装zlib yum install -y zlib zlib-devel#安装Open SSL yum install -y openssl openssl-de…...

26962-2011 高频电磁场综合水处理器技术条件
声明 本文是学习GB-T 26962-2011 高频电磁场综合水处理器技术条件. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们 1 范围 本标准规定了高频电磁场综合水处理器(以下简称处理器)的术语和定义、分类和型号、结构型式、 要求及检验、标志、包装和贮运…...

图扑软件受邀亮相 IOTE 2023 国际物联网展
IOTE 2023 国际物联网展,作为全球物联网领域的盛会,于 9 月 20 日 - 22 日在中国深圳拉开帷幕。本届展会以“IoT构建数字经济底座”为主题,由深圳市物联网产业协会主办,打造当前物联网最新科技大秀。促进物联网与各行业深度融合&a…...
C语言文件操作与管理
一、为什么使用文件 在我们前面练习使用结构体时,写通讯录的程序,当通讯录运行起来的时候,可以给通讯录中增加、删除数据,此时数据是存放在内存中,当程序退出的时候,通讯录中的数据自然就不存在了ÿ…...
蓝桥等考Python组别八级005
第一部分:选择题 1、Python L8 (15分) 运行下面程序,输出的结果是( )。 i 1 while i < 4: print(i, end ) i 1 1 2 30 1 2 31 2 3 40 1 2 3 4 正确答案:C 2、Python L8 &#…...

JUnit介绍
JUnit是用于编写和运行可重复的自动化测试的开源测试框架, 这样可以保证我们的代码按预期工作。JUnit可广泛用于工业和作为支架(从命令行)或IDE(如Eclipse)内单独的Java程序。 JUnit提供: 断言测试预期结果。 测试功能共享通用的测试数据。 测试套件轻…...
(高阶) Redis 7 第16讲 预热/雪崩/击穿/穿透 缓存篇
面试题 什么是缓存预热/雪崩/击穿/穿透如何做缓存预热如何避免或减少缓存雪崩穿透和击穿的区别?穿透和击穿的解决方案出现缓存不一致时,有哪些修补方案缓存预热 理论 将需要的数据提前加载到缓存中,不需要用户使用的过程中进行数据回写。(比如秒杀活动数据等) 方案 1.…...

(三) gitblit管理员手册
(一)gitblit安装教程 (二) gitblit用户使用教程 (三) gitblit管理员手册 目录 权限管理创建仓库时创建用户普通用户 管理员用户访问限制和访问权限仓库创建权限分配 Teams普通组管理员组 参考资料 权限管理 创建仓库时 选择指定的人员查看,克隆,推送 不允许fork 对应Anonymo…...

ESKF算法融合GNSS与IMU信息,航向角的偏差是如何逐渐影响到重力加速度g以及位置偏差的 CSDN gpt
1##############################ESKF算法融合GNSS与IMU信息,航向角的偏差是如何逐渐影响到重力加速度g以及位置偏差的 CSDN gpt 航向角的偏差会逐渐影响重力加速度和位置偏差。首先,航向角的偏差会影响重力加速度的测量值。在ESKF算法中,通过将IMU测…...
Java初始化大量数据到Neo4j中(二)
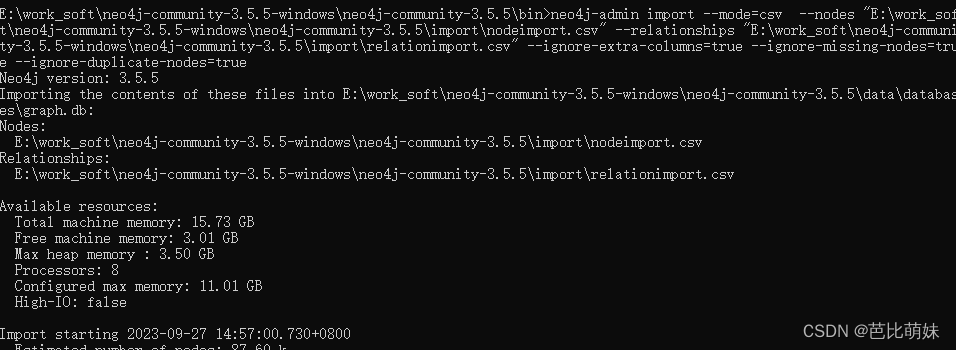
接Java初始化大量数据到Neo4j中(一)继续探索,之前用create命令导入大量数据发现太过耗时,查阅资料说大量数据初始化到Neo4j需要使用neo4j-admin import 业务数据说明可以参加Java初始化大量数据到Neo4j中(一),这里主要是将处理好的节点数据和…...

flink1.17安装
Flink1.17安装 官网地址: https://nightlies.apache.org/flink/flink-docs-release-1.17/zh//docs/try-flink/local_installation/ 安装jdk11 ps:只能安装openjdk11,昨天安装的oracle jdk17,结果怎么也运行不起来。 sudo apt …...

SLAM从入门到精通(gmapping建图)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 前面我们介绍了hector slam建图。相对而言,hector slam建图对数据的要求比较低,只需要lidar数据就可以建图了。但是hector …...
中国312个历史文化名镇及景区空间点位数据集
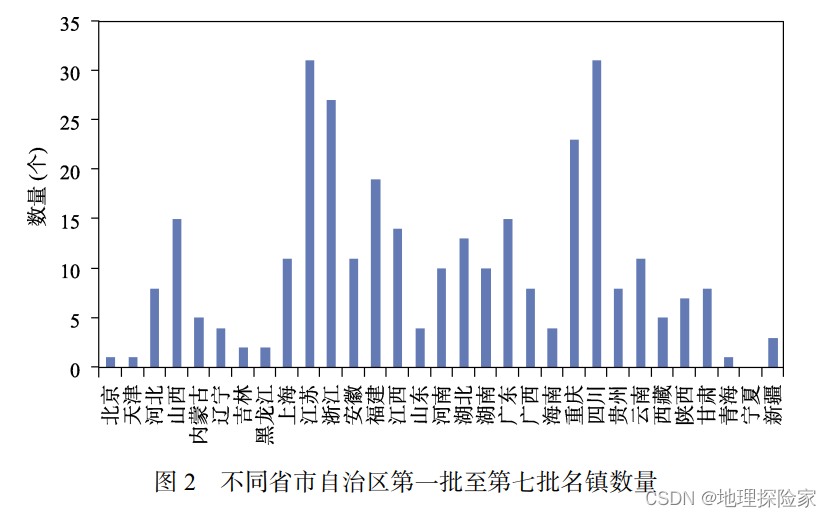
一部中华史,既是人类创造丰富物质财富的奋头史,又是与自然共生共存的和谐史不仅留存下悠久丰富的人文思想和情怀,还在各处镌刻下可流传的生活场景,历史文化名镇(以下简称:名镇)就是这样真实的历史画卷。“镇”是一方的政治文化中心…...

记一次Mybatis驼峰命名导致的线上BUG及处理方案
前言 方向从一开始就错了,还是执着的去寻找问题的解决方案,简直就是一场重大灾难,但这也是每个修行者的必由之路。这个线上问题,差点让我的心里防线崩溃,苦寻无门,最终得以解决也多亏了身边的各路大佬的群…...
在MyBatisPlus中添加分页插件
开发过程中,数据量大的时候,查询效率会有所下降,这时,我们往往会使用分页。 具体操作入下: 1、添加分页插件: package com.zhang.config;import com.baomidou.mybatisplus.extension.plugins.Pagination…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

