【考研数学】概率论与数理统计 —— 第三章 | 二维随机变量及其分布(2,常见的二维随机变量及二维变量的条件分布和独立性)
文章目录
- 引言
- 四、常见的二维随机变量
- 4.1 二维均匀分布
- 4.2 二维正态分布
- 五、二维随机变量的条件分布
- 5.1 二维离散型随机变量的条件分布律
- 5.2 二维连续型随机变量的条件分布
- 六、随机变量的独立性
- 6.1 基本概念
- 6.2 随机变量独立的等价条件
- 写在最后
引言
有了上文关于二维随机变量的基本概念与性质后,我们可以往后继续学习更加深入的内容。
四、常见的二维随机变量
4.1 二维均匀分布
设 ( X , Y ) (X,Y) (X,Y) 为二维随机变量, D D D 为 x O y xOy xOy 平面的有限区域,其面积为 A A A ,若 ( X , Y ) (X,Y) (X,Y) 的联合密度函数为 f ( x , y ) = { 1 A , ( x , y ) ∈ D 0 , ( x , y ) ∉ D , f(x,y)=\begin{cases} \frac{1}{A} ,&(x,y)\in D \\ 0,&(x,y) \notin D \end{cases}, f(x,y)={A1,0,(x,y)∈D(x,y)∈/D, 称 ( X , Y ) (X,Y) (X,Y) 为区域 D D D 上的服从均匀分布。
可以回想一下一维的均匀分布,它是长度的倒数。
4.2 二维正态分布
这个我就不手敲了,太长啦,根本记不住。

其中, ρ \rho ρ 为两个随机变量的相关系数。
若 ( X , Y ) ∼ N ( μ 1 , μ 2 ; σ 1 2 , σ 2 2 ; ρ ) (X,Y)\sim N(\mu_1,\mu_2;\sigma_1^2,\sigma_2^2;\rho) (X,Y)∼N(μ1,μ2;σ12,σ22;ρ) ,则 X ∼ N ( μ 1 , σ 1 2 ) , Y ∼ N ( μ 2 , σ 2 2 ) . X \sim N(\mu_1,\sigma_1^2),Y \sim N(\mu_2,\sigma_2^2). X∼N(μ1,σ12),Y∼N(μ2,σ22). 当 a 2 + b 2 ≠ 0 a^2+b^2 \ne 0 a2+b2=0 时,有 a X + b Y aX+bY aX+bY 服从一维正态分布。随机变量 X X X 和 Y Y Y 独立的充要条件是两个变量不相关,即 ρ ≠ 0 \rho \ne 0 ρ=0 。
五、二维随机变量的条件分布
5.1 二维离散型随机变量的条件分布律
设 ( X , Y ) (X,Y) (X,Y) 为二维离散型随机变量,其联合分布律为 P { X = x i , Y = y j } = p i j ( i = 1 , 2 , ⋯ , m ; j = 1 , 2 , ⋯ , n ) . P\{X=x_i,Y=y_j\}=p_{ij}(i=1,2,\cdots,m;j=1,2,\cdots,n). P{X=xi,Y=yj}=pij(i=1,2,⋯,m;j=1,2,⋯,n). (1)对某个固定的 i i i ,若 P { X = x i } > 0 P\{X=x_i\}>0 P{X=xi}>0 ,则称 P { Y = y j ∣ X = x i } = P { X = x i , Y = y j } P { X = x i } = p i j p i ⋅ ( j = 1 , 2 , ⋯ , n ) P\{Y=y_j | X=x_i\}=\frac{P\{X=x_i,Y=y_j\}}{P\{X=x_i\}}=\frac{p_{ij}}{p_{i\cdot}}(j=1,2,\cdots,n) P{Y=yj∣X=xi}=P{X=xi}P{X=xi,Y=yj}=pi⋅pij(j=1,2,⋯,n) 为在 X = x i X=x_i X=xi 条件下随机变量 Y Y Y 的条件分布律。
(2)对某个固定的 j j j ,若 P { Y = y j } > 0 P\{Y=y_j\}>0 P{Y=yj}>0 ,则称 P { X = x i ∣ Y = y j } = P { X = x i , Y = y j } P { Y = y j } = p i j p ⋅ j ( i = 1 , 2 , ⋯ , m ) P\{X=x_i | Y=y_j\}=\frac{P\{X=x_i,Y=y_j\}}{P\{Y=y_j\}}=\frac{p_{ij}}{p_{\cdot j}}(i=1,2,\cdots,m) P{X=xi∣Y=yj}=P{Y=yj}P{X=xi,Y=yj}=p⋅jpij(i=1,2,⋯,m) 为在 Y = y i Y=y_i Y=yi 条件下随机变量 X X X 的条件分布律。
5.2 二维连续型随机变量的条件分布
设 ( X , Y ) (X,Y) (X,Y) 为二维连续型随机变量,联合密度函数为 f ( x , y ) f(x,y) f(x,y) ,变量 X , Y X,Y X,Y 的边缘密度函数分别为 f X ( x ) , f Y ( y ) . f_X(x),f_Y(y). fX(x),fY(y).
对固定的 X = x X=x X=x ,若 f X ( x ) > 0 f_X(x)>0 fX(x)>0 ,称 P { Y ≤ y ∣ X = x } = ∫ − ∞ y f ( x , y ) f X ( x ) d y P\{Y\leq y | X=x\}=\int_{-\infty}^y\frac{f(x,y)}{f_X(x)}dy P{Y≤y∣X=x}=∫−∞yfX(x)f(x,y)dy 为在 X = x X=x X=x 条件下 Y Y Y 的条件分布函数, f ( x , y ) f X ( x ) \frac{f(x,y)}{f_X(x)} fX(x)f(x,y) 为条件密度函数。对于固定的 Y = y Y=y Y=y ,可同理得到类似结论。
我看老汤也没给证明,自己也没想明白为什么,就上网搜了下,发现是做了近似处理。

六、随机变量的独立性
6.1 基本概念
设 A , B A,B A,B 为两个随机事件,若 P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B) ,称事件 A , B A,B A,B 独立;设 ( X , Y ) (X,Y) (X,Y) 为二维随机变量,令 { X ≤ x } = A , { Y ≤ y } = B \{X\leq x\}=A,\{Y\leq y\}=B {X≤x}=A,{Y≤y}=B ,则 P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B) 等价于 F ( x , y ) = P { X ≤ x , Y ≤ y } = P { X ≤ x } P { Y ≤ y } = F X ( x ) F Y ( y ) . F(x,y)=P\{X\leq x,Y\leq y\}=P\{X\leq x\}P\{Y\leq y\}=F_X(x)F_Y(y). F(x,y)=P{X≤x,Y≤y}=P{X≤x}P{Y≤y}=FX(x)FY(y). 于是有如下定义:
设 ( X , Y ) (X,Y) (X,Y) 为二维随机变量, F ( x , y ) F(x,y) F(x,y) 为其联合分布函数, F X ( x ) , F Y ( y ) F_X(x),F_Y(y) FX(x),FY(y) 分别为 X , Y X,Y X,Y 的边缘分布函数,若 F ( x , y ) = F X ( x ) = F Y ( y ) F(x,y)=F_X(x)=F_Y(y) F(x,y)=FX(x)=FY(y) ,称变量 X , Y X,Y X,Y 相互独立。同理可扩展到 n n n 维。
6.2 随机变量独立的等价条件

设 ( X 1 , X 2 . ⋯ , X m ) (X_1,X_2.\cdots,X_m) (X1,X2.⋯,Xm) 与 ( Y 1 , Y 2 , ⋯ , Y n ) (Y_1,Y_2,\cdots,Y_n) (Y1,Y2,⋯,Yn) 相互独立,则由 ( X 1 , X 2 . ⋯ , X m ) (X_1,X_2.\cdots,X_m) (X1,X2.⋯,Xm) 构成的函数 φ ( X 1 , X 2 . ⋯ , X m ) \varphi(X_1,X_2.\cdots,X_m) φ(X1,X2.⋯,Xm) 与 ( Y 1 , Y 2 , ⋯ , Y n ) (Y_1,Y_2,\cdots,Y_n) (Y1,Y2,⋯,Yn) 构成的函数 φ ( Y 1 , Y 2 , ⋯ , Y n ) \varphi(Y_1,Y_2,\cdots,Y_n) φ(Y1,Y2,⋯,Yn) 相互独立。
写在最后
其实如果一维的能掌握好一些,二维的可以类比来学,下一篇来说说二维随机变量的最后一个内容 —— 二维随机变量函数的分布。
相关文章:

【考研数学】概率论与数理统计 —— 第三章 | 二维随机变量及其分布(2,常见的二维随机变量及二维变量的条件分布和独立性)
文章目录 引言四、常见的二维随机变量4.1 二维均匀分布4.2 二维正态分布 五、二维随机变量的条件分布5.1 二维离散型随机变量的条件分布律5.2 二维连续型随机变量的条件分布 六、随机变量的独立性6.1 基本概念6.2 随机变量独立的等价条件 写在最后 引言 有了上文关于二维随机变…...
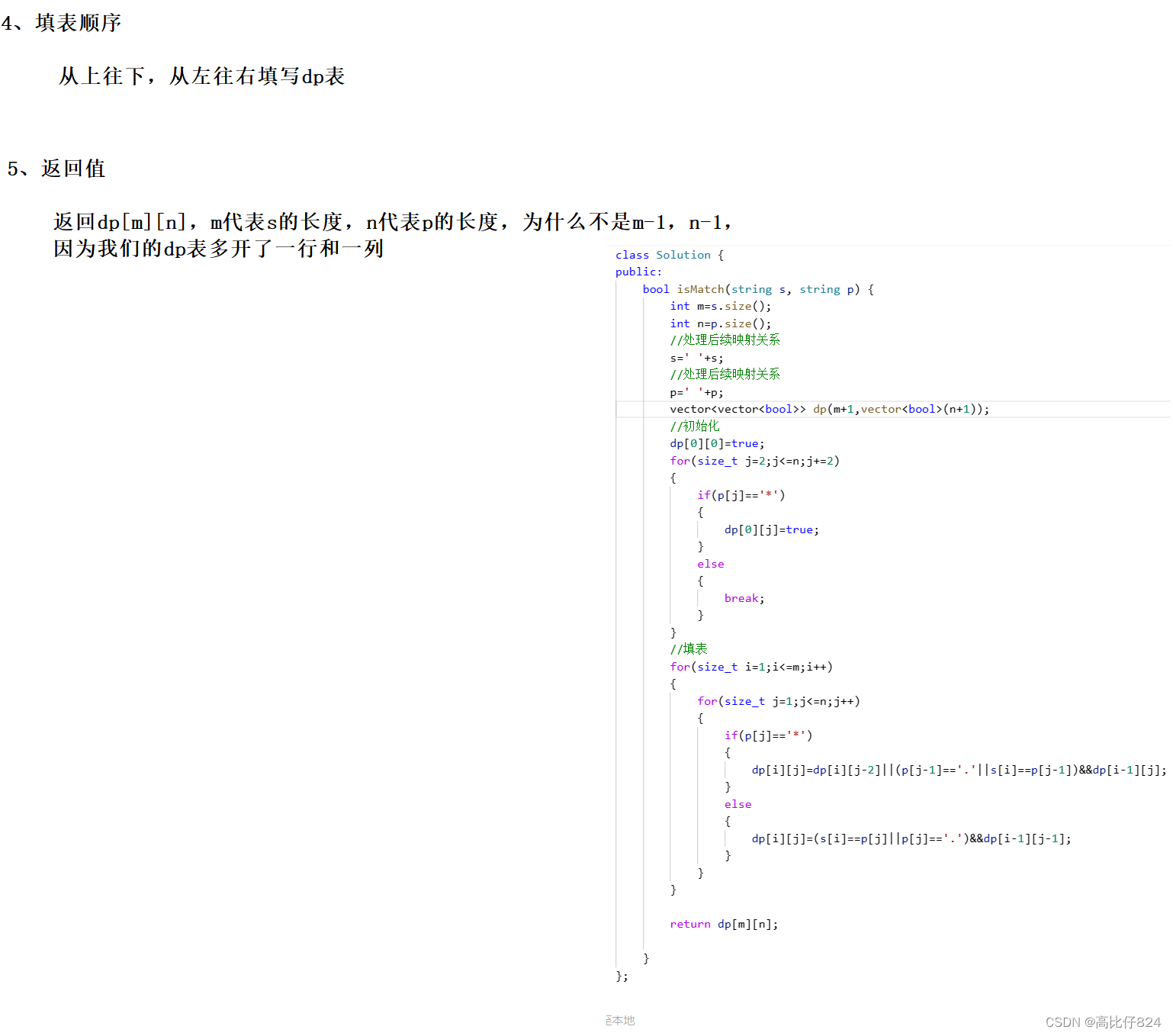
力扣 -- 10. 正则表达式匹配
解题步骤: 参考代码: class Solution { public:bool isMatch(string s, string p) {int ms.size();int np.size();//处理后续映射关系s s;//处理后续映射关系p p;vector<vector<bool>> dp(m1,vector<bool>(n1));//初始化dp[0][0]true…...
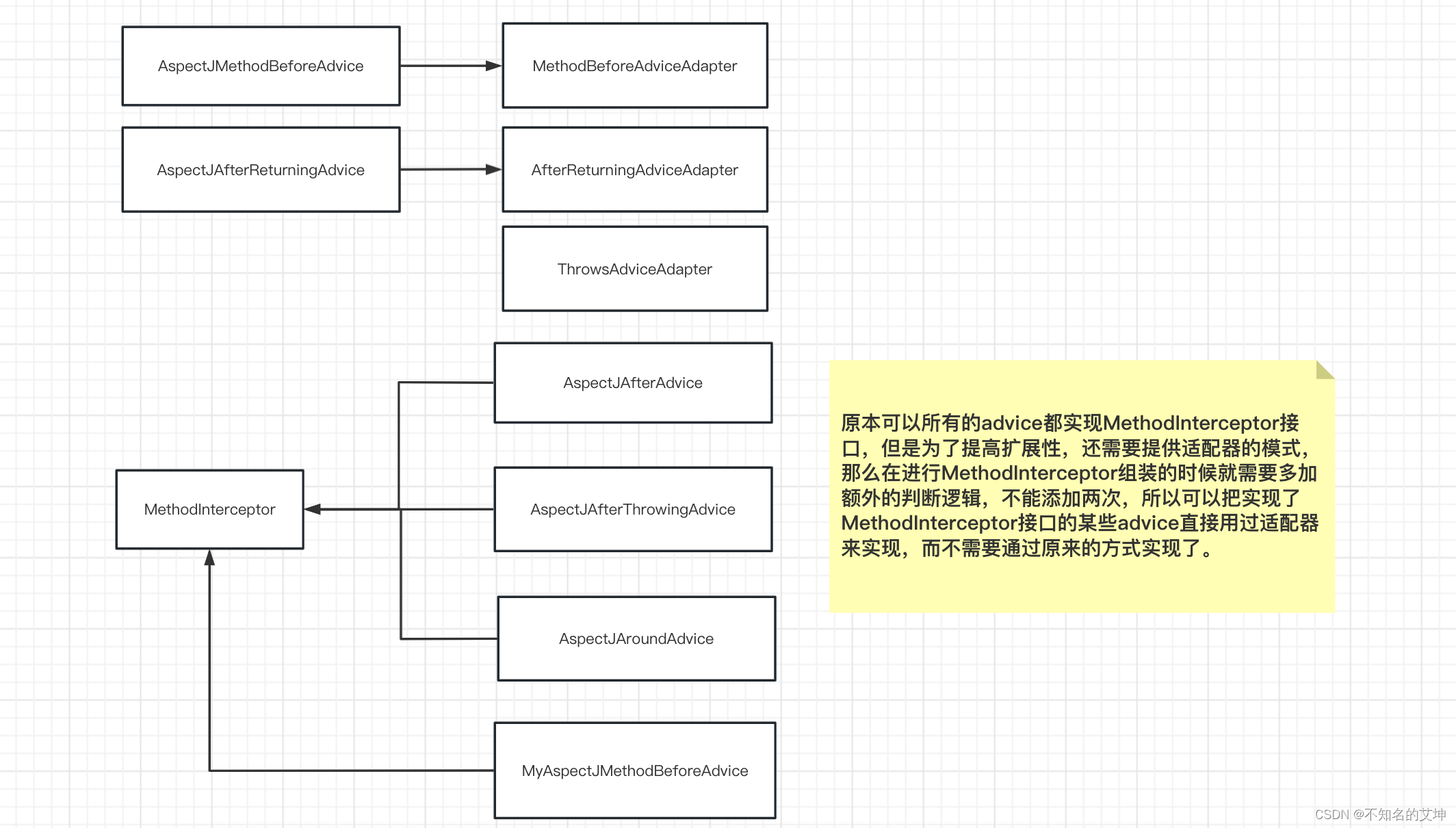
Spring源码分析(四) Aop全流程
一、Spring AOP基础概念 1、基础概念 连接点(Join point):能够被拦截的地方,Spring AOP 是基于动态代理的,所以是方法拦截的,每个成员方法都可以称之为连接点;切点(Poincut):每个方法都可以称之为连接点&…...

定义现代化实时数据仓库,SelectDB 全新产品形态全面发布
导读:9 月 25 日,2023 飞轮科技产品发布会在线上正式召开,本次产品发布会以 “新内核、新图景” 为主题,飞轮科技 CEO 马如悦全面解析了现代化数据仓库的演进趋势,宣布立足于多云之上的 SelectDB Cloud 云服务全面开放…...

Linux系统编程(七):线程同步
参考引用 UNIX 环境高级编程 (第3版)黑马程序员-Linux 系统编程 1. 同步概念 所谓同步,即同时起步、协调一致。不同的对象,对 “同步” 的理解方式略有不同 设备同步,是指在两个设备之间规定一个共同的时间参考数据库同步,是指让…...
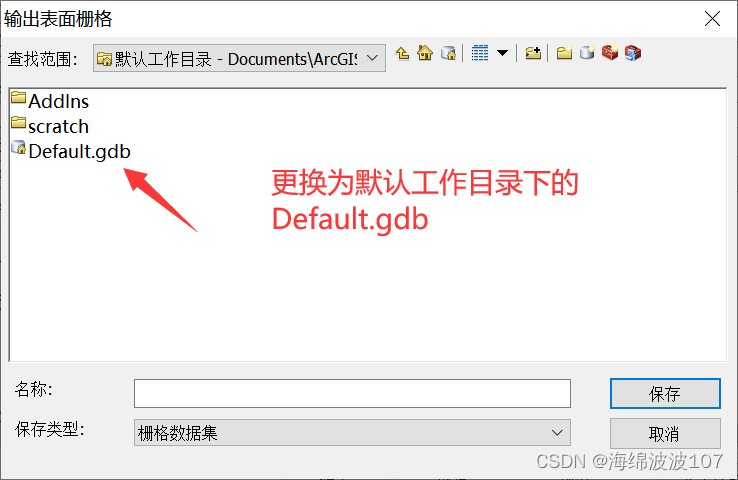
Arcgis克里金插值报错:ERROR 999999: 执行函数时出错。 表名无效。 空间参考不存在。 ERROR 010429: GRID IO 中存在错误
ERROR 999999: 执行函数时出错。 问题描述 表名无效。 空间参考不存在。 ERROR 010429: GRID IO 中存在错误: WindowSetLyr: Window cell size does not match layer cell size. name: c:\users\lenovo\appdata\local\temp\arc2f89\t_t164, adepth: 32, type: 1, iomode: 6, …...

【网络协议】ARP协议
为什么网络需要同时借助MAC地址这种物理地址和IP地址这种逻辑地址进行通信? 尽管目前MAC地址可以通过逻辑的方式进行修改,但它最初是被设计为不可人为更改的硬件地址。虽然MAC地址也可以满足唯一性的要求,但由于它不可由管理员根据需求通过逻…...
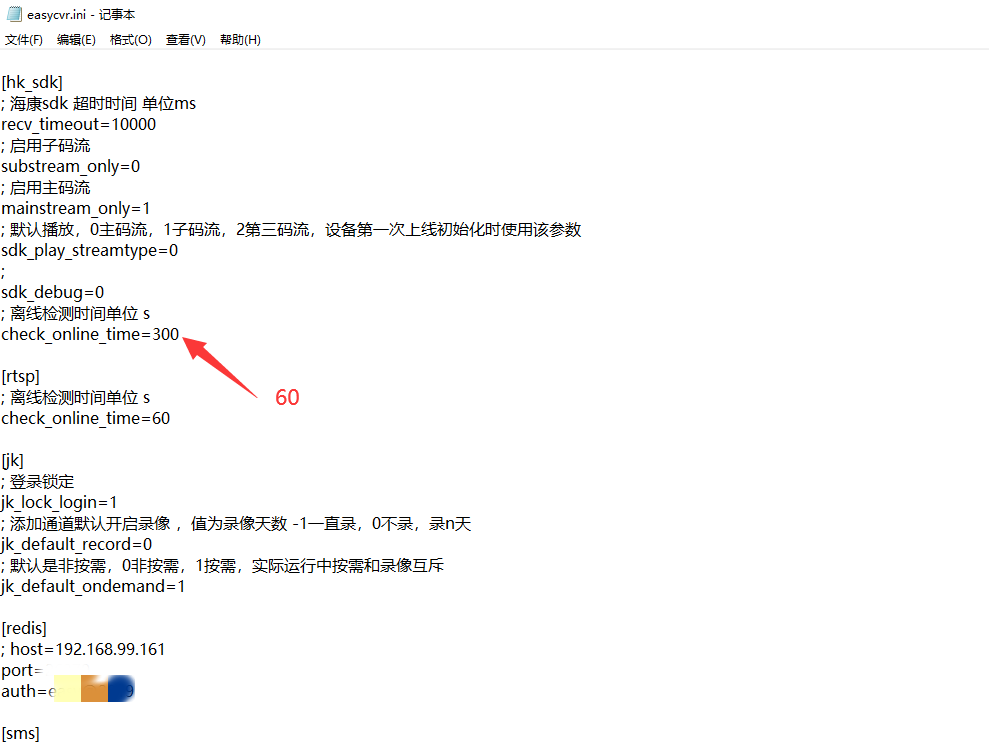
安防视频/集中云存储平台EasyCVR(V3.3)部分通道显示离线该如何解决?
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统安…...
软件测试经典面试题:如何进行支付功能的测试?
非现金支付时代,非现金支付已经成为了生活不可或缺的一部分,我们只需要一台手机便可走遍全国各地(前提是支付宝,微信有钱<00>),那么作为测试人员,支付测试也是非常重要的一环,那么下面我就…...
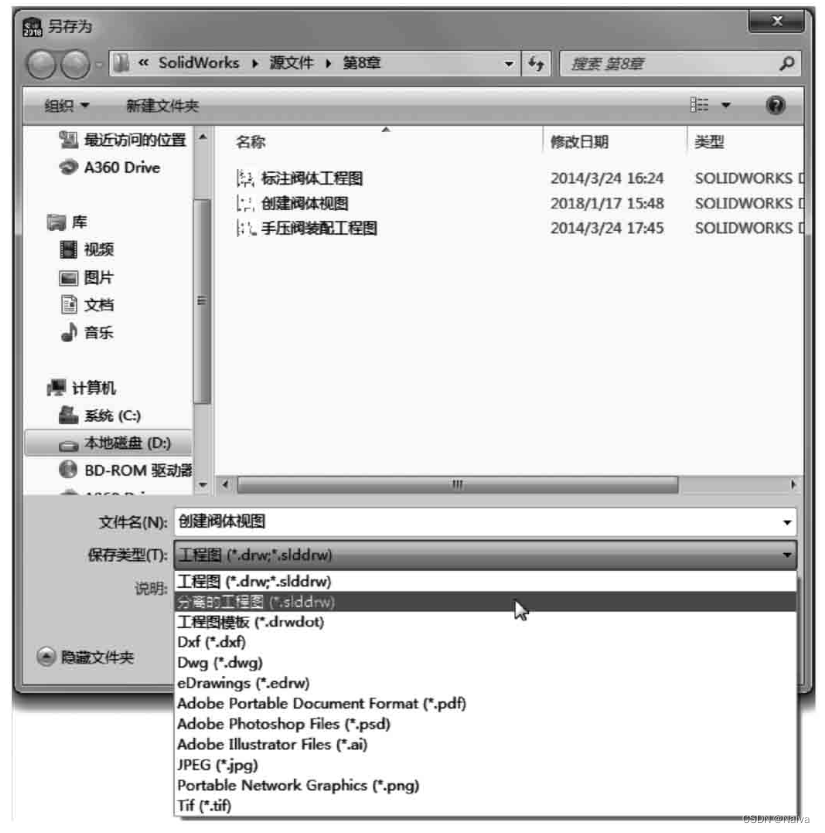
SolidWorks 入门笔记03:生成工程图和一键标注
默认情况下,SOLIDWORKS系统在工程图和零件或装配体三维模型之间提供全相关的功能,全相关意味着无论什么时候修改零件或装配体的三维模型,所有相关的工程视图将自动更新,以反映零件或装配体的形状和尺寸变化;反之&#…...
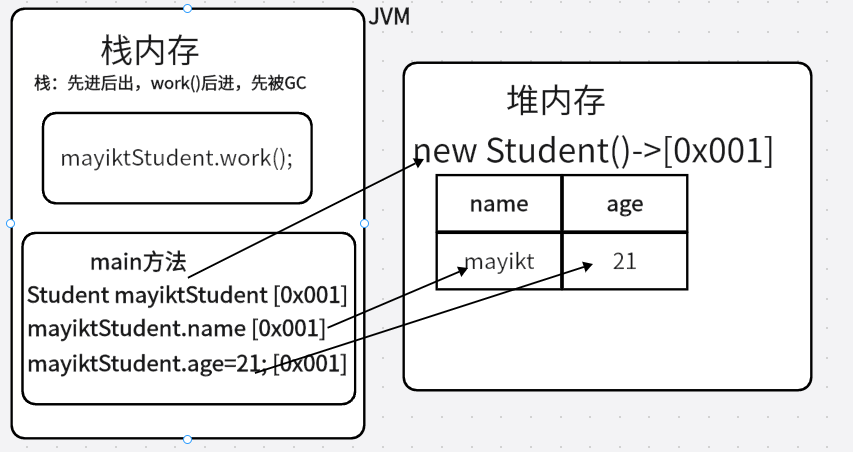
【Java】对象内存图多个对象同一内存地址
目录 学生类 单个对象内存图 多个对象指向同一个内存地址 学生类 Student.java如下: package com.面向对象;public class Student {String name;int age;public void work() {System.out.println("开始敲代码...");} }StudentDemo.java如下ÿ…...
)
Python 笔记05(装饰器的使用)
一 装饰器的使用 (property) property 是 Python 中用于创建属性的装饰器。它的作用是将一个类方法转换为类属性,从而可以像 访问属性一样访问该方法,而不需要使用函数调用的语法。使用 property 主要有以下好处: 封装性和隐藏实现细节&…...

记忆化搜索,901. 滑雪
901. 滑雪 - AcWing题库 给定一个 R 行 C 列的矩阵,表示一个矩形网格滑雪场。 矩阵中第 i行第 j 列的点表示滑雪场的第 i 行第 j列区域的高度。 一个人从滑雪场中的某个区域内出发,每次可以向上下左右任意一个方向滑动一个单位距离。 当然࿰…...

计算机网络:连接世界的纽带
计算机网络的基础概念 计算机网络是一组相互连接的计算机,它们通过通信链路和协议进行数据交换和资源共享。以下是一些关键概念: 1. 节点和主机 网络中的计算机设备称为节点,通常是主机或服务器。主机是普通用户或终端设备,而服…...
注解开发)
SpringMVC 学习(三)注解开发
4. 注解开发 4.1 环境搭建 (1) 新建 maven 模块 springmvc-03-annotation (2) 确认依赖 确认方法同 3(2),手动导入发布依赖见3(11) <!--资源过滤--> <build><resources><resource><directory>src/main/java</directory>&…...
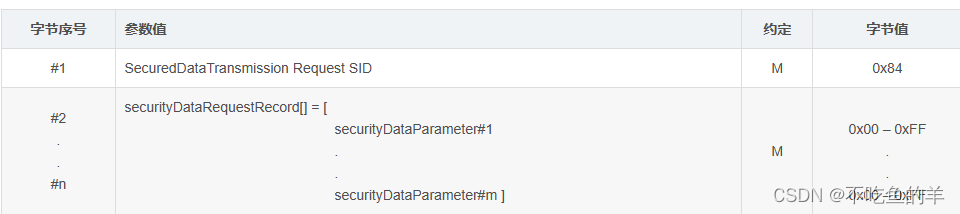
0x84加密数据传输服务
为了在安全模式下实现一些诊断服务,在服务端和客户端应用程序之间添加了Security sub-layer。在客户端与服务端之间进行诊断服务数据传输有两种方法: 1、非安全模式下数据传输 应用程序使用诊断服务(diagnostic Services)和应用层服务原语(Applicati…...

Vue.js快速入门:构建现代Web应用
Vue Vue.js是一款流行的JavaScript框架,用于构建现代的、交互式的Web应用程序。它具有简单易学的特点,同时也非常强大,能够帮助开发者构建高效、可维护的前端应用。本篇博客将带你快速入门Vue.js,并演示如何构建一个简单的Vue应用…...

Scala第五章节
Scala第五章节 scala总目录 章节目标 掌握方法的格式和用法掌握函数的格式和用法掌握九九乘法表案例 1. 方法 1.1 概述 实际开发中, 我们需要编写大量的逻辑代码, 这就势必会涉及到重复的需求. 例如: 求10和20的最大值, 求11和22的最大值, 像这样的需求, 用来进行比较的逻…...
)
erlang练习题(三)
题目一 查询列表A是否为列表B的前缀 解答 isPrefix([], List2) -> io:format("A is prefix of B ~n");isPrefix([H1 | ListA], [H2 | ListB]) ->case H1 H2 oftrue -> isPrefix(ListA, ListB);false -> io:format("A is not prefix of B ~n&quo…...

What Is A DNS Amplification DDoS Attack?
什么是 DNS 放大攻击? 域名系统 (DNS) 是用于在网站的机器可读地址(例如 191.168.0.1:80)和人类可读名称(例如 radware.com)之间进行解析的目录在 DNS 放大攻击中,攻击者…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
