leetCode 188.买卖股票的最佳时机 IV 动态规划 + 状态压缩
给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:k = 2, prices = [2,4,1] 输出:2 解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
示例 2:
输入:k = 2, prices = [3,2,6,5,0,3] 输出:7 解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
>>思路和分析
这道题目是 的进阶版,这里要求至多有k次交易
>>动规五部曲
1.确定dp数组以及下标的含义
一天 一共有 j 个 状态 ,dp[i][j] 中 i 表示 第 i 天,j 为[0 - 2*k] 个状态,dp[i][j]表示第 i 天状态 j所剩最大现金
- 0.没有操作(其实也可以不设置这个状态)
- 1.第一次持有股票
- 2.第一次不持有股票
- 3.第二次持有股票
- 4.第二次不持有股票
- ...
"持有" : 不代表就是当天"买入"!可能昨天就买入了,今天保持有的状态
- ① 我们可以发现,除了0以外,偶数就是不持有,奇数就是持有
- ② 题目要求是至多有k笔交易,那么j的范围就定义为 2*k+1就可以
vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
2.确定递推公式

同理类比剩下的状态,代码如下:
for (int j = 0; j < 2 * k - 1; j += 2) {dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}推导思路:
-----------------------------------------------------------
第 i 天 的五种状态
dp[i][0] 不操作dp[i][1] 第一天持有股票时剩下的最大金钱
dp[i][1] dp[i-1][1]dp[i-1][0] - prices[i]dp[i][2] 第一天不持有股票时剩下的最大金钱
dp[i][2] dp[i-1][2]dp[i-1][1] + prices[i]dp[i][3] 第二天持有股票时剩下的最大金钱
dp[i][3] dp[i-1][3]dp[i-1][2] - prices[i]
dp[i][4] 第二天不持有股票时剩下的最大金钱
dp[i][4] dp[i-1][4]dp[i-1][3] + prices[i]-----------------------------------------------------------
dp[i][j+1] dp[i-1][j+1]dp[i-1][j] - prices[i]dp[i][j+2] dp[i-1][j+2]dp[i-1][j+1] + prices[i]dp[i][j+1] = max(dp[i-1][j+1],dp[i-1][j] - prices[i]);
dp[i][j+2] = max(dp[i-1][j+2],dp[i-1][j+1] + prices[i]);
-----------------------------------------------------------3.dp数组初始化
dp[0][0] = 0;
dp[0][1] = -prices[0];
dp[0][2] = 0;
dp[0][3] = -prices[0];
dp[0][4] = 0;
...
同理推出dp[0][j],当 j 为奇数时都初始化为 -prices[0]。代码如下:
for (int j = 1; j < 2 * k; j += 2) {dp[0][j] = -prices[0];
}4.确定遍历顺序
从递归公式其实已经可以看出,一定是从前向后遍历,因为dp[i],依靠dp[i - 1]的数值。
5.举例推导dp数组
(1)以输入[1,2,3,4,5],k = 2为例

(2)以输入[3,3,5,0,0,3,1,4],k = 2为例
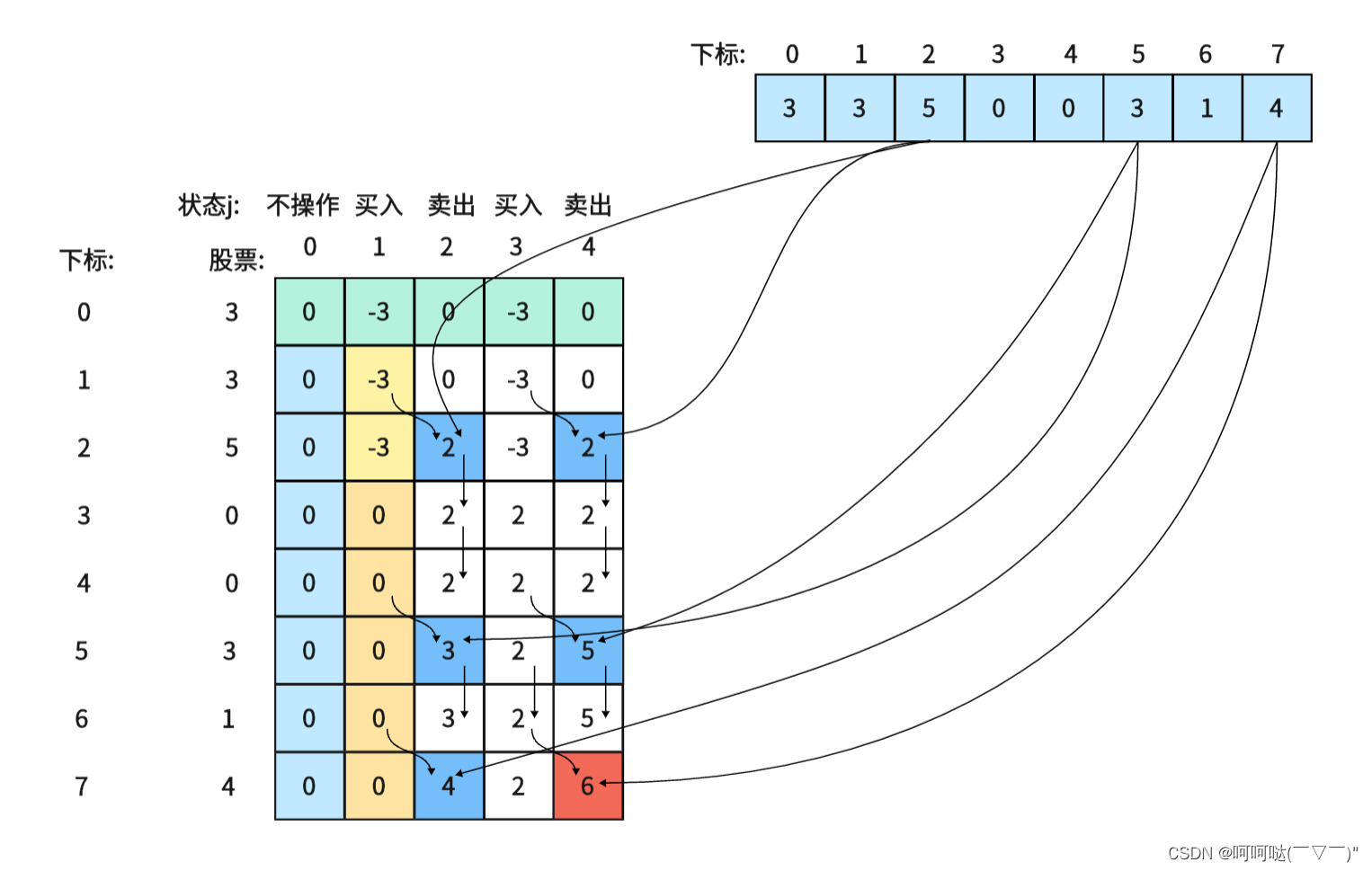
最后一次卖出,一定是利润最大的,dp[prices.size() - 1][2 * k]即红色部分就是最后求解。
class Solution {
public:int maxProfit(int k, vector<int>& prices) {if (prices.size() == 0) return 0;vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));for (int j = 1; j < 2 * k; j += 2) {dp[0][j] = -prices[0];}for (int i = 1;i < prices.size(); i++) {for (int j = 0; j < 2 * k - 1; j += 2) {dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);}}return dp[prices.size() - 1][2 * k];}
};- 时间复杂度: O(n * k),其中 n 为 prices 的长度
- 空间复杂度: O(n * k)
>>状态压缩
class Solution {
public:// 状态压缩int maxProfit(int k, vector<int>& prices) {if (prices.size() == 0) return 0;int len = prices.size();vector<int>dp(2 * k + 1,0);for(int j = 1;j < 2 * k;j += 2) {dp[j] = -prices[0];}for(int i=1;i<len;i++) {for(int j=0;j < 2*k-1;j += 2) {dp[j+1] = max(dp[j+1],dp[j] - prices[i]);dp[j+2] = max(dp[j+2],dp[j+1] + prices[i]);}}return dp[2*k];}
};- 时间复杂度: O(n * k),其中 n 为 prices 的长度
- 空间复杂度: O(k)
参考和推荐文章、视频
动态规划来决定最佳时机,至多可以买卖K次!| LeetCode:188.买卖股票最佳时机4_哔哩哔哩_bilibili
代码随想录 (programmercarl.com)
来自代码随想录课堂截图:

相关文章:

leetCode 188.买卖股票的最佳时机 IV 动态规划 + 状态压缩
给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。 设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。 注意:你不能同时参与多…...

Lua学习笔记:debug.sethook函数
前言 本篇在讲什么 使用Lua的debug.setHook函数 本篇需要什么 对Lua语法有简单认知 依赖Sublime Text工具 本篇的特色 具有全流程的图文教学 重实践,轻理论,快速上手 提供全流程的源码内容 ★提高阅读体验★ 👉 ♠ 一级标题 &…...

信息化发展74
产业数字化 产业数字化是指在新一代数字科技支撑和引领下,以数据为关键要素,以价值释放为核心,以数据赋能为主线,对产业链上下游的全要素数字化升级、转型和再造的过程。产业数字化作为实现数字经济和传统经济深度融合发展的重要…...
Go-Ldap-Admin | openLDAP 同步钉钉、企业微信、飞书组织架构实践和部分小坑
目录 一、Docker-compose快速拉起demo测试环境 二、原生部署流程 安装MySQL:5.7数据库 安装openLDAP 修改域名,新增con.ldif 创建一个组织 安装OpenResty 下载后端 下载前端 部署后端 部署前端 三、管理动态字段 钉钉 企业微信 飞书 四、…...
elasticsearch+logstash+kibana整合(ELK的使用)第一课
一、安装elasticsearch 0、创建目录,统一放到/data/service/elk 1、下载安装包 wget https://artifacts.elastic.co/downloads/elasticsearch/elasticsearch-7.1.0-linux-x86_64.tar.gz2、解压 tar -xzvf elasticsearch-7.1.0-linux-x86_64.tar.gz3、新建用户和组…...

宝塔 php修改了php.ini配置不生效
最近在使用hypref,php的版本是7.4 服务器linux,用宝塔安装完php,并装完swoole插件后 安装了swoole后,需要在php.ini中修改一下配置文件 添加 swoole.use_shortnameOff 但是添加了,重启php,依然不生效 解决方法是: 同时…...
)
Unrecognized option ‘stream_loop‘.(版本不匹配,利用make编译安装)
执行如下命令: ffmpeg -re -stream_loop -1 -i 1.mp4 -vcodec copy -acodec copy -f rtsp -rtsp_transport tcp rtsp://localhost:8554/live1.sdp报如下错误:Unrecognized option ‘stream_loop’. 查看ffmpeg版本:ffmpeg -version 显示&am…...

【考研数学】概率论与数理统计 —— 第三章 | 二维随机变量及其分布(2,常见的二维随机变量及二维变量的条件分布和独立性)
文章目录 引言四、常见的二维随机变量4.1 二维均匀分布4.2 二维正态分布 五、二维随机变量的条件分布5.1 二维离散型随机变量的条件分布律5.2 二维连续型随机变量的条件分布 六、随机变量的独立性6.1 基本概念6.2 随机变量独立的等价条件 写在最后 引言 有了上文关于二维随机变…...
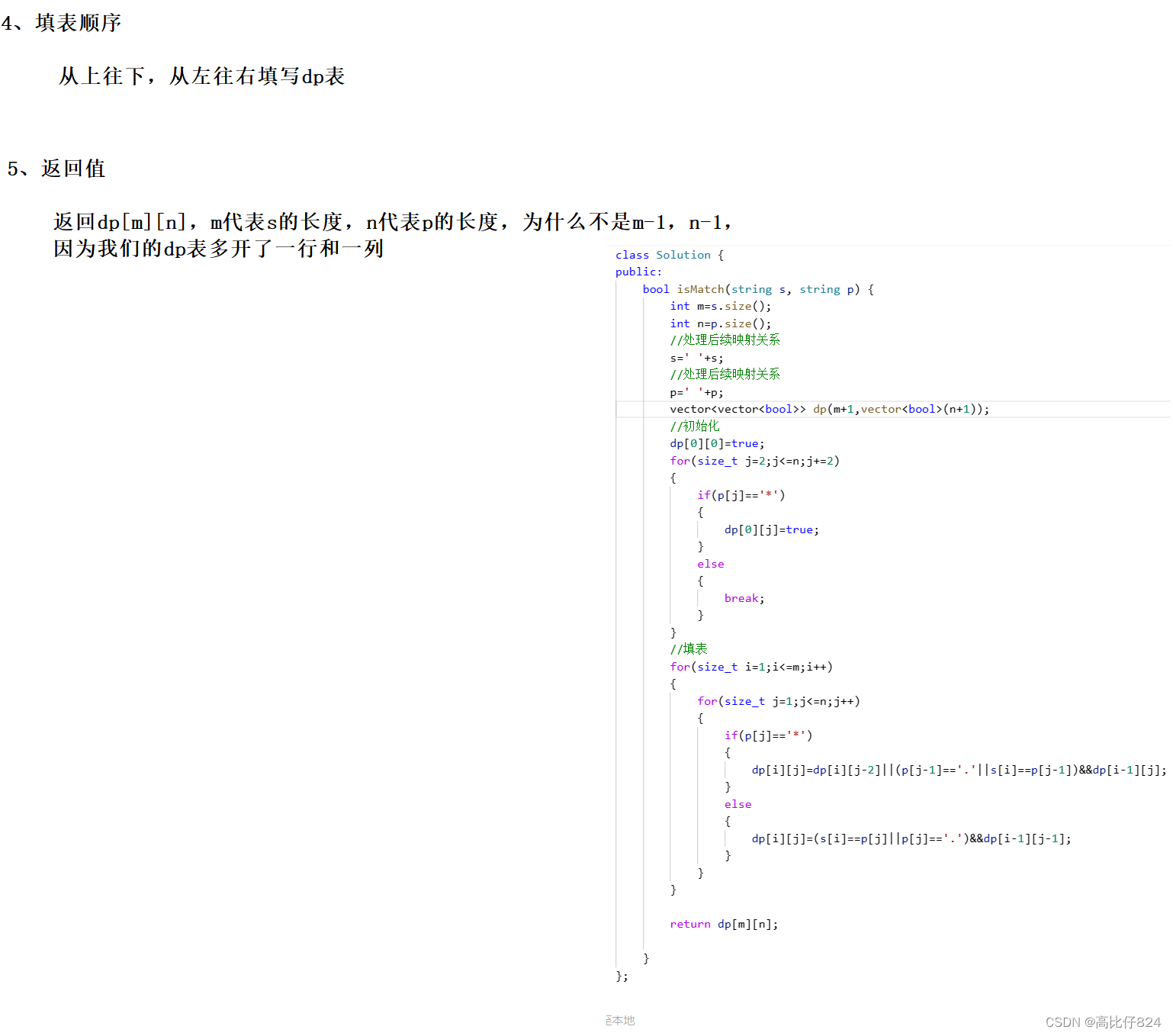
力扣 -- 10. 正则表达式匹配
解题步骤: 参考代码: class Solution { public:bool isMatch(string s, string p) {int ms.size();int np.size();//处理后续映射关系s s;//处理后续映射关系p p;vector<vector<bool>> dp(m1,vector<bool>(n1));//初始化dp[0][0]true…...
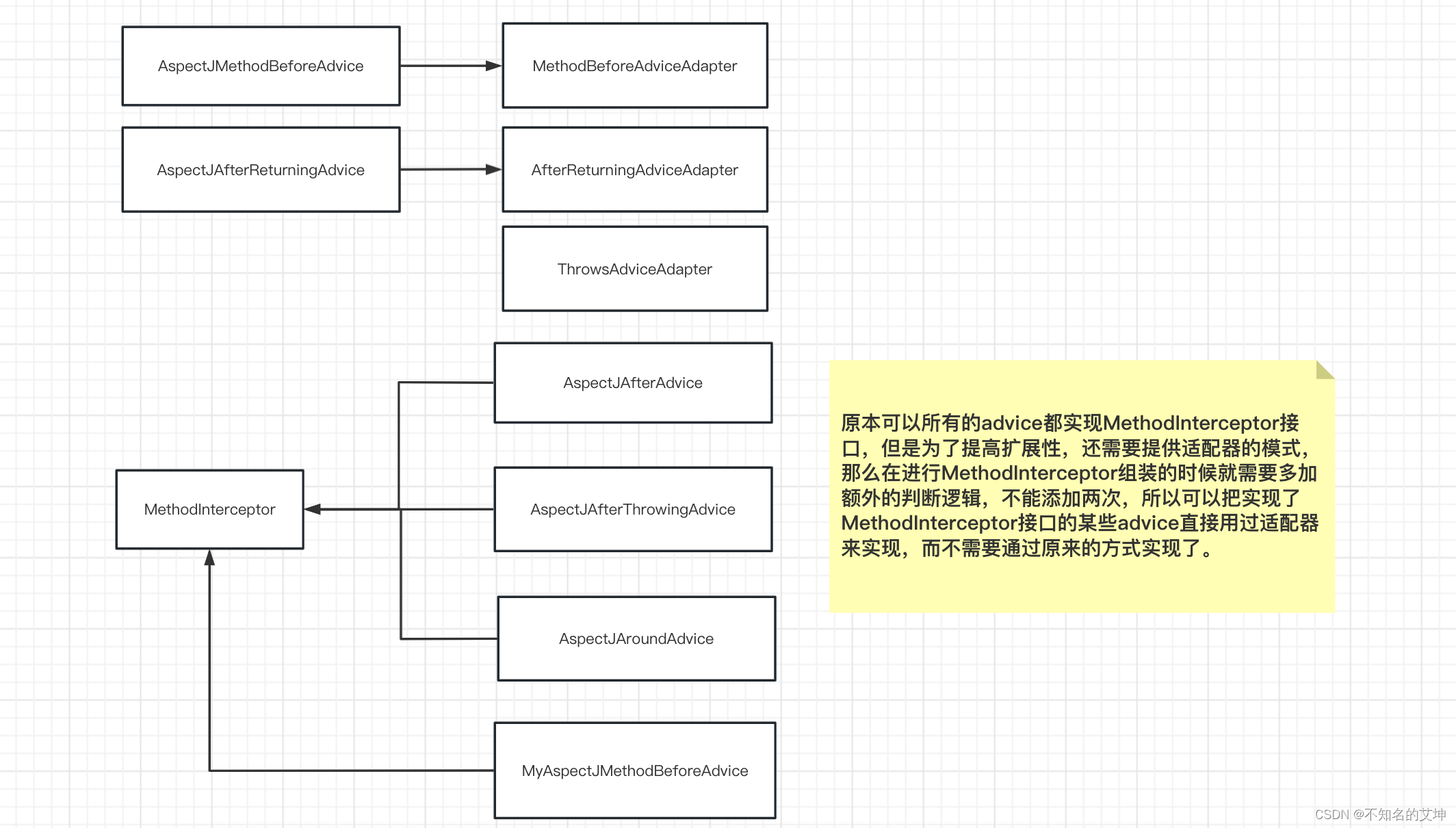
Spring源码分析(四) Aop全流程
一、Spring AOP基础概念 1、基础概念 连接点(Join point):能够被拦截的地方,Spring AOP 是基于动态代理的,所以是方法拦截的,每个成员方法都可以称之为连接点;切点(Poincut):每个方法都可以称之为连接点&…...

定义现代化实时数据仓库,SelectDB 全新产品形态全面发布
导读:9 月 25 日,2023 飞轮科技产品发布会在线上正式召开,本次产品发布会以 “新内核、新图景” 为主题,飞轮科技 CEO 马如悦全面解析了现代化数据仓库的演进趋势,宣布立足于多云之上的 SelectDB Cloud 云服务全面开放…...

Linux系统编程(七):线程同步
参考引用 UNIX 环境高级编程 (第3版)黑马程序员-Linux 系统编程 1. 同步概念 所谓同步,即同时起步、协调一致。不同的对象,对 “同步” 的理解方式略有不同 设备同步,是指在两个设备之间规定一个共同的时间参考数据库同步,是指让…...
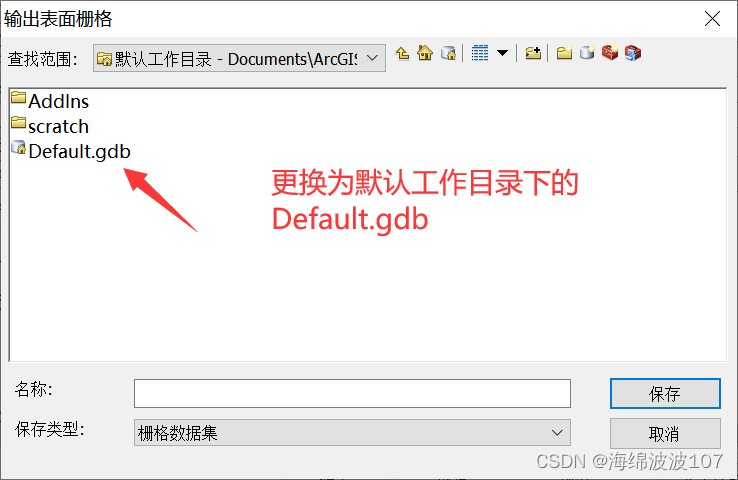
Arcgis克里金插值报错:ERROR 999999: 执行函数时出错。 表名无效。 空间参考不存在。 ERROR 010429: GRID IO 中存在错误
ERROR 999999: 执行函数时出错。 问题描述 表名无效。 空间参考不存在。 ERROR 010429: GRID IO 中存在错误: WindowSetLyr: Window cell size does not match layer cell size. name: c:\users\lenovo\appdata\local\temp\arc2f89\t_t164, adepth: 32, type: 1, iomode: 6, …...

【网络协议】ARP协议
为什么网络需要同时借助MAC地址这种物理地址和IP地址这种逻辑地址进行通信? 尽管目前MAC地址可以通过逻辑的方式进行修改,但它最初是被设计为不可人为更改的硬件地址。虽然MAC地址也可以满足唯一性的要求,但由于它不可由管理员根据需求通过逻…...
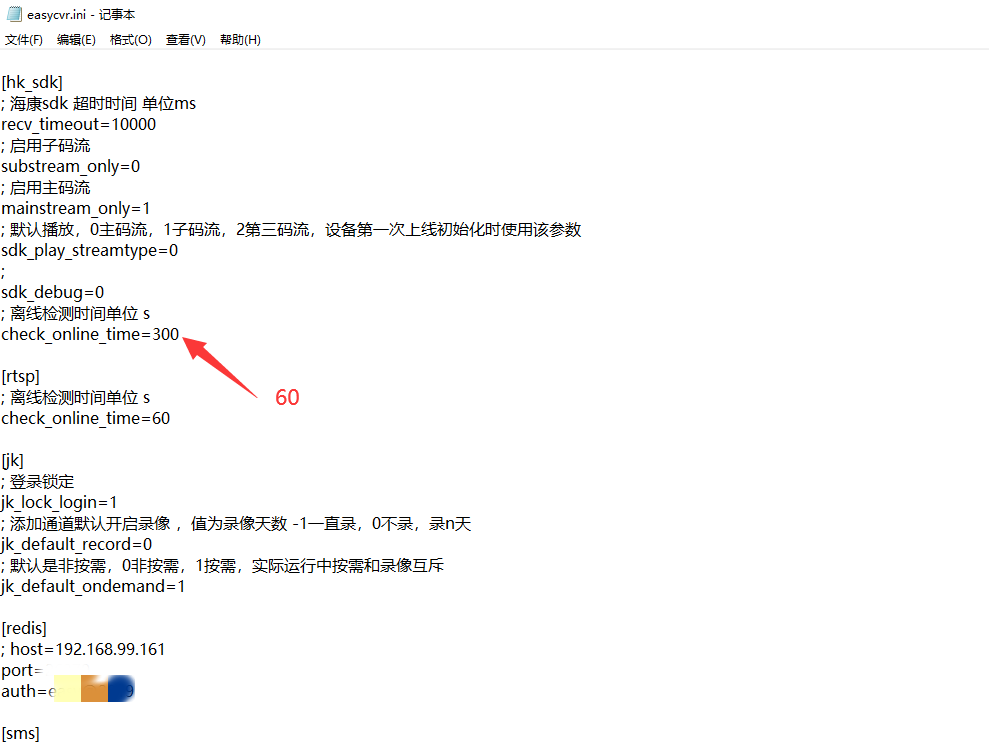
安防视频/集中云存储平台EasyCVR(V3.3)部分通道显示离线该如何解决?
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统安…...
软件测试经典面试题:如何进行支付功能的测试?
非现金支付时代,非现金支付已经成为了生活不可或缺的一部分,我们只需要一台手机便可走遍全国各地(前提是支付宝,微信有钱<00>),那么作为测试人员,支付测试也是非常重要的一环,那么下面我就…...
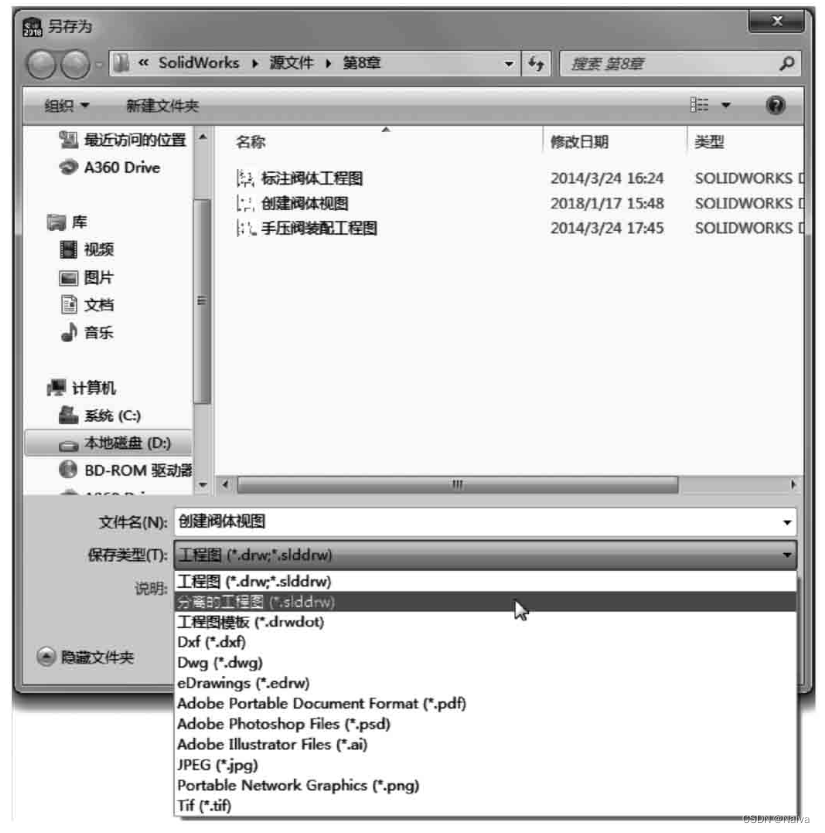
SolidWorks 入门笔记03:生成工程图和一键标注
默认情况下,SOLIDWORKS系统在工程图和零件或装配体三维模型之间提供全相关的功能,全相关意味着无论什么时候修改零件或装配体的三维模型,所有相关的工程视图将自动更新,以反映零件或装配体的形状和尺寸变化;反之&#…...
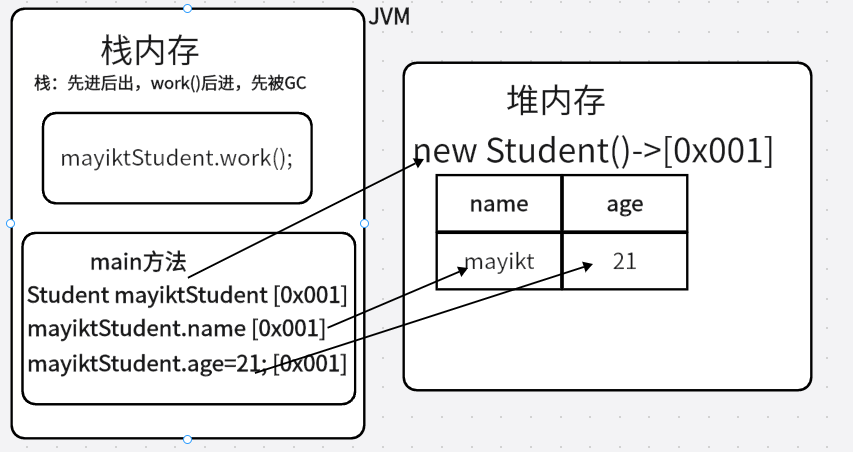
【Java】对象内存图多个对象同一内存地址
目录 学生类 单个对象内存图 多个对象指向同一个内存地址 学生类 Student.java如下: package com.面向对象;public class Student {String name;int age;public void work() {System.out.println("开始敲代码...");} }StudentDemo.java如下ÿ…...
)
Python 笔记05(装饰器的使用)
一 装饰器的使用 (property) property 是 Python 中用于创建属性的装饰器。它的作用是将一个类方法转换为类属性,从而可以像 访问属性一样访问该方法,而不需要使用函数调用的语法。使用 property 主要有以下好处: 封装性和隐藏实现细节&…...

记忆化搜索,901. 滑雪
901. 滑雪 - AcWing题库 给定一个 R 行 C 列的矩阵,表示一个矩形网格滑雪场。 矩阵中第 i行第 j 列的点表示滑雪场的第 i 行第 j列区域的高度。 一个人从滑雪场中的某个区域内出发,每次可以向上下左右任意一个方向滑动一个单位距离。 当然࿰…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
