动态规划算法(1)--矩阵连乘和凸多边形剖分
目录
一、动态数组
1、创建动态数组
2、添加元素
3、删除修改元素
4、访问元素
5、返回数组长度
6、for each遍历数组
二、输入多个数字
1、正则表达式
2、has.next()方法
三、矩阵连乘
1、什么是矩阵连乘?
2、动态规划思路
3、手推m和s矩阵
4、完整代码
5、备忘录方法
四、凸多边形剖分
1、凸多边形形三角剖分原理
2、完整代码
一、动态数组
1、创建动态数组
创建动态数组ArrayList,先调用ArrayList库,之后动态创建语句如下,括号内填写数组元素个数,不知道可以不填。
import java.util.ArrayList;ArrayList<Integer> num = new ArrayList<>();2、添加元素
使用函数add添加元素。如:添加元素1。
num.add(1);如果创建一个ArrayList num与list1相同(num和list1同为ArrayList类型)
ArrayList<Integer> num = new ArrayList<>(list1);3、删除修改元素
使用函数remove删除特定索引的元素。如:删除索引为1的元素。
num.remove(1);使用函数set修改特定索引的元素。如:将索引为1的元素修改为"java"。
num.set(1,"java");4、访问元素
使用函数get返回特定索引的元素。如:返回索引1的元素并打印。
system.out.println(num.get(1));5、返回数组长度
使用函数size()返回数组长度。如:返回数组num长度并打印
system.out.println(num.size())6、for each遍历数组
i是遍历的数组每一个值,num是数组名。
for(int i:num){System.out.println(i);}二、输入多个数字
1、正则表达式
不需要import其他的东西。输入一串以空格为间隔的数字,字符串形式,经过正则表达式拆解,存入num动态数组中。
如果数字之间以逗号为间隔,则需要将匹配改为",\\s+"。
import java.util.ArrayList;ArrayList<Integer> num = new ArrayList<>();String input= new Scanner(System.in).nextLine();String[] numbers=input.split("\\s+");for (String number : numbers) {num.add(Integer.parseInt(number));}2、has.next()方法
该方法存在弊端,不能退出循环。
import java.util.ArrayList;ArrayList<Integer> num = new ArrayList<>();Scanner scanner=new Scanner(System.in);int n;int[] num;while(scanner.hasNext()) {n=scanner.nextInt();num.add(n);}三、矩阵连乘
1、什么是矩阵连乘?
不同的结合方式,可以导致不同的数乘次数,因为乘法远大于加法量级,所以加法可以忽视。那什么样的括号选择是可以获得最少的数乘次数呢?

如果一味的进行枚举,寻找最优的数乘次数需要指数级复杂度。显然这种方式,在较大的个数面前利用计算机是不能解决的。

2、动态规划思路
(1)首先定义几个结构,以便后续进行理解。
A[1:n],代表1到n个矩阵的连乘积。
A[i:j]的最少数乘次数记为m[i][j]。
p数组为矩阵链的值。比如30*35和35*15两个矩阵的矩阵链为30,35,15。
s数组记录断开位置。
(2)矩阵连乘遵循最优子结构,也就是说矩阵连乘的各子结构都是最优的。
假设A[1:4]的最优子结构是 ,那么A[1:2]的最优子结构一定是
。
根据上面两条,我们能得出A[i:j]的最少数乘次数记为m[i][j],

3、手推m和s矩阵
m矩阵和s矩阵几乎同步计算,仅保留上三角形,主对角线均为全0,依次按对角线进行计算,每计算完一条对角线向右上平移一条对角线。

下面给出m[1][3]和s[1][3]的计算,可以看到从1断开()小于从2分割(
)的值,所以m[1][3]选择较小者7875,s[1][3]=1。

如果求解A[1:6]的最优解的匹配方式,倒序执行上面s步骤。
4、完整代码
import java.util.Scanner;
import java.util.ArrayList;
public class matrixplusnew {public static void main(String[] args){ArrayList<Integer> num = new ArrayList<>();String input= new Scanner(System.in).nextLine();String[] numbers=input.split("\\s+");for (String number : numbers) {num.add(Integer.parseInt(number));}int size=num.size()-1;//6*6int [][] m=new int[size+1][size+1];int [][] s=new int[size+1][size+1];MatrixChain(num,m,s);//输出m数组for(int i=1;i<size+1;i++){for(int j=1;j<size+1;j++){System.out.print(m[i][j]);System.out.print("\t");}System.out.println("");}//输出s数组for(int i=1;i<size+1;i++){for(int j=1;j<size+1;j++){System.out.print(s[i][j]);System.out.print("\t");}System.out.println("");}//输出A[1:6]的匹配方式Traceback(1, 6, s);}//m数组和s数组生成public static void MatrixChain(ArrayList<Integer>p,int [][]m,int [][]s) {int n = p.size() - 1;for (int i = 1; i <= n; i++) {m[i][i] = 0;}for (int r = 2; r <= n; r++) {for (int i = 1; i <= n - r + 1; i++) {int j = i + r - 1; //这个位置非常巧妙,可以确保对角线依次执行m[i][j] = m[i + 1][j] + p.get(i - 1) * p.get(i) * p.get(j);//由于第二条对角线,依赖于第一条对角线计算m[i][i],m[i][i]值为0,故省略。s[i][j] = i;for (int k = i + 1; k < j; k++){int t = m[i][k] + m[k + 1][j] + p.get(i - 1) * p.get(k) * p.get(j);if (t < m[i][j]) {m[i][j] = t;s[i][j] = k;}}}}}//获得括号匹配方式private static void Traceback(int i,int j,int[][]s){if(i==j)return;Traceback(i, s[i][j],s); //单独写每两个子结构的最优解,可以供读者合成匹配方式Traceback(s[i][j]+1,j,s);System.out.print("A"+i+", "+s[i][j]);System.out.println(" and A"+(s[i][j]+1)+", "+j);}
}
5、备忘录方法
备忘录算法自顶向下计算,但他不够灵活,每次计算完整矩阵链的最优次序。其中p,m数组都为类外数组,所有函数均可使用。通过减少重复计算,减少时间复杂度。

public static int memoizedmatrixChain(int n){for (int i=0;i<=n;i++){for(int j=0;j<=n;j++){m[i][j]=0;}}//初始化备忘录数组return lookupChain(1,n);
}
public static lookupChain(int i,int j){if(m[i][j]>0)return m[i][j];//如果该项子问题有记录,返回该记录if(i==j)return 0;//如果相乘的两个矩阵相等,则返回0int u=lookupChain(i+1,j)+p[i-1]*p[i]p[j];//递归调用s[i][j]=i;//存储最佳断点for(int k=i+1;k<j;k++){//这里面将断点从i+1开始,可以断链的点直到j-1为止int t=lookupChain(i,k)+lookupChain(k+1,j)+p[i-1]*p[k]*p[j];if(t<u){u=t;s[i][j]=k;}}m[i][j]=u;return u;
}
四、凸多边形剖分
凸多边形三角剖分问题类似于矩阵连乘,都是利用动态规划分成子问题,对子问题递归求解。
1、凸多边形形三角剖分原理
通过不同的拆分方法,假设不同边有不同的权值,那么或者不同的组合方式有不同的函数映射,那么不同的三角剖分方式就会存在不同的解,那么最优解怎么求呢?

类比于矩阵连乘的规律,我们也对不同的组合方式加括号表示。最后凸多边形剖分问题也表示为多个子问题叠加的解。

那么根据矩阵连乘,有下面这种最优解的产生形式,可以根据不同的加权的关系写出函数关系,变成矩阵连乘问题。
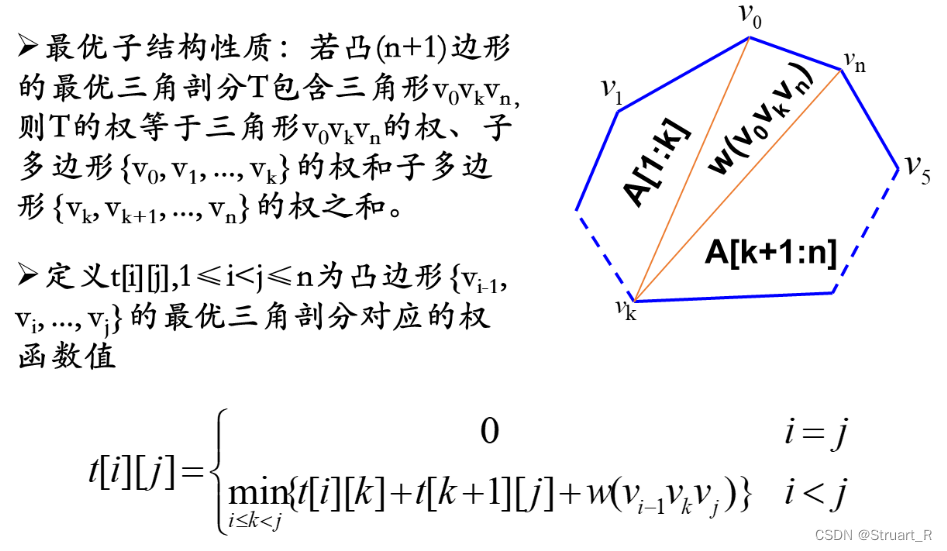
2、完整代码
public class MinWeightTriangulation {public static void main(String [] args){int size=5;int m[][]=new int[size+1][size+1];int s[][]=new int[size+1][size+1];//定义权值int num[][]= {{0,2,2,3,1,4},{2,0,1,5,2,3},{2,1,0,2,1,4},{3,5,2,0,6,2},{1,2,1,6,0,1},{4,3,4,2,1,0}};Triangle(num,m,s);for(int i=1;i<size+1;i++){for(int j=1;j<size+1;j++){System.out.print(m[i][j]);System.out.print("\t");}System.out.println("");}Traceback(1, 5, s);}//计算最优值public static void Triangle(int[][]num,int[][]m,int[][]s){int n=5;for(int i=1;i<=n;i++)m[i][i]=0;for(int r=2;r<=n;r++){for(int i=1;i<=n-r+1;i++){int j=i+r-1;m[i][j]=m[i+1][j]+Weight(i-1, i, j, num);s[i][j]=i;for(int k=i+1;k<j;k++){int t=m[i][k]+m[k+1][j]+Weight(i-1, k, j, num);if(t<m[i][j]){m[i][j]=t;s[i][j]=k;}}}}}//权重计算public static int Weight(int i,int j,int k,int[][]num){return num[i][j]+num[j][k]+num[i][k];}//返回匹配方式public static void Traceback(int i,int j,int[][]s){if(i==j)return;Traceback(i, s[i][j],s);Traceback(s[i][j]+1,j,s);System.out.print("A"+i+", "+s[i][j]);System.out.println(" and A"+(s[i][j]+1)+", "+j);}
}
相关文章:

动态规划算法(1)--矩阵连乘和凸多边形剖分
目录 一、动态数组 1、创建动态数组 2、添加元素 3、删除修改元素 4、访问元素 5、返回数组长度 6、for each遍历数组 二、输入多个数字 1、正则表达式 2、has.next()方法 三、矩阵连乘 1、什么是矩阵连乘? 2、动态规划思路 3、手推m和s矩阵 4、完…...

通过Nginx重新认识HTTP错误码
文章目录 概要一、HTTP错误码1.1、1xx1.2、2xx1.3、3xx1.4、4xx1.5、5xx 二、Nginx对常见错误处理三、参考资料 概要 在web开发过程中,通过HTTP错误码快速定位问题是一个非常重要的技能,同时Nginx是非常常用的一个实现HTTP协议的服务,因此本…...

某房产网站登录RSA加密分析
文章目录 1. 写在前面2. 抓包分析3. 扣加密代码4. 还原加密 1. 写在前面 今天是国庆节,首先祝福看到这篇文章的每一个人节日快乐!假期会老的这些天一直在忙事情跟日常带娃,抽不出一点时间来写东西。夜深了、娃也睡了。最近湖南开始降温了&…...
深度学习:基于长短时记忆网络LSTM实现情感分析
目录 1 LSTM网络介绍 1.1 LSTM概述 1.2 LSTM网络结构 1.3 LSTM门机制 1.4 双向LSTM 2 Pytorch LSTM输入输出 2.1 LSTM参数 2.2 LSTM输入 2.3 LSTM输出 2.4 隐藏层状态初始化 3 基于LSTM实现情感分析 3.1 情感分析介绍 3.2 数据集介绍 3.3 基于pytorch的代码实现 3…...
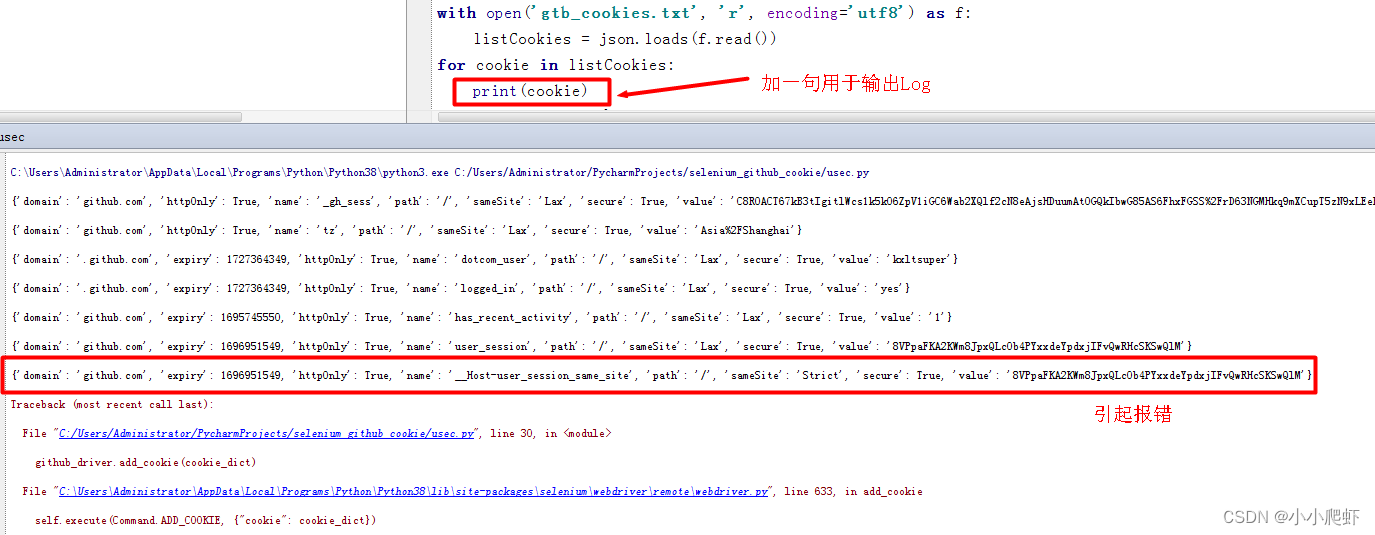
selenium使用已经获取的cookies登录网站报错unable to set cookie的处理方式
用selenium半手动登录github获取其登录cookies后,保存到一个文件gtb_cookies.txt中。 然后用selenium使用这个cookies文件,免登录上github。但是报错如下:selenium.common.exceptions.UnableToSetCookieException: Message: unable to set co…...
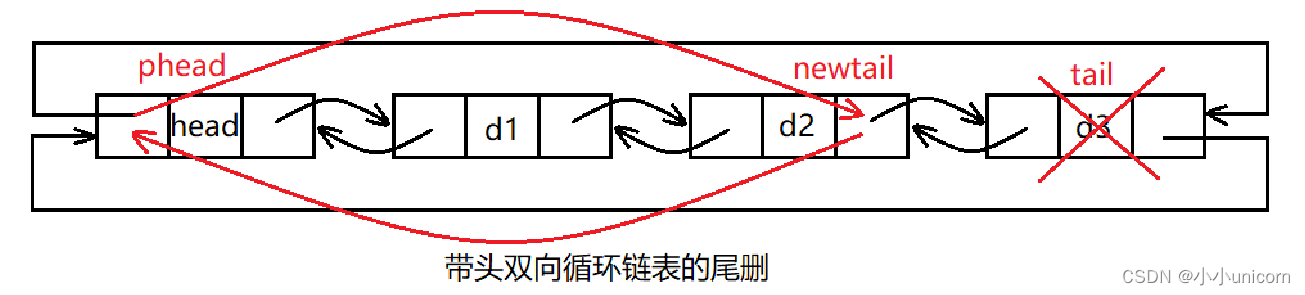
初阶数据结构(四)带头双向链表
💓博主csdn个人主页:小小unicorn ⏩专栏分类:数据结构 🚚代码仓库:小小unicorn的代码仓库🚚 🌹🌹🌹关注我带你学习编程知识 带头双向链表 链表的相关介绍初始化链表销毁链…...
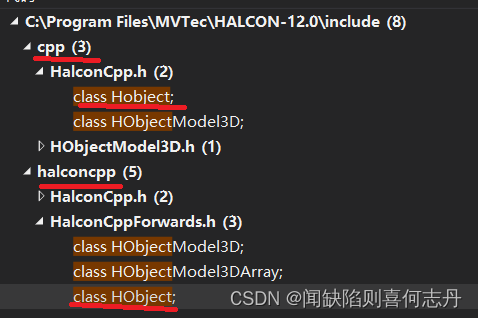
2022年9月及10月
9月 1.Halcon12的HObject和Hobject halcon12 可以用HObject,也可以用Hobject,用法都一样 包括HalconCpp.h 如果附加目录中: C:\Program Files\MVTec\HALCON-12.0\include\halconcpp\ 在前面,则用 HalconCpp::HObject 如果附加目录…...

Vmware安装
title: “Vmware安装” createTime: 2021-11-22T09:53:2908:00 updateTime: 2021-11-22T09:53:2908:00 draft: false author: “name” tags: [“VMware”,“安装”,“linux”] categories: [“install”] description: “测试的” linux安装VMware Workstation16 1.安装包 …...

RSA算法
算法简介 RSA是一种非对称加密方式。发送者把明文通过公钥加密后发送出去,接受者把密文通过私钥解密得到明文。 算法过程 生成公钥和私钥 选取两个质数p和q,np*q。n的长度就是密钥长度。φ(n)(p-1)*(q-1)φ(n)为n的欧拉函数。找到1-φ(n)间与φ(n)互质的…...

计算机竞赛 深度学习手势识别 - yolo python opencv cnn 机器视觉
文章目录 0 前言1 课题背景2 卷积神经网络2.1卷积层2.2 池化层2.3 激活函数2.4 全连接层2.5 使用tensorflow中keras模块实现卷积神经网络 3 YOLOV53.1 网络架构图3.2 输入端3.3 基准网络3.4 Neck网络3.5 Head输出层 4 数据集准备4.1 数据标注简介4.2 数据保存 5 模型训练5.1 修…...

Spring的Ordered
Ordered Java中的Ordered接口是Spring框架中的一个接口,用于表示对象的顺序。它定义了一个方法getOrder(),用于获取对象的顺序值,值越小的对象越先被处理。 Ordered接口是Spring框架中的一个接口,用于定义组件的加载顺序。当一个…...

前端两年半,CSDN创作一周年
文章目录 一、机缘巧合1.1、起因1.2、万事开头难1.3、 何以坚持? 二、收获三、日常四、憧憬 五、总结 一、机缘巧合 1.1、起因 最开始接触CSDN,还是因为同专业的同学,将计算机实验课的实验题,记录总结并发在了专业群里。后来正式…...

定时任务管理平台青龙 QingLong
一、关于 QingLong 1.1 QingLong 介绍 青龙面板是支持 Python3、JavaScript、Shell、Typescript 多语言的定时任务管理平台,支持在线管理脚本和日志等。其功能丰富,能够满足大部分需求场景,值得一试。 主要功能 支持多种脚本语言…...

java多线程相关介绍
1. 线程的创建和启动 在 Java 中创建线程有两种方式。一种是继承 Thread 类并重写其中的 run() 方法,另一种是实现 Runnable 接口并重写其中的 run() 方法。创建完线程对象后,调用 start() 方法可以启动线程。 2. 线程的状态 Java 的线程在不同阶段会处于…...

css复合选择器
交集选择器 紧紧挨着 <template><div><p class"btn">Click me</p><button class"btn" ref"myButton" click"handleClick">Click me</button></div> </template> <style> but…...
USART串口协议
通信接口 •通信的目的:将一个设备的数据传送到另一个设备,扩展硬件系统 • 通信协议:制定通信的规则,通信双方按照协议规则进行数据收发 全双工:指通信双方能够同时进行双向通信,一般来说,全双…...

picoctf_2018_shellcode
picoctf_2018_shellcode Arch: i386-32-little RELRO: Partial RELRO Stack: No canary found NX: NX disabled PIE: No PIE (0x8048000) RWX: Has RWX segments32位,啥都没开 这个看着挺大的,直接来个ROPchain,…...
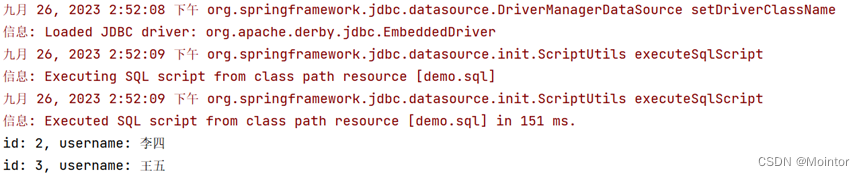
Apache Derby的使用
Apache Derby是关系型数据库,可以嵌入式方式运行,也可以独立运行,当使用嵌入式方式运行时常用于单元测试,本篇我们就使用单元测试来探索Apache Derby的使用 一、使用IDEA创建Maven项目 打开IDEA创建Maven项目,这里我…...

leetcode 图相关的题
图 图相关知识有leetcode207课程表1(有环判断)以及210 课程表2(拓扑排序). 链表遍历 def dfs(n):print(n)dfs(n)二叉树遍历 def dfs(n):print(n)dfs(n.left)dfs(n.right)多叉树遍历 dfs(root) def dfs(n):for node in n.nodes:dfs(node)图遍历 visited [False] * n_node…...

程序员们,我们能工作到65岁吗?
软件开发人员的职业生涯可以持续多久?这是大多数认真考虑成为专业程序员的人不禁想知道的事情。 在谈论这样一个要求很高的职业时,这是一个非常自然的问题。没有人愿意花费数年时间学习一项技能,这些技能将在几年内不再相关,或者当…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...
