C++简单实现AVL树
目录
一、AVL树的概念
二、AVL树的性质
三、AVL树节点的定义
四、AVL树的插入
4.1 parent的平衡因子为0
4.2 parent的平衡因子为1或-1
4.3 parent的平衡因子为2或-2
4.3.1 左单旋
4.3.2 右单旋
4.3.3 先左单旋再右单旋
4.3.4 先右单旋再左单旋
4.4 插入节点完整代码:
五、AVL树判断是否平衡
六、AVL树的验证
一、AVL树的概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查
找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii
和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
二、AVL树的性质
1、空树也是一颗AVL树
2、它的左右子树都是AVL树
3、左右子树高度差(平衡因子)的绝对值不超过1
4、如果一颗二叉搜索树是高度平衡的,它就是AVL树。如果它由N个节点,其高度可保持在O(log2N),搜索时间复杂度为O(log2N)。

三、AVL树节点的定义
template<class K, class V>
struct AVLTreeNode
{AVLTreeNode(const pair<K, V>& kv):_kv(kv),_parent(nullptr),_left(nullptr),_right(nullptr),_bf(0)//平衡因子初始为0{}pair<K, V> _kv;AVLTreeNode* _parent;AVLTreeNode* _left;AVLTreeNode* _right;int _bf;//平衡因子 —— balance factor
};四、AVL树的插入
AVL树的插入分为两大步:
1、新建节点,插入到正确的位置(使之符合二叉搜索树的性质)
如果插入到右边,则平衡因子加1,如果插入到左边,平衡因子减1;
2、判断平衡因子是否合法,不合法则调整节点(旋转)
插入完成后平衡因子有以下几种情况:
4.1 parent的平衡因子为0
如果此时parent的平衡因子为0,那么之前的平衡因子是1或-1,这棵树的高度不会变,不用向上更新,插入完成。
4.2 parent的平衡因子为1或-1
如果此时parent的平衡因子为1或-1,那么之前的平衡因子为0,高度改变了,需要向上更新。
4.3 parent的平衡因子为2或-2
如果此时parent的平衡因子为2或-2,那么需要通过旋转调平衡。
4.3.1 左单旋
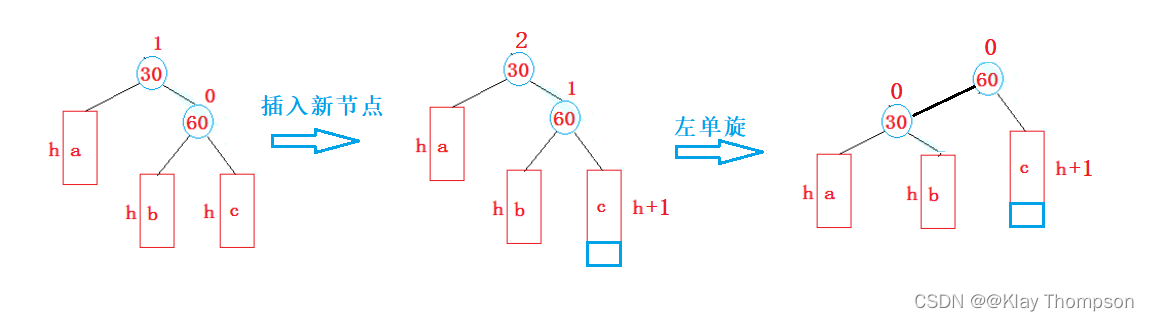
void RotateL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;cur->_left = parent;if (curleft)curleft->_parent = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){cur->_parent = nullptr;_root = cur;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;//更新平衡因子}4.3.2 右单旋

void RotateR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;cur->_right = parent;if (curright)curright->_parent = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){cur->_parent = nullptr;_root = cur;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}4.3.3 先左单旋再右单旋
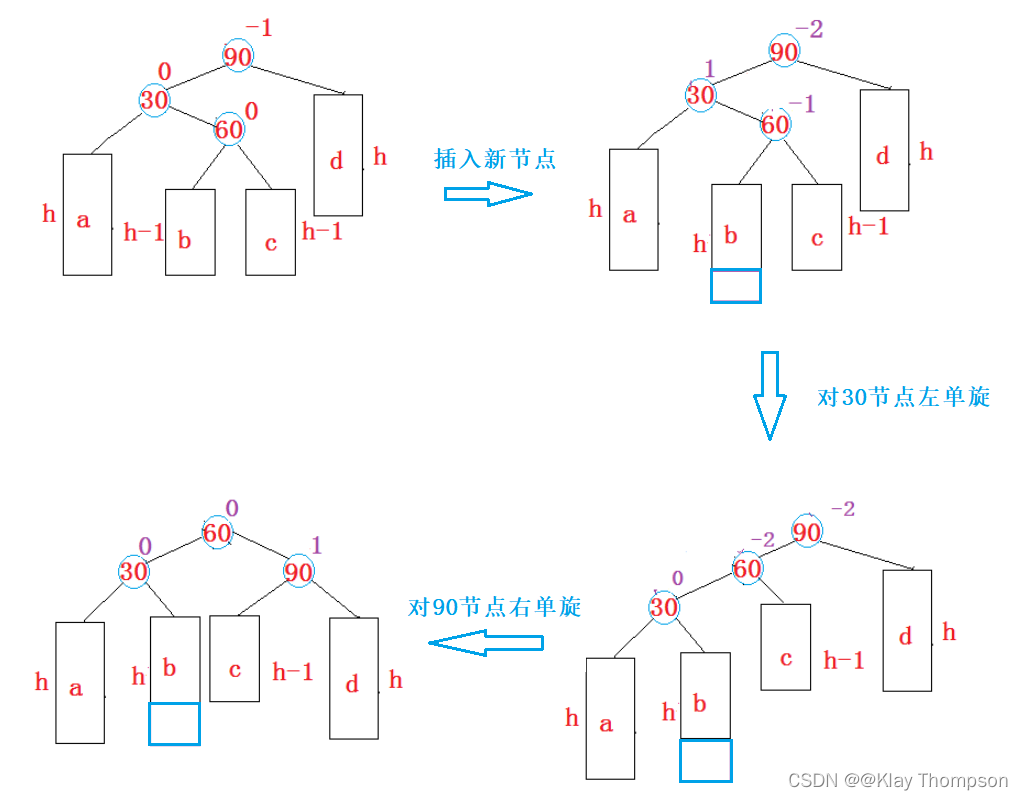
void RotateLR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;RotateL(parent->_left);RotateR(parent);//更新平衡因子if (bf == 0){parent->_bf = curright->_bf = cur->_bf = 0;}else if (bf == 1){parent->_bf = 0;cur->_bf = -1;curright = 0;}else if (bf == -1){parent->_bf = 1;cur->_bf = 0;curright = 0;}else{assert(false);}}4.3.4 先右单旋再左单旋
void RotateRL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf;RotateR(parent->_right);RotateL(parent);//更新平衡因子if (bf == 0){parent->_bf = curleft->_bf = cur->_bf = 0;}else if (bf == 1){parent->_bf = -1;cur->_bf = 0;curleft = 0;}else if (bf == -1){parent->_bf = 0;cur->_bf = 1;curleft = 0;}else{assert(false);}}4.4 插入节点完整代码:
bool insert(const pair<K, V>& kv){//如果root为空if (_root == nullptr){_root = new Node(kv);return true;}//插入Node* cur = _root;Node* parent = cur;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//刚开始忘记写了//插入完成,开始判断是否平衡//最坏走到根就不再判断了,根的parent为空while (parent){//更新平衡因子if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}//如果此时parent的平衡因子为0,那么之前的平衡因子是1或-1,这棵树的高度不会变,不用向上更新if (parent->_bf == 0){break;}//如果此时parent的平衡因子为1或-1,那么之前的平衡因子为0,高度改变了,需要向上更新else if (parent->_bf == 1 || parent->_bf == -1){//向上更新cur = parent;parent = parent->_parent;}//如果此时parent的平衡因子为2或-2,那么需要通过旋转调平衡else if (parent->_bf == 2 || parent->_bf == -2){//左单旋if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}//右单旋if(parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//先右单旋,再左单旋if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}//先左单旋,再右单旋if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}break;//忘记写了}else{assert(false);}}return true;}五、AVL树判断是否平衡
bool isBalance(){return _isBalance(_root);}int Height(Node* root){if (root == nullptr)return 0;int lh = Height(root->_left);int rh = Height(root->_right);return lh > rh ? lh + 1 : rh + 1;}bool _isBalance(Node* root){if (root == nullptr)return true;int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);int diff = abs(rightHeight - leftHeight);return diff <= 1 && _isBalance(root->_left) && _isBalance(root->_right);}六、AVL树的验证
int main()
{//常规场景AVLTree<int, int>* root1 = new AVLTree<int, int>();int a1[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };for (auto e : a1){root1->insert(make_pair(e, e));}root1->InOrder();cout << "isBalance: " << root1->isBalance() << endl;//特殊场景AVLTree<int, int>* root2 = new AVLTree<int, int>();int a2[] = { 4,2,6,1,3,5,15,7,16,14 };for (auto e : a2){root2->insert(make_pair(e, e));}root2->InOrder();cout << "isBalance: " << root2->isBalance() << endl;//随机数const int N = 100000;vector<int> v;v.reserve(N);srand(time(0));for (int i = 0; i < N; i++){int n = rand();v.push_back(n);}AVLTree<int, int>* root3 = new AVLTree<int, int>();for (auto e : v){root3->insert(make_pair(e, e));}//root->InOrder();cout << "isBalance: " << root3->isBalance() << endl;return 0;
}运行结果:

相关文章:

C++简单实现AVL树
目录 一、AVL树的概念 二、AVL树的性质 三、AVL树节点的定义 四、AVL树的插入 4.1 parent的平衡因子为0 4.2 parent的平衡因子为1或-1 4.3 parent的平衡因子为2或-2 4.3.1 左单旋 4.3.2 右单旋 4.3.3 先左单旋再右单旋 4.3.4 先右单旋再左单旋 4.4 插入节点完整代码…...
UE4 Cesium 与ultra dynamic sky插件天气融合
晴天: 雨天: 雨天湿度: 小雪: 中雪: 找到该路径这个材质: 双击点开: 将Wet_Weather_Effects与Snow_Weather_Effects复制下来,包括参数节点 找到该路径这个材质,双击点开&…...
SpringCloud Gateway--Predicate/断言(详细介绍)下
😀前言 本篇博文是关于SpringCloud Gateway–Predicate/断言(详细介绍)下,希望你能够喜欢 🏠个人主页:晨犀主页 🧑个人简介:大家好,我是晨犀,希望我的文章可以…...
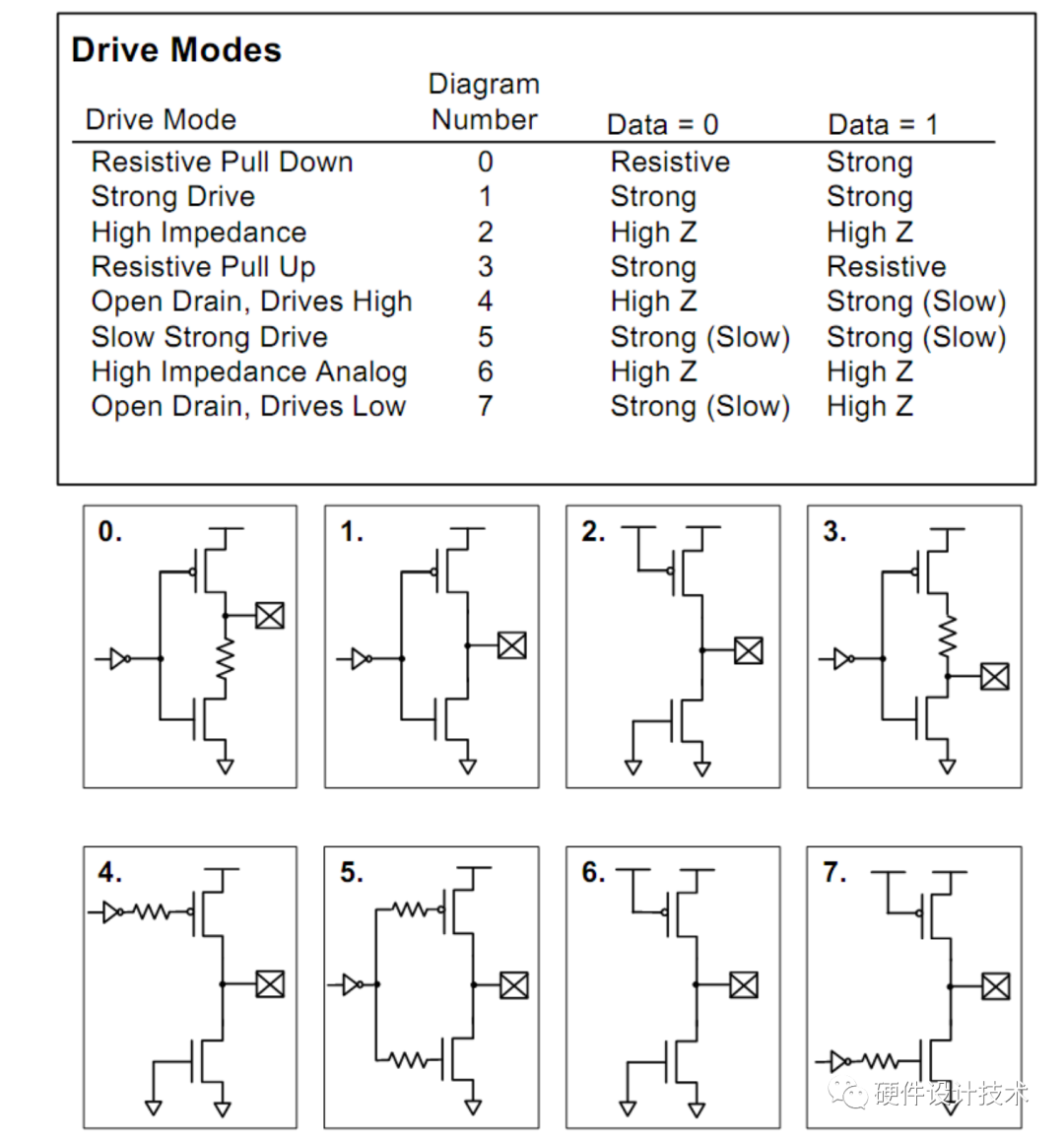
SOC芯片学习--GPIO简介
原创 硬件设计技术 硬件设计技术 2023-07-20 00:04 发表于广东 收录于合集#集成电路--IC7个 一、GPIO定义、分类: GPIO(英语:General-purpose input/output),通用型之输入输出的简称,其接脚可以供使用者由…...

skywalking源码本地编译运行经验总结
前言 最近工作原因在弄skywalking,为了进一步熟悉拉了代码下来准备debug,但是编译启动项目我就费了老大劲了,所以准备写这篇,帮兄弟们少踩点坑。 正确步骤 既然是用开源的东西,那么最好就是按照人家的方式使用&…...
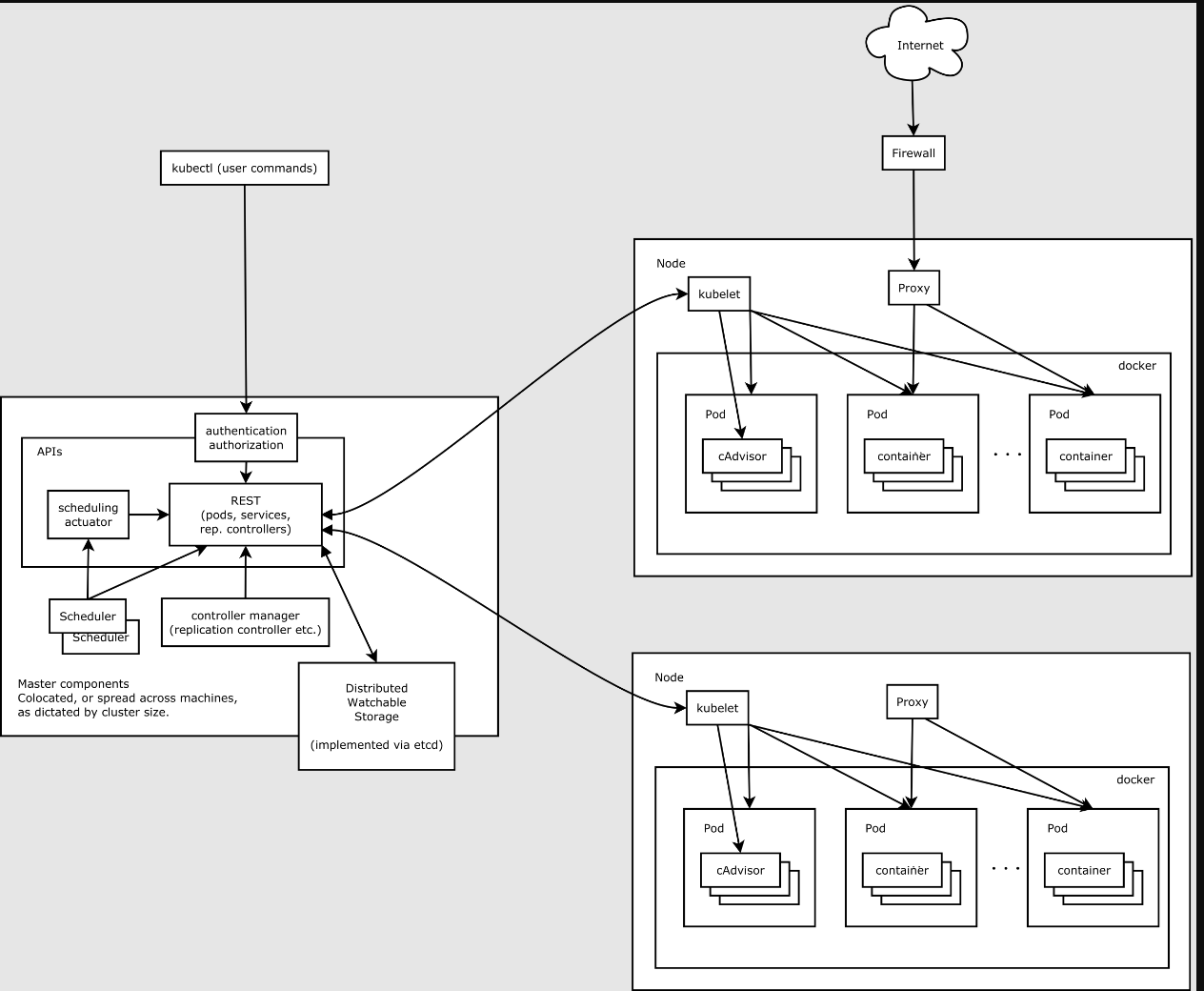
K8s架构简述
以部署一个nginx服务说明kubernetes系统各个组件调用关系: 一旦kubernetes环境启动之后,master和node都会将自身的信息存储到etcd数据库中 一个nginx服务的安装请求会首先被发送到master节点的apiServer组件 apiServer组件会调用scheduler组件来决定到底…...

linkedlist和arraylist的区别
LinkedList和ArrayList都是常见的数据结构,用于存储和操作集合元素,如果需要频繁进行插入和删除操作,LinkedList可能更适合。如果需要快速随机访问和较小的内存占用,ArrayList可能更合适。 以下是它们之间存在一些关键的区别&…...

[尚硅谷React笔记]——第2章 React面向组件编程
目录: 基本理解和使用: 使用React开发者工具调试函数式组件复习类的基本知识类式组件组件三大核心属性1: state 复习类中方法this指向: 复习bind函数:解决changeWeather中this指向问题:一般写法:state.htm…...

嵌入式学习笔记(40)看门狗定时器
7.5.1什么是看门狗、有何用 (1)看门狗定时器和普通定时器并无本质区别。定时器可以设定一个时间,在这个时间完成之前定时器不断计时,时间到的时候定时器会复位CPU(重启系统)。 (2)系统正常工作的时候当然不希望被重启࿰…...

点击、拖拉拽,BI系统让业务掌握数据分析主动权
在今天的商业环境中,数据分析已经成为企业获取竞争优势的关键因素之一。然而,许多企业在面对复杂的数据分析工具时,却常常感到困扰。这些工具往往需要专业的技术人员操作,而且界面复杂,难以理解和使用。对业务人员来说…...

C++模拟题[第一周-T1] 扑克
[第一周-T1] 扑克 题目描述 斗地主是一种使用 A \tt A A 到 K \tt K K 加上大小王的共 54 54 54 张扑克牌来进行的游戏,其中大小王各一张,其它数码牌各四张。在斗地主中,牌的大小关系根据牌的数码表示如下: 3 < 4 < 5 …...

ciscn_2019_s_9
ciscn_2019_s_9 Arch: i386-32-little RELRO: Partial RELRO Stack: No canary found NX: NX disabled PIE: No PIE (0x8048000) RWX: Has RWX segments32位,啥也没开,开心愉悦写shellcode int pwn() {char s[24]; // [esp8…...

微信、支付宝、百度、抖音开放平台第三方代小程序开发总结
大家好,我是小悟 小伙伴们都开启小长假了吧,值此中秋国庆双节之际,小悟祝所有的小伙伴们节日快乐。 支付宝社区很用心,还特意给寄了袋月饼,愿中秋节的圆月带给你身体健康,幸福团圆,国庆节的旗帜…...

C语言协程
协程(Coroutine)是一种程序运行方式,相比于线程和进程,协程更加轻量级,可以被视为一种用户态的线程,不需要内核的参与。 协程的特点在于其执行过程中可以被挂起(Suspend)࿰…...
)
RK3588安装python3.11(ubuntu18.04)
1.前言 看到rknn_toolkit_lite2更新了python3.11的安装包,马上更新一下 2.RK3588安装python3.11 Ubuntu上编译Python 3.11,您可以按照以下步骤进行操作: (1) 准备编译环境 在开始之前,确保您的系统已安装必要的编译工具和依赖项…...

‘Could not find first log file name in binary log index file‘的解决办法
mysql主从报异常Got fatal error 1236 from master when reading data from binary log: Could not find first log file name in binary log index file 数据库主从出错: Slave_IO_Running: No 一方面原因是因为网络通信的问题也有可能是日志读取错误的问题。以下是日志出错…...

快速排序与冒泡排序以及代码
快速排序 快速排序(Quicksort)是一种常用的排序算法,它基于分治的思想。 时间复杂度:O(nlogn) 空间复杂度:O(logn) 快速排序的基本思想如下: 选择一个元素…...
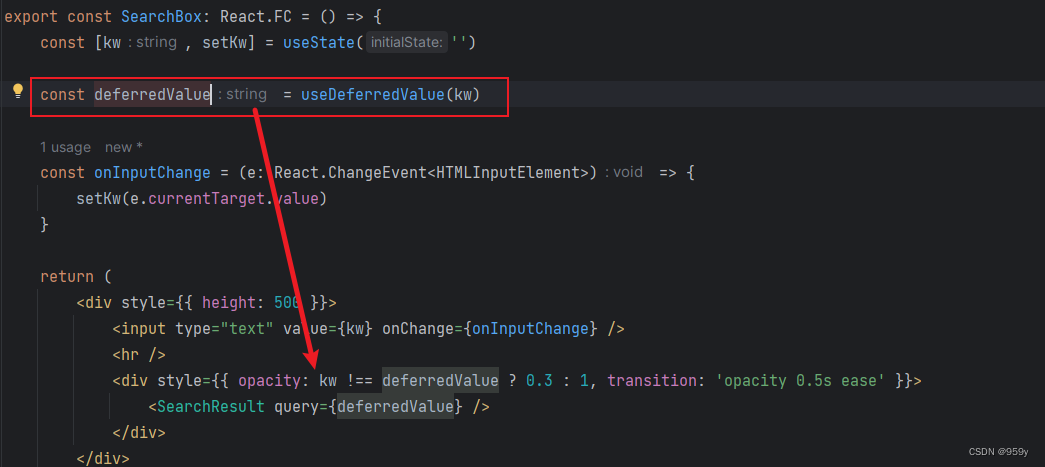
[React] 性能优化相关 (一)
文章目录 1.React.memo2.useMemo3.useCallback4.useTransition5.useDeferredValue 1.React.memo 当父组件被重新渲染的时候,也会触发子组件的重新渲染,这样就多出了无意义的性能开销。如果子组件的状态没有发生变化,则子组件是不需要被重新渲…...
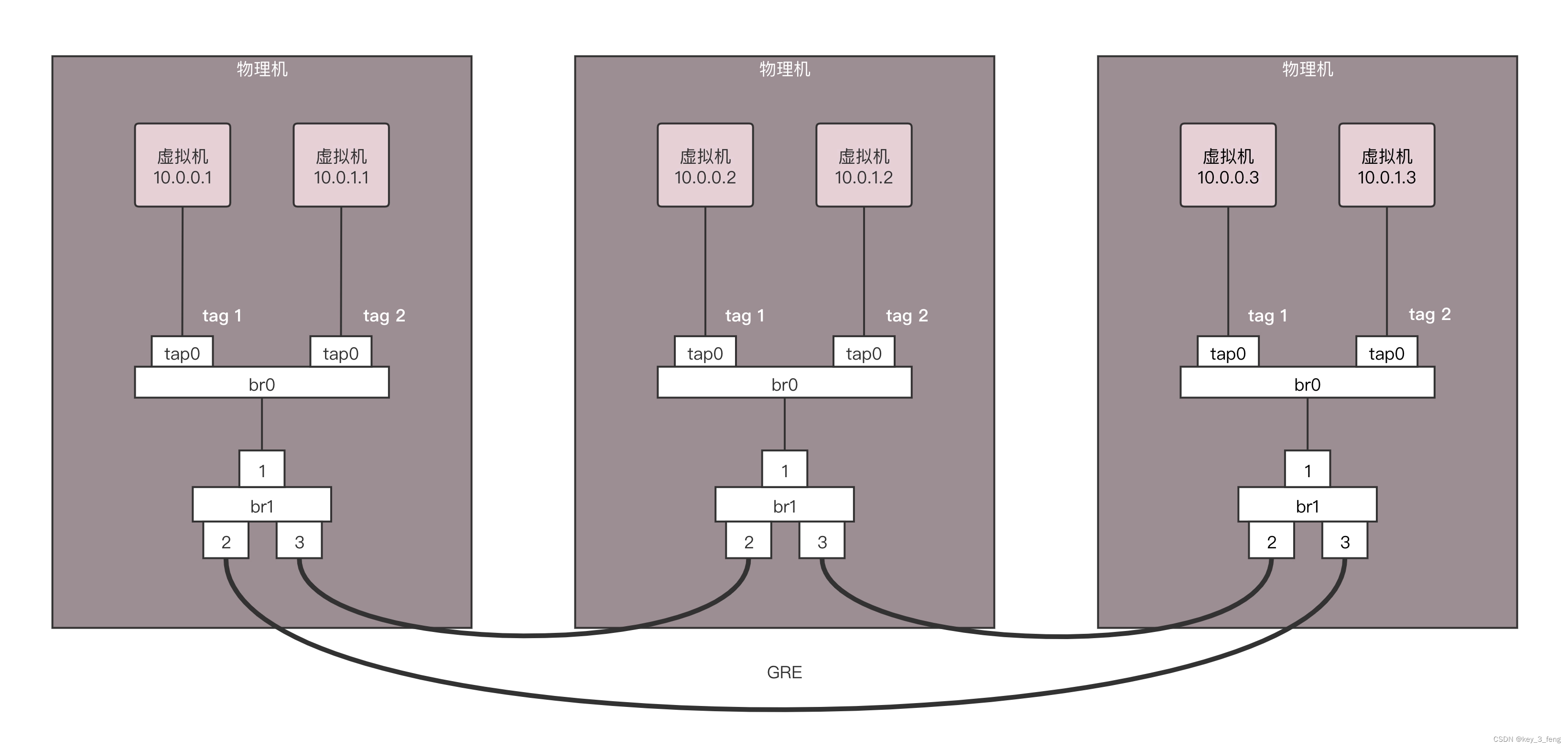
云中网络的隔离GREVXLAN
底层的物理网络设备组成的网络我们称为 Underlay 网络,而用于虚拟机和云中的这些技术组成的网络称为 Overlay 网络,这是一种基于物理网络的虚拟化网络实现。 第一个技术是 GRE,全称 Generic Routing Encapsulation,它是一种 IP-o…...

【【萌新的RiscV学习之流水线控制-9】】
萌新的RiscV学习之流水线控制-9 我们按照在之前的单周期设计加入控制单元 那么我们能够在后续的设计中提供方便 我们也在流水线中加入一个control单元 我们先按照书上的指令op码值介绍一遍基本功能 接下来我们讲述control 的 控制效果 关于这些串口判别的使用 由于控制线从…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

