云中网络的隔离GREVXLAN
底层的物理网络设备组成的网络我们称为 Underlay 网络,而用于虚拟机和云中的这些技术组成的网络称为 Overlay 网络,这是一种基于物理网络的虚拟化网络实现。
第一个技术是 GRE,全称 Generic Routing Encapsulation,它是一种 IP-over-IP 的隧道技术。它将 IP 包封装在 GRE 包里,外面加上 IP 头,在隧道的一端封装数据包,并在通路上进行传输,到另外一端的时候解封装。你可以认为 Tunnel 是一个虚拟的、点对点的连接。

使用 GRE 隧道,传输的过程就像下面这张图。这里面有两个网段、两个路由器,中间要通过 GRE 隧道进行通信。当隧道建立之后,会多出两个 Tunnel 端口,用于封包、解封包。
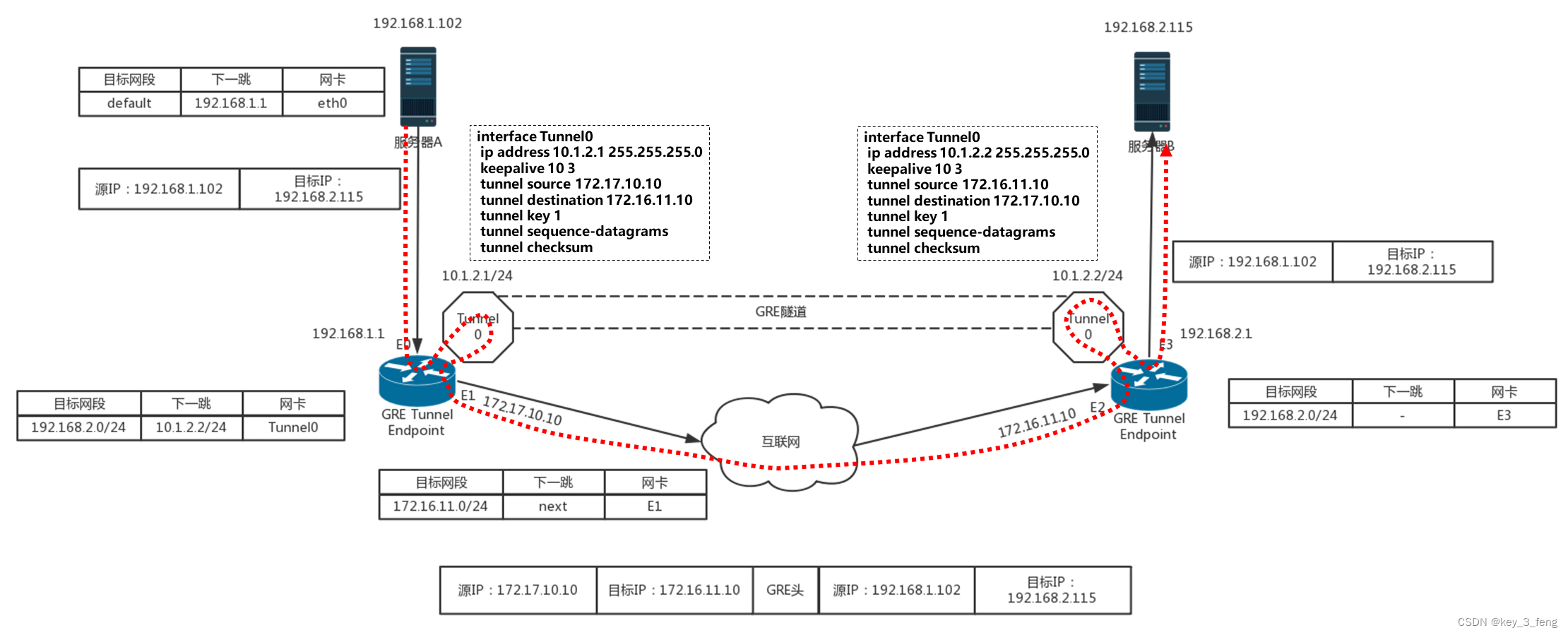
首先是 Tunnel 的数量问题。GRE 是一种点对点隧道,如果有三个网络,就需要在每两个网络之间建立一个隧道。如果网络数目增多,这样隧道的数目会呈指数性增长。

其次,GRE 不支持组播,因此一个网络中的一个虚机发出一个广播帧后,GRE 会将其广播到所有与该节点有隧道连接的节点。
另外一个问题是目前还是有很多防火墙和三层网络设备无法解析 GRE,因此它们无法对 GRE 封装包做合适地过滤和负载均衡。
第二种 Overlay 的技术称为 VXLAN。和三层外面再套三层的 GRE 不同,VXLAN 则是从二层外面就套了一个 VXLAN 的头,这里面包含的 VXLAN ID 为 24 位,也够用了。在 VXLAN 头外面还封装了 UDP、IP,以及外层的 MAC 头。
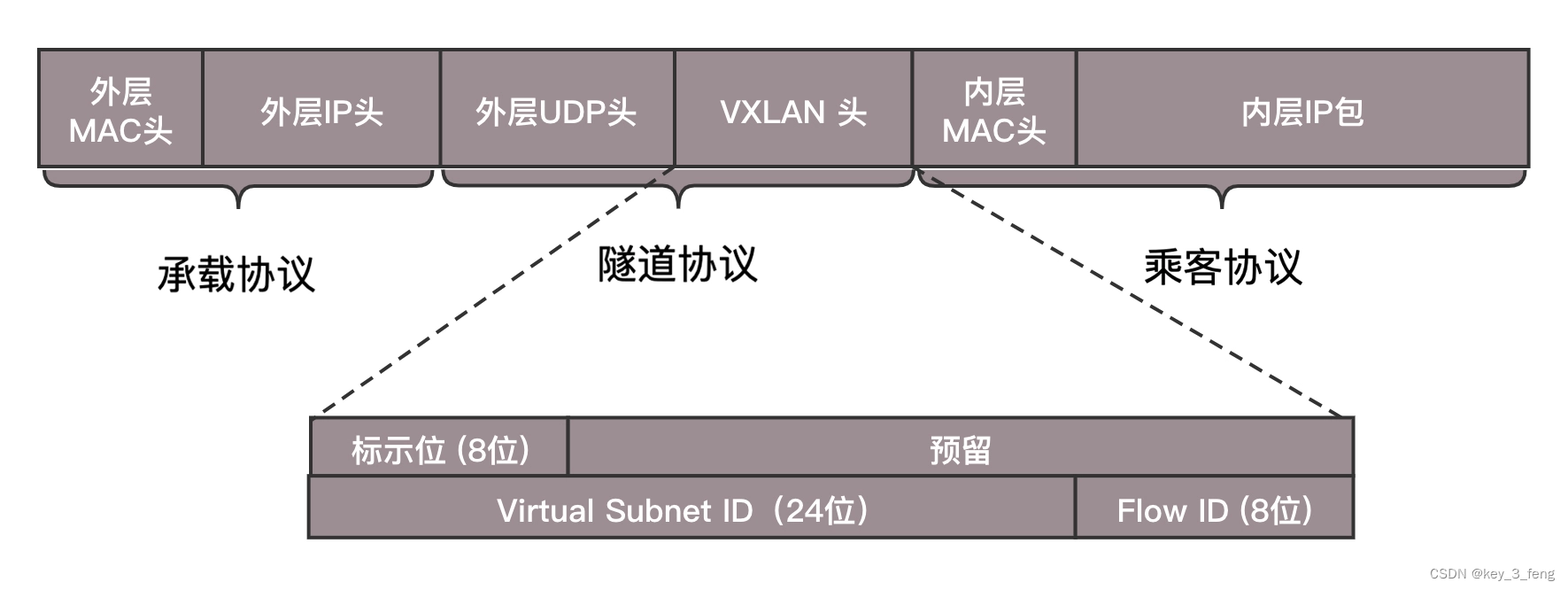
VXLAN 作为扩展性协议,也需要一个地方对 VXLAN 的包进行封装和解封装,实现这个功能的点称为 VTEP(VXLAN Tunnel Endpoint)。
VTEP 相当于虚拟机网络的管家。每台物理机上都可以有一个 VTEP。每个虚拟机启动的时候,都需要向这个 VTEP 管家注册,每个 VTEP 都知道自己上面注册了多少个虚拟机。当虚拟机要跨 VTEP 进行通信的时候,需要通过 VTEP 代理进行,由 VTEP 进行包的封装和解封装。
和 GRE 端到端的隧道不同,VXLAN 不是点对点的,而是支持通过组播的来定位目标机器的,而非一定是这一端发出,另一端接收。
当一个 VTEP 启动的时候,它们都需要通过 IGMP 协议。加入一个组播组,就像加入一个邮件列表,或者加入一个微信群一样,所有发到这个邮件列表里面的邮件,或者发送到微信群里面的消息,大家都能收到。而当每个物理机上的虚拟机启动之后,VTEP 就知道,有一个新的 VM 上线了,它归我管。

OpenvSwitch 支持三类隧道:GRE、VXLAN、IPsec_GRE。在使用 OpenvSwitch 的时候,虚拟交换机就相当于 GRE 和 VXLAN 封装的端点。
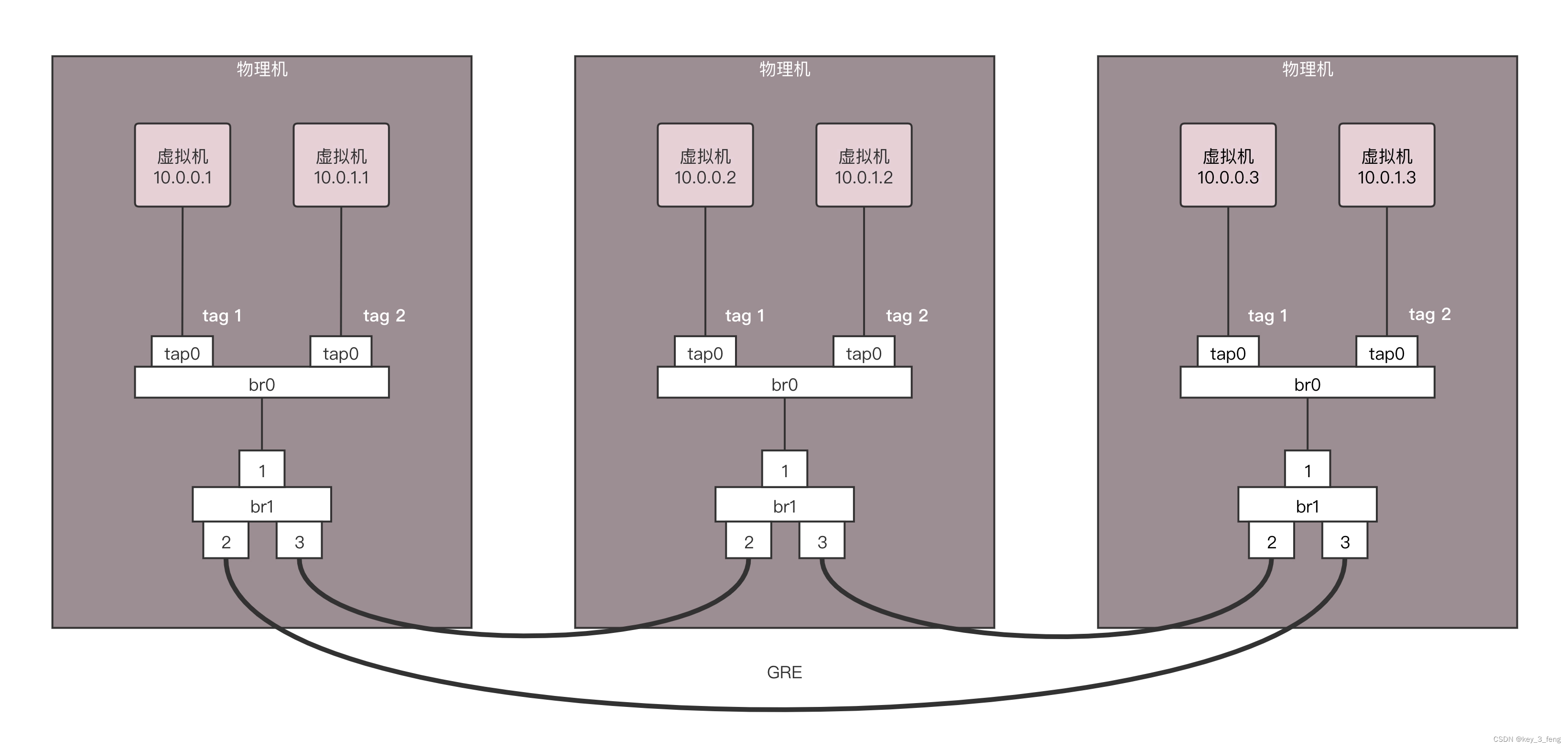
三台物理机,每台上都有两台虚拟机,分别属于两个不同的用户,因而 VLAN tag 都得打地不一样,这样才不能相互通信。但是不同物理机上的相同用户,是可以通过隧道相互通信的,因而通过 GRE 隧道可以连接到一起。
所有的 Flow Table 规则都设置在 br1 上,每个 br1 都有三个网卡,其中网卡 1 是对内的,网卡 2 和 3 是对外的。
此文章为9月Day28学习笔记,内容来源于极客时间《趣谈网络协议》,推荐该课程。
相关文章:

云中网络的隔离GREVXLAN
底层的物理网络设备组成的网络我们称为 Underlay 网络,而用于虚拟机和云中的这些技术组成的网络称为 Overlay 网络,这是一种基于物理网络的虚拟化网络实现。 第一个技术是 GRE,全称 Generic Routing Encapsulation,它是一种 IP-o…...

【【萌新的RiscV学习之流水线控制-9】】
萌新的RiscV学习之流水线控制-9 我们按照在之前的单周期设计加入控制单元 那么我们能够在后续的设计中提供方便 我们也在流水线中加入一个control单元 我们先按照书上的指令op码值介绍一遍基本功能 接下来我们讲述control 的 控制效果 关于这些串口判别的使用 由于控制线从…...

MySQL 通过存储过程高效插入100w条数据
目录 一、前言二、创建表三、编写存储过程插入数据四、高效插入数据方案4.1、插入数据时删除表中全部索引4.2、存储过程中使用统一事务插入(性能显著提升)4.3、调整MySQL系统配置(性能显著提升,适合存储过程没有使用统一事务&…...

国庆10.1
用select实现服务器并发 ser #include <myhead.h> #define ERR_MSG(msg) do{\fprintf(stderr, "__%d__", __LINE__);\perror(msg);\ }while(0)#define PORT 8888 //端口号,范围1024~49151 #define IP "192.168.1.205" //本机…...

[C++_containers]10分钟让你掌握vector
前言 在一个容器的创建或是使用之前,我们应该先明白这个容器的一些特征。 我们可以通过文档来来了解,当然我也会将重要的部分写在下面。 1. vector 是表示可变大小数组的序列容器。 2. 就像数组一样, vector 也采用的连续存储空间来存储元…...

前端与后端:程序中两个不同的领域
前端和后端是构成一个完整的计算机应用系统的两个主要部分。它们分别负责不同的功能和任务,有以下几个方面的区别: 功能:前端主要负责用户界面的呈现和交互,包括网页的设计、布局、样式、动画效果和用户输入等。后端则处理网站或应…...

vue3 +elementplus | vue2+elementui 动态地通过验证规则子新增或删除单个表单字段
效果图 点击 ‘’ 新增一行,点击‘-’ 删除一行 vue3elementplus写法 template <el-dialog v-model"dialogFormVisible" :title"title"><el-form ref"ruleFormRef" :model"form" :inline"true" lab…...

STM32之DMA
简介 • DMA ( Direct Memory Access )直接存储器存取 (可以直接访问STM32内部存储器,如SRAM、程序存储器Flash和寄存器等) •DMA可以提供外设和存储器或者存储器和存储器之间的高速数据传输,无须CPU干预&a…...
解决前端二进制流下载的文件(例如:excel)打不开的问题
1. 现在后端请求数据后,返回了一个二进制的数据,我们要把它下载下来。 这是响应的数据: 2. 这是调用接口的地方: uploadOk(){if(this.files.length 0){return this.$Message.warning("请选择上传文件!ÿ…...
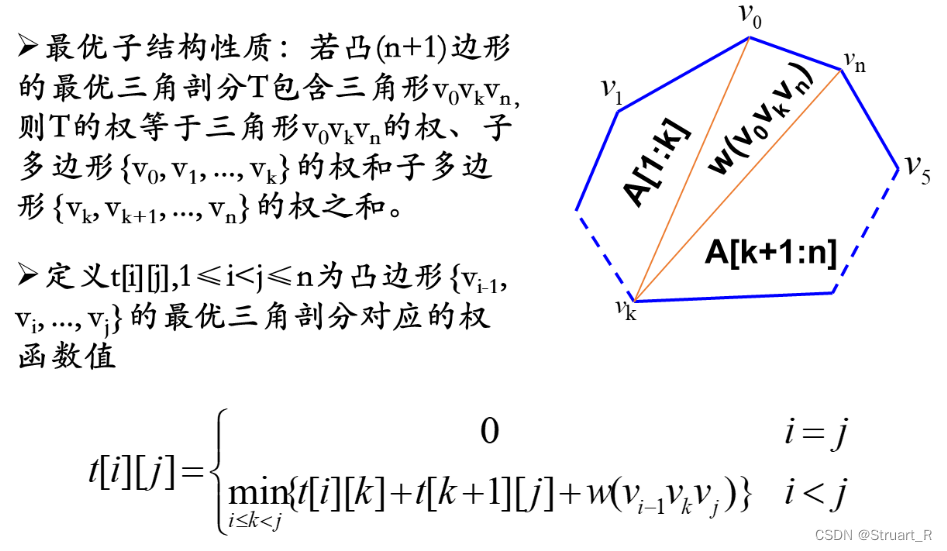
动态规划算法(1)--矩阵连乘和凸多边形剖分
目录 一、动态数组 1、创建动态数组 2、添加元素 3、删除修改元素 4、访问元素 5、返回数组长度 6、for each遍历数组 二、输入多个数字 1、正则表达式 2、has.next()方法 三、矩阵连乘 1、什么是矩阵连乘? 2、动态规划思路 3、手推m和s矩阵 4、完…...

通过Nginx重新认识HTTP错误码
文章目录 概要一、HTTP错误码1.1、1xx1.2、2xx1.3、3xx1.4、4xx1.5、5xx 二、Nginx对常见错误处理三、参考资料 概要 在web开发过程中,通过HTTP错误码快速定位问题是一个非常重要的技能,同时Nginx是非常常用的一个实现HTTP协议的服务,因此本…...

某房产网站登录RSA加密分析
文章目录 1. 写在前面2. 抓包分析3. 扣加密代码4. 还原加密 1. 写在前面 今天是国庆节,首先祝福看到这篇文章的每一个人节日快乐!假期会老的这些天一直在忙事情跟日常带娃,抽不出一点时间来写东西。夜深了、娃也睡了。最近湖南开始降温了&…...
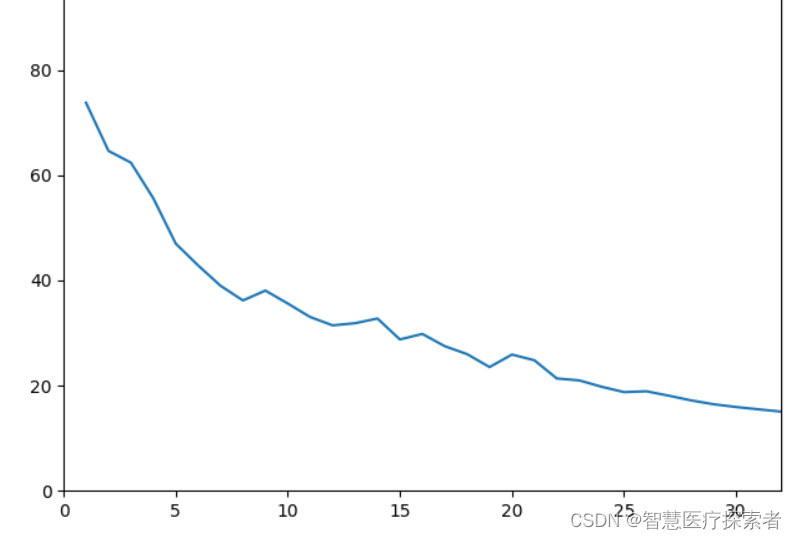
深度学习:基于长短时记忆网络LSTM实现情感分析
目录 1 LSTM网络介绍 1.1 LSTM概述 1.2 LSTM网络结构 1.3 LSTM门机制 1.4 双向LSTM 2 Pytorch LSTM输入输出 2.1 LSTM参数 2.2 LSTM输入 2.3 LSTM输出 2.4 隐藏层状态初始化 3 基于LSTM实现情感分析 3.1 情感分析介绍 3.2 数据集介绍 3.3 基于pytorch的代码实现 3…...
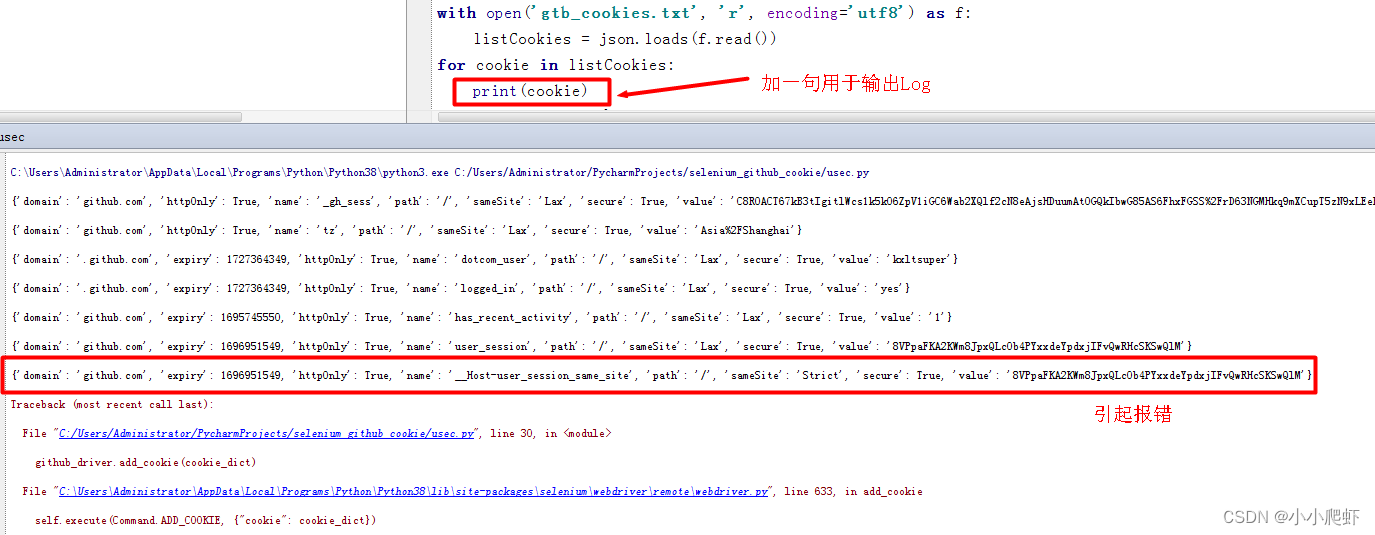
selenium使用已经获取的cookies登录网站报错unable to set cookie的处理方式
用selenium半手动登录github获取其登录cookies后,保存到一个文件gtb_cookies.txt中。 然后用selenium使用这个cookies文件,免登录上github。但是报错如下:selenium.common.exceptions.UnableToSetCookieException: Message: unable to set co…...
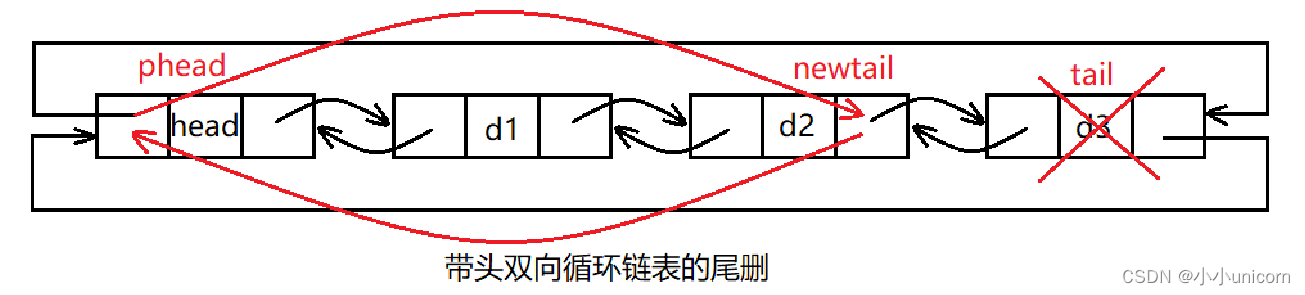
初阶数据结构(四)带头双向链表
💓博主csdn个人主页:小小unicorn ⏩专栏分类:数据结构 🚚代码仓库:小小unicorn的代码仓库🚚 🌹🌹🌹关注我带你学习编程知识 带头双向链表 链表的相关介绍初始化链表销毁链…...
2022年9月及10月
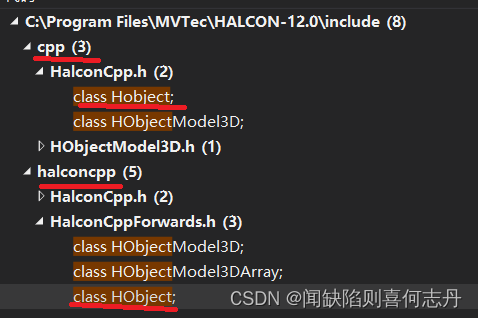
9月 1.Halcon12的HObject和Hobject halcon12 可以用HObject,也可以用Hobject,用法都一样 包括HalconCpp.h 如果附加目录中: C:\Program Files\MVTec\HALCON-12.0\include\halconcpp\ 在前面,则用 HalconCpp::HObject 如果附加目录…...

Vmware安装
title: “Vmware安装” createTime: 2021-11-22T09:53:2908:00 updateTime: 2021-11-22T09:53:2908:00 draft: false author: “name” tags: [“VMware”,“安装”,“linux”] categories: [“install”] description: “测试的” linux安装VMware Workstation16 1.安装包 …...

RSA算法
算法简介 RSA是一种非对称加密方式。发送者把明文通过公钥加密后发送出去,接受者把密文通过私钥解密得到明文。 算法过程 生成公钥和私钥 选取两个质数p和q,np*q。n的长度就是密钥长度。φ(n)(p-1)*(q-1)φ(n)为n的欧拉函数。找到1-φ(n)间与φ(n)互质的…...

计算机竞赛 深度学习手势识别 - yolo python opencv cnn 机器视觉
文章目录 0 前言1 课题背景2 卷积神经网络2.1卷积层2.2 池化层2.3 激活函数2.4 全连接层2.5 使用tensorflow中keras模块实现卷积神经网络 3 YOLOV53.1 网络架构图3.2 输入端3.3 基准网络3.4 Neck网络3.5 Head输出层 4 数据集准备4.1 数据标注简介4.2 数据保存 5 模型训练5.1 修…...

Spring的Ordered
Ordered Java中的Ordered接口是Spring框架中的一个接口,用于表示对象的顺序。它定义了一个方法getOrder(),用于获取对象的顺序值,值越小的对象越先被处理。 Ordered接口是Spring框架中的一个接口,用于定义组件的加载顺序。当一个…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
