SimpleCG动画示例--汉诺塔动画演示
前言
SimpleCG的使用方法在前面已经介绍了许多,有兴趣的同学如果有去动手,制作一些简单动画应该没多大问题的。所以这次我们来演示一下简单动画。我们刚学习C语言的递归函数时,有一个经典例子相信很多同学都写过,那就是汉诺塔。那么我们今天就来写一个汉诺塔的直观动画演示。
运行程序下载bin/AnimateHannuo.zip · master · b2b160 / SimpleCG_Demo · GitCode
一、全部源码
#include "../import/include/CGBoard.h"
#include "math.h"
#ifdef _DEBUG
#pragma comment(lib,"../import/lib/SimpleCG_MDd.lib")
#else
#pragma comment(lib,"../import/lib/SimpleCG_MT.lib")
#endif#define C_FLOOR_CNT 7
#define C_FLOOR_BOTTOM 380
#define C_HAN_HEIGHT 10
#define C_HAN_SPEED 30int g_nWidth = 640; //画面宽度
int g_nHeight= 400; //画面高度
enum ENUM_DIRECTION
{enumDIR_NULL,enumDIR_UP,enumDIR_DOWN
};
struct tagHannuo
{int nNumber;COLORREF nColor;int nWidth;int nPosHan;int nDir;POINT ptPos;
};tagHannuo g_pHannuo[C_FLOOR_CNT];
int g_nMoving = -1;
void DrawHan()
{int i;int j=0;setlinewidth(2);for(i=0;i<3; i++ ){_line( 100 + 200 * i, 50, 100 + 200 * i,C_FLOOR_BOTTOM );_line( 20 + 200 * i, C_FLOOR_BOTTOM, 180 + 200 * i,C_FLOOR_BOTTOM );}int nIndex = 0;for(j=0;j<3;++j){nIndex = 0;for(i=C_FLOOR_CNT-1;i>=0; i-- ){if(g_pHannuo[i].nPosHan == j && i != g_nMoving){setfillcolor(g_pHannuo[i].nColor);_solidrectangle( 100 +200 * g_pHannuo[i].nPosHan - g_pHannuo[i].nWidth/2, C_FLOOR_BOTTOM - nIndex * C_HAN_HEIGHT - C_HAN_HEIGHT, 100 +200 * g_pHannuo[i].nPosHan + g_pHannuo[i].nWidth/2, C_FLOOR_BOTTOM - nIndex * C_HAN_HEIGHT);++nIndex;}}}
}
void DrawMoving()
{if(g_nMoving>=0){setfillcolor(g_pHannuo[g_nMoving].nColor);_solidrectangle( g_pHannuo[g_nMoving].ptPos.x, g_pHannuo[g_nMoving].ptPos.y, g_pHannuo[g_nMoving].ptPos.x + g_pHannuo[g_nMoving].nWidth, g_pHannuo[g_nMoving].ptPos.y+ C_HAN_HEIGHT);}
}
void DrawAll()
{ClearDevice();DrawHan();DrawMoving();ReflushWindow();
}
void Moving( int nItem, int nFrom, int nTo )
{g_nMoving = nItem;g_pHannuo[nItem].ptPos.x = 100 +200 * nFrom - g_pHannuo[nItem].nWidth/2;for( g_pHannuo[nItem].ptPos.y = C_FLOOR_BOTTOM - C_FLOOR_CNT * C_HAN_HEIGHT; IsShowingWindow()&&g_pHannuo[nItem].ptPos.y>40; g_pHannuo[nItem].ptPos.y-=10 ){DrawAll();Sleep(C_HAN_SPEED);}int nXStep = (nTo - nFrom) * 5;int nDest = 100 +200 * nTo - g_pHannuo[nItem].nWidth/2;for( g_pHannuo[nItem].ptPos.x = 100 +200 * nFrom - g_pHannuo[nItem].nWidth/2; IsShowingWindow()&&abs(g_pHannuo[nItem].ptPos.x-nDest)>5; g_pHannuo[nItem].ptPos.x+=nXStep ){DrawAll();Sleep(C_HAN_SPEED);}g_pHannuo[nItem].ptPos.x = 100 +200 * nTo - g_pHannuo[nItem].nWidth/2;for( g_pHannuo[nItem].ptPos.y = 40; IsShowingWindow()&&g_pHannuo[nItem].ptPos.y<C_FLOOR_BOTTOM - C_FLOOR_CNT * C_HAN_HEIGHT; g_pHannuo[nItem].ptPos.y+=10 ){DrawAll();Sleep(C_HAN_SPEED);}g_nMoving = -1;g_pHannuo[nItem].nPosHan = nTo;
}
void MoveHan( int nFloor, int nFrom, int nTo, int nMiddle )
{if( nFloor == 1 ){Moving( nFloor-1, nFrom-1, nTo-1);return;}MoveHan( nFloor-1, nFrom, nMiddle, nTo );Moving( nFloor-1, nFrom-1, nTo-1);MoveHan( nFloor-1, nMiddle, nTo, nFrom );
}
void DrawProcess()
{bool bIsRunning = true;int i;srand(GetTickCount());for(i=0;i<C_FLOOR_CNT; i++ ){g_pHannuo[i].nNumber=i+1;g_pHannuo[i].nColor = RGB(rand()%200,rand()%200,rand()%200);g_pHannuo[i].nDir = enumDIR_NULL;g_pHannuo[i].nPosHan = 0;g_pHannuo[i].nWidth = 20*(i+1);}MoveHan(C_FLOOR_CNT,1,2,3);DrawAll();
}
int _tmain(int argc, _TCHAR* argv[])
{//初始化if( !ShowingBoard(g_nWidth,g_nHeight, DrawProcess))return 1;//关闭图库CloseBoard();return 0;
}
对于写过汉诺塔的同学来说,程序逻辑应该没什么难度,就是在递归程序上增加了动画过程。
二、演示效果
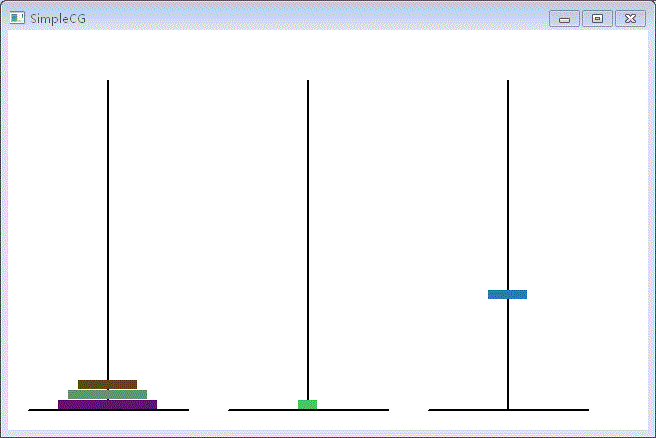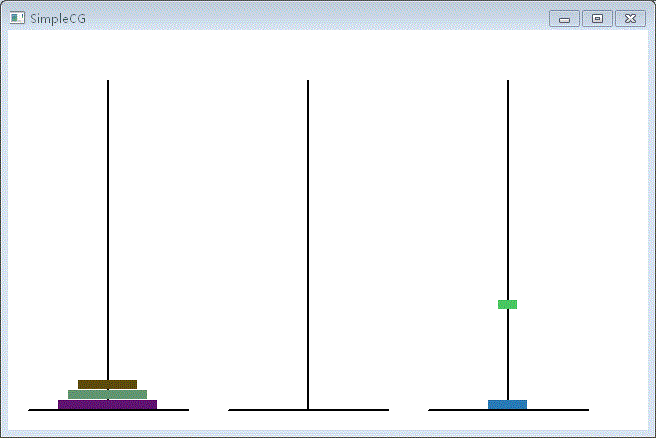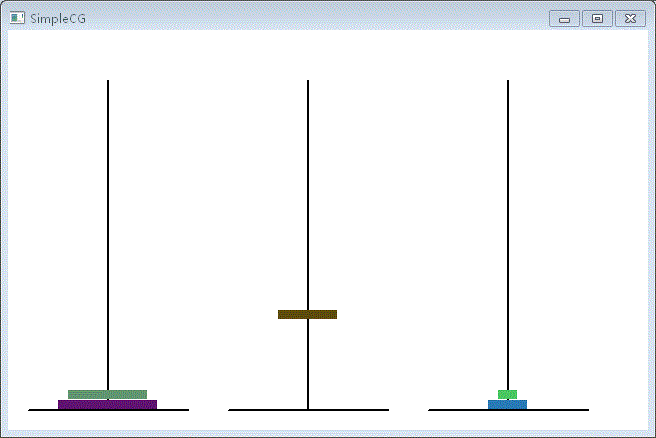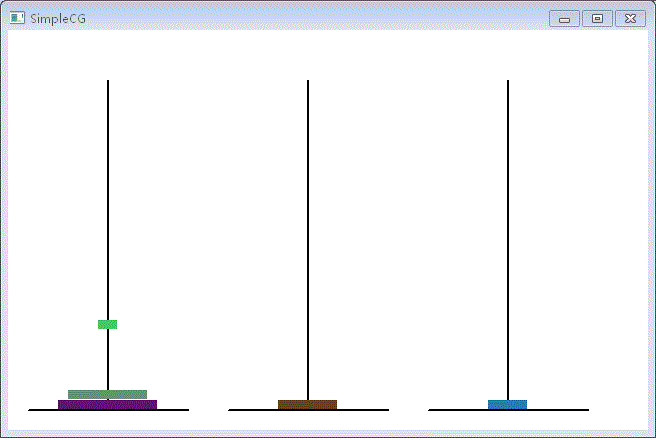
对于5层来说是不难的,但递归对于层数增加所带来的时间消耗是呈指数增加的,所以通过动画来观察层数增加带来的时间消耗非常直观。在原始的汉诺塔里是64层,要移完所有的层数将会世界末日,因为即便到世界的尽头也无法完成。有兴趣的同学可以把代码输入并把层数加大看看。
三、代码下载
汉诺塔演示源代码
AnimateHannuo · master · b2b160 / SimpleCG_Demo · GitCode
库安装方法如下
SimpleCG库安装使用_b2b160的博客-CSDN博客
相关文章:

SimpleCG动画示例--汉诺塔动画演示
前言 SimpleCG的使用方法在前面已经介绍了许多,有兴趣的同学如果有去动手,制作一些简单动画应该没多大问题的。所以这次我们来演示一下简单动画。我们刚学习C语言的递归函数时,有一个经典例子相信很多同学都写过,那就是汉诺塔。那…...
)
反弹shell脚本(php-reverse-shell)
平时经常打靶机 这里贴一个 反弹shell的脚本 <?php // php-reverse-shell - A Reverse Shell implementation in PHP // Copyright (C) 2007 pentestmonkeypentestmonkey.net // // This tool may be used for legal purposes only. Users take full responsibility // f…...

XSS-labs
XSS常见的触发标签_xss标签_H3rmesk1t的博客-CSDN博客 该补习补习xss漏洞了 漏洞原理 网站存在 静态 和 动态 网站 xss 针对的网站 就是 动态网站 动态网站会根据 用户的环境 与 需求 反馈出 不同的响应静态页面 代码写死了 只会存在代码中有的内容 通过动态网站 用户体…...

C++简单实现AVL树
目录 一、AVL树的概念 二、AVL树的性质 三、AVL树节点的定义 四、AVL树的插入 4.1 parent的平衡因子为0 4.2 parent的平衡因子为1或-1 4.3 parent的平衡因子为2或-2 4.3.1 左单旋 4.3.2 右单旋 4.3.3 先左单旋再右单旋 4.3.4 先右单旋再左单旋 4.4 插入节点完整代码…...
UE4 Cesium 与ultra dynamic sky插件天气融合
晴天: 雨天: 雨天湿度: 小雪: 中雪: 找到该路径这个材质: 双击点开: 将Wet_Weather_Effects与Snow_Weather_Effects复制下来,包括参数节点 找到该路径这个材质,双击点开&…...
SpringCloud Gateway--Predicate/断言(详细介绍)下
😀前言 本篇博文是关于SpringCloud Gateway–Predicate/断言(详细介绍)下,希望你能够喜欢 🏠个人主页:晨犀主页 🧑个人简介:大家好,我是晨犀,希望我的文章可以…...
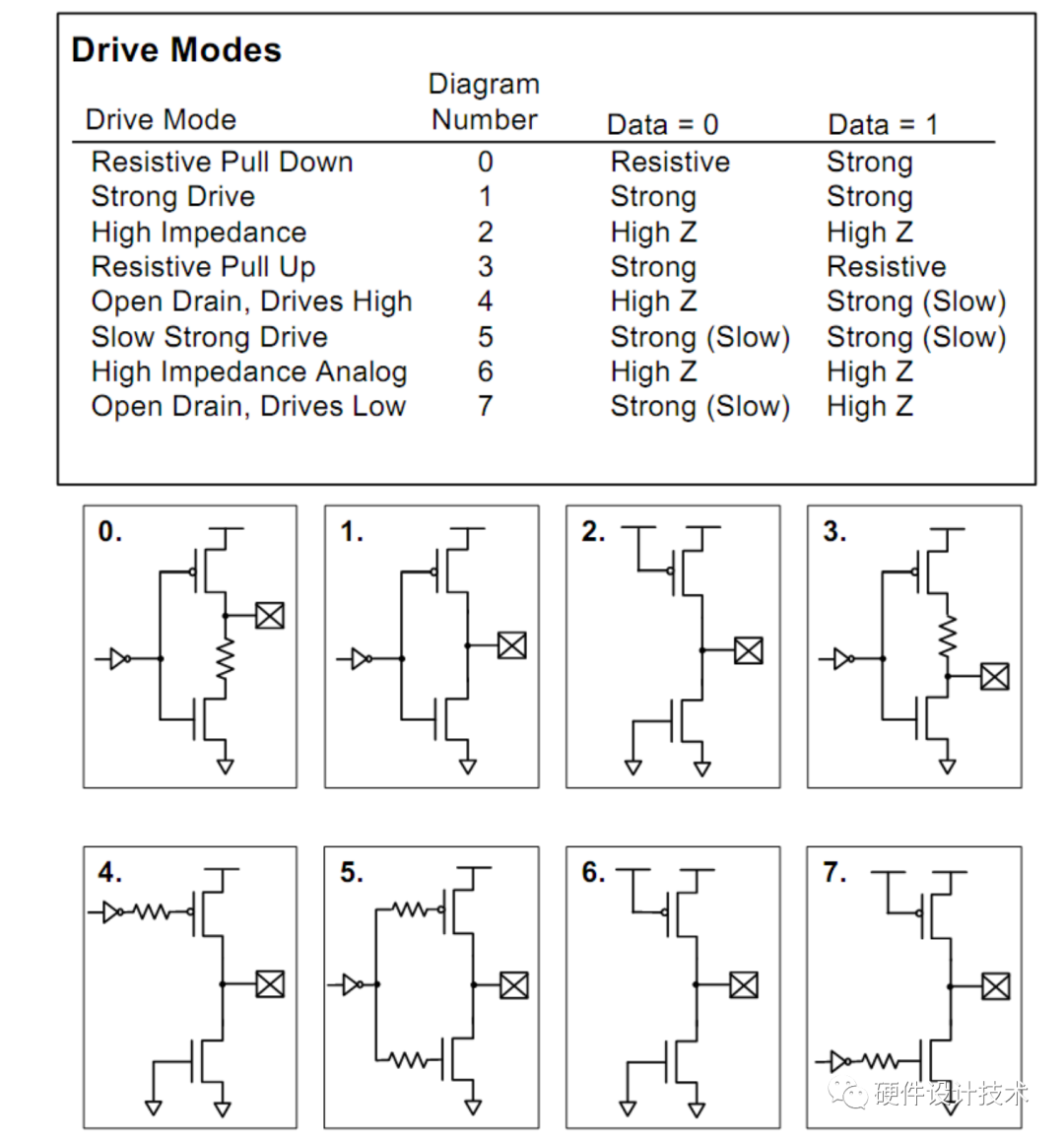
SOC芯片学习--GPIO简介
原创 硬件设计技术 硬件设计技术 2023-07-20 00:04 发表于广东 收录于合集#集成电路--IC7个 一、GPIO定义、分类: GPIO(英语:General-purpose input/output),通用型之输入输出的简称,其接脚可以供使用者由…...

skywalking源码本地编译运行经验总结
前言 最近工作原因在弄skywalking,为了进一步熟悉拉了代码下来准备debug,但是编译启动项目我就费了老大劲了,所以准备写这篇,帮兄弟们少踩点坑。 正确步骤 既然是用开源的东西,那么最好就是按照人家的方式使用&…...
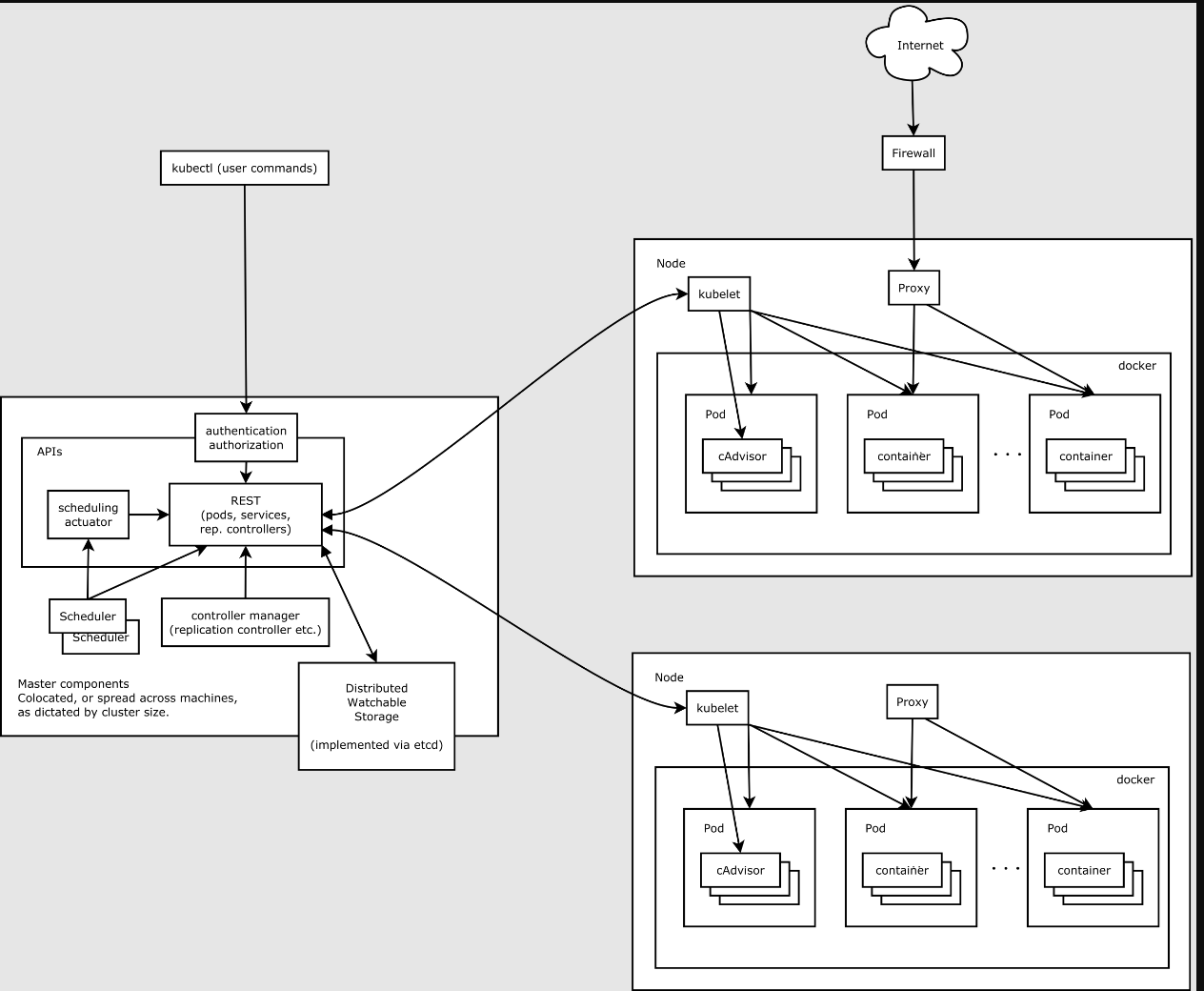
K8s架构简述
以部署一个nginx服务说明kubernetes系统各个组件调用关系: 一旦kubernetes环境启动之后,master和node都会将自身的信息存储到etcd数据库中 一个nginx服务的安装请求会首先被发送到master节点的apiServer组件 apiServer组件会调用scheduler组件来决定到底…...

linkedlist和arraylist的区别
LinkedList和ArrayList都是常见的数据结构,用于存储和操作集合元素,如果需要频繁进行插入和删除操作,LinkedList可能更适合。如果需要快速随机访问和较小的内存占用,ArrayList可能更合适。 以下是它们之间存在一些关键的区别&…...

[尚硅谷React笔记]——第2章 React面向组件编程
目录: 基本理解和使用: 使用React开发者工具调试函数式组件复习类的基本知识类式组件组件三大核心属性1: state 复习类中方法this指向: 复习bind函数:解决changeWeather中this指向问题:一般写法:state.htm…...

嵌入式学习笔记(40)看门狗定时器
7.5.1什么是看门狗、有何用 (1)看门狗定时器和普通定时器并无本质区别。定时器可以设定一个时间,在这个时间完成之前定时器不断计时,时间到的时候定时器会复位CPU(重启系统)。 (2)系统正常工作的时候当然不希望被重启࿰…...

点击、拖拉拽,BI系统让业务掌握数据分析主动权
在今天的商业环境中,数据分析已经成为企业获取竞争优势的关键因素之一。然而,许多企业在面对复杂的数据分析工具时,却常常感到困扰。这些工具往往需要专业的技术人员操作,而且界面复杂,难以理解和使用。对业务人员来说…...

C++模拟题[第一周-T1] 扑克
[第一周-T1] 扑克 题目描述 斗地主是一种使用 A \tt A A 到 K \tt K K 加上大小王的共 54 54 54 张扑克牌来进行的游戏,其中大小王各一张,其它数码牌各四张。在斗地主中,牌的大小关系根据牌的数码表示如下: 3 < 4 < 5 …...

ciscn_2019_s_9
ciscn_2019_s_9 Arch: i386-32-little RELRO: Partial RELRO Stack: No canary found NX: NX disabled PIE: No PIE (0x8048000) RWX: Has RWX segments32位,啥也没开,开心愉悦写shellcode int pwn() {char s[24]; // [esp8…...

微信、支付宝、百度、抖音开放平台第三方代小程序开发总结
大家好,我是小悟 小伙伴们都开启小长假了吧,值此中秋国庆双节之际,小悟祝所有的小伙伴们节日快乐。 支付宝社区很用心,还特意给寄了袋月饼,愿中秋节的圆月带给你身体健康,幸福团圆,国庆节的旗帜…...

C语言协程
协程(Coroutine)是一种程序运行方式,相比于线程和进程,协程更加轻量级,可以被视为一种用户态的线程,不需要内核的参与。 协程的特点在于其执行过程中可以被挂起(Suspend)࿰…...
)
RK3588安装python3.11(ubuntu18.04)
1.前言 看到rknn_toolkit_lite2更新了python3.11的安装包,马上更新一下 2.RK3588安装python3.11 Ubuntu上编译Python 3.11,您可以按照以下步骤进行操作: (1) 准备编译环境 在开始之前,确保您的系统已安装必要的编译工具和依赖项…...

‘Could not find first log file name in binary log index file‘的解决办法
mysql主从报异常Got fatal error 1236 from master when reading data from binary log: Could not find first log file name in binary log index file 数据库主从出错: Slave_IO_Running: No 一方面原因是因为网络通信的问题也有可能是日志读取错误的问题。以下是日志出错…...

快速排序与冒泡排序以及代码
快速排序 快速排序(Quicksort)是一种常用的排序算法,它基于分治的思想。 时间复杂度:O(nlogn) 空间复杂度:O(logn) 快速排序的基本思想如下: 选择一个元素…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...
