数据结构与算法之最小爬楼梯费用动态规划
继续上一道题目,在上一道题目的基础之上,我们来解决这一道爬楼梯最小费用题。
一.题目描述


二.思路(动态规划五部曲)
确定dp数组以及下标的含义
使用动态规划,就要有一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了。
dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
对于dp数组的定义,大家一定要清晰!
2.确定递推公式
可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?
一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
3.dp数组如何初始化
看一下递归公式,dp[i]由dp[i - 1],dp[i - 2]推出,既然初始化所有的dp[i]是不可能的,那么只初始化dp[0]和dp[1]就够了,其他的最终都是dp[0]dp[1]推出。
那么 dp[0] 应该是多少呢? 根据dp数组的定义,到达第0台阶所花费的最小体力为dp[0],那么有同学可能想,那dp[0] 应该是 cost[0],例如 cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 的话,dp[0] 就是 cost[0] 应该是1。
4.确定遍历顺序
最后一步,递归公式有了,初始化有了,如何遍历呢?
因为是模拟台阶,而且dp[i]由dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了。
5.举例推导dp数组
拿示例2:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟一下dp数组的状态变化,如下:
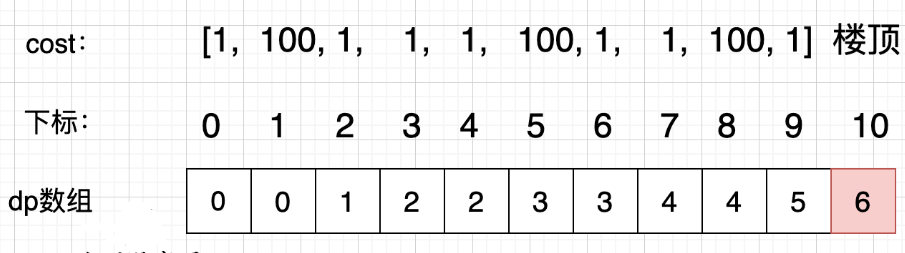
如果大家代码写出来有问题,就把dp数组打印出来,看看和如上推导的是不是一样的。
以上分析完毕,整体C++代码如下:
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {vector<int> dp(cost.size() + 1);dp[0] = 0; // 默认第一步都是不花费体力的dp[1] = 0;for (int i = 2; i <= cost.size(); i++) {dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}return dp[cost.size()];}
};时间复杂度:O(n)
空间复杂度:O(n)
大家可以发现这道题目相对于上一道题目又难了一点,但整体思路是一样的。
大家加油!
相关文章:

数据结构与算法之最小爬楼梯费用动态规划
继续上一道题目,在上一道题目的基础之上,我们来解决这一道爬楼梯最小费用题。一.题目描述二.思路(动态规划五部曲)确定dp数组以及下标的含义使用动态规划,就要有一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了。dp[i]的…...

阿里云ACA认证如何获取?
获取阿里云ACA(Alibaba Cloud Certification Associate)认证,需要按照以下步骤进行操作: 注册阿里云账号。如果您还没有阿里云账号,请先注册一个账号。登录阿里云官网。登录后,进入阿里云认证中心。选择AC…...
【Python入门第十六天】Python If ... Else
Python 条件和 If 语句 Python 支持来自数学的常用逻辑条件: 等于:a b不等于:a ! b小于:a < b小于等于:a < b大于:a > b大于等于:a > b 这些条件能够以多种方式使用,…...

两数之和的解法
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。你可以按任意顺序返回答案…...
领导催我优化SQL语句,我求助了ChatGPT。这是ChatGPT给出的建议,你们觉得靠谱吗
作为一个程序员,无论在面试还是工作中,优化SQL都是绕不过去的难题。 为啥?工作之后才会明白,随着公司的业务量增多,SQL的执行效率对程系统运行效率的影响逐渐增大,相对于改造代码,优化SQL语句是…...
ArcGIS手动分割矢量面要素从而划分为多个面部分的方式:Cut Polygons Tool
本文介绍在ArcGIS下属ArcMap软件中,通过“Cut Polygons Tool”工具,对一个面要素矢量图层加以手动分割,从而将其划分为指定形状的多个部分的方法。 对于一个面要素矢量文件,有时我们需要对其加以划分,通过手动勾勒新的…...

【LeetCode】剑指 Offer 13. 机器人的运动范围 p92 -- Java Version
题目链接:https://leetcode.cn/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/ 1. 题目介绍(13. 机器人的运动范围) 地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动࿰…...

[oeasy]python0091_仙童公司_八叛逆_intel_8080_altair8800_牛郎星
编码进化 个人电脑 计算机 通过电话网络 进行连接 极客 利用技术 做一些有趣的尝试 极客文化 是 认真研究技术的 文化 计算机 不再是 高校和研究机构高墙里面的 神秘事物而是 生活中常见的 家用电器 ibm 蓝色巨人脚步沉重 dec 小型机不断蚕食低端市场甚至组成网络干掉大型机…...

crontab 执行脚本报错,手动执行脚本正常的解决方法
一、出现的问题 有一个守护脚本XXX.sh,需要使用oracle用户在linux上配置定时任务,每1分钟检查执行一次。但是发现该脚本使用oralce用户手动启动没问题,能正常把程序启动起来,而使用crontab并没有把程序启动起来。 二、排查分析问…...

扎心话题 | 设计院背后的潜规则你知道吗?
大家好,我是建模助手。 大家都知道,在过去的2022年经济是真难!以小编所在的广东为例,全年GDP增长仅1.9%。 这个数据足以呈现一个社会现象——不仅消费力咔咔下降,各行各业更有不同程度地嗝屁。这其中也包括一些设计院…...

【JavaEE初阶】第二节.多线程( 进阶篇 ) 锁的优化、JUC的常用类、线程安全的集合类
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、synchronized的优化操作 1.1 锁膨胀/锁升级 1.2 锁消除 1.3 锁粗化二、JUC 2.1 Callable接口 2.2 ReentrantLock类&…...

大数据核心技术是什么
大数据的核心层:数据采集层、数据存储与分析层、数据共享层、数据应用层,可能叫法有所不同本质上的角色都大同小异。 大数据的核心技术都包括什么? 1、数据采集 数据采集的任务就是把数据从各种数据源中采集和存储到数据存储上,…...

「TCG 规范解读」初识 TPM 2.0 库续一
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...

task与function
task和function主要是有助于代码的可重用性,都可以在module-endmodule之外声明。 1.function 1.1.function逻辑的综合 function:一个只有1个wire型输出值、全是组合逻辑的函数,且函数名即输出信号名,小括号中按顺序例化输入信号。…...
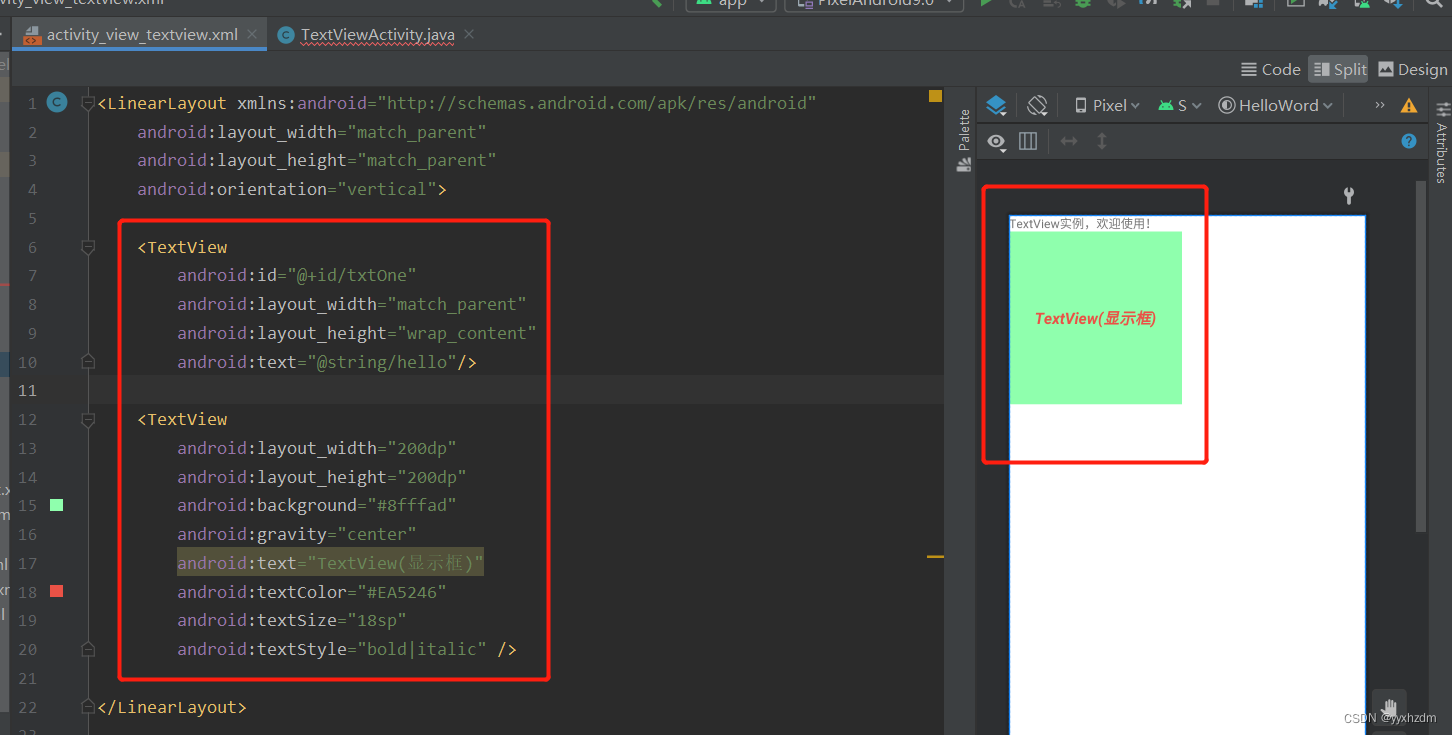
Android 基础知识4-3.1 TextView(文本框)详解
一、前言 TextView就是一个显示文本标签的控件,就是用来显示文本。可以在代码或者 XML中设置字体,字体大小,字体颜色 ,字体样式 (加粗级斜体),文字截断(比如:只显示10个字…...
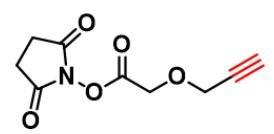
点击化学 PEG 试剂1858242-47-3,Propargyl丙炔基-PEG1-乙酸活性酯
Propargyl-PEG1-Acetic acid-NHS ester,丙炔基-聚乙二醇-乙酸琥珀酰亚胺酯,丙炔基-PEG1-乙酸活性酯,丙炔基-PEG1-乙酸-NHS 酯产品规格:1.CAS号:1858242-47-32.分子式:C9H9NO53.分子量:211.174.包…...

正则表达式是如何运作的?
在日常的开发工作当中,我们必不可免的会碰到需要使用正则的情况。 正则在很多时候通过不同的组合方式最后都可以达到既定的目标结果。比如我们有一个需要匹配的字符串: hello,我们可以通过 / .</p>/ 以及 / .?</p>/ 来匹配&…...

JVM参数GC线程数ParallelGCThreads设置
1. ParallelGCThreads参数含义JVM垃圾回收(GC)算法的两个优化标的:吞吐量和停顿时长。JVM会使用特定的GC收集线程,当GC开始的时候,GC线程会和业务线程抢占CPU时间,吞吐量定义为CPU用于业务线程的时间与CPU总消耗时间的比值。为了承…...

java 线程的那些事
什么是进程: 你把它理解成一个软件 什么是线程: 你把它理解成软件里面的一个功能,做的事情 什么是多线程: 你把它理解成 软件里面的某一个功能,原先是一个人累死累活的在那里完成,现在好了,多…...
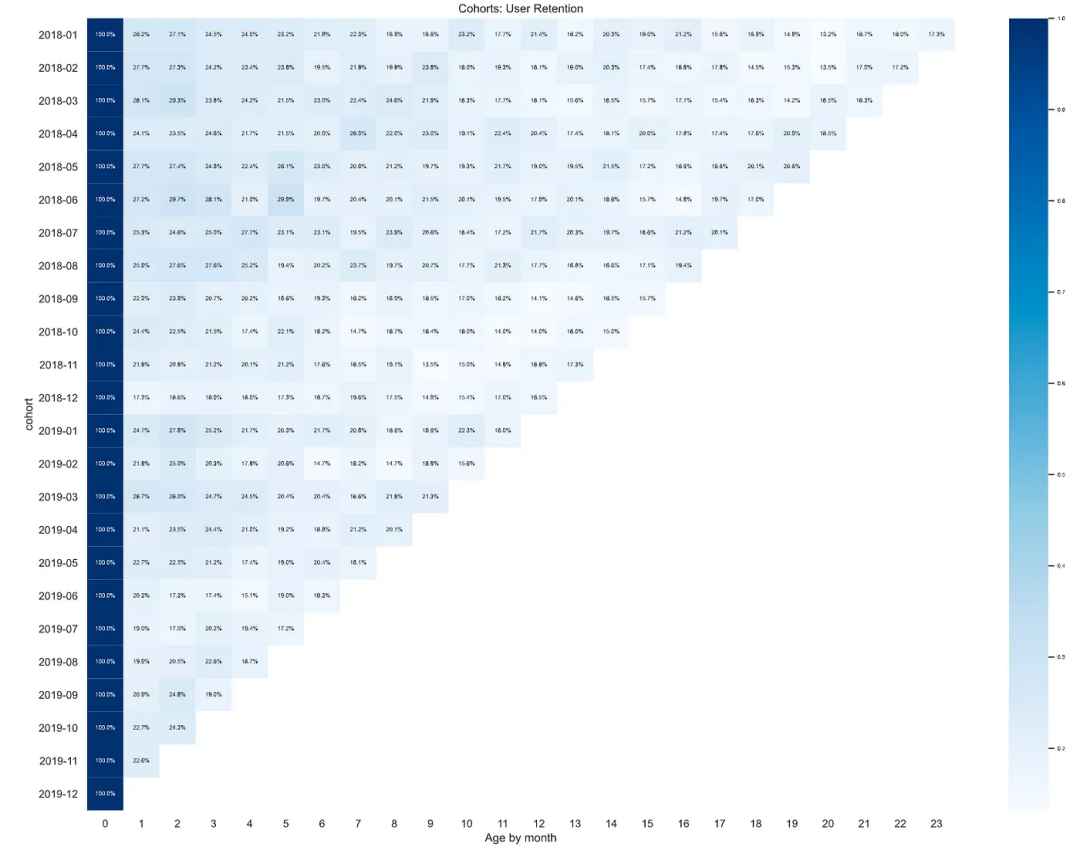
如何利用 Python 进行客户分群分析(附源码)
每个电子商务数据分析师必须掌握的一项数据聚类技能 如果你是一名在电子商务公司工作的数据分析师,从客户数据中挖掘潜在价值,来提高客户留存率很可能就是你的工作任务之一。 然而,客户数据是巨大的,每个客户的行为都不一样。20…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
