【LeetCode】剑指 Offer 13. 机器人的运动范围 p92 -- Java Version
题目链接:https://leetcode.cn/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/
1. 题目介绍(13. 机器人的运动范围)
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
【测试用例】:
示例 1:
输入:m = 2, n = 3, k = 1
输出:3
示例 2:
输入:m = 3, n = 1, k = 0
输出:1
【条件约束】:
提示:
- 1 <= n,m <= 100
- 0 <= k <= 20
2. 题解
2.1 回溯(DFS+剪枝)-- O(mn)
时间复杂度O(mn),空间复杂度O(mn)
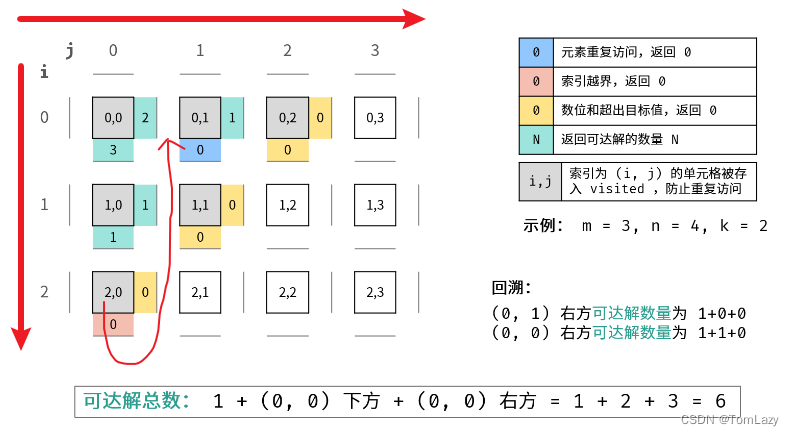
- 深度优先搜索: 可以理解为暴力法模拟机器人在矩阵中的所有路径。DFS 通过递归,先朝一个方向搜到底,再回溯至上个节点,沿另一个方向搜索,以此类推,过程如上图所示。
- 剪枝: 在搜索中,遇到数位和超出目标值、此元素已访问,则应立即返回,称之为 可行性剪枝 。
class Solution {// 1. 从[0,0]位置起始出发// 2. 向方格四面八方判断// 3. 统计机器人可到达的格子总数public int movingCount(int m, int n, int k) {// 错误判断if (m <= 0 || n <= 0 || k < 0) return 0;// 辅助数组:用来标记当前格子是否被访问过boolean[][] visited = new boolean[m][n];// 从(0,0)开始出发return dfs(0,0,m,n,k,visited);}public int dfs(int i, int j, int m, int n, int k, boolean[][] visited) {// 递归终止条件:错误判断if(i >= m || j >= n || k <getDigitSum(i) + getDigitSum(j) || visited[i][j]) return 0;// 该位置通过了错误判断,说明该方格属于机器人可达visited[i][j] = true;// 当前格 + 往下走 + 往右走,因为是0出发,不是从任意点出发,所以这里就不需要从四个方向都进行相加return 1 + dfs(i + 1, j, m, n, k, visited) + dfs(i, j + 1, m, n, k, visited);}// 求一个非负整数的数位之和public int getDigitSum(int number){int sum = 0;while (number > 0){sum += number % 10;number = number/10;}return sum;}}
2.2 BFS – O(mn)
时间复杂度O(mn),空间复杂度O(mn)

class Solution {public int movingCount(int m, int n, int k) {boolean[][] visited = new boolean[m][n];int res = 0;Queue<int[]> queue= new LinkedList<int[]>();queue.add(new int[] { 0, 0, 0, 0 });while(queue.size() > 0) {int[] x = queue.poll();int i = x[0], j = x[1], si = x[2], sj = x[3];if(i >= m || j >= n || k < si + sj || visited[i][j]) continue;visited[i][j] = true;res ++;queue.add(new int[] { i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj });queue.add(new int[] { i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8 });}return res;}
}3. 参考资料
[1] 剑指 Offer 13. 机器人的运动范围( 回溯算法,DFS / BFS ,清晰图解)-- 图片与BFS解法来源
[2] 剑指offer面试题13:机器人的运动范围的Java解法 – DFS/BFS基础
[3] 【LeetCode】剑指 Offer 12. 矩阵中的路径 p89 – Java Version – 相似题目
相关文章:

【LeetCode】剑指 Offer 13. 机器人的运动范围 p92 -- Java Version
题目链接:https://leetcode.cn/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/ 1. 题目介绍(13. 机器人的运动范围) 地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动࿰…...

[oeasy]python0091_仙童公司_八叛逆_intel_8080_altair8800_牛郎星
编码进化 个人电脑 计算机 通过电话网络 进行连接 极客 利用技术 做一些有趣的尝试 极客文化 是 认真研究技术的 文化 计算机 不再是 高校和研究机构高墙里面的 神秘事物而是 生活中常见的 家用电器 ibm 蓝色巨人脚步沉重 dec 小型机不断蚕食低端市场甚至组成网络干掉大型机…...

crontab 执行脚本报错,手动执行脚本正常的解决方法
一、出现的问题 有一个守护脚本XXX.sh,需要使用oracle用户在linux上配置定时任务,每1分钟检查执行一次。但是发现该脚本使用oralce用户手动启动没问题,能正常把程序启动起来,而使用crontab并没有把程序启动起来。 二、排查分析问…...

扎心话题 | 设计院背后的潜规则你知道吗?
大家好,我是建模助手。 大家都知道,在过去的2022年经济是真难!以小编所在的广东为例,全年GDP增长仅1.9%。 这个数据足以呈现一个社会现象——不仅消费力咔咔下降,各行各业更有不同程度地嗝屁。这其中也包括一些设计院…...

【JavaEE初阶】第二节.多线程( 进阶篇 ) 锁的优化、JUC的常用类、线程安全的集合类
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、synchronized的优化操作 1.1 锁膨胀/锁升级 1.2 锁消除 1.3 锁粗化二、JUC 2.1 Callable接口 2.2 ReentrantLock类&…...

大数据核心技术是什么
大数据的核心层:数据采集层、数据存储与分析层、数据共享层、数据应用层,可能叫法有所不同本质上的角色都大同小异。 大数据的核心技术都包括什么? 1、数据采集 数据采集的任务就是把数据从各种数据源中采集和存储到数据存储上,…...

「TCG 规范解读」初识 TPM 2.0 库续一
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...

task与function
task和function主要是有助于代码的可重用性,都可以在module-endmodule之外声明。 1.function 1.1.function逻辑的综合 function:一个只有1个wire型输出值、全是组合逻辑的函数,且函数名即输出信号名,小括号中按顺序例化输入信号。…...
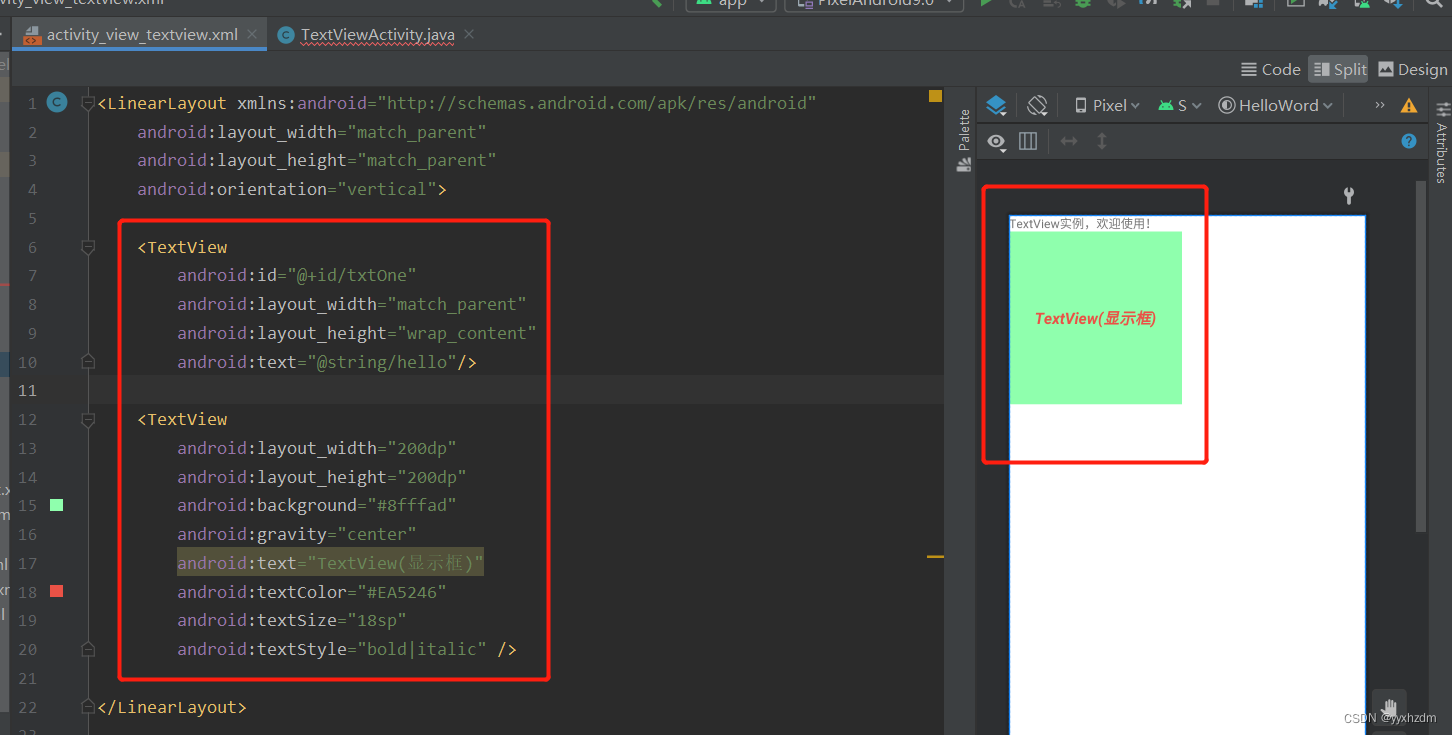
Android 基础知识4-3.1 TextView(文本框)详解
一、前言 TextView就是一个显示文本标签的控件,就是用来显示文本。可以在代码或者 XML中设置字体,字体大小,字体颜色 ,字体样式 (加粗级斜体),文字截断(比如:只显示10个字…...
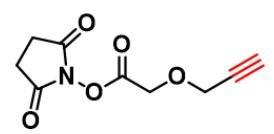
点击化学 PEG 试剂1858242-47-3,Propargyl丙炔基-PEG1-乙酸活性酯
Propargyl-PEG1-Acetic acid-NHS ester,丙炔基-聚乙二醇-乙酸琥珀酰亚胺酯,丙炔基-PEG1-乙酸活性酯,丙炔基-PEG1-乙酸-NHS 酯产品规格:1.CAS号:1858242-47-32.分子式:C9H9NO53.分子量:211.174.包…...

正则表达式是如何运作的?
在日常的开发工作当中,我们必不可免的会碰到需要使用正则的情况。 正则在很多时候通过不同的组合方式最后都可以达到既定的目标结果。比如我们有一个需要匹配的字符串: hello,我们可以通过 / .</p>/ 以及 / .?</p>/ 来匹配&…...

JVM参数GC线程数ParallelGCThreads设置
1. ParallelGCThreads参数含义JVM垃圾回收(GC)算法的两个优化标的:吞吐量和停顿时长。JVM会使用特定的GC收集线程,当GC开始的时候,GC线程会和业务线程抢占CPU时间,吞吐量定义为CPU用于业务线程的时间与CPU总消耗时间的比值。为了承…...

java 线程的那些事
什么是进程: 你把它理解成一个软件 什么是线程: 你把它理解成软件里面的一个功能,做的事情 什么是多线程: 你把它理解成 软件里面的某一个功能,原先是一个人累死累活的在那里完成,现在好了,多…...
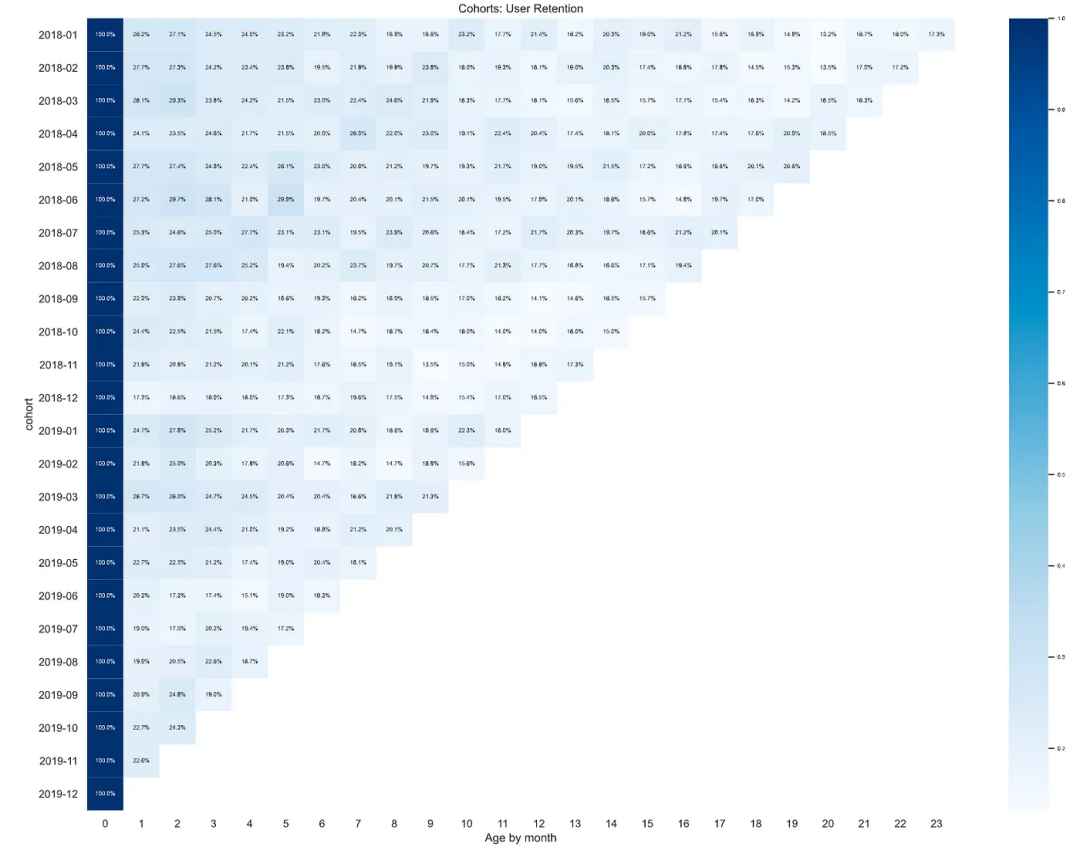
如何利用 Python 进行客户分群分析(附源码)
每个电子商务数据分析师必须掌握的一项数据聚类技能 如果你是一名在电子商务公司工作的数据分析师,从客户数据中挖掘潜在价值,来提高客户留存率很可能就是你的工作任务之一。 然而,客户数据是巨大的,每个客户的行为都不一样。20…...

D1s RDC2022纪念版开发板开箱评测及点屏教程
作者new_bee 本文转自:https://bbs.aw-ol.com/topic/3005/ 目录 芯片介绍开发板介绍RT-Smart用户态系统编译使用感想引用 1. 芯片介绍 RISC-V架构由于其精简和开源的特性,得到业界的认可,近几年可谓相当热门。操作系统方面有RT-Thread&am…...

了解一下TCP/IP协议族
在《简单说说OSI网络七层模型》中讲到,目前实际使用的网络模型是 TCP/IP 模型,它对 OSI 模型进行了简化,只包含了四层,从上到下分别是应用层、传输层、网络层和链路层(网络接口层),每一层都包含…...

【第十九部分】存储过程与存储函数
【第十九部分】存储过程与存储函数 文章目录【第十九部分】存储过程与存储函数19. 存储过程与存储函数19.1 存储过程19.2 创建、调用存储过程19.2.1 不带参数19.2.2 IN 类型19.2.3 OUT类型19.2.4 IN和OUT类型同时使用19.2.5 INOUT类型19.3 存储函数19.4 创建、调用存储函数19.5…...

字节序
字节序 字节序:字节在内存中存储的顺序。 小端字节序:数据的高位字节存储在内存的高位地址,低位字节存储在内存的低位地址 大端字节序:数据的低位字节存储在内存的高位地址,高位字节存储在内存的低位地址 bit ( 比特…...
PDF文件怎么转图片格式?转换有技巧
PDF文件有时为了更美观或者更直观的展现出效果,我们会把它转成图片格式,这样不论是归档总结还是存储起来都会更为高效。有没有合适的转换方法呢?这就来给你们罗列几种我个人用过体验还算不错的方式,大家可以拿来参考一下哈。1.用电…...
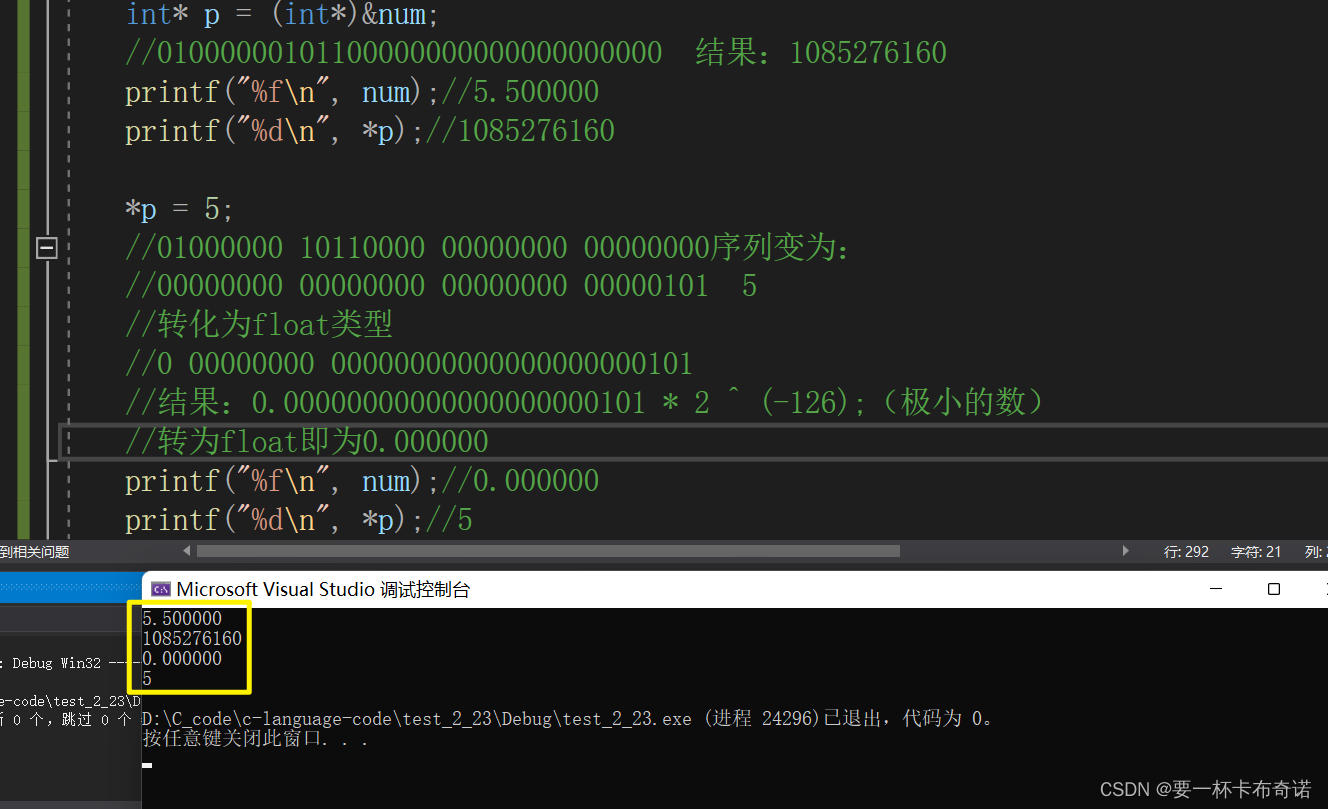
筑基七层 —— 数据在内存中的存储?拿来吧你
目录 零:移步 一.修炼必备 二.问题思考 三.整型在内存中的存储 三.大端字节序和小端字节序 四.浮点数在内存中的存储 零:移步 CSDN由于我的排版不怎么好看,我的有道云笔记相当的美观,请移步至有道云笔记 一.修炼必备 1.入门…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
