筑基七层 —— 数据在内存中的存储?拿来吧你
目录
零:移步
一.修炼必备
二.问题思考
三.整型在内存中的存储
三.大端字节序和小端字节序
四.浮点数在内存中的存储
零:移步
CSDN由于我的排版不怎么好看,我的有道云笔记相当的美观,请移步至有道云笔记
一.修炼必备
1.入门必备:VS2019社区版,下载地址:Visual Studio 较旧的下载 - 2019、2017、2015 和以前的版本 (microsoft.com)
2.趁手武器:印象笔记/有道云笔记
3.修炼秘籍:牛客网 - 找工作神器|笔试题库|面试经验|实习招聘内推,求职就业一站解决_牛客网 (nowcoder.com)
4.雷劫必备:leetcode 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
注:遇到瓶颈怎么办?百度百科_全球领先的中文百科全书 (baidu.com)
二.问题思考
1.C语言数据的类型?
2.整数在计算机中二进制的表示形式有几种?正整数和负整数相同的吗?
3.整数在内存中的存放的是什么?怎么验证是这样存放的?
4.为什么计算机中存放的是补码?
5.什么是字节序?
6.数据的字节序是在内存中怎么存储的?
7.如何判断一个数据的字节序是大端字节序还是小端字节序?
8.浮点数在内存中的存储和整数的存储是一样的吗?
9.浮点数的存储规则
三.整型在内存中的存储
1.C语言数据的类型?
1)整型:char,short,int,long,long long
2)浮点型:float,double
3)构造类型:struct,union
4)指针类型:int*,char*,double*等
5)空类型:void(常用于函数的返回类型,指针类型,函数的参数)
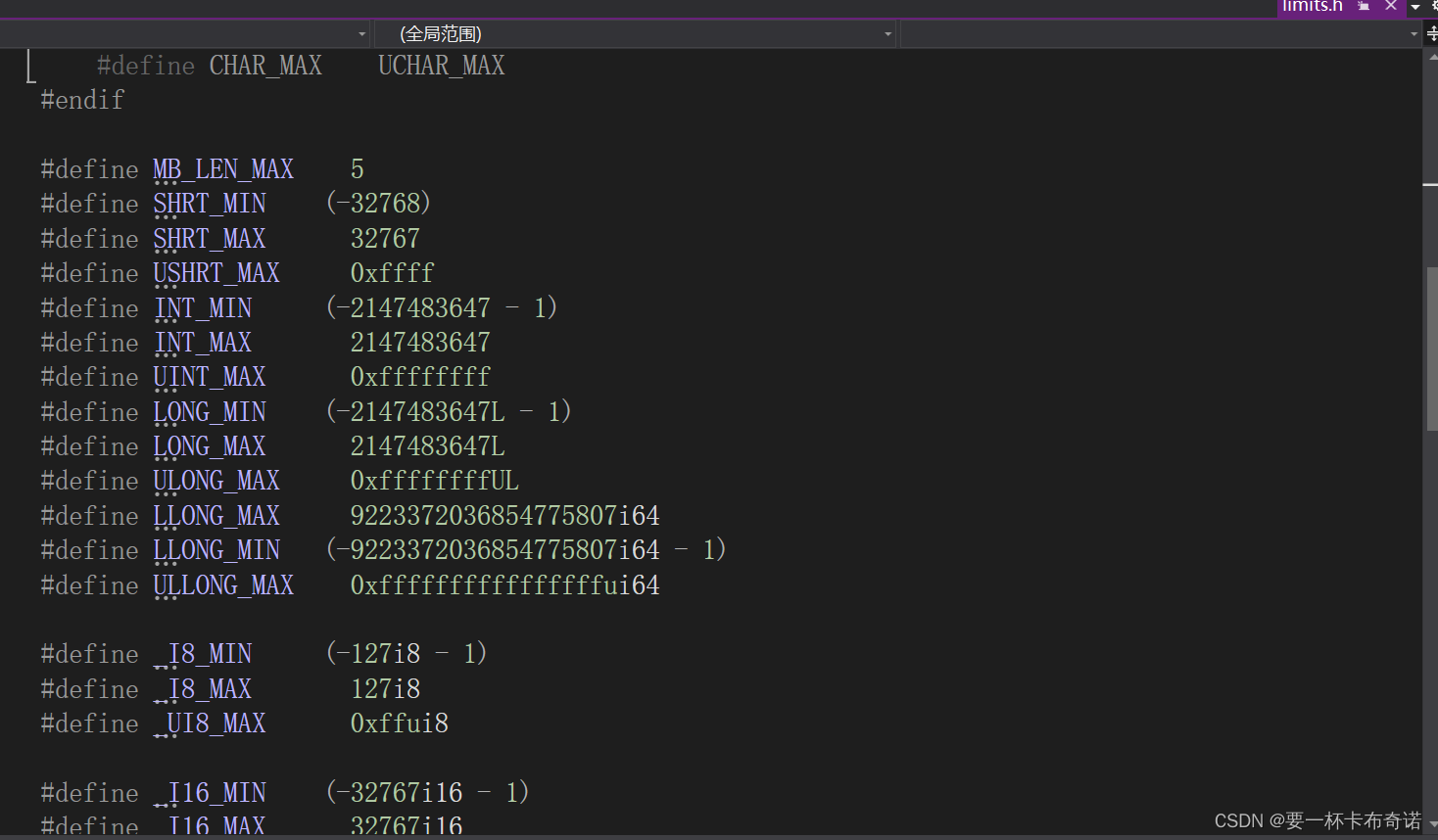
2.如何查看整数类型的值范围?
——在limits.h头文件中查看
3.整数在计算机中二进制的表示形式有几种?正整数和负整数相同的吗?
1)整数在计算机中的表示形式有:原码、反码、补码
2)正整数的原码、反码、补码均相同
3)负整数的原码、反码、补码的规则
原码:把整数直接按照二进制进行转化
反码:原码的符号位不变,其他位按位取反
补码:反码 + 1
#include <stdio.h>//原码、反码、补码的转化规则
int main()
{//正整数的原码、反码、补码相同int num1 = 5;//00000000 00000000 00000000 00000101 num1的补码//负整数的原码、反码、补码转化int num2 = -5;//10000000 00000000 00000000 00000101 原码//(原码符号位不变,其他位取反)//11111111 11111111 11111111 11111010 反码//(反码+1)//11111111 11111111 11111111 11111011 补码return 0;
}4.如何证明整型在内存中存储的是补码?
——使用负数证明
1)打印出负数的十六进制形式(十六进制是无符号的打印)
#include <stdio.h>//证明整型在内存中存储的是补码
int main()
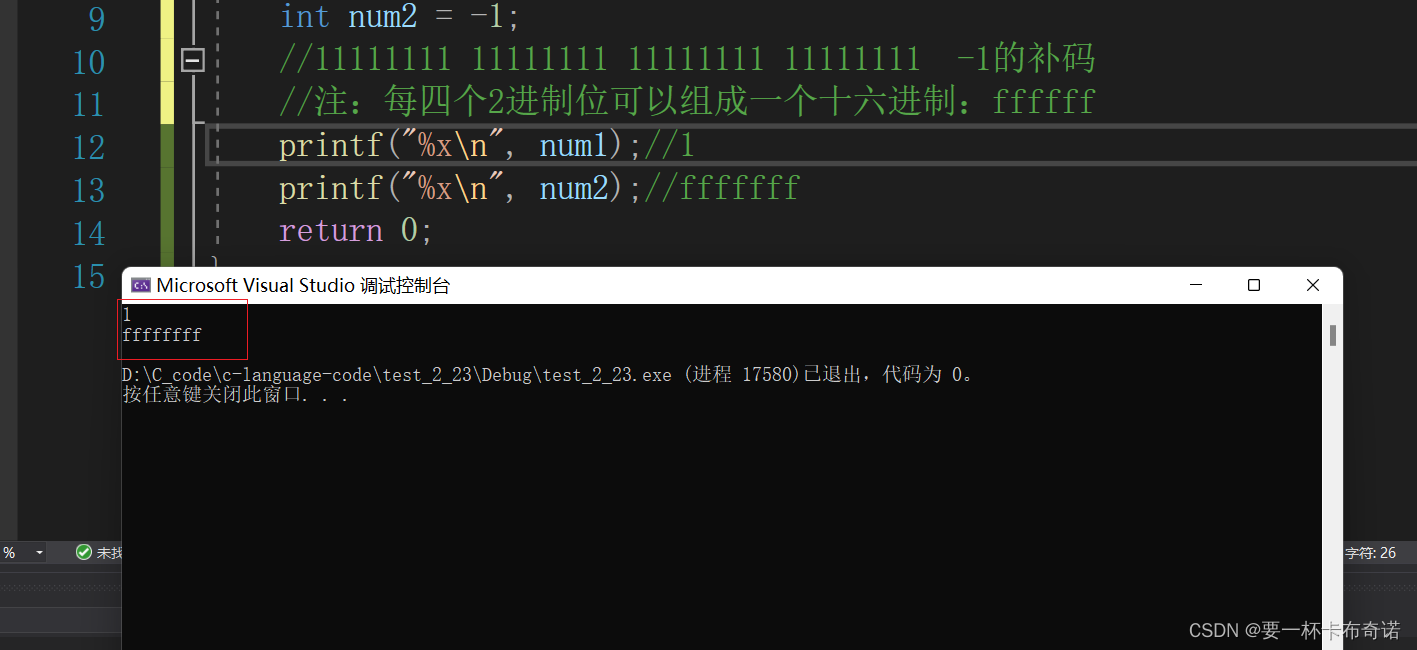
{int num1 = 1;//00000000 00000000 00000000 00000001 1的补码int num2 = -1;//11111111 11111111 11111111 11111111 -1的补码//注:每四个2进制位可以组成一个十六进制:ffffffprintf("%x\n", num1);//1printf("%x\n", num2);//fffffffreturn 0;
}运行结果如图:
2)调试查看负数在内存中的存储形式
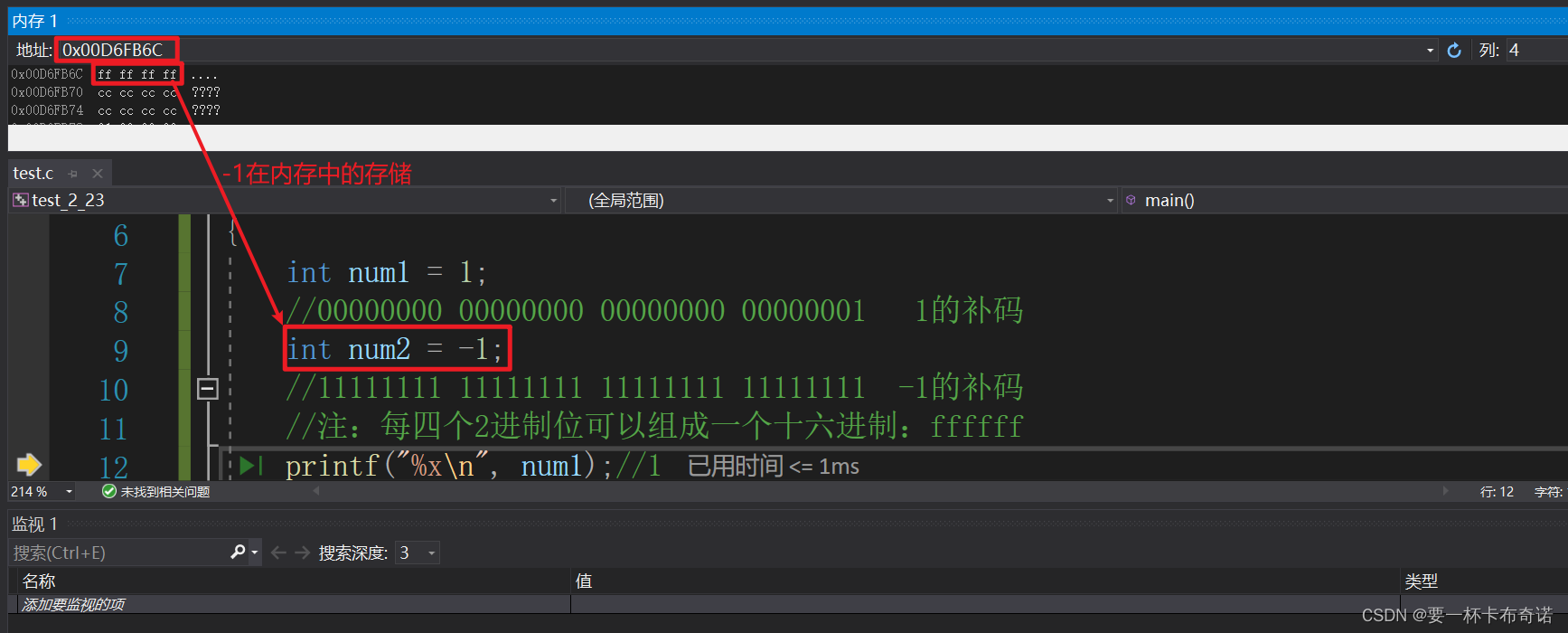
5.为什么计算机中存放的是补码?
1)方便运算:省去了计算机判断符号位或判断+/-运算的麻烦,采用补码后,不管是加法还是减法均是使用加法进行运算(CPU只有加法器)
2)更加标准:保证了系统的编码的一致性和连续性,也同时避免了+/-0的麻烦
6.practice
case 1:思考并分析
#include <stdio.h>int main()
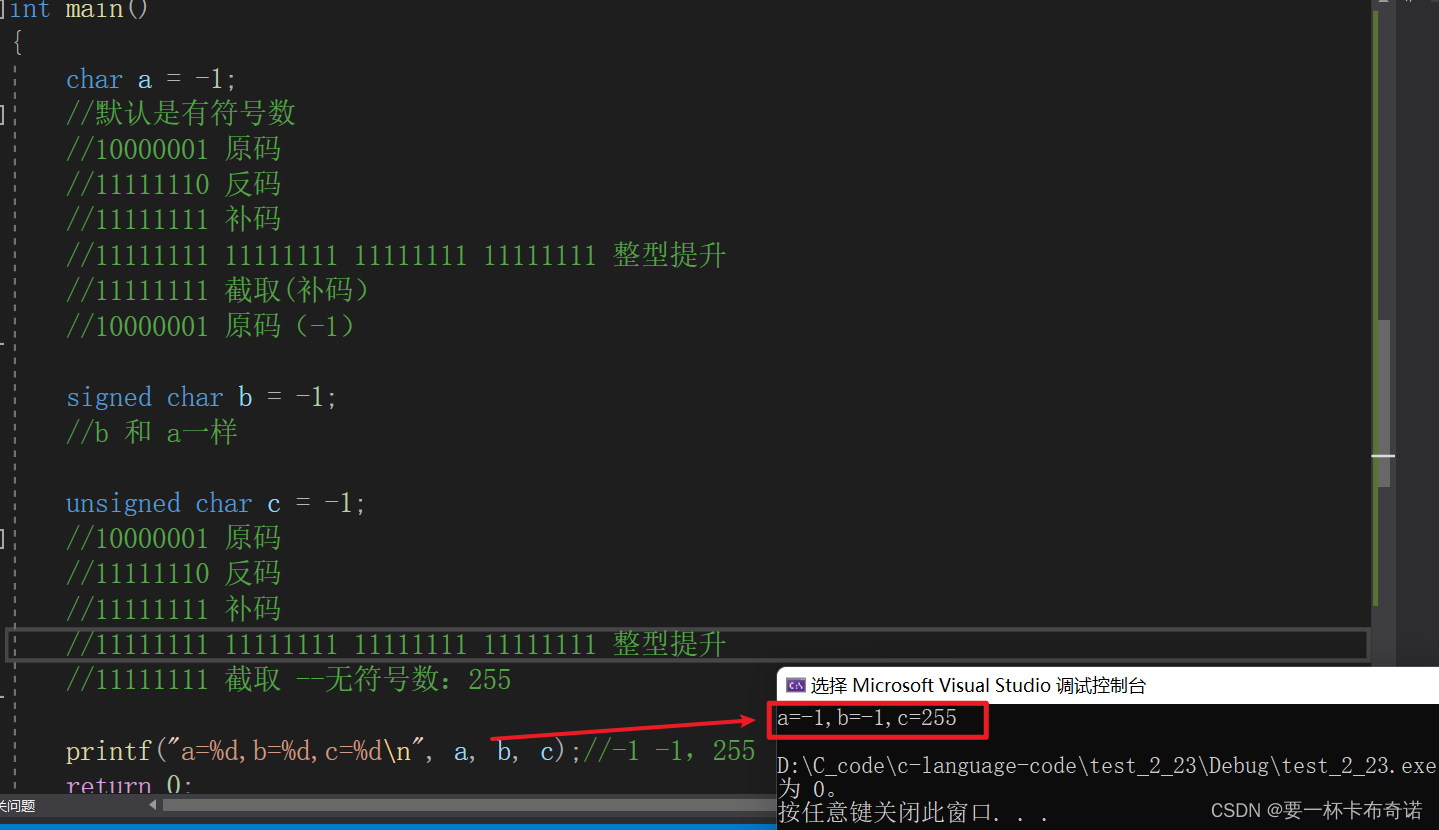
{char a = -1;//默认是有符号数//10000001 原码//11111110 反码//11111111 补码//11111111 11111111 11111111 11111111 整型提升//11111111 截取(补码)//10000001 原码(-1)signed char b = -1;//b 和 a一样unsigned char c = -1;//10000001 原码//11111110 反码//11111111 补码//11111111 11111111 11111111 11111111 整型提升//11111111 截取 --无符号数:255printf("a=%d,b=%d,c=%d\n", a, b, c);//-1 -1,255return 0;
}运行结果如图:
case 2:思考并分析
#include <stdio.h>int main()
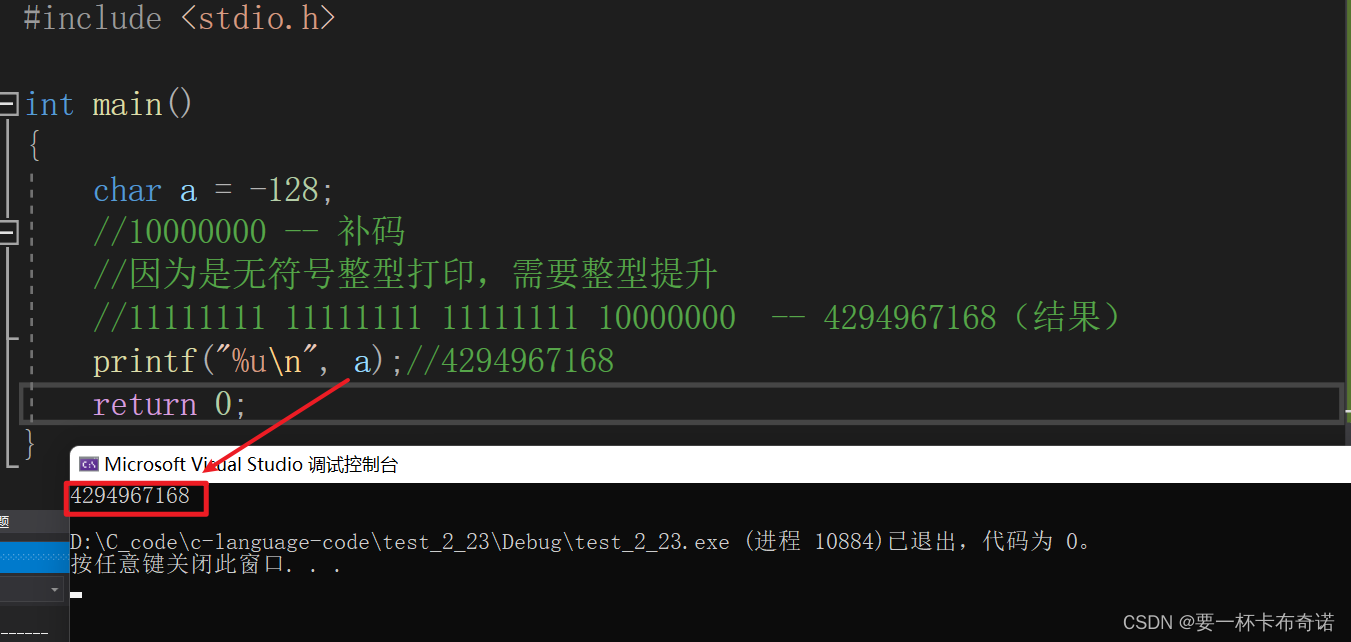
{char a = -128;//10000000 -- 补码//因为是无符号整型打印,需要整型提升//11111111 11111111 11111111 10000000 -- 4294967168(结果)printf("%u\n", a);//4294967168return 0;
}运行结果如图:
case 3:思考并分析
#include <stdio.h>int main()
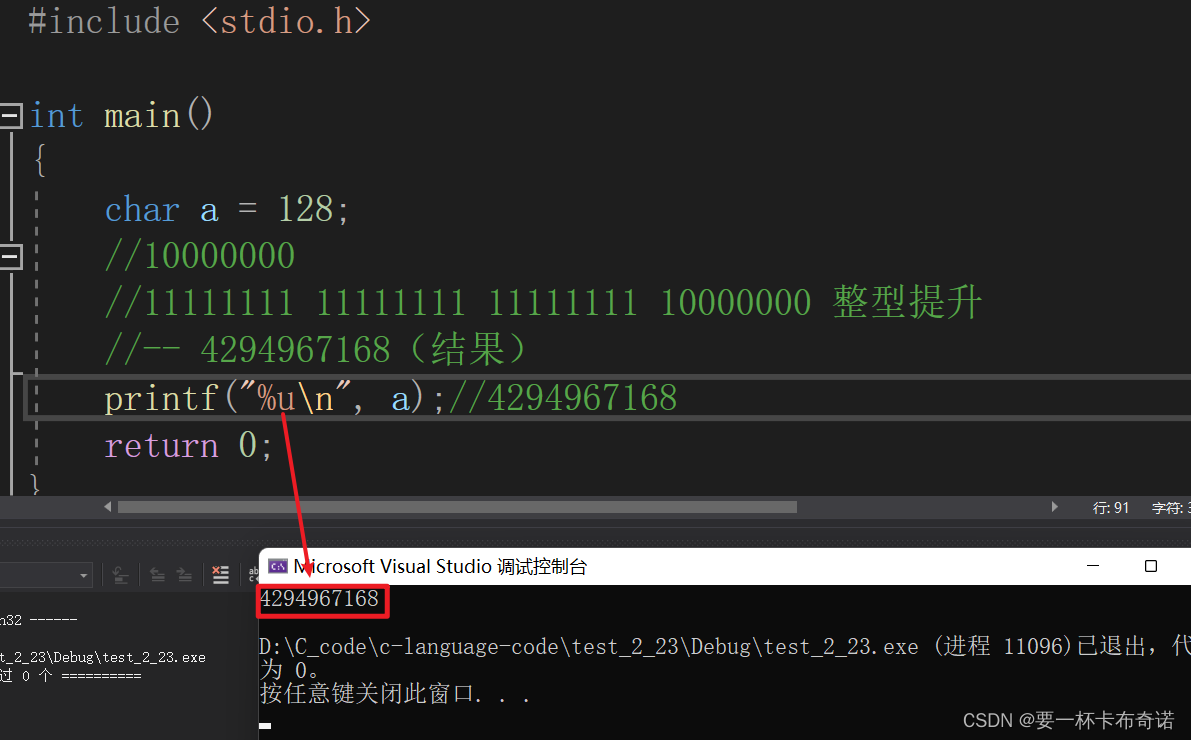
{char a = 128;//10000000//11111111 11111111 11111111 10000000 整型提升//-- 4294967168(结果)printf("%u\n", a);//4294967168return 0;
}运行结果如图:
case 4:思考并分析
#include <stdio.h>int main()
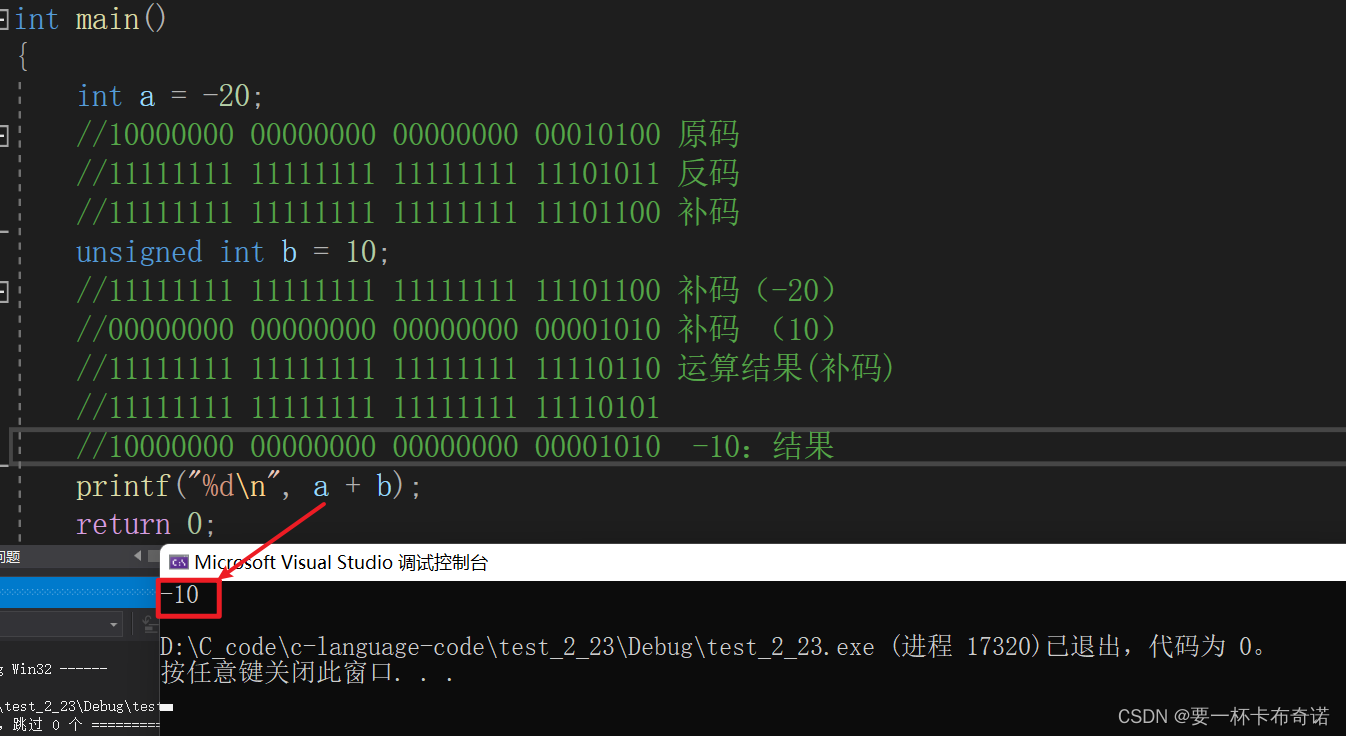
{int a = -20;//10000000 00000000 00000000 00010100 原码//11111111 11111111 11111111 11101011 反码//11111111 11111111 11111111 11101100 补码unsigned int b = 10;//11111111 11111111 11111111 11101100 补码(-20)//00000000 00000000 00000000 00001010 补码 (10)//11111111 11111111 11111111 11110110 运算结果(补码)//11111111 11111111 11111111 11110101//10000000 00000000 00000000 00001010 -10:结果printf("%d\n", a + b);return 0;
}运行结果如图:
case 5:思考并分析
#include <stdio.h>int main()
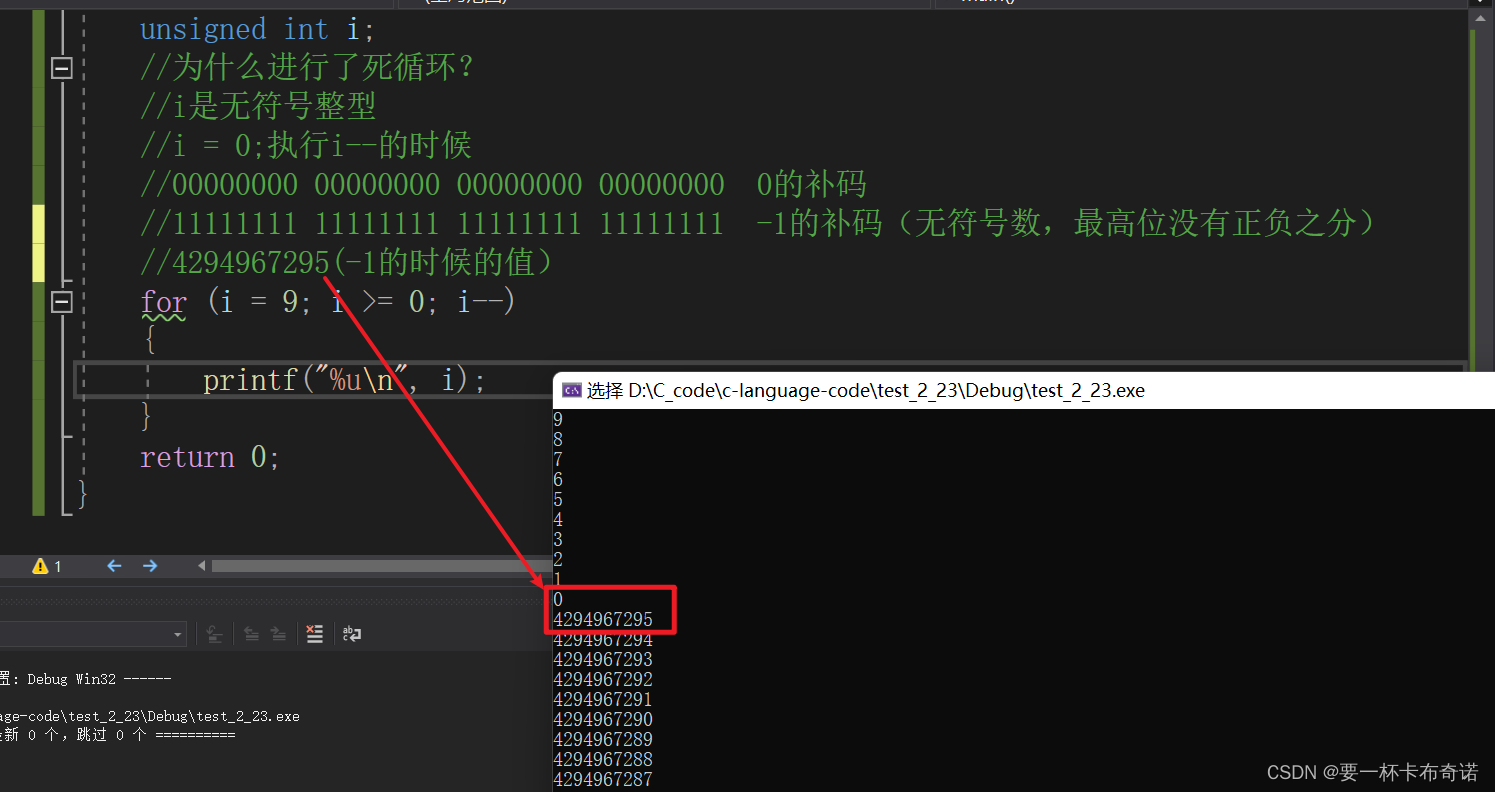
{unsigned int i;//为什么进行了死循环?//i是无符号整型//i = 0;执行i--的时候//00000000 00000000 00000000 00000000 0的补码//11111111 11111111 11111111 11111111 -1的补码(无符号数,最高位没有正负之分)//4294967295(-1的时候的值)for (i = 9; i >= 0; i--){printf("%u\n", i);}return 0;
}运行结果如图:
case 6:思考并分析
#include <stdio.h>
#include <string.h>int main()
{char a[1000];int i;for (i = 0; i < 1000; i++){a[i] = -1 - i;//11111111 -1的补码//11111110 -2的补码//11111101 -3的补码//……//10000000 -128的补码//01111111 127的补码//……//00000000 0的补码('\0')}printf("%d\n", strlen(a));//255return 0;
}一图了解char的范围:
运行结果如图:
 case 7:思考并分析
case 7:思考并分析
#include <stdio.h>unsigned char i;
int main()
{for (i = 0; i <= 255; i++){printf("hehe\n");//11111111 i为255的时候//00000000 255+1后的值//所以为死循环}return 0;
}运行结果如图:
三.大端字节序和小端字节序
1.什么是字节序?
——字节序又称为端序或尾序,指计算机内存中多字节数据在内存中的排列顺序
2.数据的字节序是在内存中怎么存储的?
——浮点数和整数的字节序都有大端和小端两种字节序
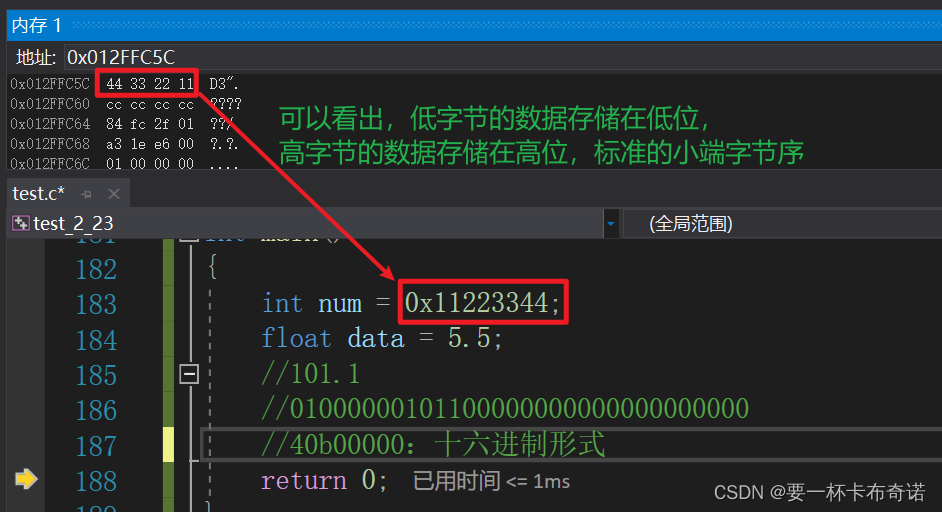
1)小端字节序
——数据的低位字节存储在内存的低地址处,高位字节存储在内存的高地址处
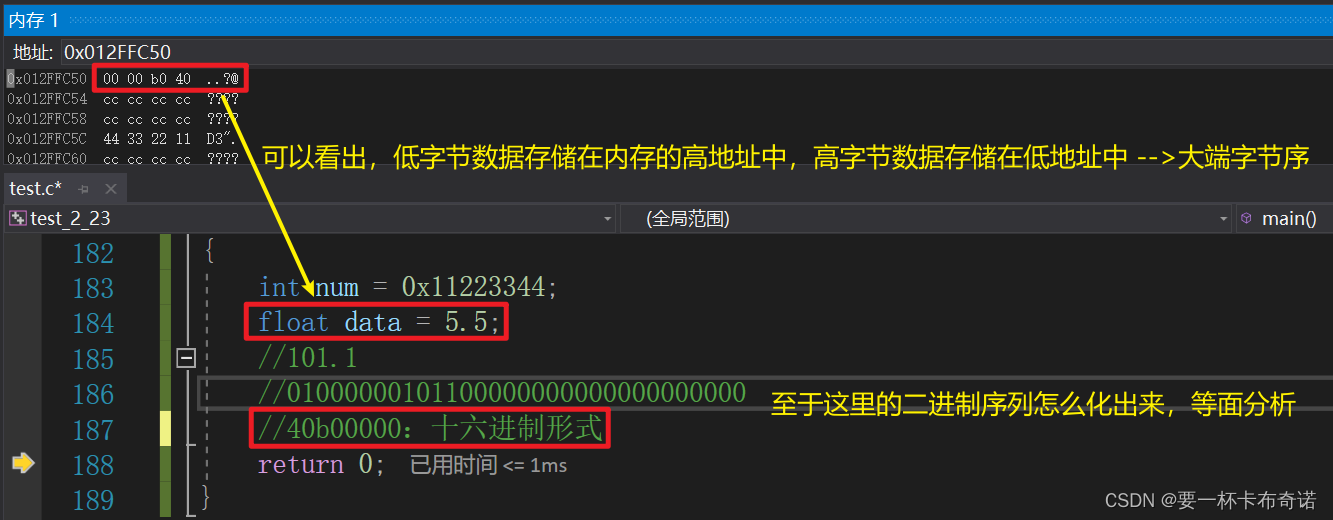
2)大端字节序
——数据的低位字节存储在内存的高地址处,高位字节存储在内存的低地址处
3.如何判断一个数据的字节序是大端字节序还是小端字节序?
——内存中查看该数据的存储形式,看低位存放在内存中的位置
图解:
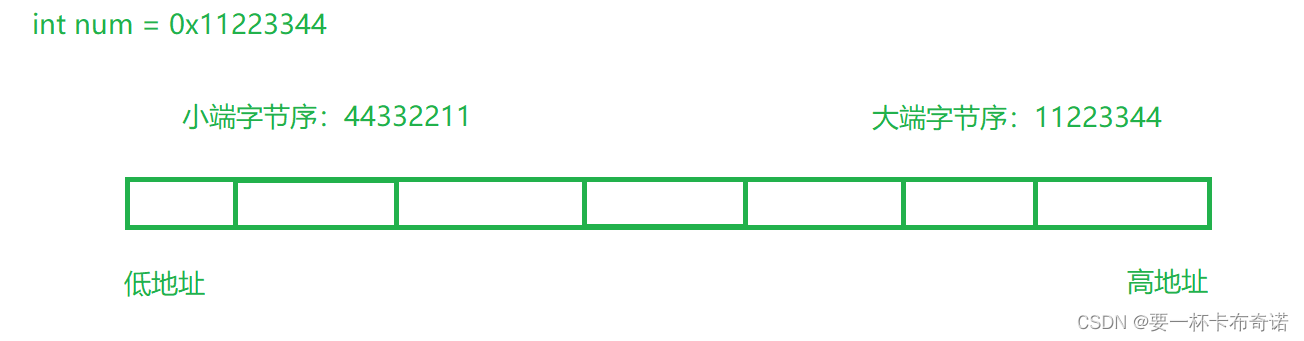
代码解释:
#include <stdio.h>int main()
{int num = 0x11223344;float data = 5.5;//101.1//01000000101100000000000000000000//40b00000:十六进制形式return 0;
}小端字节序在内存中的图解:
大端字节序在内存中的图解:
4.一道笔试题加强巩固
——请判断一个机器是大端字节序还是小端字节序
思路分析:我们只需要判断取出1的最低位即可,如果是0,则是大端存储序列,如果是1,则是小端字节序
#include <stdio.h>//判断当前机器是大端还是小端字节序
int main()
{int a = 1;char* p = (char*)&a;if (*p == 1){printf("小端字节序\n");}else{printf("大端字节序\n");}return 0;
}代码是写出来了,但是这样写是不是有点太low了,我们换种方式
#include <stdio.h>//判断当前机器是大端还是小端字节序
int judge(int a)
{char* p = (char*)&a;return *p;//如果小端,直接返回1,大端返回0
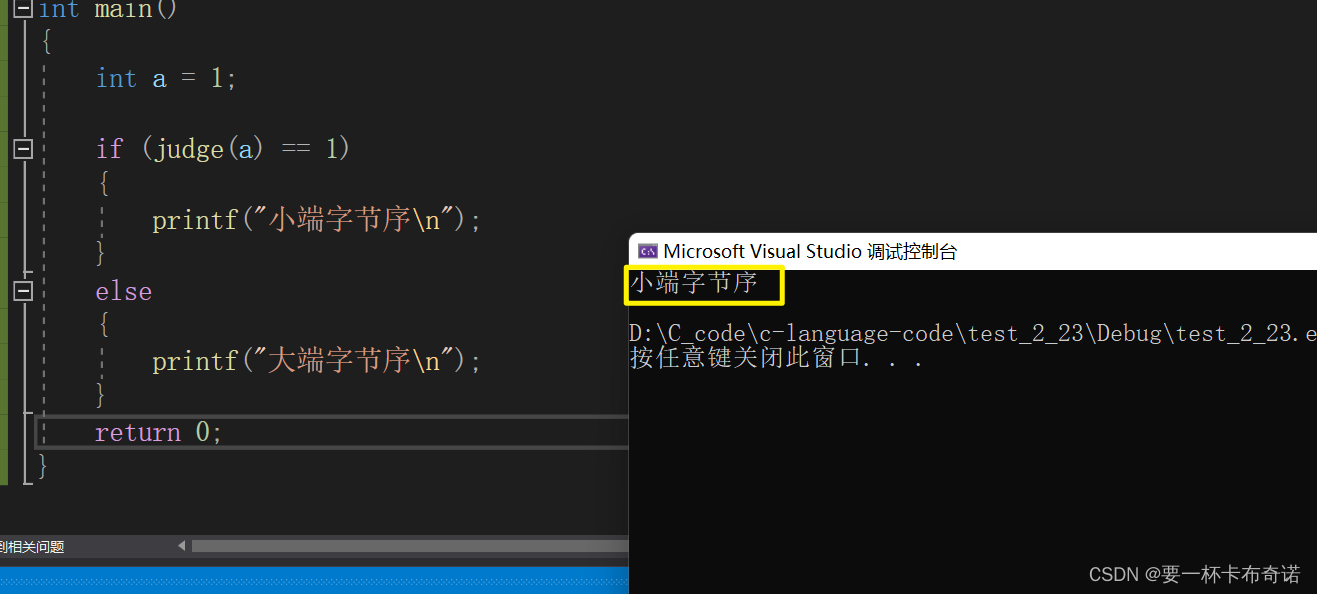
}int main()
{int a = 1;if (judge(a) == 1){printf("小端字节序\n");}else{printf("大端字节序\n");}return 0;
}运行结果如图:
四.浮点数在内存中的存储
1.怎么查看浮点数的值范围?
——在float.h头文件中查看
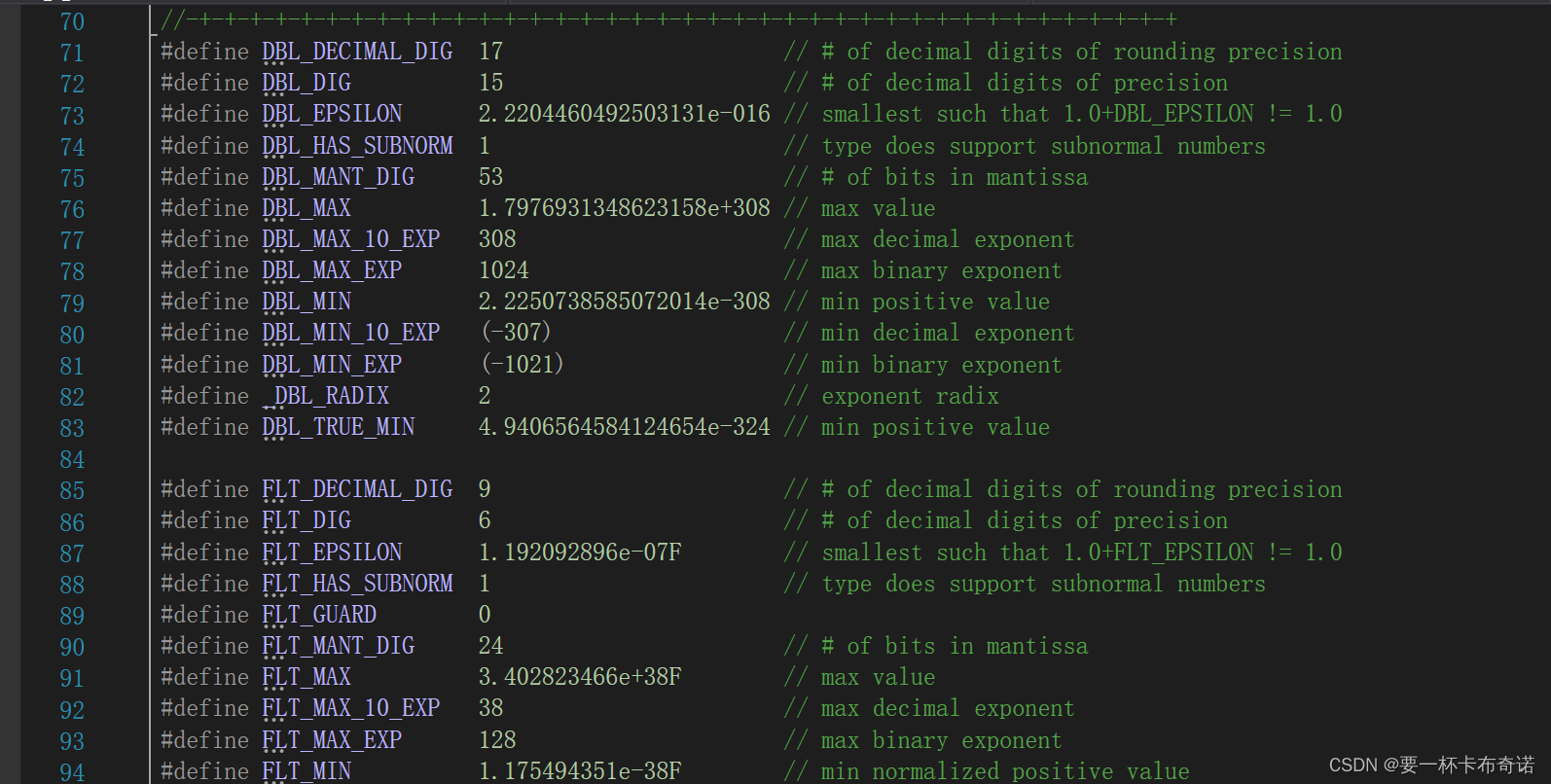
2.浮点数的存储规则
1)浮点数进行存储的形式:(-1)^S * M * 2^E;
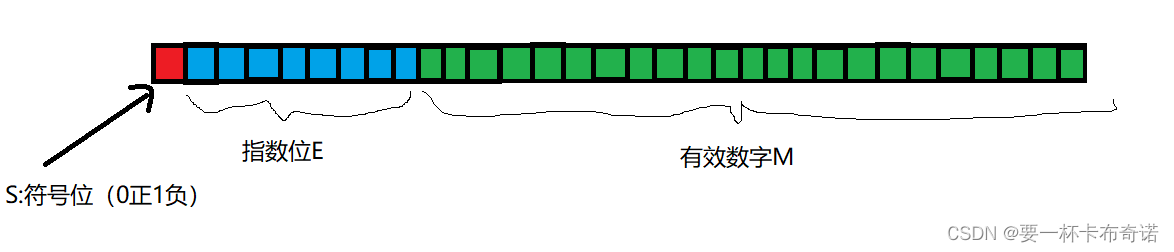
——解释:S表示符号位,M表示有效数字:1
2)在IEEE的规定下,最高位的1位S表示符号位,接下来的八位表示指数E,剩下的23位表示有效数字M
float图解:
double图解:
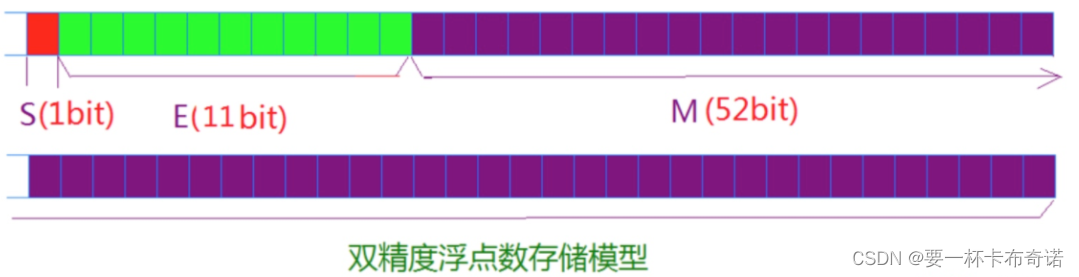
3)由图知:float的指数位有8位,double的指数位有11位,float的M有23位,double的M有52位
4)IEEE对M和E还有一些特别的规定
i.因为1
ii.指数E是一个无符号整数(unsigned int)
a.float的话,E的值在0~255之间;double的话,E的值在0~2047之间
b.注意,科学计数法中的E是可以是为负数的,所以我们在计算E的时候,应该加上一个中间值,float类型+127,double类型+1023
iii.E从内存中取出的三种情况
a.E不为全0或全1
——使用E转化的十进制值减去127/1023得到真实值,在给有效数字加上小数点前面的1(常用)
b.E全为0
——E的值是1-127或1-1023,得到真实值,这个时候我们不需要在加上小数点前面的1了,这样做是为了表示正负0,以及接近0的很小的数值
c.E全为1
——这时,如果有效数字全为0,表示±无穷大(正负取决于符号位s)
3.practice
case 1:分析解释下面代码
#include <stdio.h>int main()
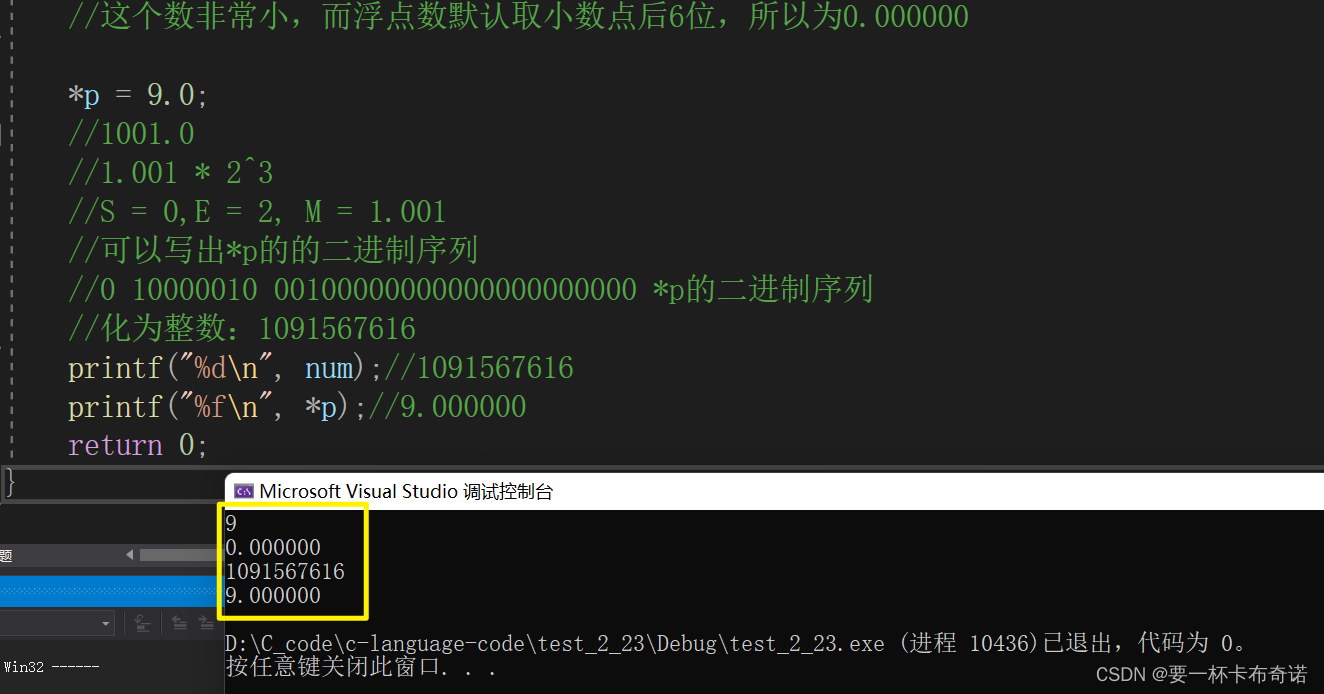
{int num = 9;float* p = (float*)#printf("%d\n", num);//9printf("%f\n", *p);//0.000000//分析为什么是0.000000//00000000 00000000 00000000 00001001 9的补码//浮点数中看到的形式//0 00000000 00000000000000000001001//相当于0.00000000000000000001001 * (1 - 2^-126)//这个数非常小,而浮点数默认取小数点后6位,所以为0.000000*p = 9.0;//1001.0//1.001 * 2^3//S = 0,E = 2, M = 1.001//可以写出*p的的二进制序列//0 10000010 00100000000000000000000 *p的二进制序列//化为整数:1091567616printf("%d\n", num);//1091567616printf("%f\n", *p);//9.000000return 0;
}运行结果如图:
case 2:分析并解释
#include <stdio.h>int main()
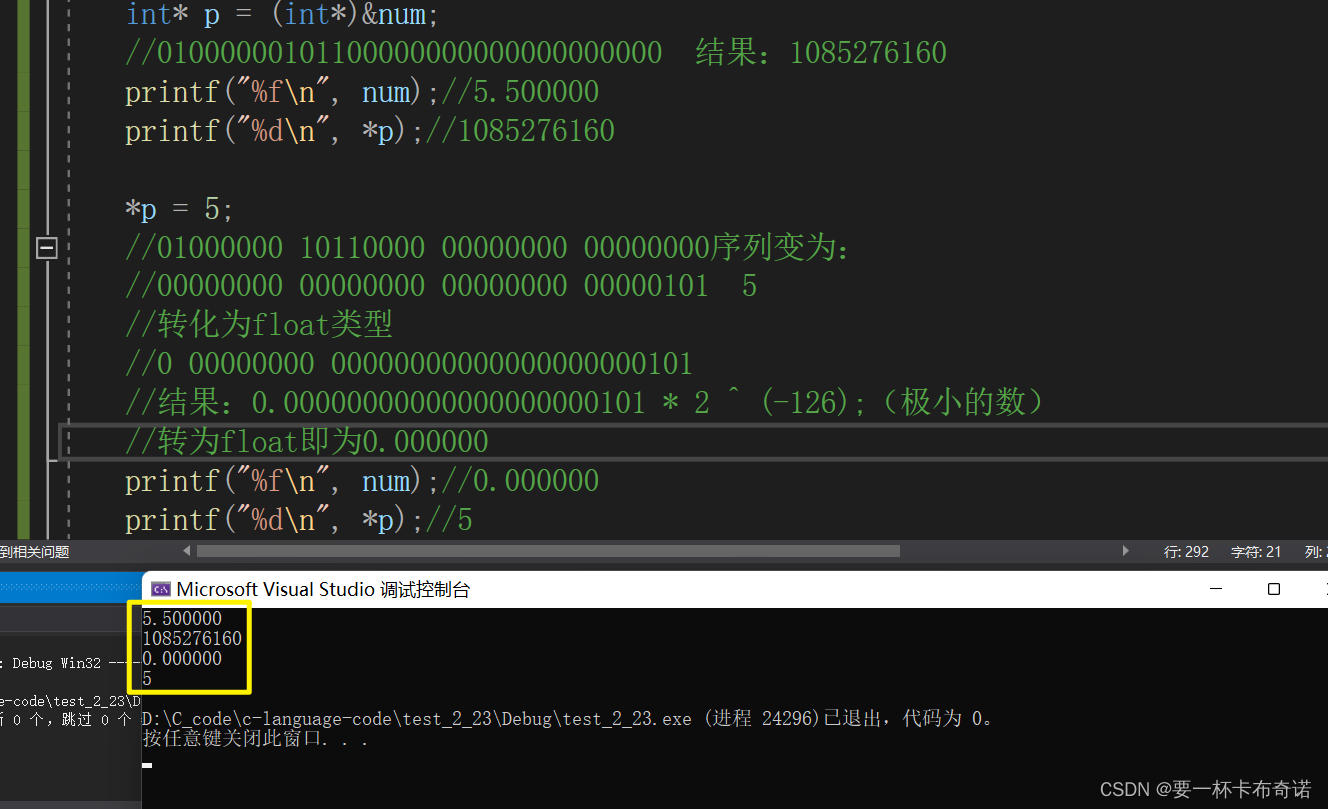
{float num = 5.5;//101.1 --> 1.011//S = 0,E = 2, M = 1.011 --> 得出二进制序列//0 10000001 01100000000000000000000 num的二进制序列int* p = (int*)#//01000000101100000000000000000000 结果:1085276160printf("%f\n", num);//5.500000printf("%d\n", *p);//1085276160*p = 5;//01000000 10110000 00000000 00000000序列变为://00000000 00000000 00000000 00000101 5//转化为float类型//0 00000000 00000000000000000000101 //结果:0.00000000000000000000101 * 2 ^ (-126);(极小的数)//转为float即为0.000000printf("%f\n", num);//0.000000printf("%d\n", *p);//5return 0;
}运行结果如图:
!!!恭喜你,突破至筑基七层!!!
相关文章:

筑基七层 —— 数据在内存中的存储?拿来吧你
目录 零:移步 一.修炼必备 二.问题思考 三.整型在内存中的存储 三.大端字节序和小端字节序 四.浮点数在内存中的存储 零:移步 CSDN由于我的排版不怎么好看,我的有道云笔记相当的美观,请移步至有道云笔记 一.修炼必备 1.入门…...
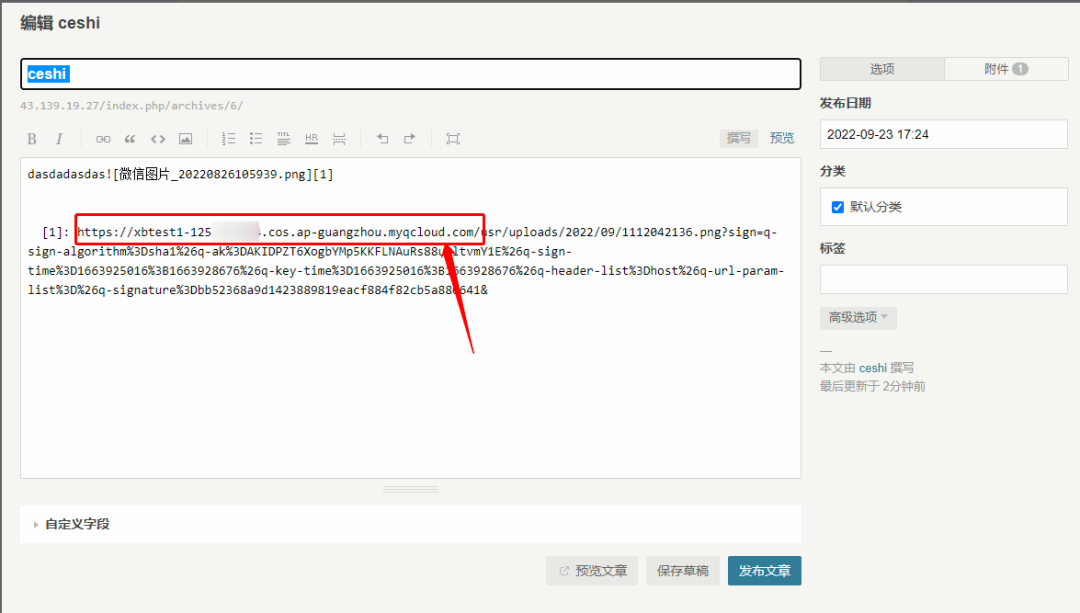
Typecho COS插件实现网站静态资源存储到COS,降低本地存储负载
Typecho 简介Typecho 是一个简单、强大的轻量级开源博客平台,用于建立个人独立博客。它具有高效的性能,支持多种文件格式,并具有对设备的响应式适配功能。Typecho 相对于其他 CMS 还有一些特殊优势:包括可扩展性、不同数据库之间的…...
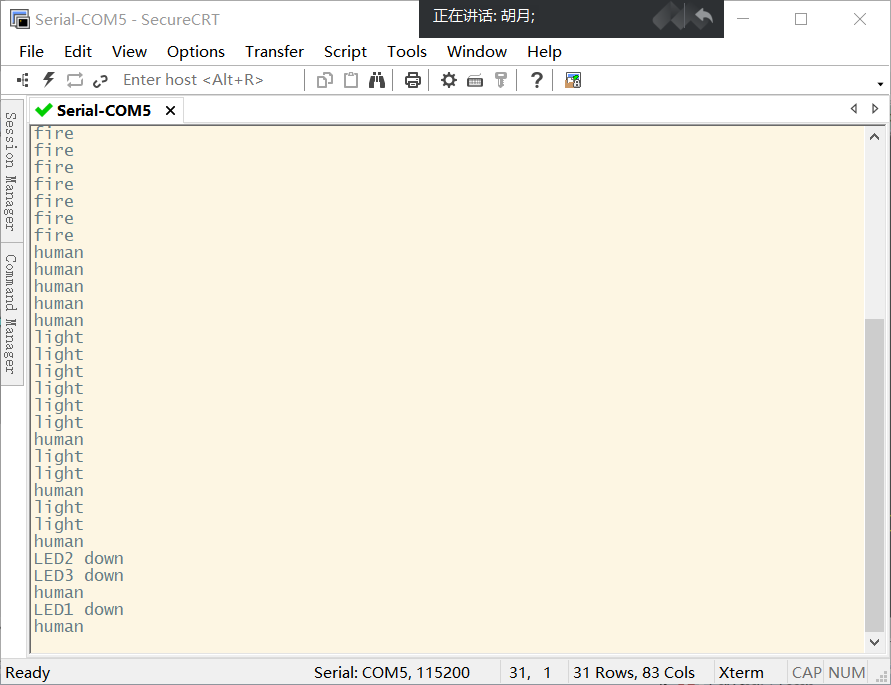
2月23号作业
题目:题目一:通过操作Cortex-A7核,串口输入相应的命令,控制LED灯进行工作--->上传CSDN 1.例如在串口输入led1on,开饭led1灯点亮 2.例如在串口输入led1off,开饭led1灯熄灭 3.例如在串口输入led2on,开饭led2灯点亮 4.例如在串口输…...
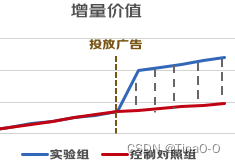
因果推断方法(一)合成控制
知道的跳过下面的简单介绍: 就是比如广告主投放了10w元,那么他的收益怎么算?哪些订单就是广告带来的,哪些是不放广告也会购买? 合成控制法是目前我实际应用发现最好用的。置信度高,且容易理解。 简单讲下思…...
)
数据结构第12周 :( 有向无环图的拓扑排序 + 拓扑排序和关键路径 + 确定比赛名次 + 割点 )
目录有向无环图的拓扑排序拓扑排序和关键路径确定比赛名次割点有向无环图的拓扑排序 【问题描述】 由某个集合上的一个偏序得到该集合上的一个全序,这个操作被称为拓扑排序。偏序和全序的定义分别如下:若集合X上的关系R是自反的、反对称的和传递的&…...
)
Linux安装docker(无网)
1. 下载Docker安装包 下载地址:https://download.docker.com/linux/static/stable/x86_64/ 如果服务器可以联网可以通过wget下载安装包 wget https://download.docker.com/linux/static/stable/x86_64/docker-18.06.3-ce.tgz2. 解压安装 tar -zxvf docker-18.06…...

解决JNI操作内核节点出现写操作失败的问题
Android 9.0下,因为采取了SEAndroid/SElinux的安全机制,即使拥有root权限,或者对某内核节点设置为777的权限,仍然无法在JNI层访问。 本文将以用户自定义的内核节点/dev/wf_bt为例,手把手教会读者如何在JNI层获得对该节…...

纵然是在产业互联网的时代业已来临的大背景下,人们对于它的认识依然是短浅的
纵然是在产业互联网的时代业已来临的大背景下,人们对于它的认识依然是短浅的。这样一种认识的最为直接的结果,便是我们看到了各式各样的产业互联网平台的出现。如果一定要找到这些互联网平台的特点的话,以产业端为出发点,无疑是它…...

干翻 nio ,王炸 io_uring 来了 !!(图解+史上最全)
大趋势:全链路异步化,性能提升10倍 随着业务的发展,微服务应用的流量越来越大,使用到的资源也越来越多。 在微服务架构下,大量的应用都是 SpringCloud 分布式架构,这种架构总体上是全链路同步模式。 全链…...
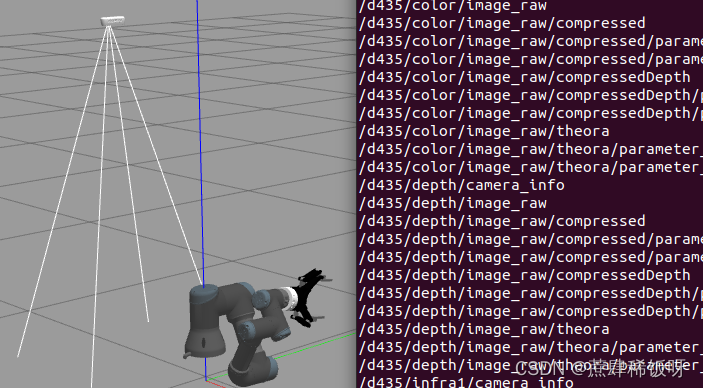
ur3+robotiq ft sensor+robotiq 2f 140+realsense d435i配置rviz,gazebo仿真环境
ur3robotiq ft sensorrobotiq 2f 140realsense d435i配置rviz,gazebo仿真环境 搭建环境: ubuntu: 20.04 ros: Nonetic sensor: robotiq_ft300 gripper: robotiq_2f_140_gripper UR: UR3 reasense: D435i 通过下面几篇博客配置好了ur3、力传…...

ASP.NET Core MVC 项目 AOP之Authorization
目录 一:说明 二:传统鉴权授权的基本配置 三 :角色配置说明 四:策略鉴权授权 五:策略鉴权授权Requirement扩展 总结 一:说明 鉴权:是指验证你是否登录,你登录后的身份是什么。…...
智能新冠疫苗接种助手管理系统
项目背景介绍 近几年来,网络事业,特别是Internet发展速度之快是任何人都始料不及的。目前,由于Internet表现出来的便捷,快速等诸多优势,已经使它成为社会各行各业,甚至是平民大众工作,生活不可缺少的一个重…...

Python+Selenium4元素交互1_web自动化(5)
目录 0. 上节回顾 1. 内置的等待条件 2. 元素属性 1. Python对象属性 2. HTML元素属性 3. 元素的交互 1. 输入框 2. 按钮 3. 单选框和复选框 0. 上节回顾 DEBUG的方式:JS断点 Python断点编程语言提供的等待方式:sleepselenium提供的等待方式&…...

2023双非计算机硕士应战秋招算法岗之深度学习基础知识
word版资料自取链接: 链接:https://pan.baidu.com/s/1H5ZMcUq-V7fxFxb5ObiktQ 提取码:kadm 卷积层 全连接神经网络需要非常多的计算资源才能支撑它来做反向传播和前向传播,所以说全连接神经网络可以存储非常多的参数,…...

Python opencv进行矩形识别
Python opencv进行矩形识别 图像识别中,圆形和矩形识别是最常用的两种,上一篇讲解了圆形识别,本例讲解矩形识别,最后的结果是可以识别出圆心,4个顶点,如下图: 左边是原始图像,右边是识别结果,在我i5 10400的CPU上,执行时间不到8ms。 识别出结果后,计算任意3个顶点…...

网安入门必备的12个kali Linux工具
kali Linux工具帮你评估 Web 服务器的安全性,并帮助你执行黑客渗透测试。 注意:这里不是所提及的所有工具都是开源的。 1. Nmap Nmap ( 网络映射器 )是一款用于 网络发现 和 安全审计 的 网络安全 工具. 主机发现,端口扫描,版本…...
【测试面试】头条大厂,测试开发岗真实一面。你能抵得住吗?
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 小吴: 现…...
分享app的测试技巧
前言 今天笔者想和大家来唠唠app测试,现在的app有非常的多,这些app都是需要经过测试之后才能发布到应用市场中,app已经成为了我们日常生活中不可或缺的一部分了,但它的功能必须强大,才能受到消费者的重视,…...

HTML 基础【快速掌握知识点】
目录 一、什么是HTML? 二、HTML的发展史 三、HTML5的优势 四、HTML基本结构 五、DOCTYPE声明 六、title标签 七、meta标签 八、标题标签 九、段落标签 十、换行标签 十一、水平线标签 十二、字体样式标签 十三、特殊符号 十四、图像标签 十五、链接标…...
SpringBoot入门(二)
这里写目录标题一、SpringBoot整合Junit1.1 搭建SpringBoot工程1.2 引入starter-test起步依赖1.3 编写类1.4 测试二、SpringBoot整合mybatis2.1 搭建SpringBoot工程2.2 引入mybatis起步依赖,添加驱动2.3 编写DataSource和MyBatis相关配置2.4 定义表和实体类2.5 编写…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
