数论知识点总结(一)
文章目录
目录
文章目录
前言
一、数论有哪些
二、题法混讲
1.素数判断,质数,筛法
2.最大公约数和最小公倍数
3.快速幂
4.约数
前言
现在针对CSP-J/S组的第一题主要都是数论,换句话说,持数论之剑,可行天下矣!
一、数论有哪些
数论 原根,素数判断,质数,筛法最大公约数,gcd扩展欧几里德算法,快速幂,exgcd,不定方程,进制,中国剩余定理,CRT,莫比乌斯反演,逆元,Lucas 定理,类欧几里得算法,调和级数,欧拉降幂......
但是,可但是,但可是,我是个蒟蒻,只能胜任很简单的数论和算法,今天只是做个考前复习罢了
二、题法混讲
1.素数判断,质数,筛法
(1)素数,质数的定义:只能被一和他本身整除的正整数教素数,又称质数(2是素数,0和1却不是)
(2)判定
代码如下(示例):
bool isprime(int n){if(n<2) return false;int x=sqrt(n);for(int i=2;i<=x;i++)if(n%i==0) return false;return true;
}(3)埃氏筛
代码如下(示例):
void get_primes(int n){for(int i=2;i<=n;i++){if(!flag[i]){p[++cnt]=i; for(int j=1;p[j]<=n/i;j++){flag[p[j]*i]=true;}}}
}(4)线性筛
代码如下(示例):
void get_primes(int n){for(int i=2;i<=n;i++){if(!flag[i]){p[++cnt]=i;for(int j=1;p[j]<=n/i;j++){flag[p[j]*i]=true;if(i%p[j]==0) break;}}}
}2.最大公约数和最小公倍数
代码如下(示例):
int gcd(int x,int y){if(y==0) return x;return gcd(y,x%y);
}
int lcm(int x,int y){return x*y/gcd(x,y);
}3.快速幂
递归写法:
int ksm(int a,int b,int mod){if(!b) return 1;int t=ksm(a,b>>1,mod);return (LL)(b&1?a:1)*t%mod*t%mod;
}非递归写法:
①
int ksm(int a,int b,int mod){int res=1;while(b){if(b&1) res=(LL)res*a%mod;a=a*a%mod;b>>=1;}return res;
}
②
int ksm(int a,int b,int mod){int ans=1;for(;b;a*=a,a%=mod,b>>=1)if(b&1) ans*=a,ans%=mod;return ans;
}4.约数
代码如下(实例):
vector<int> d;
void solve(int n){d.clear();for(int i = 1; i <= n / i; i ++){if(n % i == 0){d.push_back(i);if(i != n / i) d.push_back(n / i);}}sort(d.begin(), d.end());for(auto x : d) cout << x << " ";
}祝大家CSP-J/S,RP++
相关文章:
)
数论知识点总结(一)
文章目录 目录 文章目录 前言 一、数论有哪些 二、题法混讲 1.素数判断,质数,筛法 2.最大公约数和最小公倍数 3.快速幂 4.约数 前言 现在针对CSP-J/S组的第一题主要都是数论,换句话说,持数论之剑,可行天下矣! 一、数论有哪些 数论 原根,素数判断,质数,筛法最大公约数…...

知识分享 钡铼网关功能介绍:使用SSLTLS 加密,保证MQTT通信安全
背景 为了使不同的设备或系统能够相互通信,让旧有系统和新的系统可以集成,通信更加灵活和可靠。以及将数据从不同的来源收集并传输到不同的目的地,实现数据的集中管理和分发。 通信网关完美克服了这一难题,485或者网口的设备能通过…...

asp.net core mvc区域路由
ASP.NET Core 区域路由(Area Routing)是一种将应用程序中的路由划分为多个区域的方式,类似于 MVC 的控制器和视图的区域划分。区域路由可以帮助开发人员更好地组织应用程序的代码和路由,并使其更易于维护。 要使用区域路由&#…...
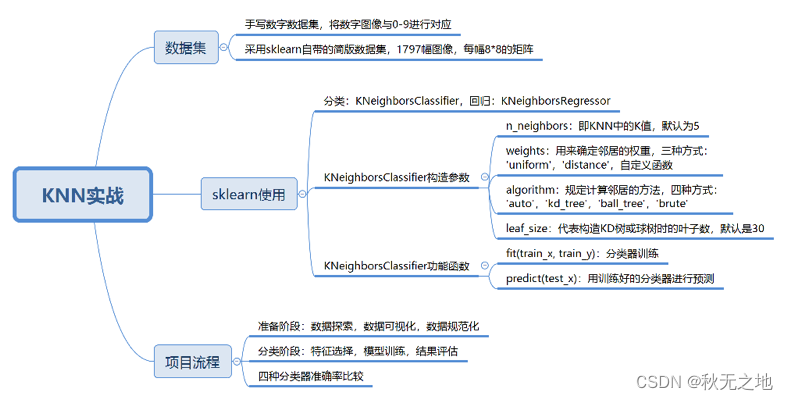
KNN(下):数据分析 | 数据挖掘 | 十大算法之一
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...

Servlet开发-session和cookie理解案例-登录页面
项目展示 进入登录页面,输入正确的用户名和密码以后会自动跳到主页 登录成功以后打印用户名以及上次登录的时间,如果浏览器和客户端都保存有上次登录的信息,则不需要登录就可以进入主页 编码思路 1.首先提供一个登录的前端页面&…...
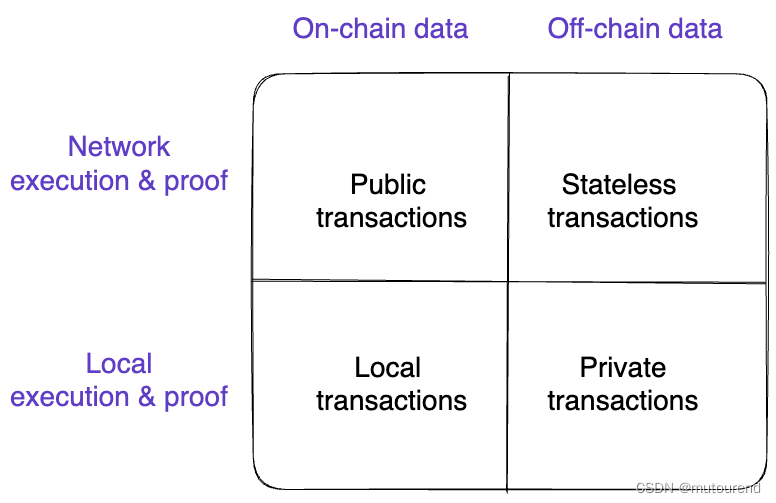
Polygon Miden:扩展以太坊功能集的ZK-optimized rollup
1. 引言 Polygon Miden定位为zkVM,定于2023年Q4上公开测试网。 zk、zkVM、zkEVM及其未来中指出,当前主要有3种类型的zkVM,括号内为其相应的指令集: mainstream(WASM, RISC-V)EVM(EVM bytecod…...

[题]宝物筛选 #单调队列优化
五、宝物筛选(洛谷P1776) 题目链接 好家伙,找到了一个之前学习多重背包优化时的错误…… 之前记的笔记还是很有用的…… #include<bits/stdc.h> using namespace std; const int N 1e5 10; int f[N]; int n, m; int v, w, s; int l…...

.NET的键盘Hook管理类,用于禁用键盘输入和切换
一、MyHook帮助类 此类需要编写指定屏蔽的按键,灵活性差。 using System; using System.Runtime.InteropServices; using System.Diagnostics; using System.Windows.Forms; using Microsoft.Win32;namespace MyHookClass {/// <summary>/// 类一/// </su…...

Anaconda Jupyter
🙌秋名山码民的主页 😂oi退役选手,Java、大数据、单片机、IoT均有所涉猎,热爱技术,技术无罪 🎉欢迎关注🔎点赞👍收藏⭐️留言📝 获取源码,添加WX 目录 前言An…...
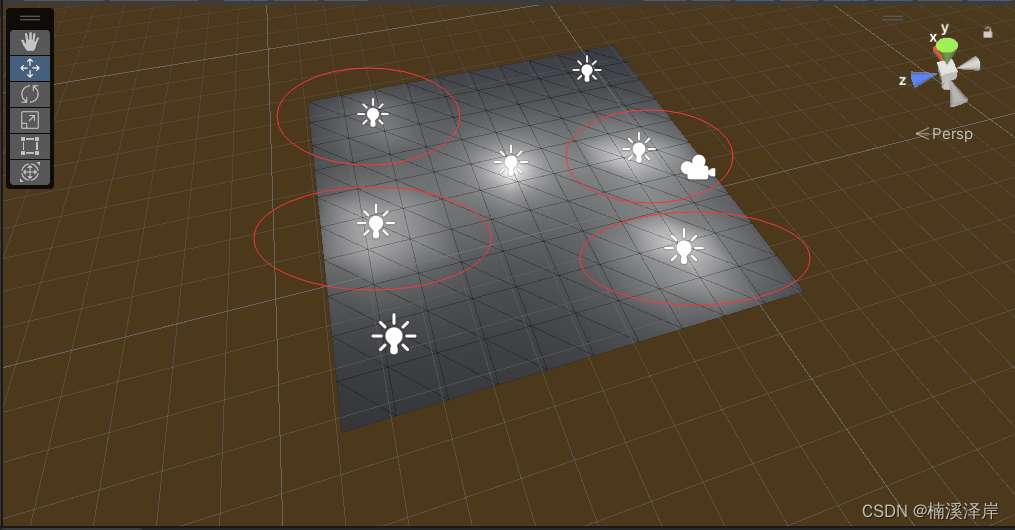
Unity中Shader的前向渲染路径ForwardRenderingPath
文章目录 前言一、前向渲染路径的特点二、渲染方式1、逐像素(效果最好)2、逐顶点(效果次之)3、SH球谐(效果最差) 三、Unity中对灯光设置 后,自动选择对应的渲染方式1、ForwardBase仅用于一个逐像素的平行灯,以及所有的逐顶点与SH2、ForwardAdd用于其他所…...

简历项目优化关键方法论-START
START方法论是非常著名的面试法则,经常被面试官使用的工具 Situation:情况、事情、项目需求是在什么情况下发生Task:任务,你负责的做的是什么Action:动作,针对这样的情况分析,你采用了什么行动方式Result:结果,在这样…...
TensorFlow学习1:使用官方模型进行图片分类
前言 人工智能以后会越来越发达,趁着现在简单学习一下。机器学习框架有很多,这里觉得学习谷歌的 TensorFlow,谷歌的技术还是很有保证的,另外TensorFlow 的中文文档真的很友好。 文档: https://tensorflow.google.cn/…...
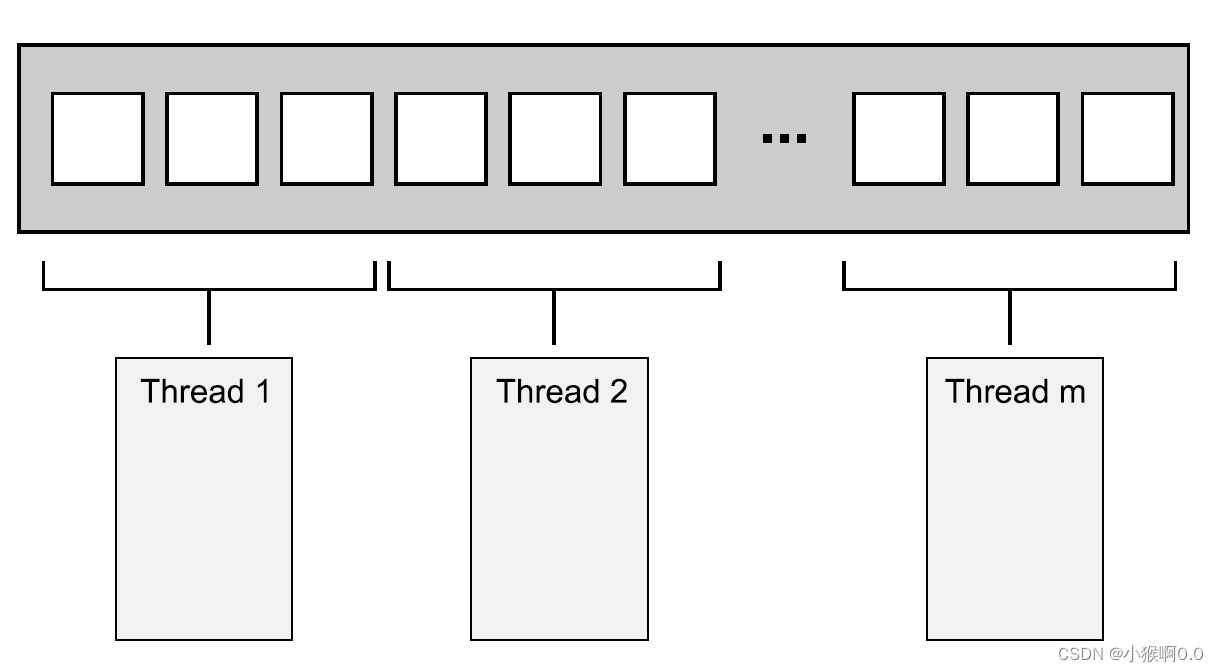
C++ 并发编程实战 第八章 设计并发代码 一
目录 8.1 在线程间切分任务 8.1.1 先在线程间切分数据,再开始处理 8.1.2 以递归方式划分数据 8.1.3 依据工作类别划分任务 借多线程分离关注点需防范两大风险 在线程间按流程划分任务 8.2 影响并发性能的因素 8.2.1 处理器的数量 8.2.2 数据竞争和缓存兵乓…...
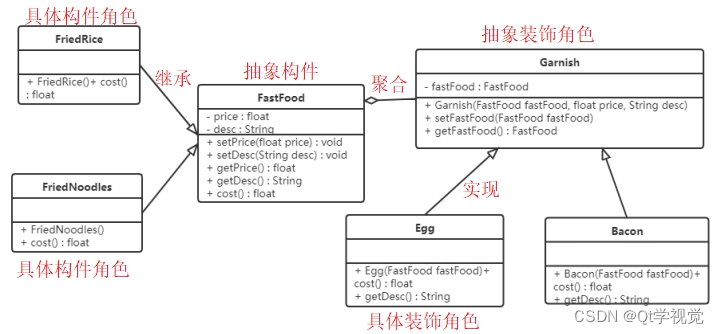
设计模式8、装饰者模式 Decorator
解释说明:动态地给一个对象增加一些额外的职责。就扩展功能而言,装饰模式提供了一种比使用子类更加灵活的替代方案 抽象构件(Component):定义一个抽象接口以规范准备收附加责任的对象 具体构件(ConcreteCom…...
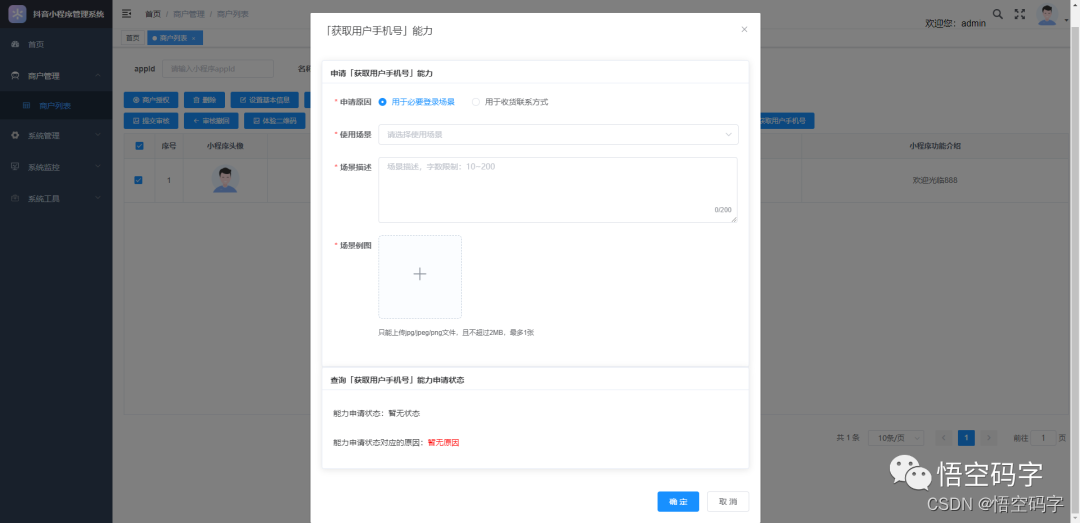
抖音开放平台第三方代小程序开发,一整套流程
大家好,我是小悟 抖音小程序第三方平台开发着力于解决抖音生态体系内的小程序管理问题,一套模板,随处部署。能尽可能地减少服务商的开发成本,服务商只用开发一套小程序代码作为模板就可以快速批量的孵化出大量的商家小程序。 第…...

Flutter笔记:滚动之-无限滚动与动态加载的实现(GetX简单状态管理版)
Flutter笔记 无限滚动与动态加载的实现(GeX简单状态管理版) 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq…...

前端架构师之02_ES6_高级
1 类和继承 1.1 class类 JavaScript 语言中,生成实例对象的传统方法是通过构造函数。 // ES5 创建对象 // 创建一个类,用户名 密码 function User(name,pass){// 添加属性this.name name;this.pass pass; } // 用 原型 添加方法 User.prototype.sho…...

VScode多文件编译/调试配置
之前都是在Visual Studio写C/C,最近想换到VScode,折腾半天把launch.json和tasks.json配好了(虽然不懂为什么,但确实能用了),在此做个记录。 参考资料:1,2,3 环境&#…...
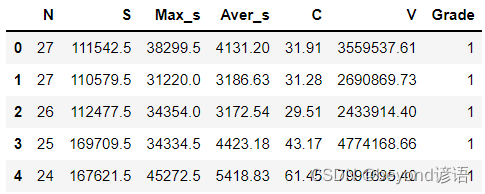
K折交叉验证——cross_val_score函数使用说明
在机器学习中,许多算法中多个超参数,超参数的取值不同会导致结果差异很大,如何确定最优的超参数?此时就需要进行交叉验证的方法,sklearn给我们提供了相应的cross_val_score函数,可对数据集进行交叉验证划分…...
2023.09.30使用golang1.18编译Hel10-Web/Databasetools的windows版
#Go 1.21新增的 log/slog 完美解决了以上问题,并且带来了很多其他很实用的特性。 本次编译不使用log/slog 包 su - echo $GOPATH ;echo $GOROOT; cd /tmp; busybox wget --no-check-certificate https://go.dev/dl/go1.18.linux-amd64.tar.gz;\ which tar&&am…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...
