数据结构与算法-(7)---栈的应用-(3)表达式转换
🌈write in front🌈
🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流.
🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如需转载还请通知⚠️
📝个人主页:Aileen_0v0🧸—CSDN博客
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏:Aileen_0v0🧸的数据结构与算法学习系列专栏🌸——CSDN博客
🗼我的格言:"没有罗马,那就自己创造罗马💫~"

目录
编辑
编辑
回顾 🧸
编辑
中缀表达式🀄
全括号表达式与前后缀表达式的关系🎡
中缀表达式转换为前后缀形式的方法🪐
通用的中缀转后缀算法⭐
利用中缀转后缀的操作流程🪂
转成后缀表达式对应的代码🚀

回顾 🧸
"温故而知新"
通过思维导图回顾一下我们学了什么,我们先学了什么是线性结构,栈(Stack)是一种抽象数据类型的线性结构,栈是什么,栈的特点以及操作步骤,我们还可以通过列表去实现栈,不过不同的栈顶其对应的时间复杂度也不同,了解完栈的基础知识点后我们开始学习栈的应用,栈可以用于
「(1)匹配符号(Balance Symbols),
(2)进制转换(Decimal conversion),
(3)表达式转换(Experssion conversion)」
(1) 和 (2) 我们已经在前面的文章写过了:不记得知识点或者对前面内容感兴趣的小伙伴可以点击👉
🔗(1)http://t.csdnimg.cn/Ypv3q
🔗(2)http://t.csdnimg.cn/OLIJW
对应专栏数据结构与算法学习系列专栏🌸🔗:http://t.csdnimg.cn/6BQDo
中缀表达式🀄
我们通常看到的表达式如:B*C , 很容易就知道是B乘以C
像 * 这种操作符( operator ) 介于操作数 ( operand )中间的表示法,称为 "中缀" 表示法.
But sometimes 中缀表示法会 case confusion(引起混淆),如 "A + B * C"
是A+B然后再乘以C 还是B*C然后再加A?
为了消除混淆,人们引入"优先级"的概念
规定高优先级的操作符先计算
相同优先级的操作符从左到右依次计算这样A+B*C就没有疑义是A加上 B与C的乘积
同时引入了括号来表示强制优先级,括号的优先级最高,而且在嵌套的括号中,内层的优先级更高这样(A+B)*C就是A与B的和再乘以C
全括号表达式与前后缀表达式的关系🎡
虽然人们已经习惯了这种表示法,但计算机处理最好是能明确规定所有的计算顺序,这样无需处理复杂的优先规则
于是,我们引入全括号表达式:
在所有的表达式项两边都加上括号A+B*C+D,应表示为((A+(B*C))+D)
可否将表达式中操作符的位置稍移动一下?
例如中缀表达式A+B将操作符移到前面,变为"+AB"
或者将操作符移到最后,变为“AB+”
我们就得到了表达式的另外两种表示法:"前缀"和“后缀”表示法以操作符相对于操作数的位置来定义
这样A+B*C将变为前缀的"+A*BC"后缀的"ABC*+"为了帮助理解,子表达式加了下划线
在前缀和后缀表达式中,操作符的次序完全决定了运算的次序,不再有混淆
所以在很多情况下,表达式在计算机中的表示都避免使用复杂的中缀形式
让我们先看看这些前中缀和后缀表达式
| 中缀表达式 | 前缀表达式 | 后缀表达式 |
| A + B * C + D | + + A * B C D | A B C * + D + |
| ( A + B ) * ( C + D ) | * + A B + C D | A B + C D + * |
| A * B + C * D | + * A B * C D | A B * C D * + |
| A + B + C + D | + + + A B C D | A B + C + D + |
想必初看的小伙伴会觉得眼花缭乱,但是不要着急,我们接下来会一一讲解.
一定得有个算法来转换任意复杂的表达式
为了分解算法的复杂度,我们从“全括号中缀表达式入手我们看A+B*C,
如果写成全括号形式:(A+(B*C)),显式表达了计算次序我们注意到每一对括号,都包舍了一组完整的操作符和操作数,让我们看看如何将其转换成前后缀表达式吧~

中缀表达式转换为前后缀形式的方法🪐
✨Summary:
(1)将中缀表达式转换为全括号形式
(2)将所有的操作符移动到子表达式所在的 左括号(前缀prefix) 或者 右括号(后缀postfix) 处~
替代之,再删除所有的括号.
通用的中缀转后缀算法⭐
在中缀表达式转换为后缀形式的处理过程中,操作符比操作数要晚输出
所以在扫描到对应的第二个操作数之前,需要把操作符先保存起来
而这些暂存的操作符,由于优先级的规则还有可能要反转次序输出.
在A+B*C中,+虽然先出现,但优先级比后面这个*要低,所以它要等*处理完后,才能再处理.
这种反转特性,使得我们考虑用栈来保存暂时未处理的操作符
再看看(A+B)*C,对应的后缀形式是AB+C*
这里+的输出比*要早,主要是因为括号使得+的优先级提升,高于括号之外的*
根据上面的“全括号”表达式,后缀表达式中操作符应该出现在左括号对应的右括号位置
所以遇到左括号,要标记下,其后出现的操作符优先级提升了,一旦扫描到对应的右括号,就可以马上输出这个操作符
总结:
在从左到右扫描逐个字符扫描中缀表达式的过程中,采用一个栈来暂存未处理的操作符
这样,栈顶的操作符就是最近暂存进去的,当遇到一个新的操作符,就需要跟栈顶的操作符比较下优先级,再行处理--->新符号和栈顶对比,新的高,就入栈(因为取时也先取); 新的低,就把栈顶出栈,让栈顶的先运算.
利用中缀转后缀的操作流程🪂
后面的算法描述中,约定中缀表达式是由空格隔开的一系列单词(token)构成,
操作符单词包括*/+-()
而操作数单词则是单字母标识符A、B、C等。
1.首先,创建空栈opstack用于暂存操作符,空表postfixList用于保存后缀表达式
2.将中缀表达式转换为单词(token)列表
A + B*C = split => ['A', '+', 'B', ' * ', 'C']


图解:
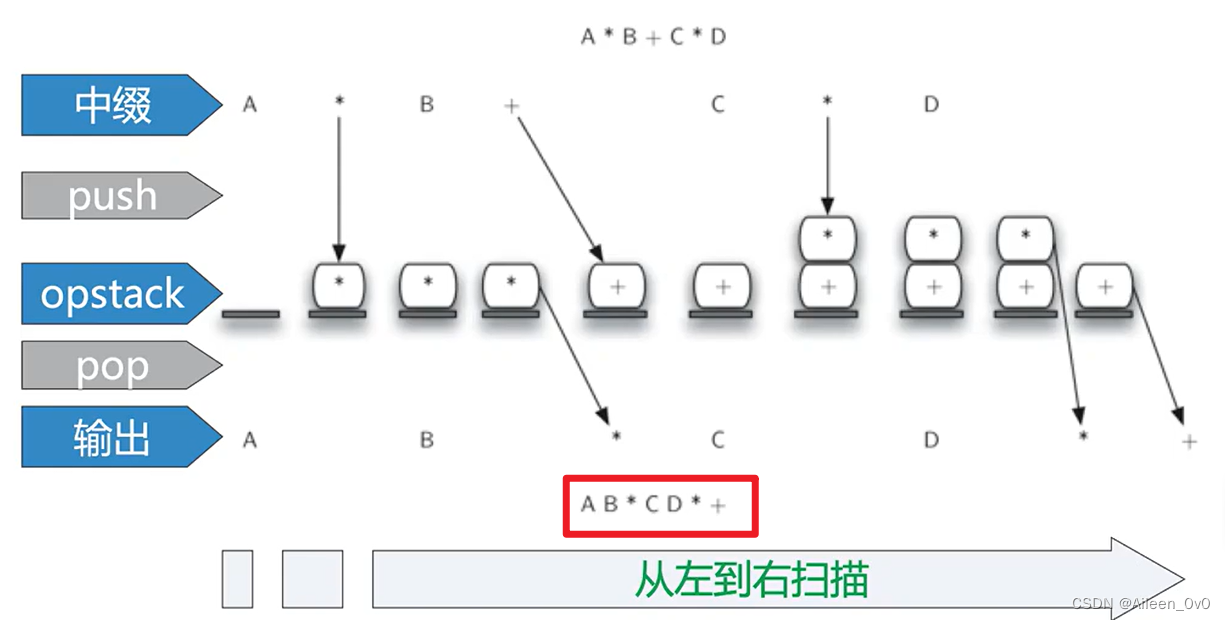
转成后缀表达式对应的代码🚀
class Stack:#Stack---->ADTdef __init__(self):self.items =[]def isEmpty(self):return self.items == []# 满足这些属性(行为)的是栈def push(self,item):self.items.append(item)def pop(self):return self.items.pop()def peek(self):return self.items[len(self.items)-1]#def size(self):return len(self.items)def infixToPostfix(infixexpr):# 记录操作符优先级prec = {}prec["*"] = 3prec["/"] = 3prec["+"] = 2prec["-"] = 2prec["("] = 1opStack = Stack()postfixList = []# 解析表达式到列表tokenList = infixexpr.split()for token in tokenList:# 操作数if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":postfixList.append(token)# (elif token == "(":opStack.push(token)# )elif token == ")":topToken = opStack.pop()while topToken != '(':postfixList.append(topToken)topToken = opStack.pop()# 操作符else:while (not opStack.isEmpty()) and \(prec[opStack.peek()] >= prec[token]):postfixList.append(opStack.pop())opStack.push(token)while not opStack.isEmpty():# 操作符postfixList.append(opStack.pop())# 合成后缀表达式字符串 return " ".join(postfixList)
print(infixToPostfix("A + B * C "))运行代码测试结果 :


相关文章:

数据结构与算法-(7)---栈的应用-(3)表达式转换
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...
)
Lilliefors正态性检验(一种非参数统计方法)
Lilliefors检验(也称为Kolmogorov-Smirnov-Lilliefors检验)是一种用于检验数据是否符合正态分布的统计检验方法,它是Kolmogorov-Smirnov检验的一种变体,专门用于小样本情况。与K-S检验不同,Lilliefors检验不需要假定数…...
)
【云原生】配置Kubernetes CronJob自动备份MySQL数据库(单机版)
文章目录 每天自动备份数据库MySQL【云原生】配置Kubernetes CronJob自动备份Clickhouse数据库 每天自动备份数据库 MySQL 引用镜像:databack/mysql-backup,使用文档:https://hub.docker.com/r/databack/mysql-backup 测试、开发环境:每天0点40分执行全库备份操作,备份文…...
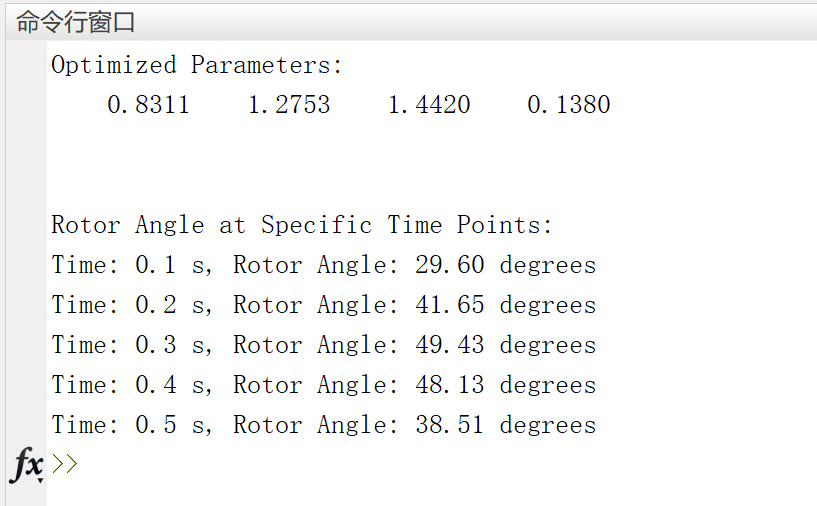
基于PSO算法的功率角摆动曲线优化研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
)
数论知识点总结(一)
文章目录 目录 文章目录 前言 一、数论有哪些 二、题法混讲 1.素数判断,质数,筛法 2.最大公约数和最小公倍数 3.快速幂 4.约数 前言 现在针对CSP-J/S组的第一题主要都是数论,换句话说,持数论之剑,可行天下矣! 一、数论有哪些 数论 原根,素数判断,质数,筛法最大公约数…...

知识分享 钡铼网关功能介绍:使用SSLTLS 加密,保证MQTT通信安全
背景 为了使不同的设备或系统能够相互通信,让旧有系统和新的系统可以集成,通信更加灵活和可靠。以及将数据从不同的来源收集并传输到不同的目的地,实现数据的集中管理和分发。 通信网关完美克服了这一难题,485或者网口的设备能通过…...

asp.net core mvc区域路由
ASP.NET Core 区域路由(Area Routing)是一种将应用程序中的路由划分为多个区域的方式,类似于 MVC 的控制器和视图的区域划分。区域路由可以帮助开发人员更好地组织应用程序的代码和路由,并使其更易于维护。 要使用区域路由&#…...
KNN(下):数据分析 | 数据挖掘 | 十大算法之一
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...

Servlet开发-session和cookie理解案例-登录页面
项目展示 进入登录页面,输入正确的用户名和密码以后会自动跳到主页 登录成功以后打印用户名以及上次登录的时间,如果浏览器和客户端都保存有上次登录的信息,则不需要登录就可以进入主页 编码思路 1.首先提供一个登录的前端页面&…...
Polygon Miden:扩展以太坊功能集的ZK-optimized rollup
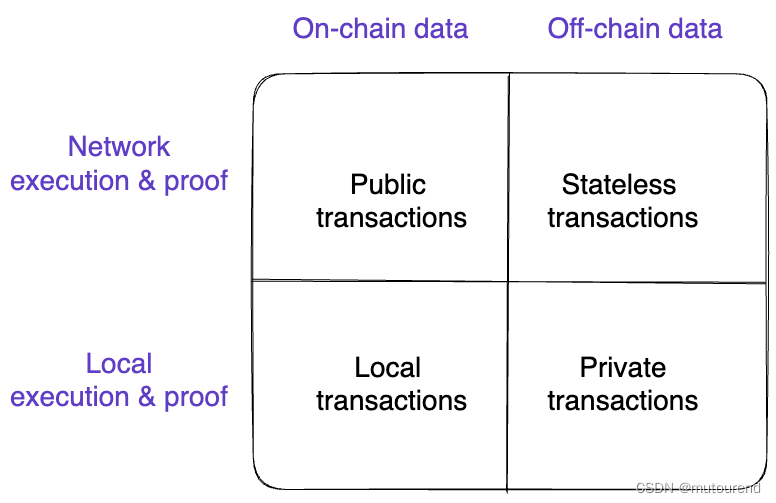
1. 引言 Polygon Miden定位为zkVM,定于2023年Q4上公开测试网。 zk、zkVM、zkEVM及其未来中指出,当前主要有3种类型的zkVM,括号内为其相应的指令集: mainstream(WASM, RISC-V)EVM(EVM bytecod…...

[题]宝物筛选 #单调队列优化
五、宝物筛选(洛谷P1776) 题目链接 好家伙,找到了一个之前学习多重背包优化时的错误…… 之前记的笔记还是很有用的…… #include<bits/stdc.h> using namespace std; const int N 1e5 10; int f[N]; int n, m; int v, w, s; int l…...

.NET的键盘Hook管理类,用于禁用键盘输入和切换
一、MyHook帮助类 此类需要编写指定屏蔽的按键,灵活性差。 using System; using System.Runtime.InteropServices; using System.Diagnostics; using System.Windows.Forms; using Microsoft.Win32;namespace MyHookClass {/// <summary>/// 类一/// </su…...

Anaconda Jupyter
🙌秋名山码民的主页 😂oi退役选手,Java、大数据、单片机、IoT均有所涉猎,热爱技术,技术无罪 🎉欢迎关注🔎点赞👍收藏⭐️留言📝 获取源码,添加WX 目录 前言An…...
Unity中Shader的前向渲染路径ForwardRenderingPath
文章目录 前言一、前向渲染路径的特点二、渲染方式1、逐像素(效果最好)2、逐顶点(效果次之)3、SH球谐(效果最差) 三、Unity中对灯光设置 后,自动选择对应的渲染方式1、ForwardBase仅用于一个逐像素的平行灯,以及所有的逐顶点与SH2、ForwardAdd用于其他所…...

简历项目优化关键方法论-START
START方法论是非常著名的面试法则,经常被面试官使用的工具 Situation:情况、事情、项目需求是在什么情况下发生Task:任务,你负责的做的是什么Action:动作,针对这样的情况分析,你采用了什么行动方式Result:结果,在这样…...
TensorFlow学习1:使用官方模型进行图片分类
前言 人工智能以后会越来越发达,趁着现在简单学习一下。机器学习框架有很多,这里觉得学习谷歌的 TensorFlow,谷歌的技术还是很有保证的,另外TensorFlow 的中文文档真的很友好。 文档: https://tensorflow.google.cn/…...
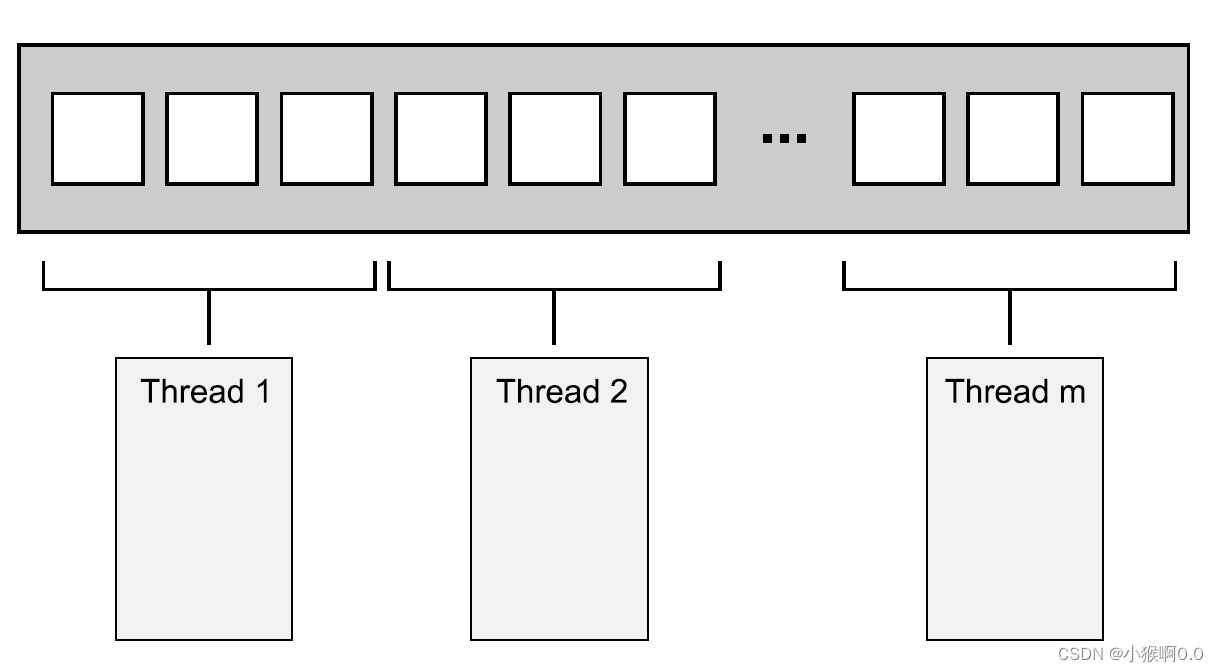
C++ 并发编程实战 第八章 设计并发代码 一
目录 8.1 在线程间切分任务 8.1.1 先在线程间切分数据,再开始处理 8.1.2 以递归方式划分数据 8.1.3 依据工作类别划分任务 借多线程分离关注点需防范两大风险 在线程间按流程划分任务 8.2 影响并发性能的因素 8.2.1 处理器的数量 8.2.2 数据竞争和缓存兵乓…...
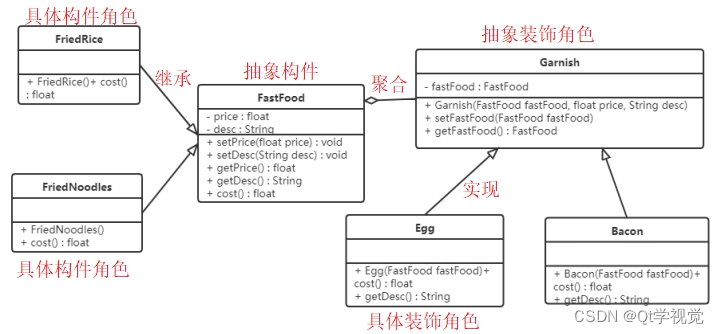
设计模式8、装饰者模式 Decorator
解释说明:动态地给一个对象增加一些额外的职责。就扩展功能而言,装饰模式提供了一种比使用子类更加灵活的替代方案 抽象构件(Component):定义一个抽象接口以规范准备收附加责任的对象 具体构件(ConcreteCom…...
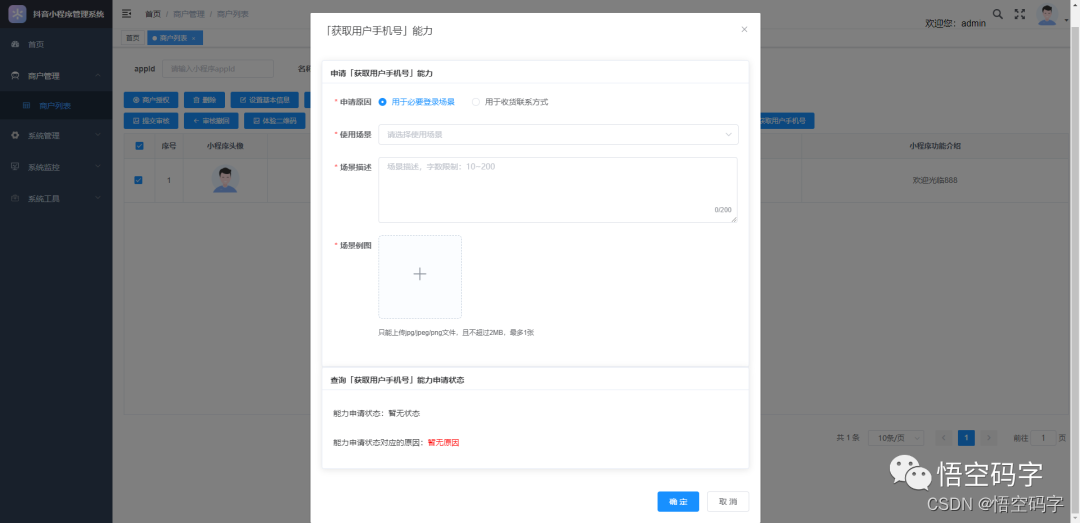
抖音开放平台第三方代小程序开发,一整套流程
大家好,我是小悟 抖音小程序第三方平台开发着力于解决抖音生态体系内的小程序管理问题,一套模板,随处部署。能尽可能地减少服务商的开发成本,服务商只用开发一套小程序代码作为模板就可以快速批量的孵化出大量的商家小程序。 第…...

Flutter笔记:滚动之-无限滚动与动态加载的实现(GetX简单状态管理版)
Flutter笔记 无限滚动与动态加载的实现(GeX简单状态管理版) 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...