刷题记录:牛客NC24309Overplanting (Silver)
传送门:牛客
题目描述:
Farmer John has purchased a new machine that is capable of planting grass within any rectangular region of
his farm that is "axially aligned" (i.e., with vertical and horizontal sides). Unfortunately, the machine
malfunctions one day and plants grass in not one, but N (1 <= N <= 1000) different rectangular regions, some
of which may even overlap.
Given the rectangular regions planted with grass, please help FJ compute the total area in his farm that is
now covered with grass.
输入:
2
0 5 4 1
2 4 6 2
输出:
20
一道扫描线的题目.但是因为数据范围比较小,所以可以使用二维差分来做
但是我既然是在线段树的题单中碰到了这道题,当然就直接用线段树做啦.毕竟用线段树来实现扫描线本身就是对二维差分做法的优化
对于扫描线算法,网上有大量博客对此进行讲解,此处就不在赘述了
为各位在提供一个有关这道题的另一种题面(不要换了题面就不会做了):
有一个数列,初始值均为0,他进行N次操作,每次将数列[ai,bi)这个区间中所有比Hi小的数改为Hi,他想知道N次操作后数列中所有元素的和。
看了这个题面有没有感觉扫描线的一些神奇之处??感觉有点积分的思想在那里了,反正我刚开始看到这道题(当我学完扫描线之后),我当时仍然是不知道怎么做的,根本就没有往扫描线那里想,还在想该怎么维护这道题.
优化&巧妙的想法:对于这种只需要区间[1,n]的维护值来说,我们建立线段树的时候可以不使用pushdown(因为我们根本不需要关注子节点是怎么样的),在子节点pushup的时候将父节点对子节点的lazy加上即可.
注意,此方法在我看来并不具有很强的意义,虽然省去了对子节点的维护,码量减少了,但是因为这种方式大大的修改了模板,会导致出现一写奇奇怪怪的错误甚至思维上的混乱,在比赛时并不建议这么做,但是在平时可以尝试一下,这样改变常规的做法可以大大增强自己对线段树的理解
下面是具体的代码部分(标准版维护版):
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define int long long
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
struct Segment_tree{int l,r,cov,lazy;
}tree[maxn*8];
struct Line{int l,r,y,cate;
}line[maxn];
bool cmp(Line A,Line B) {if(A.y==B.y) return A.l<B.l;else return A.y<B.y;
}
int n;vector<int>v;
int Getid(int x) {return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
void build(int l,int r,int rt) {tree[rt].l=l;tree[rt].r=r;if(l==r) return ;int mid=(l+r)>>1;build(lson);build(rson);
}
void pushup(int rt) {tree[rt].cov=min(tree[ls].cov,tree[rs].cov);
}
void change(int rt,int val) {tree[rt].cov+=val;tree[rt].lazy+=val;
}
void pushdown(int rt) {change(ls,tree[rt].lazy);change(rs,tree[rt].lazy);tree[rt].lazy=0;
}
void update(int l,int r,int val,int rt) {if(tree[rt].l==l&&tree[rt].r+1==r) {change(rt,val);return ;}if(tree[rt].lazy) pushdown(rt);int mid=(tree[rt].l+tree[rt].r)>>1;if(r<=mid+1) update(l,r,val,ls);else if(l>=mid+1) update(l,r,val,rs);else update(l,mid+1,val,ls),update(mid+1,r,val,rs);pushup(rt);
}
int query(int l,int r,int rt) {if(tree[rt].l==l&&tree[rt].r+1==r) {if(tree[rt].cov) return v[r-1]-v[l-1];else if(tree[rt].l==tree[rt].r) return 0; }if(tree[rt].lazy) pushdown(rt);int mid=(tree[rt].l+tree[rt].r)>>1;if(r<=mid+1) return query(l,r,ls);else if(l>=mid+1) return query(l,r,rs);else return query(l,mid+1,ls)+query(mid+1,r,rs);
}
signed main() {n=read();int cnt=0;for(int i=1;i<=n;i++) {int x1=read(),y1=read(),x2=read(),y2=read();line[++cnt].l=x1;line[cnt].r=x2;line[cnt].y=min(y1,y2);line[cnt].cate=1;line[++cnt].l=x1;line[cnt].r=x2;line[cnt].y=max(y1,y2);line[cnt].cate=-1;v.push_back(x1);v.push_back(x2);}sort(v.begin(),v.end());v.erase(unique(v.begin(),v.end()),v.end());int Size=v.size();build(1,Size,1);sort(line+1,line+2*n+1,cmp);int ans=0;int pre=0;for(int i=1;i<=2*n-1;i++) {int x=Getid(line[i].l),x2=Getid(line[i].r);update(x,x2,line[i].cate,1);ans+=query(1,Size,1)*(line[i+1].y-line[i].y);}cout<<ans<<endl;return 0;
}
下面是具体的代码部分(不维护pushdownpushdownpushdown版):
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define int long long
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
struct Segment_tree{int l,r,cov,len;
}tree[maxn*8];
struct Line{int l,r,y,cate;
}line[maxn];
bool cmp(Line A,Line B) {if(A.y==B.y) return A.l<B.l;else return A.y<B.y;
}
int n;
void build(int l,int r,int rt) {tree[rt].l=l;tree[rt].r=r;tree[rt].cov=0;tree[rt].len=0;if(l==r) return ;int mid=(l+r)>>1;build(lson);build(rson);
}
vector<int>v;
void pushup(int rt) {if(tree[rt].cov) tree[rt].len=v[tree[rt].r]-v[tree[rt].l-1];else tree[rt].len=tree[ls].len+tree[rs].len;
}
void update(int l,int r,int rt,int val) {if(tree[rt].l==l&&tree[rt].r+1==r) {tree[rt].cov+=val;if(tree[rt].cov!=0) tree[rt].len=v[r-1]-v[l-1];else pushup(rt);return ;}int mid=(tree[rt].l+tree[rt].r)>>1;if(r<=mid+1) update(l,r,ls,val);else if(l>=mid+1) update(l,r,rs,val);else update(l,mid+1,ls,val),update(mid+1,r,rs,val);pushup(rt);
}
int Getid(int x) {return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
signed main() {n=read();int cnt=0;for(int i=1;i<=n;i++) {int x1=read(),y1=read(),x2=read(),y2=read();line[++cnt].l=x1;line[cnt].r=x2;line[cnt].y=min(y1,y2);line[cnt].cate=1;line[++cnt].l=x1;line[cnt].r=x2;line[cnt].y=max(y1,y2);line[cnt].cate=-1;v.push_back(x1);v.push_back(x2);}sort(v.begin(),v.end());v.erase(unique(v.begin(),v.end()),v.end());int Size=v.size();build(1,Size,1);sort(line+1,line+2*n+1,cmp);int ans=0;int pre=0;for(int i=1;i<=2*n-1;i++) {int x=Getid(line[i].l),x2=Getid(line[i].r);update(x,x2,1,line[i].cate);ans+=tree[1].len*(line[i+1].y-line[i].y);}cout<<ans<<endl;return 0;
}
相关文章:
)
刷题记录:牛客NC24309Overplanting (Silver)
传送门:牛客 题目描述: Farmer John has purchased a new machine that is capable of planting grass within any rectangular region of his farm that is "axially aligned" (i.e., with vertical and horizontal sides). Unfortunately, the machine malfunc…...

Spring Boot中使用Sa-Token实现轻量级登录与鉴权
1. Sa-Token 介绍 Sa-Token 是一个轻量级 Java 权限认证框架,主要解决:登录认证、权限认证、单点登录、OAuth2.0、分布式Session会话、微服务网关鉴权 等一系列权限相关问题。 功能结构图 2. 登录认证 对于一些登录之后才能访问的接口(例如&…...
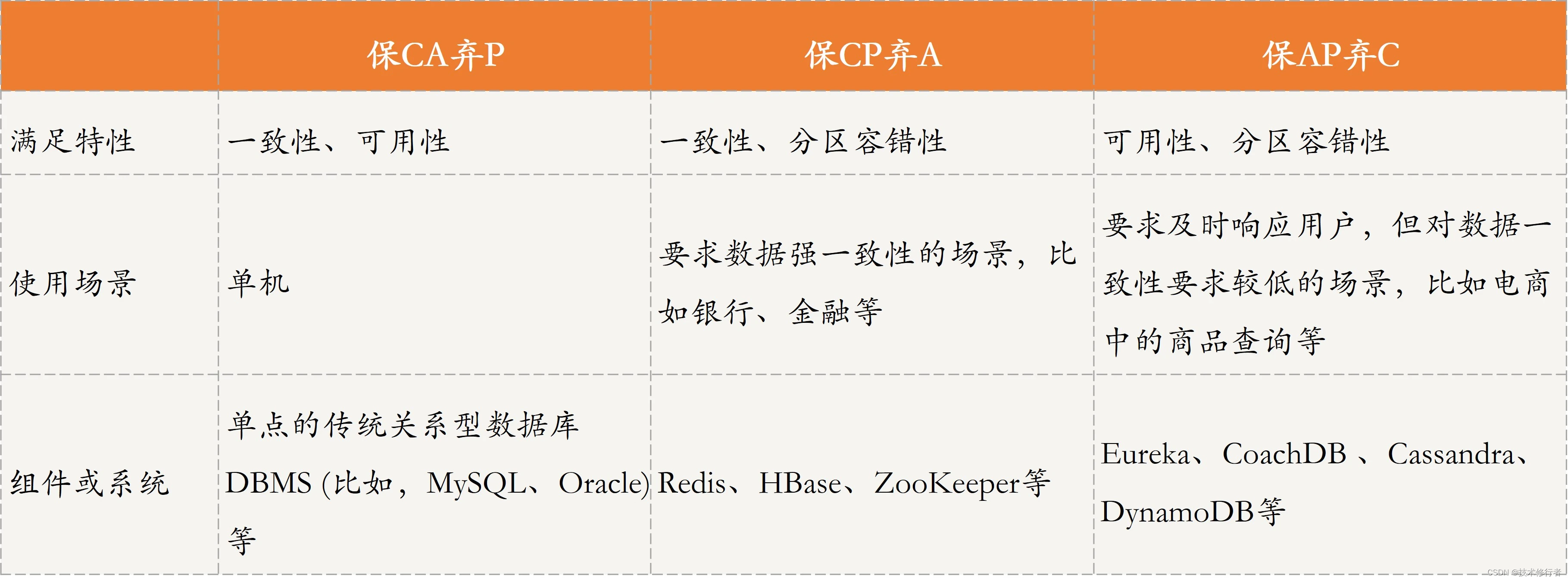
《分布式技术原理与算法解析》学习笔记Day20
CAP理论 什么是CAP理论? CAP理论用来指导分布式系统设计,以保证系统的可用性、数据一致性等。 C,Consistency,一致性,指所有节点在同一时刻的数据是相同的,即更新操作执行结束并响应用户完成后ÿ…...

【2023-2-23】FastDeploy 安装教程
【2023-2-22】FastDeploy 安装编译教程 该测试 FastDeploy CPU版本。 1. fastDeploy库编译 1.1 官方预编译库下载 预编译库下载安装 1.2 自定义CPU版本库编译 官方编译FastDeploy教程 CMakeGUI VS 2019 IDE编译FastDeploy 本人编译教程 CMAKE_CONFIGURATION_TYPES 属性设…...

rollup.js 一个简单实用的打包工具
最近在看vue3相关的知识的时候,发现了一个新的打包工具,至少于我而言是新鲜的。它就是rollup.js。一说到JS打包、合并、压缩、模块处理等都会想到webpack,这是王者,当然入门的难度偏高。而vue3中搭配的vite运行速度确实非常快&…...
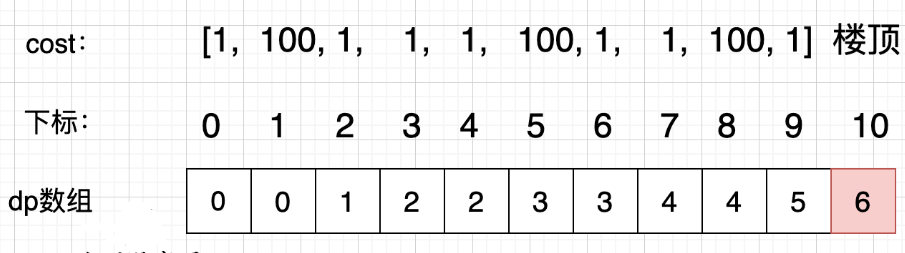
数据结构与算法之最小爬楼梯费用动态规划
继续上一道题目,在上一道题目的基础之上,我们来解决这一道爬楼梯最小费用题。一.题目描述二.思路(动态规划五部曲)确定dp数组以及下标的含义使用动态规划,就要有一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了。dp[i]的…...

阿里云ACA认证如何获取?
获取阿里云ACA(Alibaba Cloud Certification Associate)认证,需要按照以下步骤进行操作: 注册阿里云账号。如果您还没有阿里云账号,请先注册一个账号。登录阿里云官网。登录后,进入阿里云认证中心。选择AC…...
【Python入门第十六天】Python If ... Else
Python 条件和 If 语句 Python 支持来自数学的常用逻辑条件: 等于:a b不等于:a ! b小于:a < b小于等于:a < b大于:a > b大于等于:a > b 这些条件能够以多种方式使用,…...

两数之和的解法
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。你可以按任意顺序返回答案…...
领导催我优化SQL语句,我求助了ChatGPT。这是ChatGPT给出的建议,你们觉得靠谱吗
作为一个程序员,无论在面试还是工作中,优化SQL都是绕不过去的难题。 为啥?工作之后才会明白,随着公司的业务量增多,SQL的执行效率对程系统运行效率的影响逐渐增大,相对于改造代码,优化SQL语句是…...
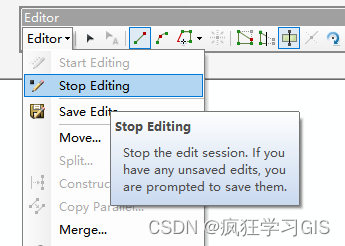
ArcGIS手动分割矢量面要素从而划分为多个面部分的方式:Cut Polygons Tool
本文介绍在ArcGIS下属ArcMap软件中,通过“Cut Polygons Tool”工具,对一个面要素矢量图层加以手动分割,从而将其划分为指定形状的多个部分的方法。 对于一个面要素矢量文件,有时我们需要对其加以划分,通过手动勾勒新的…...

【LeetCode】剑指 Offer 13. 机器人的运动范围 p92 -- Java Version
题目链接:https://leetcode.cn/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/ 1. 题目介绍(13. 机器人的运动范围) 地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动࿰…...

[oeasy]python0091_仙童公司_八叛逆_intel_8080_altair8800_牛郎星
编码进化 个人电脑 计算机 通过电话网络 进行连接 极客 利用技术 做一些有趣的尝试 极客文化 是 认真研究技术的 文化 计算机 不再是 高校和研究机构高墙里面的 神秘事物而是 生活中常见的 家用电器 ibm 蓝色巨人脚步沉重 dec 小型机不断蚕食低端市场甚至组成网络干掉大型机…...

crontab 执行脚本报错,手动执行脚本正常的解决方法
一、出现的问题 有一个守护脚本XXX.sh,需要使用oracle用户在linux上配置定时任务,每1分钟检查执行一次。但是发现该脚本使用oralce用户手动启动没问题,能正常把程序启动起来,而使用crontab并没有把程序启动起来。 二、排查分析问…...

扎心话题 | 设计院背后的潜规则你知道吗?
大家好,我是建模助手。 大家都知道,在过去的2022年经济是真难!以小编所在的广东为例,全年GDP增长仅1.9%。 这个数据足以呈现一个社会现象——不仅消费力咔咔下降,各行各业更有不同程度地嗝屁。这其中也包括一些设计院…...

【JavaEE初阶】第二节.多线程( 进阶篇 ) 锁的优化、JUC的常用类、线程安全的集合类
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、synchronized的优化操作 1.1 锁膨胀/锁升级 1.2 锁消除 1.3 锁粗化二、JUC 2.1 Callable接口 2.2 ReentrantLock类&…...

大数据核心技术是什么
大数据的核心层:数据采集层、数据存储与分析层、数据共享层、数据应用层,可能叫法有所不同本质上的角色都大同小异。 大数据的核心技术都包括什么? 1、数据采集 数据采集的任务就是把数据从各种数据源中采集和存储到数据存储上,…...

「TCG 规范解读」初识 TPM 2.0 库续一
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...

task与function
task和function主要是有助于代码的可重用性,都可以在module-endmodule之外声明。 1.function 1.1.function逻辑的综合 function:一个只有1个wire型输出值、全是组合逻辑的函数,且函数名即输出信号名,小括号中按顺序例化输入信号。…...
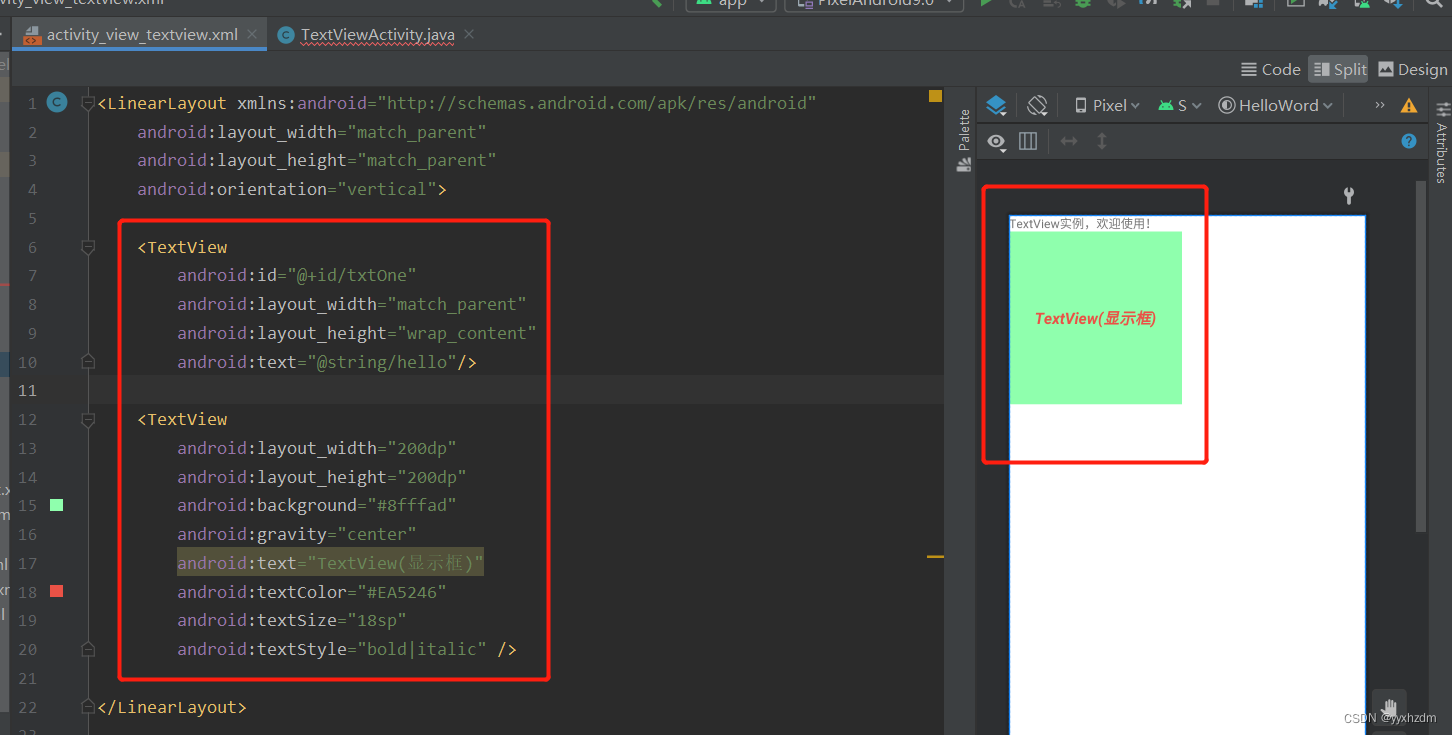
Android 基础知识4-3.1 TextView(文本框)详解
一、前言 TextView就是一个显示文本标签的控件,就是用来显示文本。可以在代码或者 XML中设置字体,字体大小,字体颜色 ,字体样式 (加粗级斜体),文字截断(比如:只显示10个字…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
