力扣第150题 逆波兰表达式求值 stack c++
题目
150. 逆波兰表达式求值
中等
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为
'+'、'-'、'*'和'/'。 - 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
示例 1:
输入:tokens = ["2","1","+","3","*"] 输出:9 解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = ["4","13","5","/","+"] 输出:6 解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"] 输出:22 解释:该算式转化为常见的中缀算术表达式为:((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = ((10 * (6 / (12 * -11))) + 17) + 5 = ((10 * (6 / -132)) + 17) + 5 = ((10 * 0) + 17) + 5 = (0 + 17) + 5 = 17 + 5 = 22
提示:
1 <= tokens.length <= 104tokens[i]是一个算符("+"、"-"、"*"或"/"),或是在范围[-200, 200]内的一个整数
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
- 平常使用的算式则是一种中缀表达式,如
( 1 + 2 ) * ( 3 + 4 )。 - 该算式的逆波兰表达式写法为
( ( 1 2 + ) ( 3 4 + ) * )。
逆波兰表达式主要有以下两个优点:
- 去掉括号后表达式无歧义,上式即便写成
1 2 + 3 4 + *也可以依据次序计算出正确结果。 - 适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中
思路和解题方法
首先,我们创建一个栈
stk用于存储数字。然后遍历字符串数组tokens中的每一个元素。如果当前元素是数字,我们将其转换为整数并将其压入栈
stk中。如果当前元素是操作符,我们从栈
stk中弹出两个元素进行计算,并将计算结果压入栈stk中。最后,栈顶元素即为逆波兰表达式的计算结果,将其返回即可。
在实现过程中,我们使用一个辅助函数
isNumber(),通过判断当前元素是否为运算符来确定相应的操作。
复杂度
时间复杂度:
O(n)
空间复杂度均为 O(n),其中 n 是字符串数组
tokens的长度。
空间复杂度
O(n)
空间复杂度为 O(n)。
c++ 代码
class Solution {
public:int evalRPN(vector<string>& tokens) {stack<int> stk; // 创建一个栈用于存储数字int n = tokens.size(); // 获取字符串数组的长度for (int i = 0; i < n; i++) { // 遍历字符串数组中的每一个元素string& token = tokens[i];if (isNumber(token)) { // 如果当前元素是数字stk.push(atoi(token.c_str())); // 将其转换为整数并压入栈中} else { // 如果当前元素是操作符int num2 = stk.top(); // 从栈中弹出第二个数字stk.pop();int num1 = stk.top(); // 从栈中弹出第一个数字stk.pop();switch (token[0]) { // 根据操作符进行计算并将结果压入栈中case '+':stk.push(num1 + num2);break;case '-':stk.push(num1 - num2);break;case '*':stk.push(num1 * num2);break;case '/':stk.push(num1 / num2);break;}}}return stk.top(); // 返回栈顶元素作为逆波兰表达式的计算结果}bool isNumber(string& token) { // 判断当前元素是否是数字return !(token == "+" || token == "-" || token == "*" || token == "/");}
};
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
相关文章:

力扣第150题 逆波兰表达式求值 stack c++
题目 150. 逆波兰表达式求值 中等 给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。 请你计算该表达式。返回一个表示表达式值的整数。 注意: 有效的算符为 、-、* 和 / 。每个操作数(运算对象)都…...
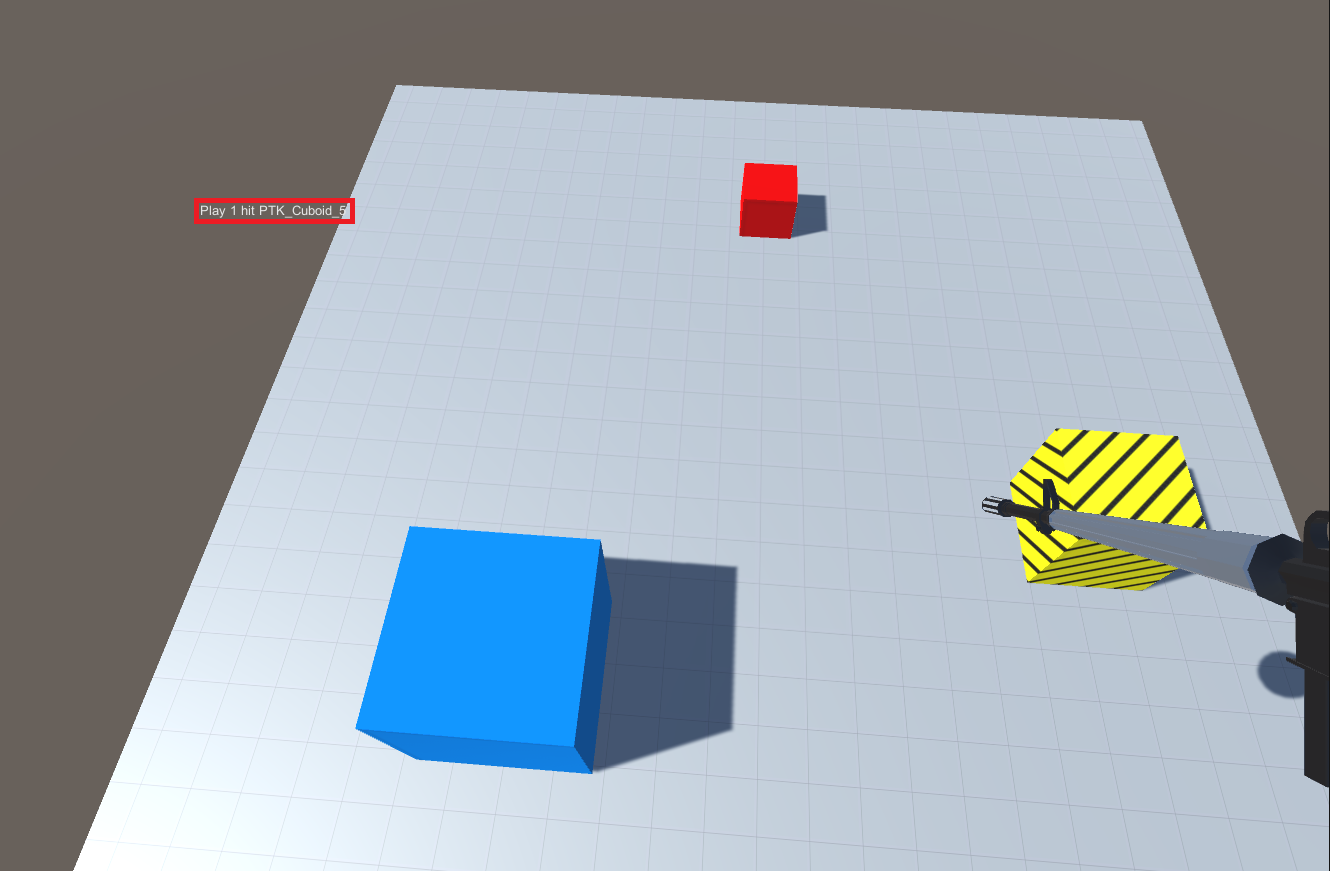
三、飞行和射击
目录 1.飞行的实现 2.限制玩家视角 3.射击的实现 4.附录 1.飞行的实现 (1)在Player预制体上挂载Configuration Joint组件,并修改其Y Drive属性 (2) 修改PlayerInput.cs和PlayerController.cs以实现飞行 PlayerIn…...
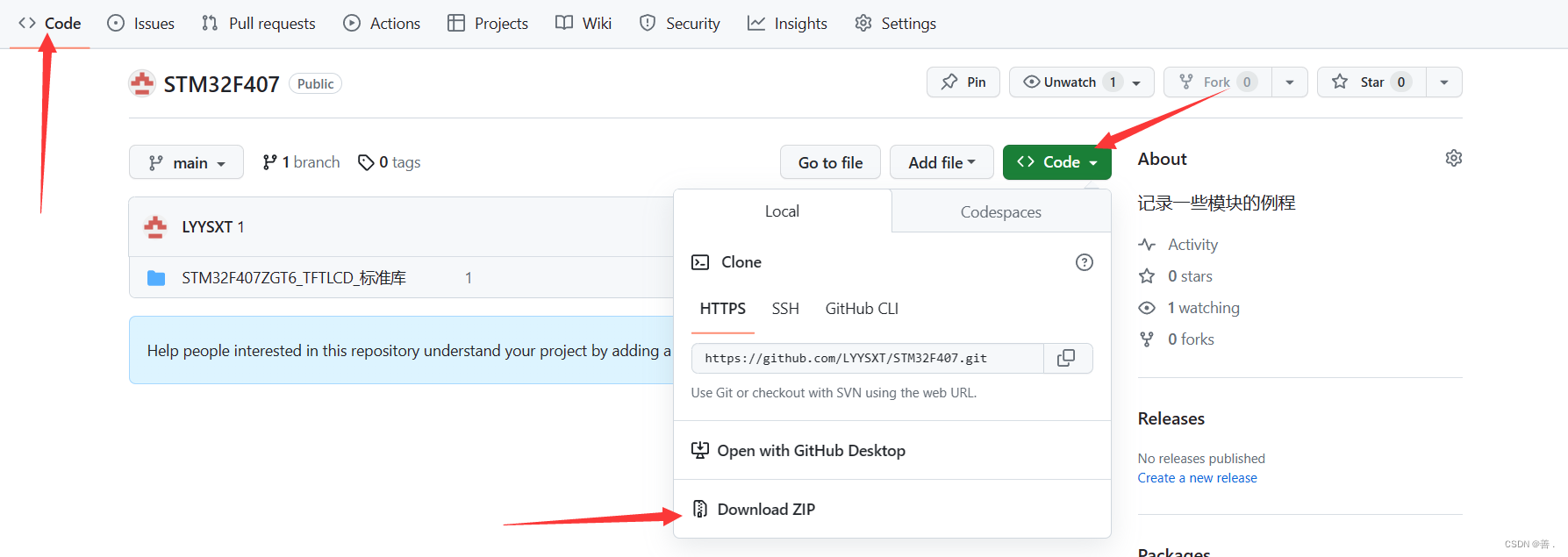
GitHub与GitHubDesktop的使用
1、介绍 见天来学习使用GitHub与GitHubDesktop。 学习前先来介绍一下什么是GitHub。 GitHub是一个基于Git的代码托管平台和开发者社区。它提供了一个Web界面,让开发者能够轻松地托管、共享和管理他们的软件项目。 在GitHub上,开发者可以创建自己的代…...

AIGC 微调的方法
AIGC 的微调方法可以分为以下步骤: 数据准备:收集尽可能多的数据,包括输入和输出数据,并将其划分为训练集、验证集和测试集。 模型选择:选择合适的模型结构,例如多层感知器(MLP)、卷…...

gcc编译webrtc x64
gcc使用Ubuntu系统已经有的gcc version 7.5.0 (Ubuntu 7.5.0-3ubuntu1~18.04) 1、下载离线版webrtc(也可以翻墙下载webrtc) 百度云链接: 链接: https://pan.baidu.com/s/1oHVz9bxXlW3Q6uO996c5XA 提取码: ojbs 2、下载gn https://github.com/timnieder…...

uni-app 实现凸起的 tabbar 底部导航栏
效果图 在 pages.json 中设置隐藏自带的 tabbar 导航栏 "custom": true, // 开启自定义tabBar(不填每次原来的tabbar在重新加载时都回闪现) 新建一个 custom-tabbar.vue 自定义组件页面 custom-tabbar.vue <!-- 自定义底部导航栏 --> <template><v…...
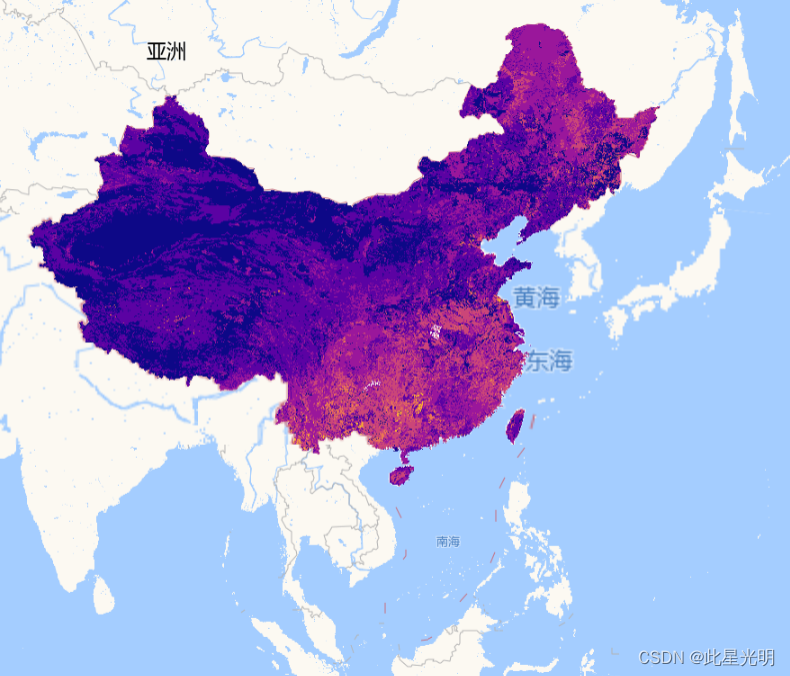
中国1km土壤特征数据集(2010年)
简介: 中国1km土壤特征数据集(2010)是基于第二次全国土壤调查的中国1:1000000比例尺土壤图和8595个土壤剖面图,以及美国农业部(USDA)中国区域土地和气候模拟标准,开发了一个多层土壤粒度分布数…...

计算机网络笔记 第二章 物理层
2.1 物理层概述 物理层要实现的功能 物理层接口特性 机械特性 形状和尺寸引脚数目和排列固定和锁定装置 电气特性 信号电压的范围阻抗匹配的情况传输速率距离限制 功能特性 -规定接口电缆的各条信号线的作用 过程特性 规定在信号线上传输比特流的一组操作过程࿰…...
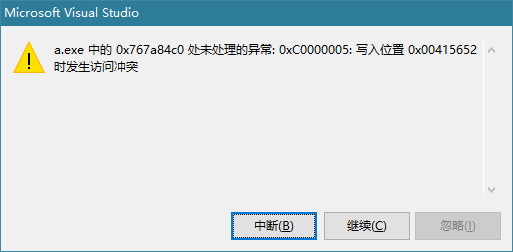
使用CreateProcess崩溃:处未处理的异常: 0xC0000005: 写入位置 0x00415652 时发生访问冲突
问题代码 if (!CreateProcess(NULL,L"pela.exe",NULL,NULL,TRUE,NULL,NULL,NULL,&si,&pi)){return 0;}如果CreateProcess的第二个参数字符串是常量或者是储存在堆中的就会被写保护,崩溃。如果字符串定义到栈或者全局变量就不存在此问题了。 正确的…...

Java 华为真题-出租车计费
需求 程序员小明打了一辆出租车去上班。出于职业敏感,他注意到这辆出租车的计费表有点问题,总是偏大。 出租车司机解释说他不喜欢数字4,所以改装了计费表,任何数字位置遇到数字4就直接跳过,其余功能都正常。 比如&…...
开源layui前端框架 收款码生成系统源码 多合一收款码生成源码 带50多套UI模板
Layui前端的多合一收款码在线生成系统源码_附多套前端UI模板。 卡特三合一收款码生成系统源码,和收款啦采用一样的原理。 内部多达50多套模板,前端跟付款界面都特别好看。 识别收款码之后会自动加密,非常安全。 一样没有后台,一样…...

微服务moleculer01
1.官网地址: Moleculer - Progressive microservices framework for Node.js 2. github代码地址: GitHub - moleculerjs/moleculer: :rocket: Progressive microservices framework for Node.js Moleculer是基于Node.js的一款快速、多功能的微服务框…...

C++中将指针传递给函数
C中将指针传递给函数 指针是一种将内存空间传递给函数的有效方式,其中可包含函数完成其工作所需的数据,也可包含操作结果。将指针作为函数参数时,确保函数只能修改您希望它修改的参数很重要。例如,如果函数根据以指针方式传入的半…...
【51单片机编写占空比按秒渐亮与渐暗】2023-10-2
昨天刚在W10上安装CH340驱动,又下载到板子上LCD1602定时器时钟程序,为了调试,调用了一个LED观察控制蜂鸣器按秒响的变量,几经调试才发觉该开发板用的是有源蜂鸣器,不用IO取反操作,直接控制IO的高低电平即可…...
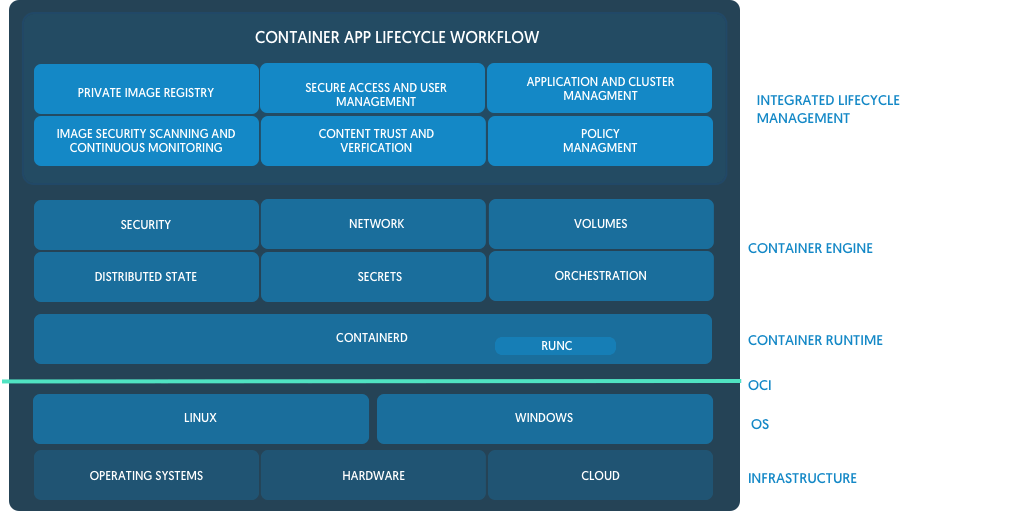
OCI 发布了容器运行时和镜像规范!
7 月 19 日是开放容器计划Open Container Initiative(OCI)的一个重要里程碑,OCI 发布了容器运行时和镜像规范的 1.0 版本,而 Docker 在这过去两年中一直充当着推动和引领的核心角色。 我们的目标是为社区、客户以及更广泛的容器行…...

C++学习笔记一: 变量和基本类型
本章讲解C内置的数据类型(如:字符、整型、浮点数等)和自定义数据类型的机制。下一章讲解C标准库里面定义的更加复杂的数据类型,比如可变长字符串和向量等。 1.基本内置类型 C内置的基本类型包括:算术类型和空类型。算…...

探索ClickHouse——同时支持导入导出功能的文件格式
在《探索ClickHouse——安装和测试》中,我们使用clickhouse直接从文件中读取数据。clickhouse支持多种格式文件的导入导出,本节我们对此进行分类介绍。 按常见格式区分 JSON 原始的JSON格式只支持导入,不支持导入。同时支持导入和导出的是…...

Scipy库提供了多种正态性检验和假设检验方法
Scipy库提供了多种正态性检验和假设检验方法。以下是一些常用的检验方法的列表: 正态性检验方法: Shapiro-Wilk检验:scipy.stats.shapiroAnderson-Darling检验:scipy.stats.andersonKolmogorov-Smirnov检验:scipy.st…...
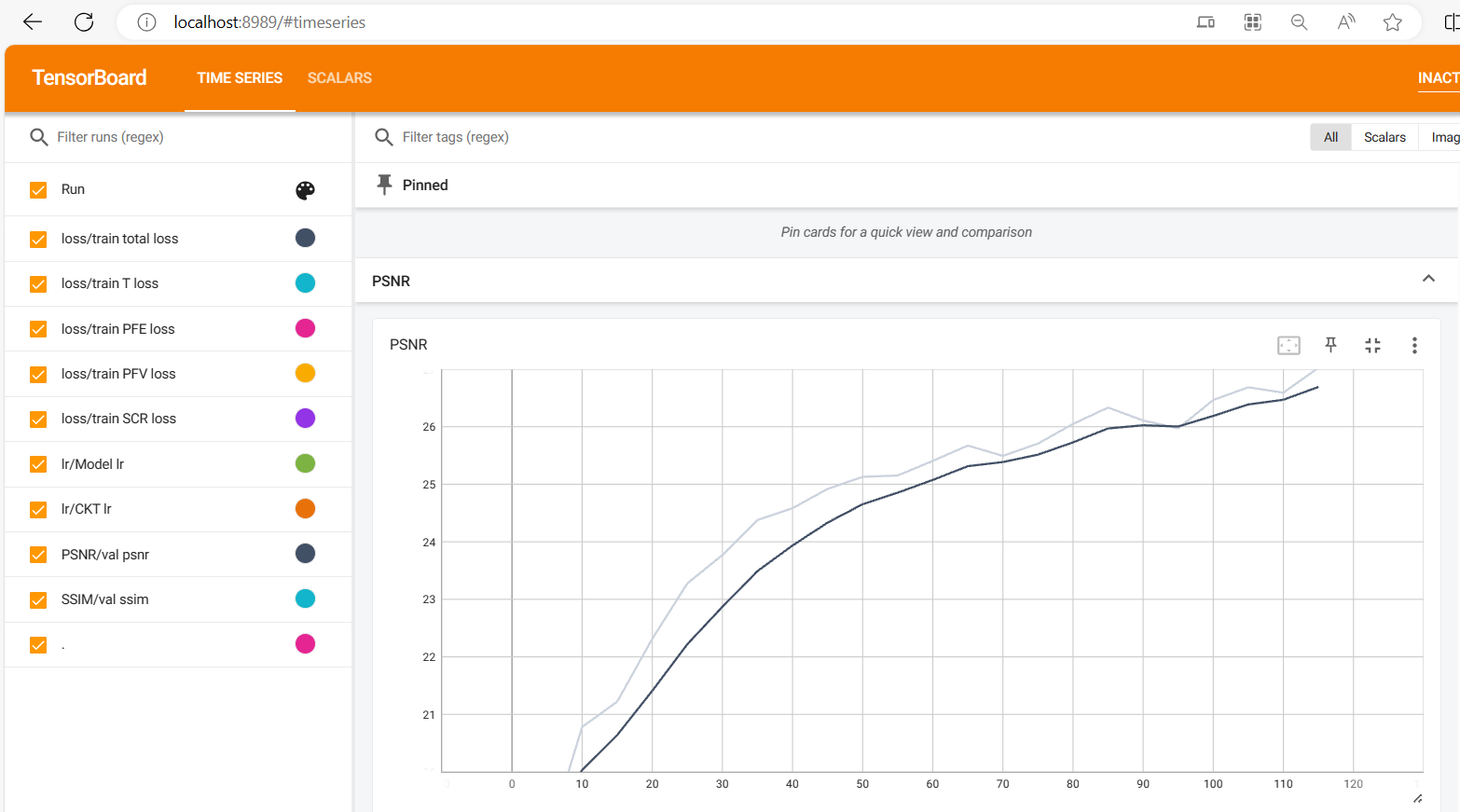
去雨去雪去雾算法之本地与服务器的TensorBoard使用教程
在进行去雨去雾去雪算法实验时,需要注意几个参数设置,num_workers只能设置为0,否则会报各种稀奇古怪的错误。 本地使用TensorBoard 此外,发现生成的文件是events.out.tfevents格式的,查询了一番得知该文件是通过Tens…...
【小沐学前端】Node.js实现基于Protobuf协议的WebSocket通信
文章目录 1、简介1.1 Node1.2 WebSocket1.3 Protobuf 2、安装2.1 Node2.2 WebSocket2.2.1 nodejs-websocket2.2.2 ws 2.3 Protobuf 3、代码测试3.1 例子1:websocket(html)3.1.1 客户端:yxy_wsclient1.html3.1.2 客户端:…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
