Scipy库提供了多种正态性检验和假设检验方法
Scipy库提供了多种正态性检验和假设检验方法。以下是一些常用的检验方法的列表:
正态性检验方法:
- Shapiro-Wilk检验:
scipy.stats.shapiro - Anderson-Darling检验:
scipy.stats.anderson - Kolmogorov-Smirnov检验:
scipy.stats.kstest - D'Agostino-Pearson检验:
scipy.stats.normaltest - Lilliefors检验:
scipy.stats.lilliefors
假设检验方法:
- 独立样本t检验:
scipy.stats.ttest_ind - 配对样本t检验:
scipy.stats.ttest_rel - 单样本t检验:
scipy.stats.ttest_1samp - 方差分析 (ANOVA):
scipy.stats.f_oneway - Kruskal-Wallis检验:
scipy.stats.kruskal - Mann-Whitney U检验:
scipy.stats.mannwhitneyu - Wilcoxon符号秩检验:
scipy.stats.wilcoxon - 卡方检验:
scipy.stats.chisquare - Fisher精确检验:
scipy.stats.fisher_exact
这些方法涵盖了在统计分析中经常用到的正态性检验和假设检验技术。你可以根据你的具体数据和研究问题选择适当的方法来进行分析。每个方法都有不同的假设和前提条件,所以在使用时需要谨慎考虑。
下面是关于这些不同正态性检验方法的简要说明:
-
Shapiro-Wilk检验(
scipy.stats.shapiro):- Shapiro-Wilk检验是一种用于检验数据是否来自正态分布的统计检验方法。
- 零假设(H0):数据来自正态分布。
- 备择假设(H1):数据不来自正态分布。
- 结果解释:如果p-value小于选择的显著性水平(通常为0.05),则拒绝零假设,表示数据不服从正态分布。
from scipy import stats import numpy as np# 创建一个示例数据集 data = np.random.normal(0, 1, 100)# 执行Shapiro-Wilk正态性检验 stat, p = stats.shapiro(data)# 输出检验结果 if p < 0.05:print("数据不服从正态分布") else:print("数据可能服从正态分布")
-
Anderson-Darling检验(
scipy.stats.anderson):- Anderson-Darling检验也用于检验数据是否来自正态分布。
- 检验的结果基于Anderson-Darling统计量和临界值。
- 结果解释:如果Anderson-Darling统计量大于临界值,则拒绝零假设,表示数据不服从正态分布。
from scipy import stats import numpy as np# 创建一个示例数据集 data = np.random.normal(0, 1, 100)# 执行Anderson-Darling正态性检验 result = stats.anderson(data)# 输出检验结果 print("Anderson-Darling统计量:", result.statistic) print("临界值:", result.critical_values) if result.statistic > result.critical_values[2]:print("数据不服从正态分布") else:print("数据可能服从正态分布")
-
Kolmogorov-Smirnov检验(
scipy.stats.kstest):- Kolmogorov-Smirnov检验用于检验数据是否来自特定的概率分布,包括正态分布。
- 检验的结果基于累积分布函数的比较。
- 结果解释:如果p-value小于选择的显著性水平,则拒绝零假设,表示数据不来自指定的分布。
from scipy import stats import numpy as np# 创建一个示例数据集 data = np.random.normal(0, 1, 100)# 执行Kolmogorov-Smirnov正态性检验 stat, p = stats.kstest(data, 'norm')# 输出检验结果 if p < 0.05:print("数据不服从正态分布") else:print("数据可能服从正态分布")
-
D'Agostino-Pearson检验(
scipy.stats.normaltest):- D'Agostino-Pearson检验也用于检验数据是否来自正态分布。
- 检验的结果基于偏度(skewness)和峰度(kurtosis)的值。
- 结果解释:如果p-value小于选择的显著性水平,则拒绝零假设,表示数据不服从正态分布。
from scipy import stats import numpy as np# 创建一个示例数据集 data = np.random.normal(0, 1, 100)# 执行D'Agostino-Pearson正态性检验 stat, p = stats.normaltest(data)# 输出检验结果 if p < 0.05:print("数据不服从正态分布") else:print("数据可能服从正态分布")
-
Lilliefors检验(
scipy.stats.lilliefors):- Lilliefors检验是一种用于检验数据是否来自特定分布的检验方法,通常用于检验是否来自正态分布。
- 结果解释:如果p-value小于选择的显著性水平,则拒绝零假设,表示数据不来自指定的分布。
from scipy import stats import numpy as np# 创建一个示例数据集 data = np.random.normal(0, 1, 100)# 执行Lilliefors正态性检验 stat, p = stats.lilliefors(data)# 输出检验结果 if p < 0.05:print("数据不服从正态分布") else:print("数据可能服从正态分布")
这些检验方法可根据你的需求选择,但需要注意,结果的解释可能会受到样本大小、数据分布和显著性水平的影响。要正确使用这些方法,通常需要深入了解它们的原理和假设。
----------------------------
假设检验方法:
这里是对这些假设检验方法的简要介绍以及它们的具体使用场合:
-
配对样本t检验(
scipy.stats.ttest_rel):- 使用场合:用于比较两组相关(配对)样本之间的均值差异,例如在同一组人群中的前后两次测量。
- 假设:检验两组相关样本的均值是否存在显著差异。
-
单样本t检验(
scipy.stats.ttest_1samp):- 使用场合:用于检验一个样本的均值是否与一个已知的参考值(或理论均值)存在显著差异。
- 假设:检验单个样本的均值是否与给定的理论均值不同。
-
方差分析 (ANOVA)(
scipy.stats.f_oneway):- 使用场合:用于比较三个或更多组样本之间的均值差异,通常用于分析不同组别之间的统计显著性。
- 假设:检验多组样本的均值是否存在显著差异。
-
Kruskal-Wallis检验(
scipy.stats.kruskal):- 使用场合:用于比较三个或更多组独立样本之间的分布差异,通常用于非正态分布的数据。
- 假设:检验多组独立样本的分布是否存在显著差异。
-
Mann-Whitney U检验(
scipy.stats.mannwhitneyu):- 使用场合:用于比较两组独立样本之间的中位数差异,通常用于非正态分布的数据。
- 假设:检验两组独立样本的中位数是否存在显著差异。
-
Wilcoxon符号秩检验(
scipy.stats.wilcoxon):- 使用场合:用于比较两组配对样本之间的中位数差异,通常用于非正态分布的配对数据。
- 假设:检验两组配对样本的中位数是否存在显著差异。
-
卡方检验(
scipy.stats.chisquare):- 使用场合:用于比较观察频数和期望频数之间的差异,通常用于分析分类数据的拟合度。
- 假设:检验观察频数与期望频数是否存在显著差异。
-
Fisher精确检验(
scipy.stats.fisher_exact):- 使用场合:用于比较两个分类变量之间的关联性,通常用于小样本数据。
- 假设:检验两个分类变量是否存在关联性。
这些检验方法适用于不同类型的数据和研究问题,你可以根据数据性质和研究目的选择合适的方法来进行统计分析。
- 独立样本t检验:
scipy.stats.ttest_indfrom scipy import stats import numpy as np# 创建两组示例数据 group1 = np.array([25, 30, 35, 40, 45]) group2 = np.array([20, 28, 32, 38, 42])# 执行独立样本t检验 t_stat, p_value = stats.ttest_ind(group1, group2)# 输出检验结果 if p_value < 0.05:print("两组数据均值存在显著差异") else:print("两组数据均值无显著差异") - 配对样本t检验:
scipy.stats.ttest_relfrom scipy import stats import numpy as np# 创建两组示例数据 before = np.array([30, 32, 34, 36, 38]) after = np.array([28, 31, 35, 37, 40])# 执行配对样本t检验 t_stat, p_value = stats.ttest_rel(before, after)# 输出检验结果 if p_value < 0.05:print("配对样本存在显著差异") else:print("配对样本无显著差异") - 单样本t检验:
scipy.stats.ttest_1sampfrom scipy import stats import numpy as np# 创建一个示例数据集 data = np.random.normal(0, 1, 100)# 执行单样本t检验 t_stat, p_value = stats.ttest_1samp(data, 0)# 输出检验结果 if p_value < 0.05:print("样本均值与零存在显著差异") else:print("样本均值与零无显著差异") - 方差分析 (ANOVA):
scipy.stats.f_onewayfrom scipy import stats import numpy as np# 创建多组示例数据 group1 = np.random.normal(0, 1, 100) group2 = np.random.normal(1, 1, 100) group3 = np.random.normal(2, 1, 100)# 执行方差分析 f_stat, p_value = stats.f_oneway(group1, group2, group3)# 输出检验结果 if p_value < 0.05:print("组之间存在显著差异") else:print("组之间无显著差异") - Kruskal-Wallis检验:
scipy.stats.kruskalfrom scipy import stats# 创建多组示例数据 group1 = [25, 30, 35, 40, 45] group2 = [20, 28, 32, 38, 42] group3 = [15, 18, 22, 28, 32]# 执行Kruskal-Wallis检验 h_stat, p_value = stats.kruskal(group1, group2, group3)# 输出检验结果 if p_value < 0.05:print("组之间存在显著差异") else:print("组之间无显著差异") - Mann-Whitney U检验:
scipy.stats.mannwhitneyufrom scipy import stats# 创建两组示例数据 group1 = [25, 30, 35, 40, 45] group2 = [20, 28, 32, 38, 42]# 执行Mann-Whitney U检验 u_stat, p_value = stats.mannwhitneyu(group1, group2)# 输出检验结果 if p_value < 0.05:print("两组数据存在显著差异") else:print("两组数据无显著差异") - Wilcoxon符号秩检验:
scipy.stats.wilcoxonfrom scipy import stats# 创建两组配对数据 before = [25, 30, 35, 40, 45] after = [20, 28, 32, 38, 42]# 执行Wilcoxon符号秩检验 w_stat, p_value = stats.wilcoxon(before, after)# 输出检验结果 if p_value < 0.05:print("配对数据存在显著差异") else:print("配对数据无显著差异") - 卡方检验:
scipy.stats.chisquarefrom scipy import stats import numpy as np# 创建一个示例观察频数数组 observed = np.array([20, 25, 30]) expected = np.array([15, 30, 30])# 执行卡方检验 chi_stat, p_value = stats.chisquare(observed, f_exp=expected)# 输出检验结果 if p_value < 0.05:print("观察频数与期望频数存在显著差异") else:print("观察频数与期望频数无显著差异") - Fisher精确检验:
scipy.stats.fisher_exactfrom scipy import stats# 创建一个2x2的列联表 contingency_table = [[10, 5], [3, 15]]# 执行Fisher精确检验 odds_ratio, p_value = stats.fisher_exact(contingency_table)# 输出检验结果 if p_value < 0.05:print("两个分类变量存在关联") else:print("两个分类变量无关联")
相关文章:

Scipy库提供了多种正态性检验和假设检验方法
Scipy库提供了多种正态性检验和假设检验方法。以下是一些常用的检验方法的列表: 正态性检验方法: Shapiro-Wilk检验:scipy.stats.shapiroAnderson-Darling检验:scipy.stats.andersonKolmogorov-Smirnov检验:scipy.st…...
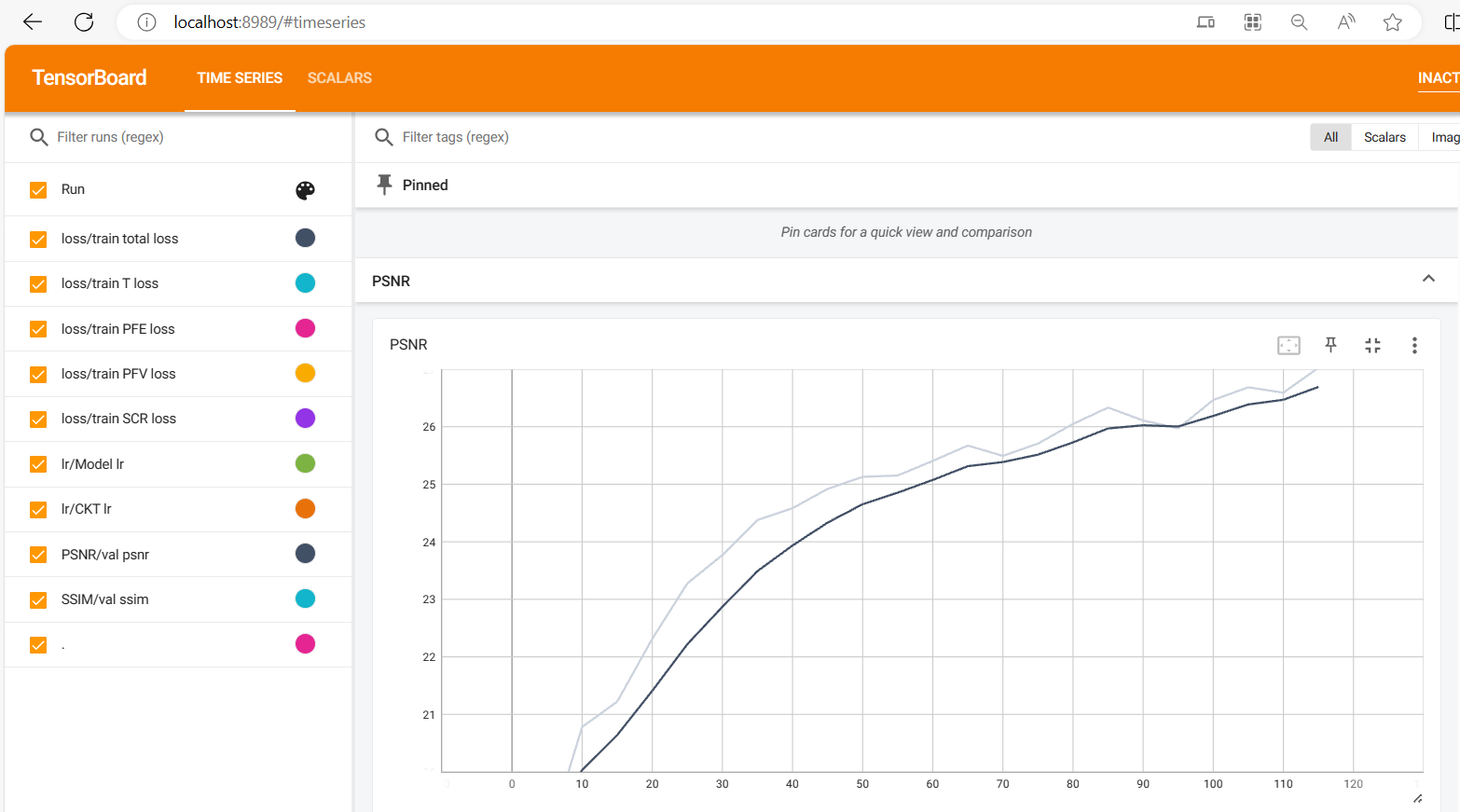
去雨去雪去雾算法之本地与服务器的TensorBoard使用教程
在进行去雨去雾去雪算法实验时,需要注意几个参数设置,num_workers只能设置为0,否则会报各种稀奇古怪的错误。 本地使用TensorBoard 此外,发现生成的文件是events.out.tfevents格式的,查询了一番得知该文件是通过Tens…...
【小沐学前端】Node.js实现基于Protobuf协议的WebSocket通信
文章目录 1、简介1.1 Node1.2 WebSocket1.3 Protobuf 2、安装2.1 Node2.2 WebSocket2.2.1 nodejs-websocket2.2.2 ws 2.3 Protobuf 3、代码测试3.1 例子1:websocket(html)3.1.1 客户端:yxy_wsclient1.html3.1.2 客户端:…...
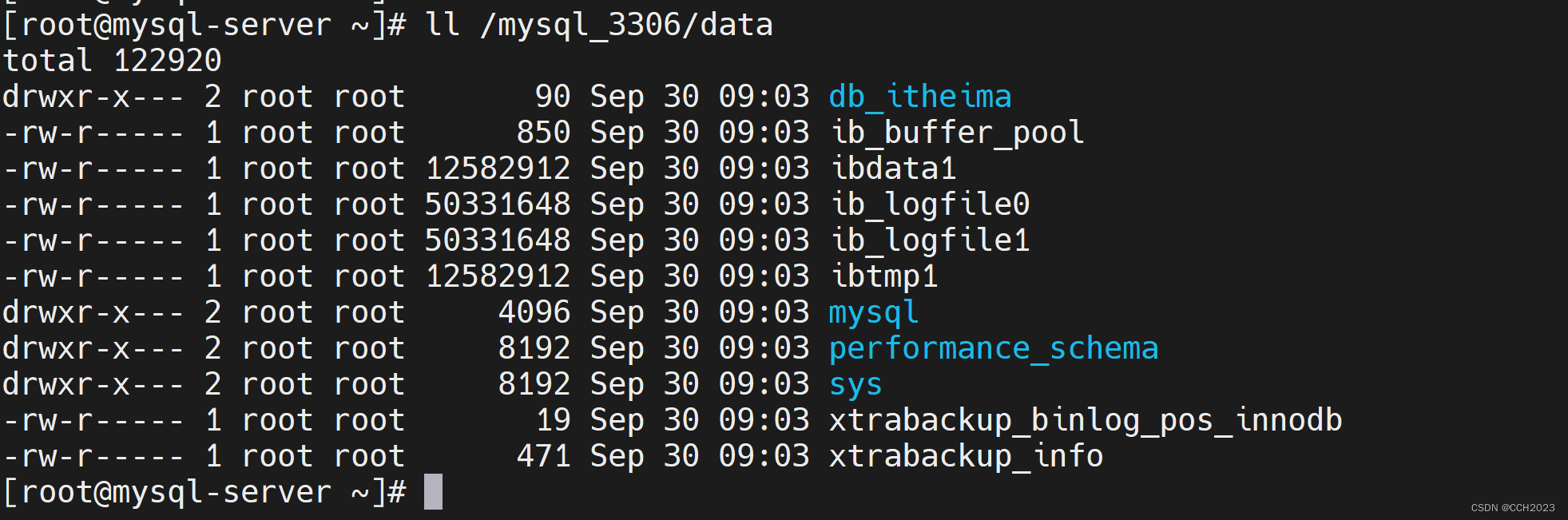
MySQL学习笔记24
MySQL的物理备份: xtrabackup备份介绍: xtrabackup优缺点: 优点: 1、备份过程快速、可靠(因为是物理备份);直接拷贝物理文件。 2、支持增量备份,更为灵活; 3、备份…...

objective-c 基础学习
目录 第一节:OC 介绍 第二节:Fundation 框架 第三节:NSLog 相对于print 的增强 第四节:NSString 第五节:oc新增数据类型 第六节: 类和对象 类的方法的声明与实现 第七节:类…...

【精彩回顾】 用sCrypt在Bitcoin上构建智能合约
2023年3月24日,sCrypt在英国Exeter大学举办了关于智能合约的大学讲学。sCrypt首席执行官刘晓晖做了题为“用sCrypt在Bitcoin上构建智能合约”的演讲,并与到场的老师、学生进行了深入交流、互动。这次课程着重讲解了 BSV 智能合约的基础概念,以…...

Kotlin 使用泛型
在 Kotlin 中,我们可以使用泛型(Generics)来编写具有通用性的代码,以增强代码的可重用性和类型安全性。通过使用泛型,我们可以在不指定具体类型的情况下编写适用于多种类型的函数和类。 以下是 Kotlin 中使用泛型的几…...
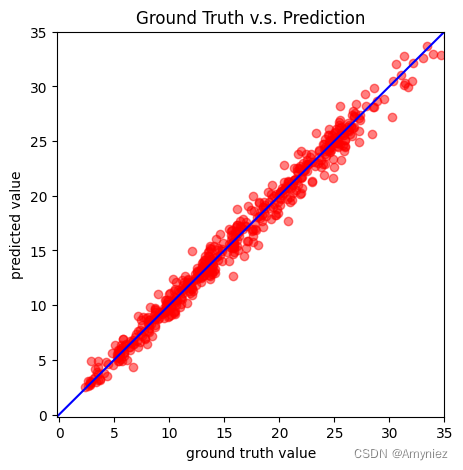
深度学习 二:COVID 19 Cases Prediction (Regression)
Deep Learning 1. 回归算法思路2. 代码2.1 基础操作2.2 定义相关函数2.3.1 定义图像绘制函数2.3.2 数据集加载及预处理2.3.3 构造数据加载器2.3.4 构建前馈神经网络(Feedforward Neural Network)模型2.3.5 神经网络的训练过程2.3.6 模型评估2.3.7 模型测…...

UG\NX二次开发 信息窗口的4种输出方式 NXOpen::ListingWindow::DeviceType
文章作者:里海 来源网站:《里海NX二次开发3000例专栏》 简介 UG\NX二次开发 信息窗口的4种输出方式 NXOpen::ListingWindow::DeviceType 信息窗口的输出类型 enum NXOpen::ListingWindow::DeviceType 枚举值描述 DeviceTypeWindow0输出将写入“信息”窗口DeviceTypeFile1输出…...

mavn打包时如何把外部依赖加进去?
一、添加依赖: <dependency><groupId>com.dm</groupId><artifactId>DmJdbcDriver</artifactId><version>18</version><scope>system</scope><systemPath>${project.basedir}/lib/DmJdbcDriver18.jar</systemP…...

爬虫代理请求转换selenium添加带有账密的socks5代理
爬虫代理请求转换selenium添加带有账密的socks5代理。 一、安装三方库 二、使用方法 1、在cmd命令行输入: 2、给selenium添加代理 最近因为工作需要,需要selenium添加带有账密的socks5代理,贴出一个可用的方法。 把带有账密的socks5代理&am…...

Redis 如何实现数据不丢失的?
Redis 实现数据不丢失的关键在于使用了多种持久化机制,以确保数据在内存和磁盘之间的持久性。以下是 Redis 实现数据不丢失的主要方法: 快照(Snapshot)持久化: Redis 使用快照持久化来定期将内存中的数据写入磁盘。快照是一个数据库状态的副本,包含了所有键和与其相关联的…...

[高等数学]同济版高等数学【第七版】上下册教材+习题全解PDF
laiyuan 「高等数学 第7版 同济大学」 https://www.aliyundrive.com/s/5fpFJb3asYk 提取码: 61ao 通过百度网盘分享的文件:同济版高数教材及… 链接:https://pan.baidu.com/s/1gyy-GMGjwguAjYijrpC8RA?pwdyhnr 提取码:yhnr 高等数学相关: The Ca…...

【面试题精讲】Java超过long类型的数据如何表示
有的时候博客内容会有变动,首发博客是最新的,其他博客地址可能会未同步,认准https://blog.zysicyj.top 首发博客地址[1] 面试题手册[2] 系列文章地址[3] 在 Java 中,如果需要表示超过 long 类型范围的数据,可以使用 BigInteger 类…...
)
Shapiro-Wilk正态性检验(Shapiro和Wilk于1965年提出)
Shapiro-Wilk正态性检验是一种用于确定数据集是否服从正态分布的统计方法。它基于Shapiro和Wilk于1965年提出的检验统计量。以下是其基本原理和用途: 基本原理: 零假设(Null Hypothesis):Shapiro-Wilk检验的零假设是数…...
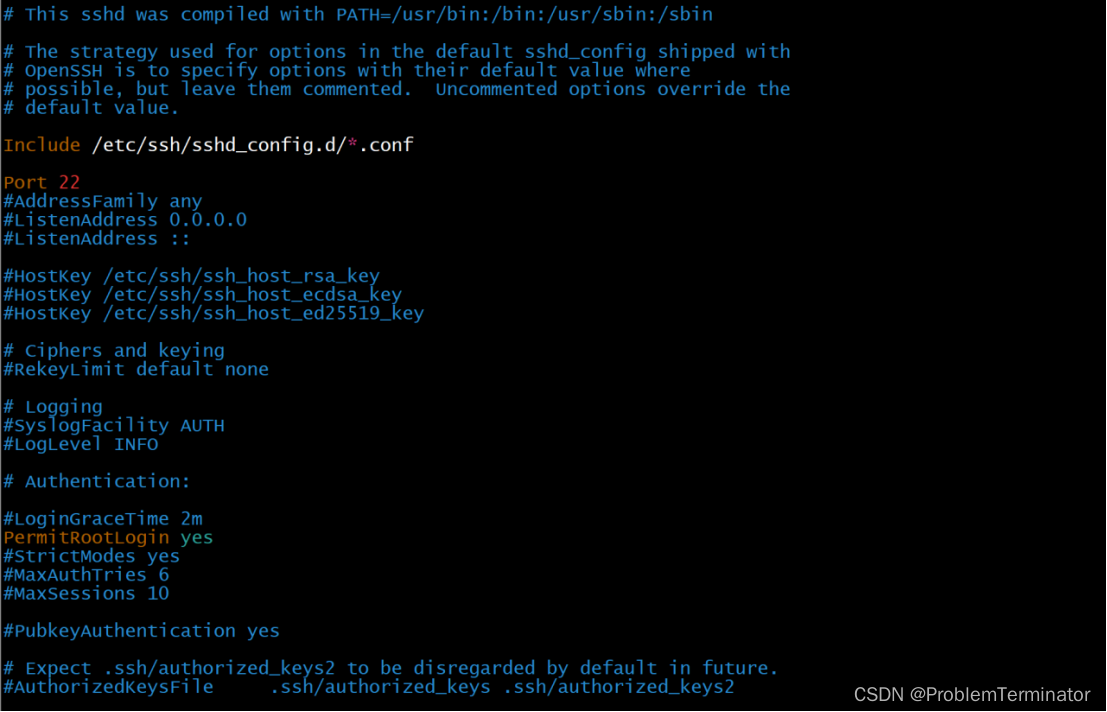
debian设置允许ssh连接
解决新debian系统安装后不能通过ssh连接的问题。 默认情况下,Debian系统不开启SSH远程登录,需要手动安装SSH软件包并设置开机启动。 > 设置允许root登录传送门:debian设置允许root登录 首先检查/etc/ssh/sshd_config文件是否存在。 注意…...

【C语言经典100例题-66】(用指针解决)输入3个数a,b,c,按大小顺序输出。
代码: #include<stdio.h> #define _CRT_SECURE_NO_WARNINGS 1//VS编译器使用scanf函数时会报错,所以添加宏定义 swap(p1, p2) int* p1, * p2; {int p;p *p1;*p1 *p2;*p2 p; } int main() {int n1, n2, n3;int* pointer1, * pointer2, * point…...

【STM32 CubeMX】移植u8g2(一次成功)
文章目录 前言一、下载u8g2源文件二、复制和更改文件2.1 复制文件2.2 修改文件u8g2_d_setup文件u8g2_d_memory 三、编写oled.c和oled.h文件3.1 CubeMX配置I2C3.2 编写文件oled.holed.c 四、测试代码main函数测试代码 总结 前言 在本文中,我们将介绍如何在STM32上成…...

华为云智能化组装式交付方案 ——金融级PaaS业务洞察及Web3实践的卓越贡献
伴随信息技术与金融业务加速的融合,企业应用服务平台(PaaS)已从幕后走向台前,成为推动行业数字化转型的关键力量。此背景下,华为云PaaS智能化组装式交付方案闪耀全场,在近日结束的华为全联接大会 2023上倍受…...
)
Halcon Image相关算子(二)
(1) dyn_threshold(OrigImage, ThresholdImage : RegionDynThresh : Offset, LightDark : ) 功能:从输入图像中选择像素满足阈值条件的那些区域。 图形输入参数:OrigImage:原始图像; 图形输入参数:ThresholdImage&a…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
