100种思维模型之诺依曼思维模型-019
生活中,难免总会遇到一些“大”、“笼统”、“难入手”的问题!
如,前几天突然接到领导安排,帮忙梳理一个材料“***景区创建5A级旅游景区提升规划”。
对于一个没有学过景区提升规划、没有做过规划的我来说,真的挺难的。但是任务接了,还是要干呀,咋办?
查资料,看类似规划包括哪些内容;请教专业人士,就具体的问题帮忙拆解;然后分项编制,最后整合定稿。
以上,这个过程就利用了“诺依曼思维模型”——一个分解解决复杂问题的思维模型。
01、何谓诺依曼思维模型
一、天才—诺依曼
诺依曼,全名约翰·冯·诺依曼(John von Neumann,1903年12月28日-1957年2月8日),美籍匈牙利数学家、计算机科学家、物理学家,是20世纪最重要的数学家之一。
他是布达佩斯大学数学博士,是现代计算机、博弈论、核武器和生化武器等领域内的科学全才之一,被后人称为“现代计算机之父”、“博弈论之父”。
他是一位天才,六岁—心算做八位数除法;八岁—掌握微积分;十岁—数月读完四十八卷的世界史……
曾有人类比在计算机领域,假如图灵发明了0到1,那么冯·诺依曼发展了从1到60,而人类计算机至今仍在冯·诺依曼体系里行走。
他提出了计算机制造的三个基本原则:1.采用二进制逻辑;2.程序存储执行;3.计算机由五个部分组成(运算器、控制器、存储器、输入设备、输出设备),如下图:

原子能委员会主席斯特劳斯曾对他做过这样的评价:他有一种使人望尘莫及的能力,最困难的问题到他手里都会被分解成一件件看起来十分简单的事情。
二、诺依曼思维
所谓诺伊曼思维,指的是将一个复杂问题拆解成一个个小细节,然后将小细节重新组合成具有某种意义指定属性的大问题。
由以上定义可知,该模型具体包括两个部分,一是把复杂大问题分解成一个个小细节;二是把一个个小细节组合成具有某种意义的大问题。
如,学生生涯做题和出题的思路,做题是将复杂问题拆分成小问题各个击破;出题是将多个小问题组合成一个大问题。
再比如,工作中,接到一个不熟悉的任务——梳理一份关于”***景区创建5A级旅游景区提升规划”的材料。
首先,按照提升规划包括的内容进行分解——政策、资源、场地和市场4个方面;其次再针对每一个继续细分,如政策包括国家层面的、区域层面的等等,如果国家层面政策多,可以继续细分,直至可以说清道明为止;最后,把分析出来的一个个小项进行整合,佐证我们想呈现出来的结果。
三、诺依曼思维模型
所谓诺依曼思维模型,就是将诺伊曼思维应用到解决问题上。
生活、工作中在遇到重要问题、重大决策时,运用诺伊曼思维进行思考,把复杂问题分解成一件件可执行的简单事情,把可执行的简单事情进行随机组合,佐证或者呈现一个新观点、新成果。
02、诺依曼思维模型生活中的运用
一、任务拆解
如,经典案例,怎么把大象放进冰箱?
第一步,打开冰箱门;第二步,把大象放进去;第三步,关上门。
再比如,小时候学骑自行车!
家长会把骑自行车这个负责问题拆解成我们能把握的小细节:
1.眼睛怎么做, 眼睛盯着前方;2.手怎么放,手把着车把;3.脚怎么做,脚用劲蹬;4.身体怎么办,身体保持平衡。
然后,我们就按照以上的小细节进行多次重复练习,慢慢地就学会了骑车。
再比如,业务部门任务拆解,目标5000万的销售额怎么拆解呢?
首先,我们来看看这个销售额怎么来的?
销售额=店员粉丝数*日转化率*客单价*300天(一年300个工作日)。
其次,我们在看看目前这家店有多少粉丝数、日转化率、客单价是多少!然后市场上找到同品类且销售额在5000左右的店铺,看对方以上三个数据情况。

绘制
由以上表格,可知我企业的客单价和日转化率已非常不错,下一步需要做的是继续维持目前的高水平,同时增加店铺粉丝数。
接下来对客单价、日转化率、店铺粉丝数继续拆解分析;
经分析,客单价高,是因为客服话术水平高,服务好;日转化率高,是因为文案写得好,图片拍得好;而粉丝数,是线上(淘宝、抖音、快手、微博、微信公号等引流)线下(上门拜访、电话回访等)引流。
所以,要实现目标5000万的任务,即从线上、线下获得7.4万新粉丝,且保持服务水平及文案、图片水平。
通过以上任务的拆解,5000万的目标就更明确了,也更容易实现了。
二、组合创新
前期,我记得我分享过这样一篇文章“十二聪明法孕育创新”——其实就是组合创新。
“加一加,减一减,扩一扩,缩一缩,变一变,改一改,联一联、学一学、代一代、搬一搬、反一反、定一定。”
其实,写文章也是一种组合创新。
我记得有一次一位记者怼美团王兴说,美团毫无创新,美团的项目来自于抄袭。王兴反驳抄袭说:那你写的文章叫创新吗?你写的每一个字都不是你创造的。
组合创新告诉我们,很多时候创新,不是绞尽脑子的去想一个新的idear,有时候把现有的一些东西做一些加加、减减、拼凑、或者将一个领域的知识运用到另一个领域等也是一种创新。
03、怎么更好的运用
一、任务“拆解”非“拆分”。
诺依曼思维模型的核心之一在于任务的拆解,把一个复杂事情拆解成一个个可执行的简单事情。
而现实运用中,我们经常会把拆解和拆分混一起,以致错误的认为任务拆解毫不作用——其实并非拆解无用,而是我们把拆分当成了拆解。
何谓拆分?拆分指的是,把一个大任务分解成几个小任务,小任务相加等于大任务。
如,一个大区的KPI是1000万销售目标,10个城市经理每人领走100万的销售任务。
何谓拆解?拆解指的是,把一个大任务还原出做成的具体小动作,小动作相乘等于大任务。
如,一个大区的KPI是1000万销售目标,实现目标1000万销售额,客单价多少,历史转化率多少,成交多少用户——继而推算出需要拜访多少客户,再拆解出可以去哪些渠道找到这些客户。
所以,要学会拆解,记住任务“拆解”非“拆分”。
二、组合目标要明确。
我发现很多优秀的人都是门儿清的人,他们知道自己需要什么,知道自己要做这件事是为了什么!
如,最近樊登老师对话直播女王薇娅,薇娅说:她会时常思考“我是谁?”,通过思考我是谁,明确自己的目标,然后对当下的行动进行决策。

再比如,最近有个朋友放弃了大公司的优越待遇,转身到了一个薪资平平的小公司,这是因为他清楚自己现阶段需要什么。
他要的是快速提升做事的能力,而这家小公司刚好具备这样的条件。
组合创新有千千万万,而我们当下能做的,我们想做的是有限的,我们要把焦点放在那些重要且主要的事情上,即专注于“影响圈”的事,并不断努力提升,扩大自己的影响圈。
04、写在最后
诺依曼模型可以应用在:学习一种新事物,解决一个复杂问题,处理一个项目,分析别人做的好的案例或文案,解读一个人做的好的地方,探究一个事物的本质,寻找策略与创意等。
任何一件复杂的事物,都是由若干微小的事物组成。任何复杂的知识,都可以通过一点一点的累积来学会。
如果遇到任何困难,请退一步,把事情拆解开来,一点一点完成。做好当下,积跬步至千里,积小流成江海。
最后,就组合创新方面,要铭记自己的目标,要专注于“影响圈”的事,并不断努力提升,扩大自己的影响圈。
相关文章:

100种思维模型之诺依曼思维模型-019
生活中,难免总会遇到一些“大”、“笼统”、“难入手”的问题! 如,前几天突然接到领导安排,帮忙梳理一个材料“***景区创建5A级旅游景区提升规划”。 对于一个没有学过景区提升规划、没有做过规划的我来说,真的挺难的…...

Python + Airtest + poco + pytest + pytest-html 实现Android App自动化测试框架
Python Airtest poco pytest pytest-html 实现Android App自动化测试框架 一、背景 为了尝试除Appium外的测试框架,本文将介绍基于网易的airtest框架为基础,配合poco及pytest实现对Android App的自动化测试。 二、框架介绍 框架集成使用airtest p…...

一篇文章让你学会spring
Spring6 1、概述 1.1、Spring是什么? Spring 是一款主流的 Java EE 轻量级开源框架 ,Spring 由“Spring 之父”Rod Johnson 提出并创立,其目的是用于简化 Java 企业级应用的开发难度和开发周期。Spring的用途不仅限于服务器端的开发。从简…...
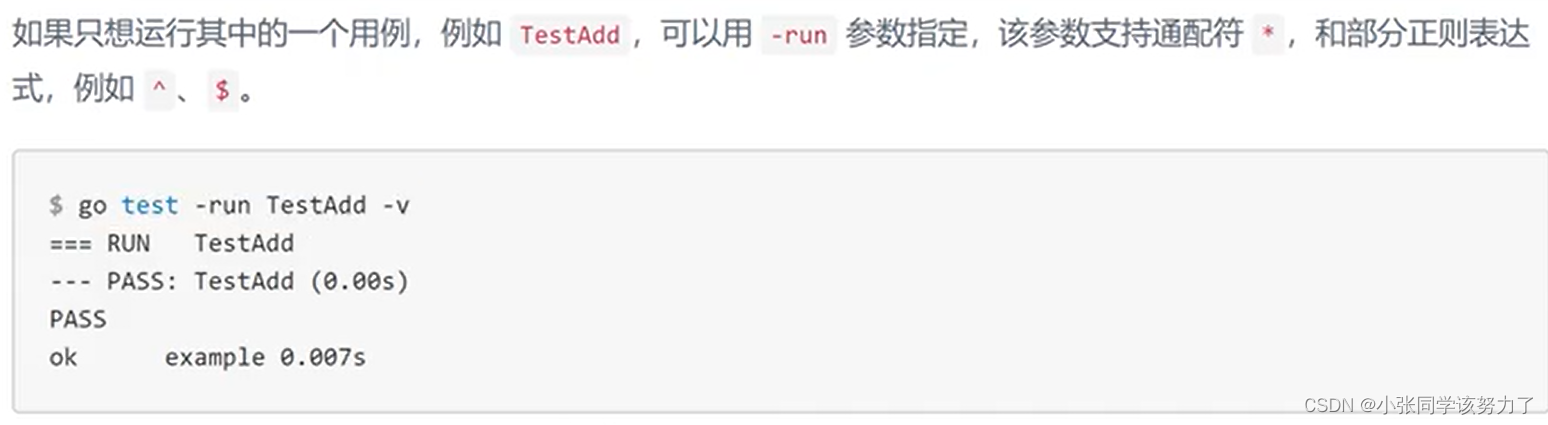
golang入门笔记——测试
测试类型: 单元测试: 规则: 1.所有测试文件以_test.go结尾 2.func Testxxx(*testing.T) 3.初始化逻辑放到TestMain中 运行: go test [flags][packages]Go语言中的测试依赖go test命令。 go test命令是一…...

【CSAPP】整数运算
文章目录无符号加法练习1练习2补码加法练习1练习2练习3练习4补码的非练习无符号乘法补码乘法练习1练习2练习3乘以常数练习1练习2除以2的幂练习1练习2关于整数运算的最后思考练习无符号加法 考虑两个非负整数x和y,满足0≤x,y<2w0 \le x, y < 2^w0≤x,y<2w&…...
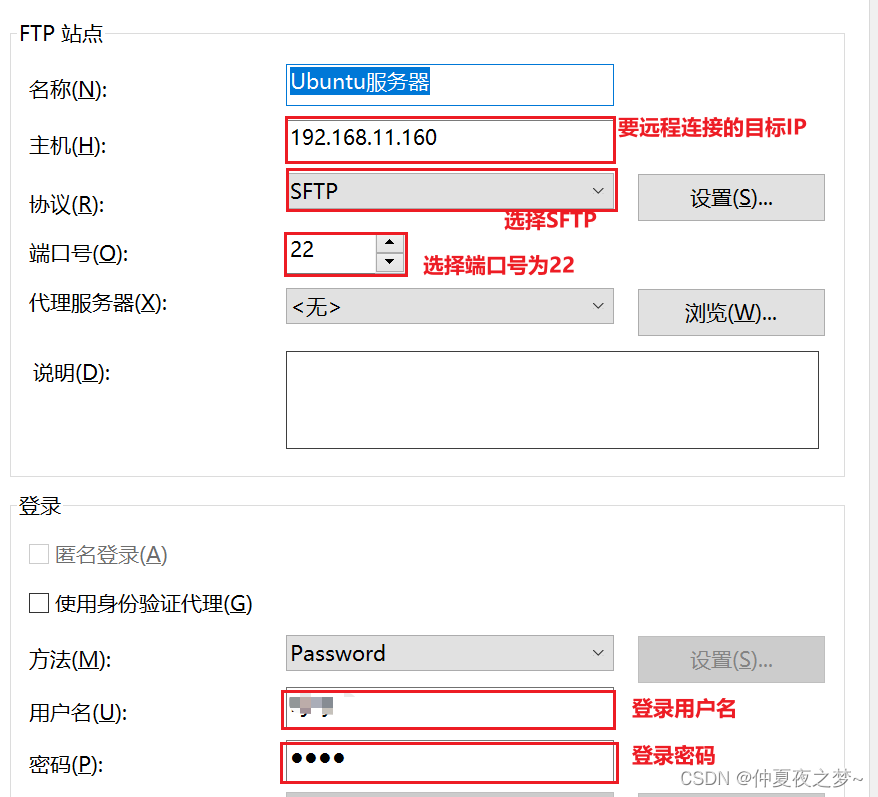
使用 xshell 远程连接(使用 xftp 远程传输)
xshell 和 xftp的使用都基于ssh协议,我们需要先在远程服务端或者虚拟机上安装ssh服务,然后才能远程连接。 目录 1、什么是ssh协议? 2、安装 openssh (1) 安装 openssh 服务器 (2) 关闭服务器防火墙(或者开放端口22)…...

一个例子搞懂子网划分及子网掩码的计算
前置知识: 1、标准ip地址分为A、B、C、D、E五类,分类标准是ip地址的前几个比特位的值。 我们知道ip地址是32位比特-4字节组成,A类地址则是由首位为0,首字节为网络地址,其余3字节为主机地址组成,A类网络地址…...
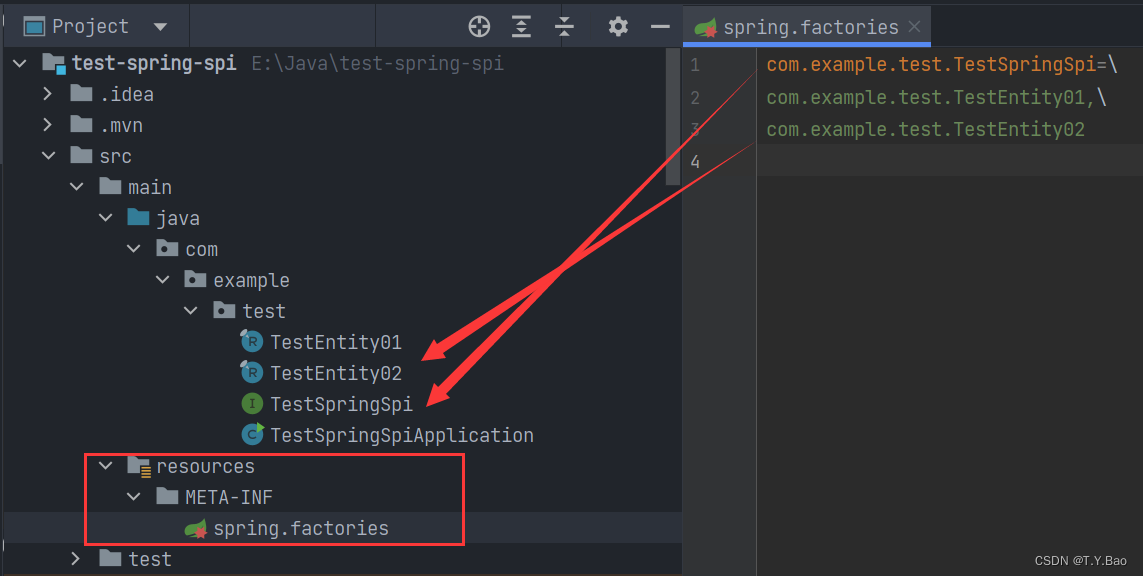
SPI机制源码:JDK Dubbo Spring
JDK 17 Dubbo 3.1.6 JDK SPI JDK SPI在sql驱动类加载、以及slf4j日志实现加载方面有具体实现。 示例 public class Test {private static final Logger logger LoggerFactory.getLogger(Test.class);public static void main(String[] args) {ServiceLoader<JdkSpiServi…...
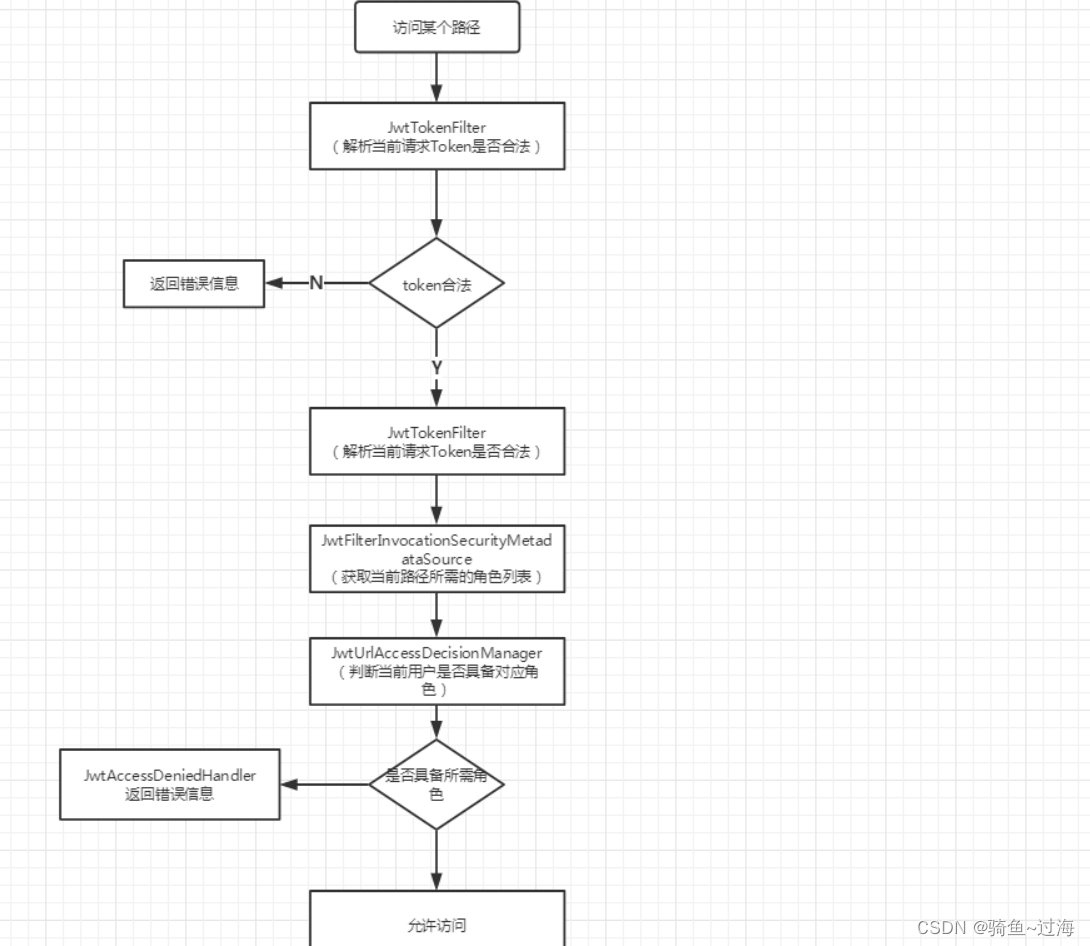
Spring Security+jwt+redis+自定义认证逻辑 权限控制
Spring Securityjwtredis自定义认证逻辑 权限控制 1.拦截访问基本思路 2.创建数据库表:角色表(应该6个表,这里只用用户表代替角色表)、权限表、路径表、角色-权限表、权限-路径表 /* SQLyog Professional v12.14 (64 bit) MySQL…...

打游戏什么蓝牙耳机好用?打游戏比较好的蓝牙耳机
游戏耳机提供身临其境的细致声音,同时也是与朋友在线聊天的绝佳通信设备,尤其对于游戏玩家来说,聆听和被聆听的最佳方式之一就是游戏耳机,那2023年到底有哪些值得购买的游戏耳机呢?现在就让我们一起来看看吧。 第一款…...
炔基点击交联试剂1704097-05-1,Alkyne-A-DSBSO crosslinker,发生相应点击反应
1、理论分析:中文名:炔基-A-DSBSO crosslinker,英文名:Alkyne-A-DSBSO crosslinkerCAS号:1704097-05-1化学式:C25H32N2O12S2分子量:616.652、产品详情:外观:白色固体&…...
)
刷题记录:牛客NC24309Overplanting (Silver)
传送门:牛客 题目描述: Farmer John has purchased a new machine that is capable of planting grass within any rectangular region of his farm that is "axially aligned" (i.e., with vertical and horizontal sides). Unfortunately, the machine malfunc…...

Spring Boot中使用Sa-Token实现轻量级登录与鉴权
1. Sa-Token 介绍 Sa-Token 是一个轻量级 Java 权限认证框架,主要解决:登录认证、权限认证、单点登录、OAuth2.0、分布式Session会话、微服务网关鉴权 等一系列权限相关问题。 功能结构图 2. 登录认证 对于一些登录之后才能访问的接口(例如&…...
《分布式技术原理与算法解析》学习笔记Day20
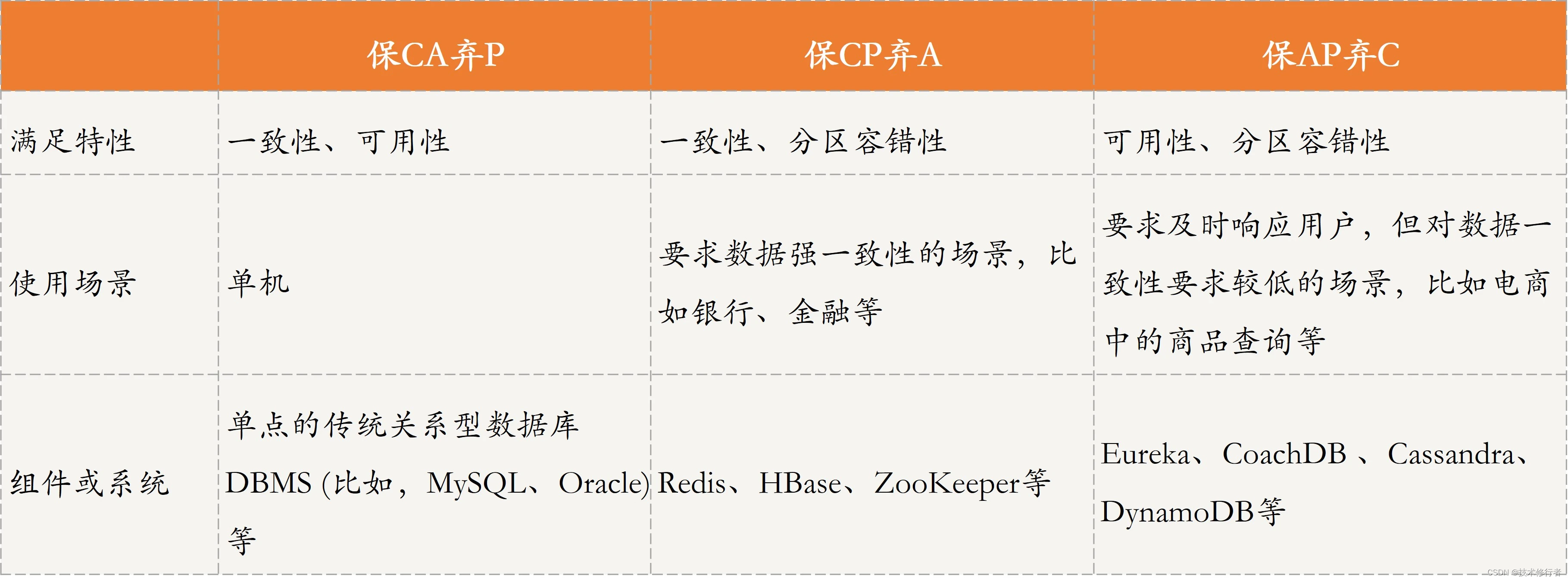
CAP理论 什么是CAP理论? CAP理论用来指导分布式系统设计,以保证系统的可用性、数据一致性等。 C,Consistency,一致性,指所有节点在同一时刻的数据是相同的,即更新操作执行结束并响应用户完成后ÿ…...

【2023-2-23】FastDeploy 安装教程
【2023-2-22】FastDeploy 安装编译教程 该测试 FastDeploy CPU版本。 1. fastDeploy库编译 1.1 官方预编译库下载 预编译库下载安装 1.2 自定义CPU版本库编译 官方编译FastDeploy教程 CMakeGUI VS 2019 IDE编译FastDeploy 本人编译教程 CMAKE_CONFIGURATION_TYPES 属性设…...

rollup.js 一个简单实用的打包工具
最近在看vue3相关的知识的时候,发现了一个新的打包工具,至少于我而言是新鲜的。它就是rollup.js。一说到JS打包、合并、压缩、模块处理等都会想到webpack,这是王者,当然入门的难度偏高。而vue3中搭配的vite运行速度确实非常快&…...
数据结构与算法之最小爬楼梯费用动态规划
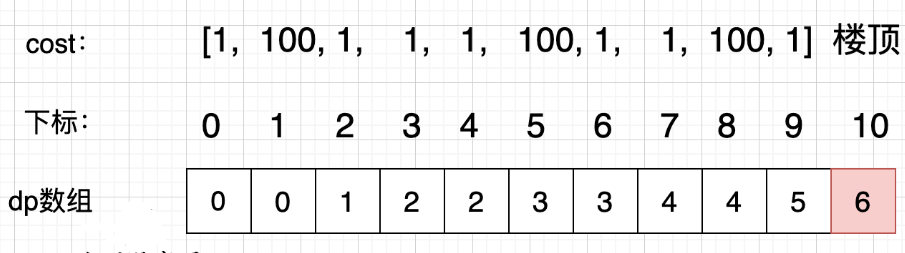
继续上一道题目,在上一道题目的基础之上,我们来解决这一道爬楼梯最小费用题。一.题目描述二.思路(动态规划五部曲)确定dp数组以及下标的含义使用动态规划,就要有一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了。dp[i]的…...

阿里云ACA认证如何获取?
获取阿里云ACA(Alibaba Cloud Certification Associate)认证,需要按照以下步骤进行操作: 注册阿里云账号。如果您还没有阿里云账号,请先注册一个账号。登录阿里云官网。登录后,进入阿里云认证中心。选择AC…...
【Python入门第十六天】Python If ... Else
Python 条件和 If 语句 Python 支持来自数学的常用逻辑条件: 等于:a b不等于:a ! b小于:a < b小于等于:a < b大于:a > b大于等于:a > b 这些条件能够以多种方式使用,…...

两数之和的解法
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。你可以按任意顺序返回答案…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...
