代码随想录 动态规划 13
300. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列
思路:由题意得知,子序列是可以删除数组中的元素的,即一段长为s的序列的最长子序列,可能与若干个元素都无关,因此 长度为s的序列的最长子序列的状态依赖于在这之前的所有长度为1,2,3,。。。s-1的状态。转移方程,由于要求的是最长严格递增子序列,那么不难想到,如果当前的元素比遍历到的元素的元素大,那么就可以将其放到该元素的后面,形成一个严格递增子序列。既然如此,dp数组的定义就定义为,dp[i] 为 以 nums[i]结尾的最长子序列,转移方程为 if nums[i] > nums[j], dp[i] = max(dp[i], dp[j] + 1),初始化为1. 使用result来记录dp数组中的最大值。
class Solution:def lengthOfLIS(self, nums: List[int]) -> int:dp = [1 for _ in range(len(nums))]result = 1for i in range(1, len(dp)):for j in range(i):if nums[i] > nums[j]:dp[i] = max(dp[i], dp[j] + 1)result = max(dp[i], result)return result674. 最长连续递增序列
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
思路:与上一题类似,dp[i]的定义为 以nums[i]为结尾的连续递增子序列长度,转移方程为,当nums[i] > nums[i-1], dp[i] = dp[j] + 1, 以result记录dp数组最大值
class Solution:def findLengthOfLCIS(self, nums: List[int]) -> int:dp = [1 for _ in range(len(nums))]result = 1for i in range(1, len(dp)):if nums[i] > nums[i-1]:dp[i] = dp[i-1] + 1result = max(dp[i], result)return result
718. 最长重复子数组
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
思路:设置dp[i][j] 为 nums1 前i -1个元素 和 nums2 前 j -1个元素 的公共最长重复子数组,那么转移方程为 if nums1[i-1] == nums2[j-1] , dp[i][j] = dp[i-1][j-1], 由于dp数组的设置,遍历时由1开始,len(nums1)+1 结束 (左闭右开)
二维dp
class Solution:def findLength(self, nums1: List[int], nums2: List[int]) -> int:dp = [[0] * (len(nums2) + 1) for _ in range(len(nums1) + 1)]result = 0for i in range(1, len(nums1) + 1):for j in range(1, len(nums2) + 1):if nums1[i-1] == nums2[j-1]:dp[i][j] = dp[i-1][j-1] + 1result = max(result, dp[i][j])return result一维dp
class Solution:def findLength(self, nums1: List[int], nums2: List[int]) -> int:dp = [0] * (len(nums2) + 1)result = 0# 遍历数组 nums1for i in range(1, len(nums1) + 1):# 倒序遍历数组 nums2for j in range(len(nums2), 0, -1):if nums1[i-1] == nums2[j-1]:dp[j] = dp[j-1] + 1result = max(dp[j], result)else:dp[j] = 0return result相关文章:

代码随想录 动态规划 13
300. 最长递增子序列 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子…...
lv6 嵌入式开发-Flappy bird项目
目录 1 项目功能总结 2 知识储备: 3 项目框图 4 Ncurses库介绍 做Flappy bird项目有什么用? 1. 复习、巩固c语言知识 2. 培养做项目的逻辑思维能力 3. 具备开发简单小游戏的能力 学会了Flappy bird项目,贪吃蛇和推房子两款小游戏也可…...

【Java】方法重写
概述 子类中出现了和父类一模一样的方法 当子类需要父类的功能,而功能主体中,子类有自己独特的内容,就可以通过重写父类中的方法,这样即延续了父类的功能,又定义了自己的特有内容 Override 是一个注解,可以…...

艺术表现形式
abstract expressionism 抽象表现主义 20世纪中期的一种艺术运动,包括多种风格和技巧,特别强调艺术家通过非传统和通常非具象的手段表达态度和情感的自由。 抽象表现主义用有力的笔触和滴落的颜料来表达情感和自发性。 简单地结合“abstract expression…...

PHP 反序列化漏洞:手写序列化文本
文章目录 参考环境序列化文本Scalar Type整数浮点数布尔值字符串 Compound Type数组数据结构序列化文本 对象数据结构序列化文本 Special TypeNULL数据结构序列化文本 手写序列化文本过程中的注意事项个数描述须于现实相符序列化文本前缀的大小写变化符号公共属性 参考 项目描…...
react.js在visual code 下的hello World
想学习reacr.js ,就开始做一个hello world。 我的环境是visual code ,所以我找这个环境下的例子。参照: https://code.visualstudio.com/docs/nodejs/reactjs-tutorial 要学习react.js ,还得先安装node.js,我在visual …...
CocosCreator3.8研究笔记(二十四)CocosCreator 动画系统-动画编辑器实操-关键帧实现动态水印动画效果
上一篇,我们介绍了动画编辑器相关功能面板说明,感兴趣的朋友可以前往阅读: CocosCreator3.8研究笔记(二十三)CocosCreator 动画系统-动画编辑器相关功能面板说明。 熟悉了动画编辑器的基础操作,那么再使用动…...

第1篇 目标检测概述 —(3)YOLO系列算法
前言:Hello大家好,我是小哥谈。YOLO(You Only Look Once)系列算法是一种目标检测算法,主要用于实时物体检测。相较于传统的目标检测算法,YOLO具有更快的检测速度和更高的准确率。YOLO系列算法的核心思想是将…...

SpringBoot整合数据库连接
JDBC 1、SQL准备 DROP TABLE IF EXISTS t_book;CREATE TABLE t_book (book_id int(11) NOT NULL,book_name varchar(255) DEFAULT NULL,price int(11) DEFAULT NULL,stock int(11) DEFAULT NULL ) ENGINEInnoDB DEFAULT CHARSETutf8mb4;/*Data for the table t_book */insert…...

uni-app:canvas-绘制图形4(获取画布宽高,根据画布宽高进行图形绘制)
效果 代码 var width ; var height ; const query uni.createSelectorQuery(); //获取宽度 query.select(#firstCanvas).fields({ size: true }, (res) > { width res.width; height res.height; }).exec(); console.log(宽度width); console.log(高…...

EM@坐标@函数@图象的对称和翻折变换
文章目录 abstract翻折变换关于坐标轴翻折 f ( − x ) , f ( x ) f(-x),f(x) f(−x),f(x) − f ( x ) , f ( x ) -f(x),f(x) −f(x),f(x) 偶函数奇函数小结 其他翻折变换关于 y x y\pm x yx对称的直角坐标 关于 x u 对称 关于xu对称 关于xu对称的函数关于 y v yv yv对称的两…...

Python之json模块
JSON (JavaScript Object Notation),由 RFC 7159 (它取代了 RFC 4627) 和 ECMA-404 指定,是一个受 JavaScript 的对象字面值句法启发的轻量级数据交换格式。JSON独立于编程语言的文本格式来存储和表示数据,现在大部分的数据传输基本使用的都是…...
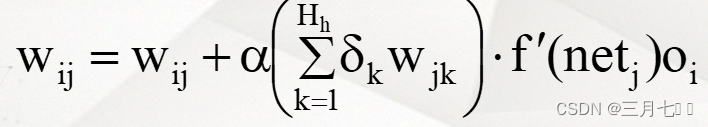
机器学习---BP算法
1. 多级网络 层号确定层的高低:层号较小者,层次较低,层号较大者,层次较高。 输入层:被记作第0层。该层负责接收来自网络外部的信息。 第j层:第j-1层的直接后继层(j>0)ÿ…...

继苹果、联发科后,传高通下一代5G芯片将由台积电以3纳米代工
台积电3纳米又有重量级客户加入。市场传出,继苹果、联发科之后,手机芯片大厂高通下一代5G旗舰芯片也将交由台积电以3纳米生产,最快将于10月下旬发表,成为台积电3纳米第三家客户。 针对相关传闻,至昨日(25日…...
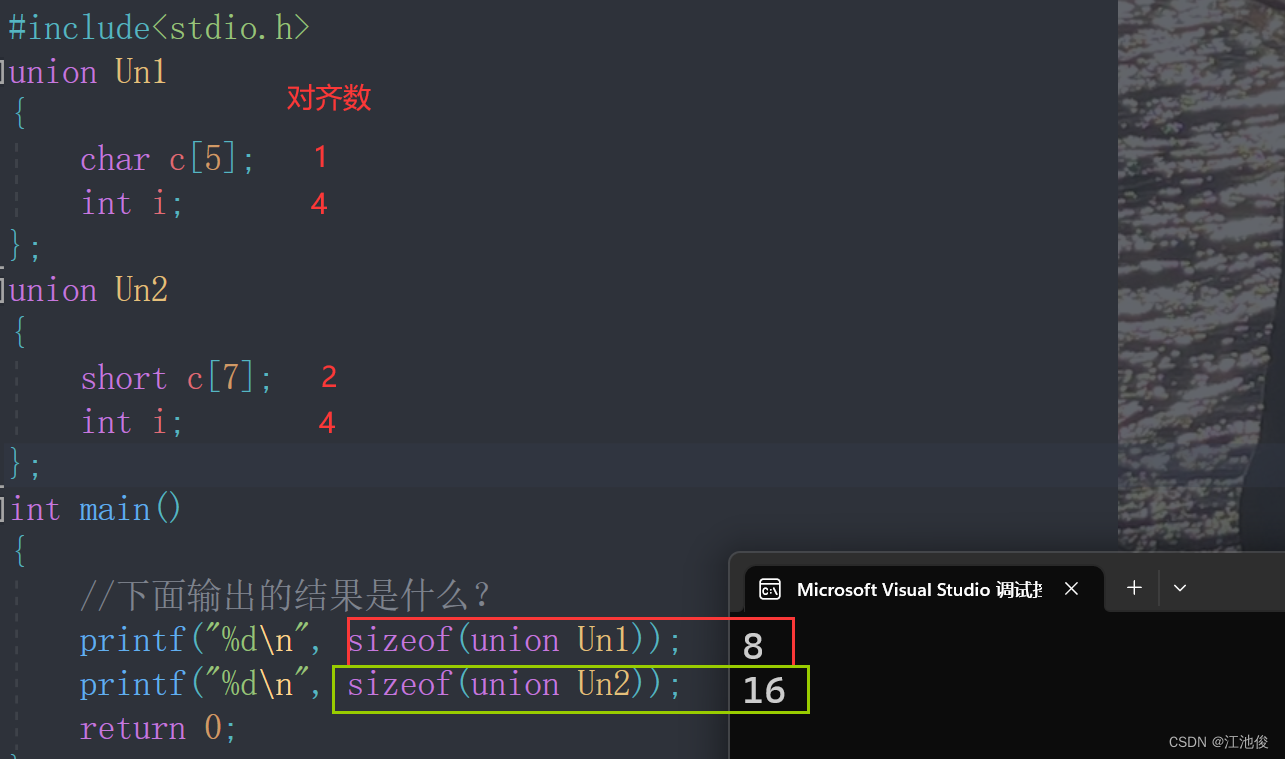
【自定义类型】--- 位段、枚举、联合
💓博客主页:江池俊的博客⏩收录专栏:C语言进阶之路👉专栏推荐:✅C语言初阶之路 ✅数据结构探索💻代码仓库:江池俊的代码仓库🎉欢迎大家点赞👍评论📝收藏⭐ 文…...
区块链(9):java区块链项目的Web服务实现之实现web服务
1 引入pom依赖 <dependency><groupId>org.eclipse.jetty</groupId><artifactId>jetty-server</artifactId><version>9.4.8.v20171121</version></dependency><dependency><groupId>org.eclipse.jetty</groupId…...

【CV】各种库安装报错及解决办法
目录 1.Error:Cannot unpack file… 1.Error:Cannot unpack file… 使用命令pip install -i https://pypi.tuna.tsinghua.edu.cn/simple --trusted-host pypi.tuna.tsinghua.edu.cn 包名安装 参考:解决Python使用pip安装库文件出现“Error&a…...
【算法系列篇】哈希表
文章目录 前言1. 两数之和1.1 题目要求1.2 做题思路1.3 Java代码实现 2. 判断是否为字符重排2.1 题目要求2.2 做题思路2.3 Java代码实现 3. 存在重复元素3.1 题目要求3.2 做题思路3.3 Java代码实现 4. 存在重复元素II4.2 题目要求4.2 做题思路4.3 Java代码实现 5. 字母异位词分…...
计算机视觉——飞桨深度学习实战-起始篇
后面我会直接跳到实战项目,将计算机视觉的主要任务和目标都实现一遍,但是需要大家下去自己多理解和学习一下。例如,什么是深度学习,什么是计算机视觉,什么是自然语言处理,计算机视觉的主要任务有哪些&#…...

vscode中运行脚手架项目报表
必选在cmd页面里面安装脚手架离谱啊,不然无法执行npm命令啊 vscode运行vue项目_小何不秃头06的博客-CSDN博客 finereport激活成功 - 帆软 (fanruan.com)...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
