EM@坐标@函数@图象的对称和翻折变换
文章目录
abstract
- 坐标@函数@图象的对称和翻折变换
翻折变换
关于坐标轴翻折
- 此处我们通过研究图象上的点来间接图象变换,设图象的方程为 y = f ( x ) y=f(x) y=f(x), f ( x ) f(x) f(x)的定义域为 D f D_f Df
f ( − x ) , f ( x ) f(-x),f(x) f(−x),f(x)
- 函数 f ( − x ) f(-x) f(−x)可以看作是函数 u = − x u=-x u=−x和 y = f ( u ) y=f(u) y=f(u)复合而成的函数
- x ∈ D u = R x\in{D_u}=\mathbb{R} x∈Du=R
- 设函数 f ( x ) f(x) f(x)的定义域为 D f {D_f} Df,对于 g ( x ) = f ( − x ) g(x)=f(-x) g(x)=f(−x), − x ∈ D f -x\in{D_f} −x∈Df,即 x ∈ − D f x\in{-D_f} x∈−Df或作 D g = − D f D_g=-D_f Dg=−Df(表示 f , g f,g f,g的定义域关于原点对称)
- 若 a ∈ D f a\in{D_f} a∈Df,在 x = a x=a x=a处,可以取函数 f ( x ) f(x) f(x)上的点 A ( a , f ( a ) ) A(a,f(a)) A(a,f(a));
- − a ∈ D g -a\in{D_g} −a∈Dg, g ( x ) g(x) g(x)上一定存在点 B ( − a , f ( a ) ) B(-a,f(a)) B(−a,f(a));
- 显然 A , B A,B A,B关于 y y y轴对称,对定义域内所有 x x x对应的点 ( x , f ( x ) ) (x,f(x)) (x,f(x))和 ( x , f ( − x ) ) (x,f(-x)) (x,f(−x))关于y轴对称
- 从而 f ( x ) , g ( x ) f(x),g(x) f(x),g(x)关于 y y y轴对称,即 f ( x ) , f ( − x ) f(x),f(-x) f(x),f(−x)关于 y y y轴对称
- 例如:
- f ( x ) = sin ( x ) f(x)=\sin(x) f(x)=sin(x),则 f ( − x ) = sin ( − x ) = − sin x f(-x)=\sin(-x)=-\sin{x} f(−x)=sin(−x)=−sinx和 f ( x ) = sin ( x ) f(x)=\sin(x) f(x)=sin(x)关于 y y y轴对称
- 对于 f ( x ) = cos x f(x)=\cos{x} f(x)=cosx, f ( − x ) = cos ( − x ) f(-x)=\cos{(-x)} f(−x)=cos(−x)= cos x \cos{x} cosx, f ( − x ) , f ( x ) f(-x),f(x) f(−x),f(x)关于 y y y轴对称,即函数 cos x \cos{x} cosx自身关于 y y y轴对称
− f ( x ) , f ( x ) -f(x),f(x) −f(x),f(x)
- 和上面的分析类似,取点分析:若函数 f ( x ) f(x) f(x),上存在 A ( a , f ( a ) ) A(a,f(a)) A(a,f(a)),则函数 − f ( x ) -f(x) −f(x)上一定相应地存在 B ( a , − f ( a ) ) B(a,-f(a)) B(a,−f(a))
- 显然两点关于 x x x轴对称,而 x x x是定义域内的任意点,故而 − f ( x ) -f(x) −f(x)和 f ( x ) f(x) f(x)关于 x x x轴对称
偶函数@奇函数
- 偶函数:若函数 f ( x ) f(x) f(x)的定义域关于原点对称且满足 f ( − x ) = f ( x ) f(-x)=f(x) f(−x)=f(x),则函数 f ( x ) f(x) f(x)是偶函数,显然 f ( x ) f(x) f(x)关于 y y y轴对称
- 若 f ( − x ) = f ( x ) f(-x)=f(x) f(−x)=f(x),那么 f ( − x ) , f ( x ) f(-x),f(x) f(−x),f(x)关于 y y y轴对称就变成了 f ( x ) , f ( x ) f(x),f(x) f(x),f(x)关于 y y y轴对称( f ( x ) f(x) f(x)和 f ( − x ) f(-x) f(−x)重合),即 f ( x ) f(x) f(x)关于 y y y轴对称
- 奇函数:若函数 f ( x ) f(x) f(x)的定义域关于原点对称且满足 f ( − x ) = − f ( x ) f(-x)=-f(x) f(−x)=−f(x),则函数 f ( x ) f(x) f(x)是奇函数,显然 f ( x ) f(x) f(x)关于坐标原点对称
- 可以 f ( x ) f(x) f(x)关于原点对称的图形理解为两部分: f ( x ) f(x) f(x)关于 y y y轴对称的图形和 f ( x ) f(x) f(x)关于 x x x轴对称的图形如果重合,那么 f ( x ) f(x) f(x)就是关于原点对称的奇函数
小结
- The graph of f ( − x ) f(−x) f(−x) is the mirror image of the graph of f ( x ) f(x) f(x) with respect to the vertical axis.
- The graph of − f ( x ) −f(x) −f(x) is the mirror image of the graph of f ( x ) f(x) f(x) with respect to the horizontal axis.
- A function is called even if f ( − x ) = f ( x ) f(−x)=f(x) f(−x)=f(x) for all x x x (For example, cos ( x ) \cos(x) cos(x)).
- A function is called odd if f ( − x ) = − f ( x ) f(−x)=−f(x) f(−x)=−f(x) for all x x x (For example, sin ( x ) \sin(x) sin(x)).
其他翻折变换
关于 y = ± x y=\pm x y=±x对称的直角坐标
- A ( x , y ) A(x,y) A(x,y)关于 y = x y=x y=x的对称点坐标 B ( y , x ) B(y,x) B(y,x)
- A ( x , y ) A(x,y) A(x,y)关于 y − x y-x y−x的对称点坐标 B ( − y , − x ) B(-y,-x) B(−y,−x)
关于 x = u 对称 关于x=u对称 关于x=u对称的函数
-
若 f ( x ) f(x) f(x)关于 x = u x=u x=u对称:
- f ( x ) f(x) f(x)的定义域关于 x = u x=u x=u对称
-
若 x 1 , x 2 x_1,x_2 x1,x2关于 u u u对称,则 x 1 + x 2 = 2 u x_1+x_2=2u x1+x2=2u,反之亦然
- 设 A ( a , f ( a ) ) A(a,f(a)) A(a,f(a))是 f ( x ) f(x) f(x)上的点,则 A A A关于对称轴 x = u x=u x=u的对称点 B ( 2 u − a , f ( a ) ) B(2u-a,f(a)) B(2u−a,f(a))也必然在 f ( x ) f(x) f(x)上
- 从而 f ( 2 u − a ) f(2u-a) f(2u−a)= f ( a ) f(a) f(a)
- 由于 a a a是定义域内的任意点,所以 f ( 2 u − x ) = f ( x ) f(2u-x)=f(x) f(2u−x)=f(x)
- 即,满足:
- 定义域关于 x = u x=u x=u对称
- f ( 2 u − x ) f(2u-x) f(2u−x)= f ( x ) f(x) f(x)
- 的函数是关于 x = u x=u x=u对称的函数
-
例如 y ( x ) = ( x − 1 ) 2 y(x)=(x-1)^2 y(x)=(x−1)2; y ( 2 − x ) = ( ( 2 − x ) − 1 ) 2 = ( 1 − x ) 2 = ( x − 1 ) 2 y(2-x)=((2-x)-1)^2=(1-x)^2=(x-1)^2 y(2−x)=((2−x)−1)2=(1−x)2=(x−1)2,即 y ( x ) = y ( 2 − x ) y(x)=y(2-x) y(x)=y(2−x),对称轴为 u = 1 2 ⋅ 2 = 1 u=\frac{1}{2}\cdot2=1 u=21⋅2=1
- 特别的,偶函数关于 x = 0 x=0 x=0对称, f ( x ) = f ( − x ) f(x)=f(-x) f(x)=f(−x),对称轴 x = u = 0 x=u=0 x=u=0,因为 x + ( − x ) = 2 u = 0 ; u = 0 x+(-x)=2u=0;u=0 x+(−x)=2u=0;u=0
关于 y = v y=v y=v对称的两个函数
- 若 f 1 ( x ) , f 2 ( x ) f_1(x),f_2(x) f1(x),f2(x)在定义域内满足 f 1 ( x ) + f 2 ( x ) = 2 v f_1(x)+f_2(x)=2v f1(x)+f2(x)=2v,则 f 1 ( x ) , f 2 ( x ) f_1(x),f_2(x) f1(x),f2(x)关于 y = v y=v y=v对称
相关文章:

EM@坐标@函数@图象的对称和翻折变换
文章目录 abstract翻折变换关于坐标轴翻折 f ( − x ) , f ( x ) f(-x),f(x) f(−x),f(x) − f ( x ) , f ( x ) -f(x),f(x) −f(x),f(x) 偶函数奇函数小结 其他翻折变换关于 y x y\pm x yx对称的直角坐标 关于 x u 对称 关于xu对称 关于xu对称的函数关于 y v yv yv对称的两…...

Python之json模块
JSON (JavaScript Object Notation),由 RFC 7159 (它取代了 RFC 4627) 和 ECMA-404 指定,是一个受 JavaScript 的对象字面值句法启发的轻量级数据交换格式。JSON独立于编程语言的文本格式来存储和表示数据,现在大部分的数据传输基本使用的都是…...
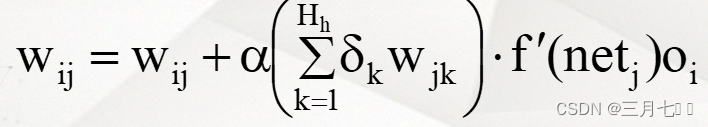
机器学习---BP算法
1. 多级网络 层号确定层的高低:层号较小者,层次较低,层号较大者,层次较高。 输入层:被记作第0层。该层负责接收来自网络外部的信息。 第j层:第j-1层的直接后继层(j>0)ÿ…...

继苹果、联发科后,传高通下一代5G芯片将由台积电以3纳米代工
台积电3纳米又有重量级客户加入。市场传出,继苹果、联发科之后,手机芯片大厂高通下一代5G旗舰芯片也将交由台积电以3纳米生产,最快将于10月下旬发表,成为台积电3纳米第三家客户。 针对相关传闻,至昨日(25日…...
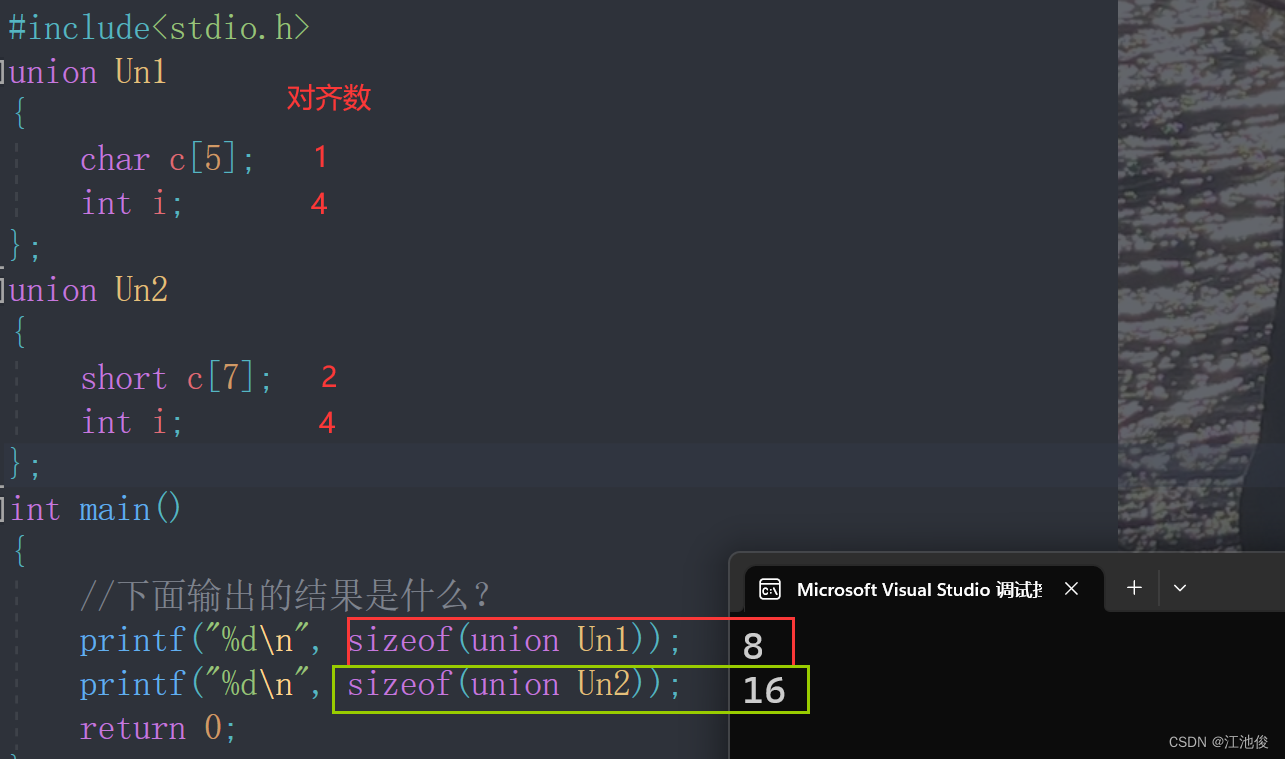
【自定义类型】--- 位段、枚举、联合
💓博客主页:江池俊的博客⏩收录专栏:C语言进阶之路👉专栏推荐:✅C语言初阶之路 ✅数据结构探索💻代码仓库:江池俊的代码仓库🎉欢迎大家点赞👍评论📝收藏⭐ 文…...
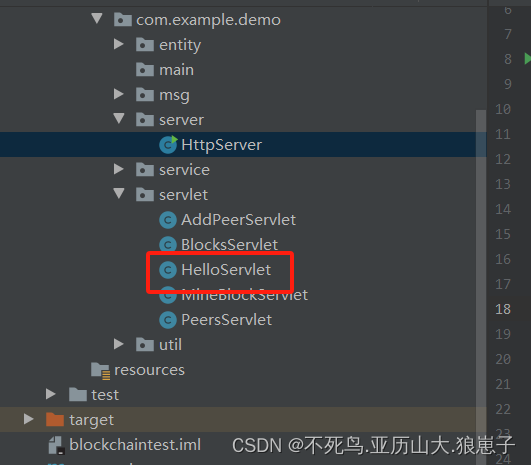
区块链(9):java区块链项目的Web服务实现之实现web服务
1 引入pom依赖 <dependency><groupId>org.eclipse.jetty</groupId><artifactId>jetty-server</artifactId><version>9.4.8.v20171121</version></dependency><dependency><groupId>org.eclipse.jetty</groupId…...

【CV】各种库安装报错及解决办法
目录 1.Error:Cannot unpack file… 1.Error:Cannot unpack file… 使用命令pip install -i https://pypi.tuna.tsinghua.edu.cn/simple --trusted-host pypi.tuna.tsinghua.edu.cn 包名安装 参考:解决Python使用pip安装库文件出现“Error&a…...
【算法系列篇】哈希表
文章目录 前言1. 两数之和1.1 题目要求1.2 做题思路1.3 Java代码实现 2. 判断是否为字符重排2.1 题目要求2.2 做题思路2.3 Java代码实现 3. 存在重复元素3.1 题目要求3.2 做题思路3.3 Java代码实现 4. 存在重复元素II4.2 题目要求4.2 做题思路4.3 Java代码实现 5. 字母异位词分…...
计算机视觉——飞桨深度学习实战-起始篇
后面我会直接跳到实战项目,将计算机视觉的主要任务和目标都实现一遍,但是需要大家下去自己多理解和学习一下。例如,什么是深度学习,什么是计算机视觉,什么是自然语言处理,计算机视觉的主要任务有哪些&#…...

vscode中运行脚手架项目报表
必选在cmd页面里面安装脚手架离谱啊,不然无法执行npm命令啊 vscode运行vue项目_小何不秃头06的博客-CSDN博客 finereport激活成功 - 帆软 (fanruan.com)...

中睿天下荣获2023全国智能驾驶测试赛车联网安全比赛第一名
9月24日,由工业和信息化部、公安部、交通运输部、中国科学技术协会、北京市人民政府共同主办的2023世界智能网联汽车大会展览会在北京闭幕。同期举行的全国智能驾驶测试赛(京津冀赛区)宣布比赛结果,中睿天下凭借过硬的产品实力&am…...
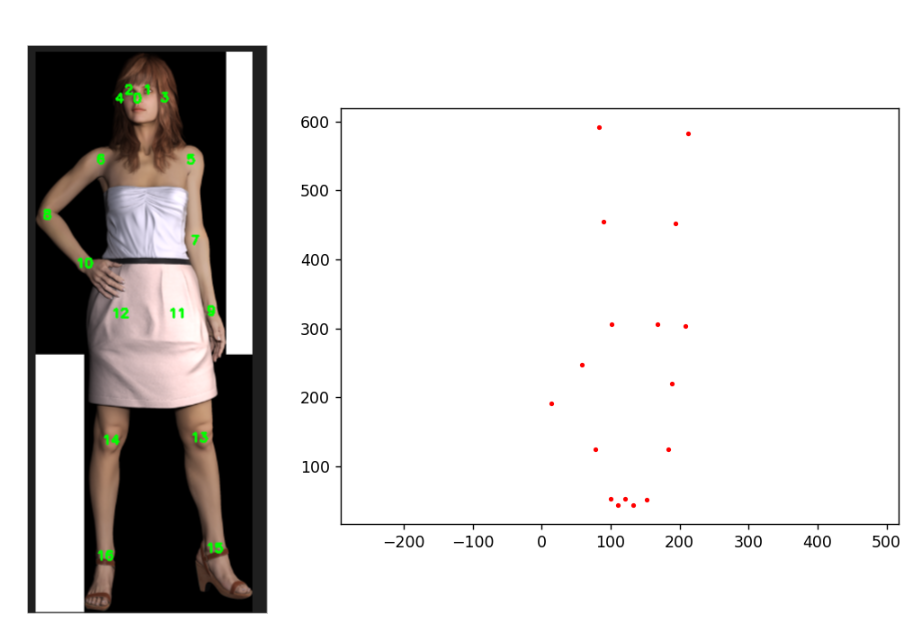
opencv图像数组坐标系
在OpenCV的Python接口(cv2)中,加载的图像数组遵循以下坐标系和方向约定: 1. **坐标系:** OpenCV的坐标系遵循数学中的坐标系,原点(0, 0)位于图像的左上角。横轴(X轴&…...
zookeeper mac安装
目录 1.下载zookeeper安装包 2.解压安装包 3.修改配置文件 4.启动服务端 5.启动客户端 这边工作中用到了zookeeper组件,但自己独立安装弄的不太多,这边本机mac装一个做测试使用 以下是安装记录,可以作为参考 从以下链接zookeeper版本列…...

js生成随机16进制数
在JavaScript中,可以使用以下的代码来生成一个100位的随机十六进制数: function generateRandomHex(length) {var result ;var characters 0123456789abcdef;for (var i 0; i < length; i) {result characters.charAt(Math.floor(Math.random() …...
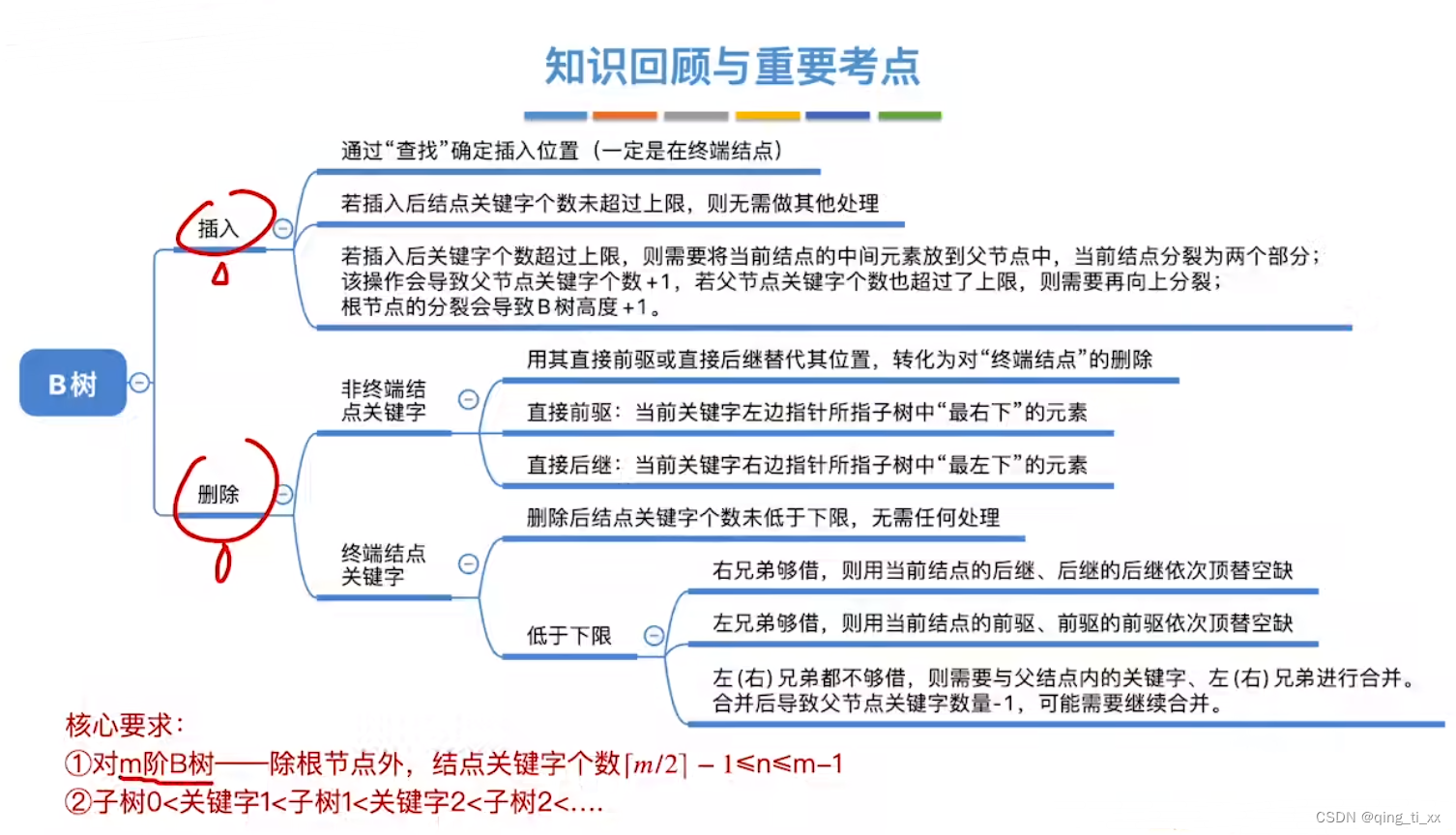
第七章 查找 八、B树
目录 一、定义 二、B树的核心特性 1、B树各个结点的子树数和关键字数 2、子树高度 3、关键字的值 4、B树高度 三、B树的插入 四、B树的删除 一、定义 B树,又称多路平衡查找树,B树中所有结点的孩子个数的最大值称为B树的阶,通常用m表示…...

Vue以及整合ElementUI
初始化vue项目 #vue 脚手架使用 webpack 模板初始化一个 appname 项目 vue init webpack appname启动 vue 项目 #项目的 package.json 中有 scripts,代表我们能运行的命令 npm start npm run dev #启动项目 npm run build:将项目打包项目结构 运行流程…...
免费、丰富、便捷的资源论坛——Yiove论坛,包括但不限于阿里云盘、夸克云盘、迅雷云盘等等
引言 目前资源的数量达到了60000,六万多的资源意味着在这里几乎可以找到任何你想要的资源。 当然,资源并不是论坛的全部,其中还包括了技术交流、福利分享、最新资讯等等。 传送门:YiOVE论坛 - 一个有资源有交流,有一…...

1.3 互联网的组成
思维导图: 前言: 我的笔记: #### 一、总览 - **互联网的结构**: - 具有全球覆盖和复杂的拓扑结构。 - 即便结构复杂,还是可以从工作方式上简化为两大部分:边缘部分和核心部分。 #### 二、边缘部分 -…...
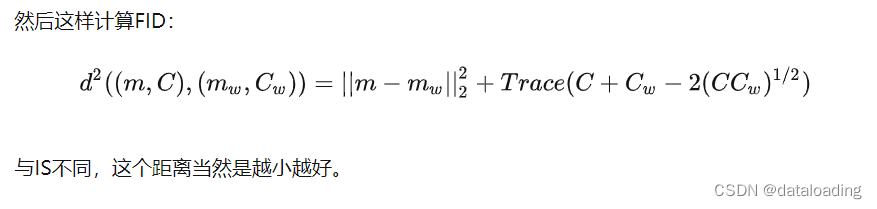
【机器学习】熵和概率分布,图像生成中的量化评估IS与FID
详解机器学习中的熵、条件熵、相对熵、交叉熵 图像生成中常用的量化评估指标通常有Inception Score (IS)和Frchet Inception Distance (FID) Inception Score (IS) 与 Frchet Inception Distance (FID) GAN的量化评估方法——IS和FID,及其pytorch代码...
Vue3.0跨端Web SDK访问微信小程序云储存,文件上传路径不存在/文件受损无法显示问题(已解决)
整理需求: 需要vue3.0作为pc端的后台管理来连接微信小程序客户端需要Web SDK的引入,实现vue3.0接入云开发环境需要以云环境作为线上服务器,将vue3.0上传的本地文件通过云环境进入云储存,并将文件在云端生成云端快捷访问路径及htt…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...
