【算法与数据结构(C语言)】栈和队列
文章目录
目录
前言
一、栈
1.栈的概念及结构
2.栈的实现
入栈
出栈
获取栈顶元素
获取栈中有效元素个数
检测栈是否为空,如果为空返回非零结果,如果不为空返回0
销毁栈
二、队列
1.队列的概念及结构
2.队列的实现
初始化队列
队尾入队列
队头出队列
获取队列队头元素
获取队列队尾元素
获取队列中有效元素个数
检测队列是否为空,如果为空返回非零结果,如果非空返回0
销毁队列
最后
前言
本篇文章内容讲述了栈和队列的概念结构、分类与函数声明部分,以及对于各个函数的实现。
以下内容仅供参考,欢迎各位大佬批评指正呦~
提示:以下是本篇文章正文内容,下面案例可供参考

一、栈
1.栈的概念及结构
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端 称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。 压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。 出栈:栈的删除操作叫做出栈。出数据也在栈顶。
2.栈的实现
栈的实现一般可以使用数组或者链表实现,相对而言数组的结构实现更优一些。因为数组在尾上插入数据的 代价比较小。
// 下面是定长的静态栈的结构,实际中一般不实用,所以我们主要实现下面的支持动态增长的栈
typedef int STDataType;
#define N 10
typedef struct Stack
{STDataType a[N];int _top; // 栈顶
}ST;// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{STDataType* a;int top; // 栈顶int capacity; // 容量
}ST;// 初始化栈
void StackInit(ST* ps); // 入栈
void StackPush(ST* ps, STDataType x); // 出栈
void StackPop(ST* ps); // 获取栈顶元素
STDataType StackTop(ST* ps); // 获取栈中有效元素个数
int StackSize(ST* ps); // 检测栈是否为空,如果为空返回非零结果,如果不为空返回0
int StackEmpty(ST* ps); // 销毁栈
void StackDestroy(ST* ps); 初始化栈
void StackInit(ST* ps) {assert(ps);ps->a = (STDatatype)malloc(sizeof(STDatatype) * 4);if (ps->a == NULL){perror("malloc fail");exit(-1);}ps->top = 0;ps->capacity = 4; }
入栈
void StackPush(ST* ps, STDatatype x) {assert(ps);if (ps->top == ps->capacity){STDatatype* tmp = (STDatatype*)realloc(ps->a,ps->capacity*2*sizeof(STDatatype));if (tmp == NULL){perror("realloc fail");exit(-1);}ps->a = tmp;ps->capacity *= 2;}ps->a[ps->top] = x;ps->top++;}
出栈
void StackPop(ST* ps) {assert(ps);assert(!StackEmpty(ps));ps->top--; }
获取栈顶元素
STDatatype StackTop(ST* ps) {assert(ps);assert(!StackEmpty(ps));return ps->a[ps->top - 1]; }
获取栈中有效元素个数
int StackSize(ST* ps) {assert(ps);return ps->top; }
检测栈是否为空,如果为空返回非零结果,如果不为空返回0
bool StackEmpty(ST* ps) {assert(ps);return ps->top == 0; }
销毁栈
void StackDestory(ST* ps) {assert(ps);free(ps->a);ps->a = NULL;ps->top = ps->capacity = 0; }
二、队列
1.队列的概念及结构
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出 FIFO(First In First Out) 入队列:进行插入操作的一端称为队尾 出队列:进行删除操作的一端称为队头
2.队列的实现
队列也可以数组和链表的结构实现,使用链表的结构实现更优一些,因为如果使用数组的结构,出队列在数 组头上出数据,效率会比较低。
// 链式结构:表示队列
typedef int QDataType;
typedef struct QueueNode
{QDataType data;struct QueueNode* next;
}QNode;// 队列的结构
typedef struct Queue
{ QNode* head;QNode* tail;int size;
}Queue; // 初始化队列
void QueueInit(Queue* pq); // 队尾入队列
void QueuePush(Queue* pq, QDataType data); // 队头出队列
void QueuePop(Queue* pq); // 获取队列头部元素
QDataType QueueFront(Queue* pq); // 获取队列队尾元素
QDataType QueueBack(Queue* pq); // 获取队列中有效元素个数
int QueueSize(Queue* pq); // 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* pq); // 销毁队列
void QueueDestroy(Queue* pq);初始化队列
void QueueInit(Queue* pq) {assert(pq);pq->head = NULL;pq->tail = NULL;pq->size = 0; }
队尾入队列
void QueuePush(Queue* pq, QDataType x) {assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->data = x;newnode->next = NULL;if (pq->tail == NULL){pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}pq->size++; }
队头出队列
void QueuePop(Queue* pq) {assert(pq);assert(!QueueEmpty(pq));if (pq->head->next == NULL){free(pq->head);pq->head = pq->tail = NULL;}else{QNode* del = pq->head;pq->head = pq->head->next;free(del);}pq->size--; }
获取队列队头元素
QDataType QueueFront(Queue* pq) {assert(pq);assert(!QueueEmpty(pq));return pq->head->data; }
获取队列队尾元素
QDataType QueueBack(Queue* pq) {assert(pq);assert(!QueueEmpty(pq));return pq->tail->data; }
获取队列中有效元素个数
int QueueSize(Queue* pq) {assert(pq);return pq->size; }
检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool QueueEmpty(Queue* pq) {assert(pq);return pq->head == NULL && pq->tail == NULL; }
销毁队列
void QueueDestroy(Queue* pq) {assert(pq);QNode* cur = pq->head;while (cur){QNode* del = cur;cur = cur->next;free(del);//del = NULL;}pq->head = pq->tail = NULL;pq->size = 0; }
最后
快乐的时光总是短暂的,以上就是今天要讲的内容,本文介绍了小赵同志对算法与数据结构(C语言)的栈和队列的初步认知以及实现。欢迎家人们批评指正。小赵同志继续更新,不断学习的动力是宝子们一键三连的支持呀~

相关文章:

【算法与数据结构(C语言)】栈和队列
文章目录 目录 前言 一、栈 1.栈的概念及结构 2.栈的实现 入栈 出栈 获取栈顶元素 获取栈中有效元素个数 检测栈是否为空,如果为空返回非零结果,如果不为空返回0 销毁栈 二、队列 1.队列的概念及结构 2.队列的实现 初始化队列 队尾入队列 队头出队列 获…...
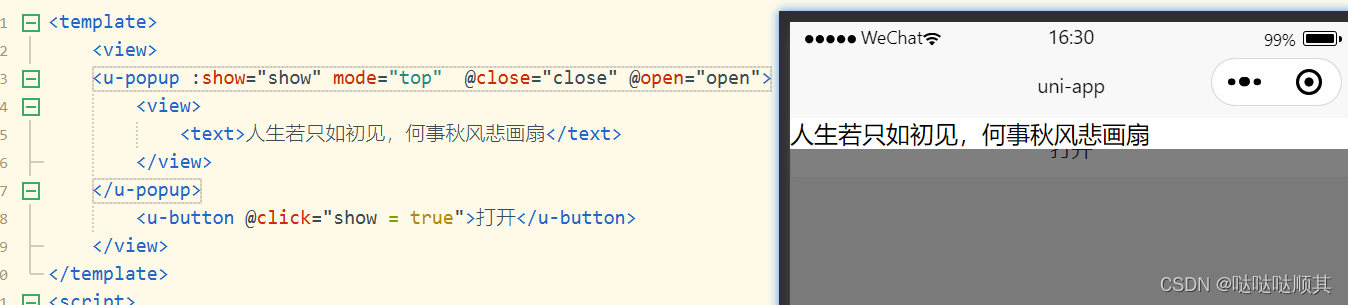
Uni-app使用vant和uview组件
目录 1.安装vant组件 1.1安装前需知 1.2.安装 1.3.创建uni-app项目 2.安装uview-ui组件 2.1官网 2.2安装 2.3安装成功 1.安装vant组件 1.1安装前需知 小程序能使用vant-weapp组件,且官网的安装是直接导入小程序中,不能直接导入uni-app框架中 V…...
2023年PMP考试应该注意些什么?
首先注意(报考条件) 2023年PMP考试报名流程: 一、PMP英文报名: 英文报名时间无限制,随时可以报名,但有一年的有效期,所以大家尽量提前报名,在英文报名有效期内进行中文报名。 英…...
selenium环境安装及使用
selenium简介官网https://www.selenium.dev简介用于web浏览器测试的工具支持的浏览器包括IE,Firefox,Chrome,edge等使用简单,可使用java,python等多种语言编写用例脚本主要由三个工具构成,webdriver,IDE,web自动化环境…...
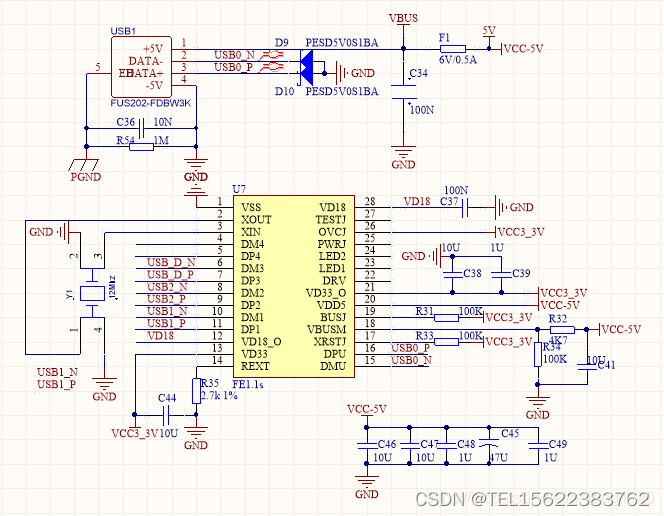
高性能低功耗4口高速USB2.0 HUB 完美替代FE1.1S和FE8.1
该NS1.1s是一个高度集成的,高品质,高性能,低功耗,为USB 2.0高速4端口集线器又低成本的解决方案。 (点击即可咨询芯片详细信息) NS1.1s的特点 1.通用串行总线规范修订版2.0(USB 2.0)完…...
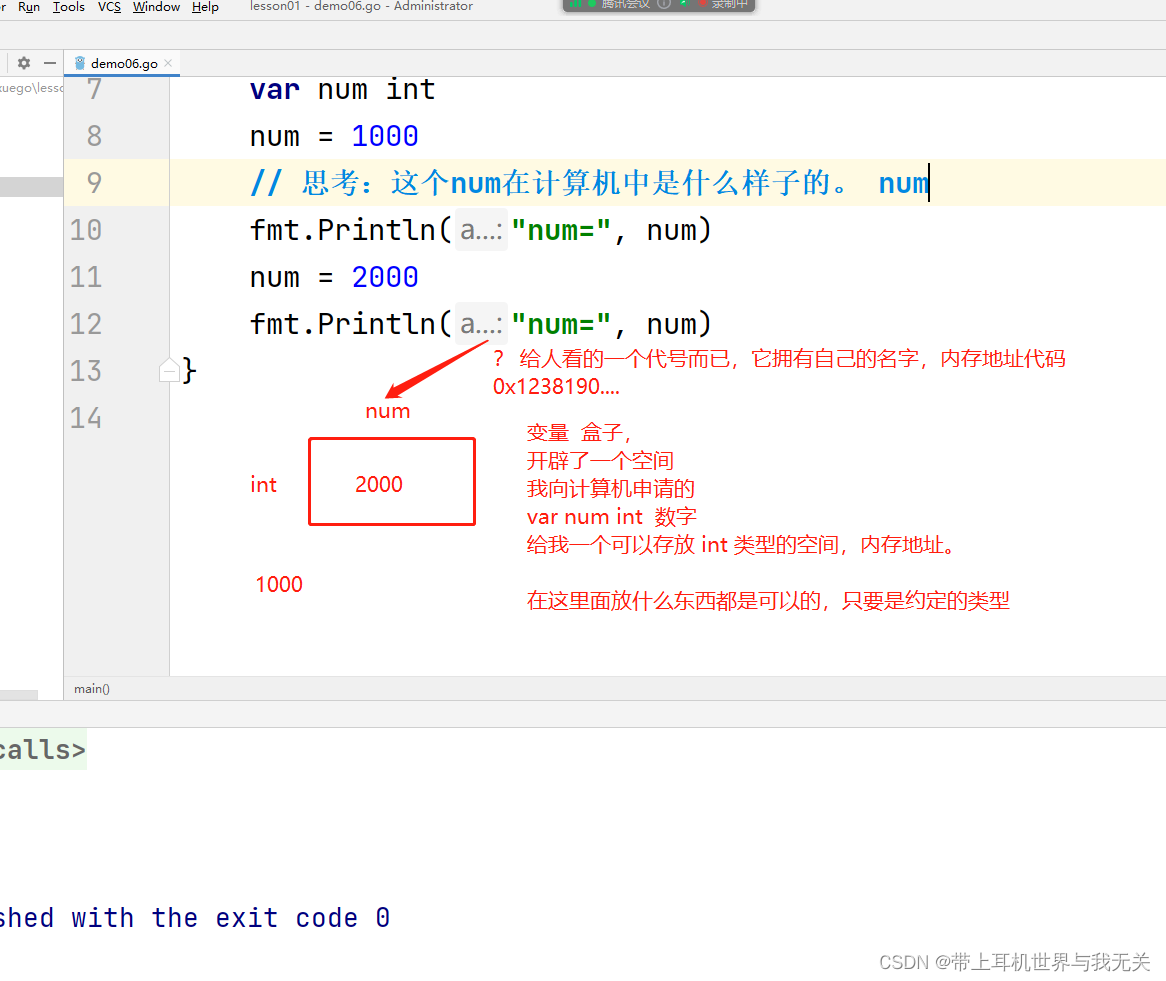
Go全栈学习(一)基础语法
Go语言基础语法 文章目录Go语言基础语法注释变量变量的定义变量的交换理解变量(内存地址)匿名变量变量的作用域常量2023.2.4日 总结// 关于Goland 中 执行的问题// 1、包下执行 (一个 main 函数来执行,如果有多个,无法…...
centos7搭建svn配置
基本概述 Apache Subversion(简称SVN,svn),一个开放源代码的版本控制系统,相较于RCS、CVS,它采用了分支管理系统,它的设计目标就是取代CVS。互联网上很多版本控制服务已从CVS转移到Subversion。…...
趣味三角——第12章——tanx
第12章节 tanx In his very numerous memoires, and especially in his great work, Introductio in analysin infinitorum (1748), Euler displayed the most wonderful skill in obtaining a rich harvest of results of great interest. . . . Hardly any other work …...
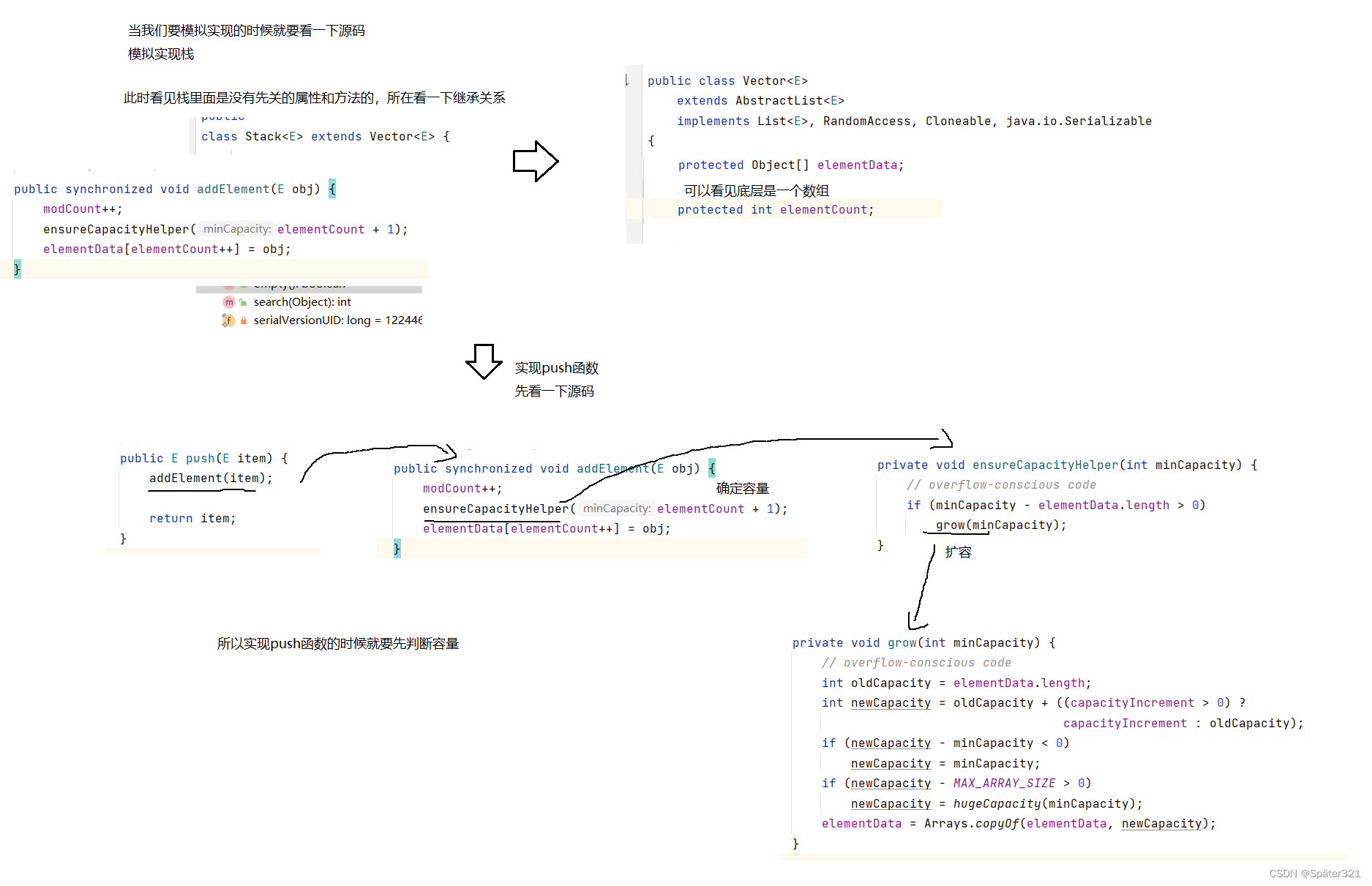
Java - 数据结构,栈
一、栈 1.1、什么是栈 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈 顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。 压…...
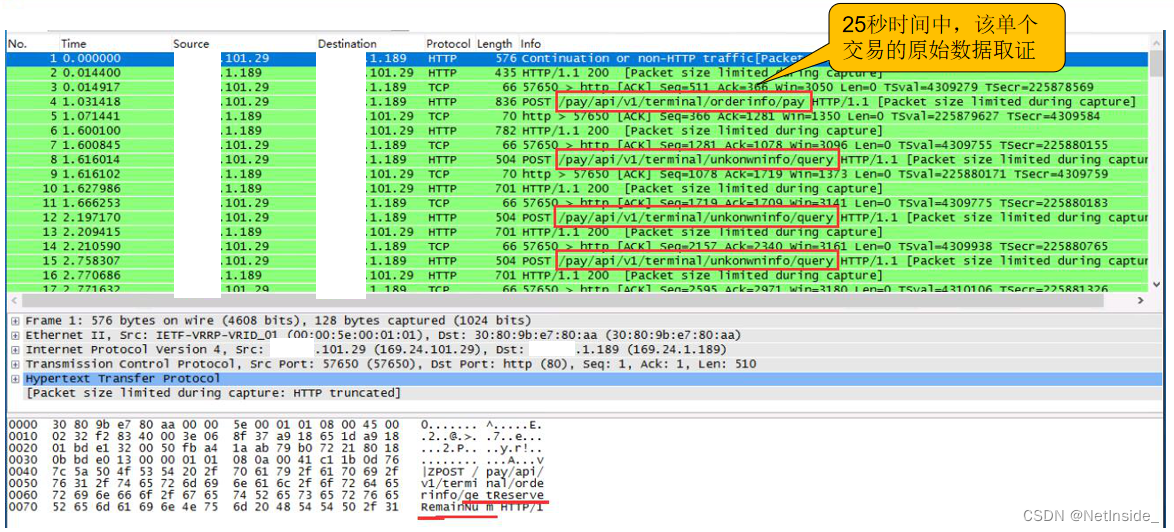
某餐厅系统网络故障分析案例
背景 针对食堂经营企业,某堂食软件为客户提供优化堂食就餐流程、提高食堂服务水平和管理效率。 某上海客户使用该堂食系统,在就餐高峰时段,总是出现支付、点餐等操作缓慢,动辄一个操作需要等待几十秒。该客户联系软件厂商&#…...

华为OD机试题,用 Java 解【密室逃生游戏】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...

如何重命名SQL Server数据库
重命名SQL Server数据库 使用T-SQL重命名SQL Server数据库使用分离和附加重命名SQL Server数据库使用T-SQL查询分离和重新连接在SSMS中分离和重新连接通过SSMS重命名SQL Server数据库当使用SQL数据库很长一段时间时,你可能会遇到需要为数据库命名的情况。它可以用几种不同的方…...

联想昭阳E5-ITL电脑开机后绿屏怎么U盘重装系统?
联想昭阳E5-ITL电脑开机后绿屏怎么U盘重装系统?有用户电脑正常开机之后,出现了屏幕变成绿屏,无法进行操作的情况。这个问题是系统出现了问题,那么如何去进行问题的解决呢?接下来我们一起来分享看看如何使用U盘重装电脑…...
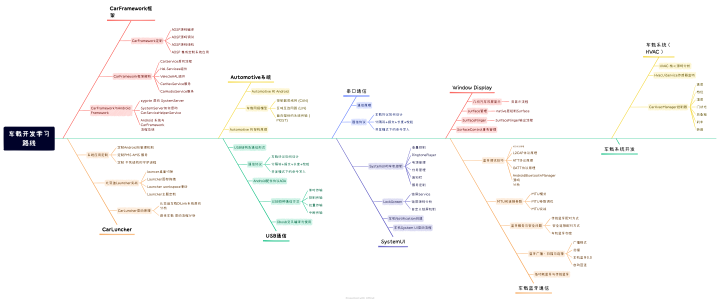
车载开发知识交流【学习路线】
前言 在2023国内百废待兴;经济复苏的号召一直在响应,这对于压抑了三年的人民来说无疑是福音。这篇我们主要说一下拉动经济的其中大板块——车企;我们知道我们最大的经济除了房地产,第二就是车企。而在造车领域中也不断的加入了许…...

【读书笔记】《深入浅出数据分析》第二章 检验你的理论
文章目录一,相关分析方法1,相关系数二,相关性不等于因果关系三,证明因果关系,“控制变量法”?本章主要说明了两个问题: 1,相关性不等于因果关系 2,如何判断两种数据之间是相关性&am…...
:table_apisql)
pyflink学习笔记(一):table_apisql
具体定义请参考官方文档:https://nightlies.apache.org/flink/flink-docs-release-1.16/zh/docs/dev/table/overview/本文主要针对实际使用中比较常用的api进行整理,大多数例子都是官网,如有歧义可与官方对照。一、 创建 TableEnvironmentTab…...

GCC 编译器套件说明
写在前面: 本文章旨在总结备份、方便以后查询,由于是个人总结,如有不对,欢迎指正;另外,内容大部分来自网络、书籍、和各类手册,如若侵权请告知,马上删帖致歉。 目录GCC 简述GCC 主要…...
IDEA集成Git
1:IDEA集合Git1.1:配置Git忽略文件-IDEA特定文件问题 1:为什么要忽略他们?答: 与项目的实际功能无关, 不参与服务器上部署运行。把它们忽略掉能够屏蔽 IDE 工具之间的差异。问题 2:怎么忽略?1&a…...

算法流程图
里程计定位: 优:定位信息连续,无离散的跳跃 缺:存在累计误差,不利于长距或长期定位 传感器定位: 优:比里程计定位更精准 缺:会出现跳变情况,且传感器定位在标志物较少的环…...
Java中安装JDK环境–javac命令无效
Java中安装JDK环境–javac命令无效 一,安装JDK1.8 阿里云盘地址推荐 我们可以选择安装地址,这个地址是我们用来配置环境变量的,唯一注意的是这个,其他的都是默认下一步。直至安装完成,jdk下载地址https://www.oracl…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
