【读书笔记】《深入浅出数据分析》第二章 检验你的理论
文章目录
- 一,相关分析方法
- 1,相关系数
- 二,相关性不等于因果关系
- 三,证明因果关系,“控制变量法”?
本章主要说明了两个问题:
1,相关性不等于因果关系
2,如何判断两种数据之间是相关性,还是因果关系?
一,相关分析方法
当研究两种或两种以上的数据之间有什么关系时,就要用到相关分析,如果两种数据之间有关系,叫作有相关关系,否则没有相关关系。
1,相关系数
相关系数可以用来衡量两种数据之间的相关程度。
(1)相关系数的数值大小可以表示两种数据的相关程度。
(2)相关系数的正负可以表示表示两种数据的相关方向。
当两个或两个以上的变量变化方向相同,正相关,相关系数>0。例如,夏天温度越高,冰淇淋销量越高。
当两个或两个以上的变量变化方向相反,负相关,相关系数<0。例如,速度与时间。
当两个或两个以上的变量变没有相关性,相关系数=0。
在分析过程中,相关分析可以帮助发现事物之间的联系。在某些情况下,甚至可以识别数据之间的因果关系。例如,温度越高,融化越快,但是,在得出这种结论时,我们必须小心谨慎。因果关系蕴藏着相关关系,但相关关系不等于因果关系。如果我们曲解了相关关系,我们就可能陷入错误的原因谬论。
二,相关性不等于因果关系
如果A和B存在正相关,A提升,B也提升,但是我们却不能简单地认为:B提升的原因是A提升,实际上,可能存在两种可能:
(1)纯属巧合。
(2)存在第三个变量C影响着B。
例如,冰激凌销量增加导致溺水事故增多
真相是,冰淇凌销量增加(A)和溺水事故增多(B)的关系,A和B有一个共同原因就是(夏天高气温),且A和B在统计学中曲线高度一致(具有相关性),但我们却不能想当然的定义A导致B,或B导致A(因果性)。
关于相关性和因果关系的深入探讨:https://www.cnblogs.com/LittleHann/p/12463465.html#_lab2_2_1
三,证明因果关系,“控制变量法”?
在自然科学常使用到一种实验方法:“控制变量法”,借用Wiki的术语,控制变量法通常称为Scientific Control,即在实验设计上,保证实验组和对照组之间只存在一个变量影响两组之间实验结果的差异。设置对照的目的通常是为了消除其他混杂因素对于实验结果的影响。对比实验组和对照组的结果,如果结果有任何的不同,都可以归因于这个变量。这些实验背后都有物理、化学、数学等基础原理支撑的,这些原理是稳定、科学、可量化的,因此可以通过数据统计+科学实验,慢慢地发现背后的自然规律。
然而,在实际分析工作中,这套方法可能不是很适用,因为其中会有很多混杂因素的影响,这些混杂因素无法被完全消除,比如,在营销、运营、产品、销售领域,无法完全消除人主观因素的影响,所以大多时候,无法找到其中的因果关系,但知道相关关系就可以帮助我们。
比如,大数据的经典案例之一是“啤酒和尿布”的故事,沃尔玛超市通过大量的数据,通过购物篮分析发现,买啤酒的人也买尿布,于是在货物架上,把两者放一块了,结果大大提升了销售额。这个很难证明其中的因果关系,但是只要运用啤酒和尿布的相关性,就可以提高销售额。

再比如,某宝,某东,给我们推荐商品,背后都是对我们的行为进行相关性分析,为我们推荐感兴趣的商品,从而提高销售额。
相关文章:

【读书笔记】《深入浅出数据分析》第二章 检验你的理论
文章目录一,相关分析方法1,相关系数二,相关性不等于因果关系三,证明因果关系,“控制变量法”?本章主要说明了两个问题: 1,相关性不等于因果关系 2,如何判断两种数据之间是相关性&am…...
:table_apisql)
pyflink学习笔记(一):table_apisql
具体定义请参考官方文档:https://nightlies.apache.org/flink/flink-docs-release-1.16/zh/docs/dev/table/overview/本文主要针对实际使用中比较常用的api进行整理,大多数例子都是官网,如有歧义可与官方对照。一、 创建 TableEnvironmentTab…...

GCC 编译器套件说明
写在前面: 本文章旨在总结备份、方便以后查询,由于是个人总结,如有不对,欢迎指正;另外,内容大部分来自网络、书籍、和各类手册,如若侵权请告知,马上删帖致歉。 目录GCC 简述GCC 主要…...
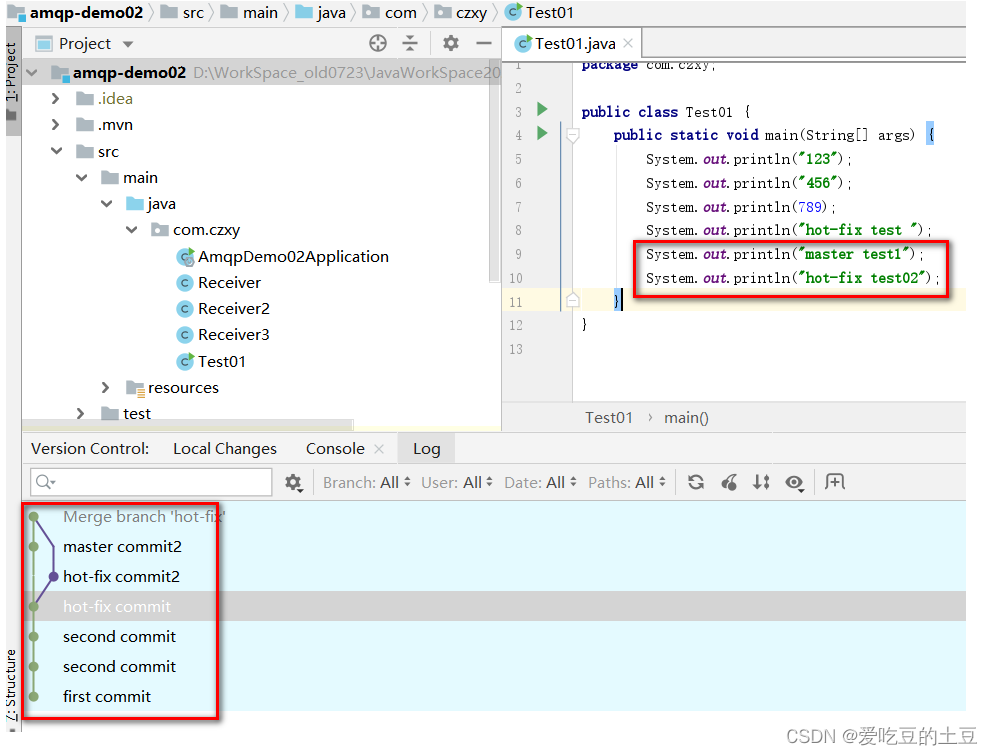
IDEA集成Git
1:IDEA集合Git1.1:配置Git忽略文件-IDEA特定文件问题 1:为什么要忽略他们?答: 与项目的实际功能无关, 不参与服务器上部署运行。把它们忽略掉能够屏蔽 IDE 工具之间的差异。问题 2:怎么忽略?1&a…...

算法流程图
里程计定位: 优:定位信息连续,无离散的跳跃 缺:存在累计误差,不利于长距或长期定位 传感器定位: 优:比里程计定位更精准 缺:会出现跳变情况,且传感器定位在标志物较少的环…...
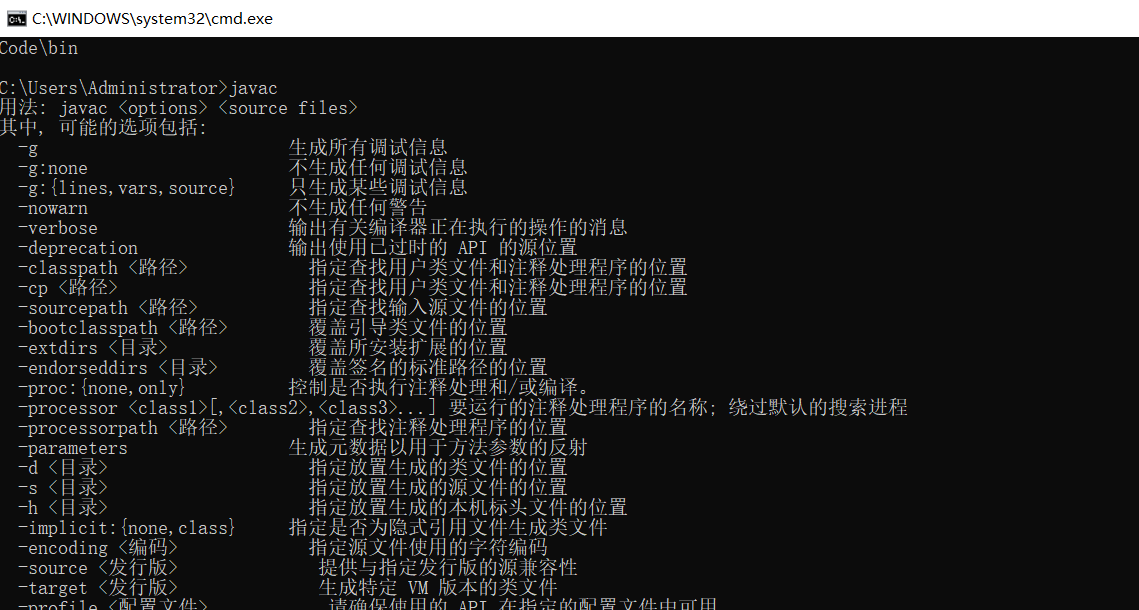
Java中安装JDK环境–javac命令无效
Java中安装JDK环境–javac命令无效 一,安装JDK1.8 阿里云盘地址推荐 我们可以选择安装地址,这个地址是我们用来配置环境变量的,唯一注意的是这个,其他的都是默认下一步。直至安装完成,jdk下载地址https://www.oracl…...

递推问题
递推:在面对一个大任务的时候,有时候我们可以将大任务划分为小任务,再将小任务划分为更小的任务......,直到遇到初始情况,最后由初始情况一直往前推进,最后解决大任务,这就是递推的思想。递推问…...

js中强制类型转换Number、parseInt、parseFloat、Boolean、String、toString的使用
文章目录一、Number() 转换为整数二、Number.parseInt() 将字符串转换为整数三、Number.parseFloat() 将字符串转换为浮点数四、Boolean() 转换为布尔值五、String() 转换为字符串六、.toString() 转换为字符串最近在巩固 js 的基础知识,今天复习到了 js 中的数据类…...
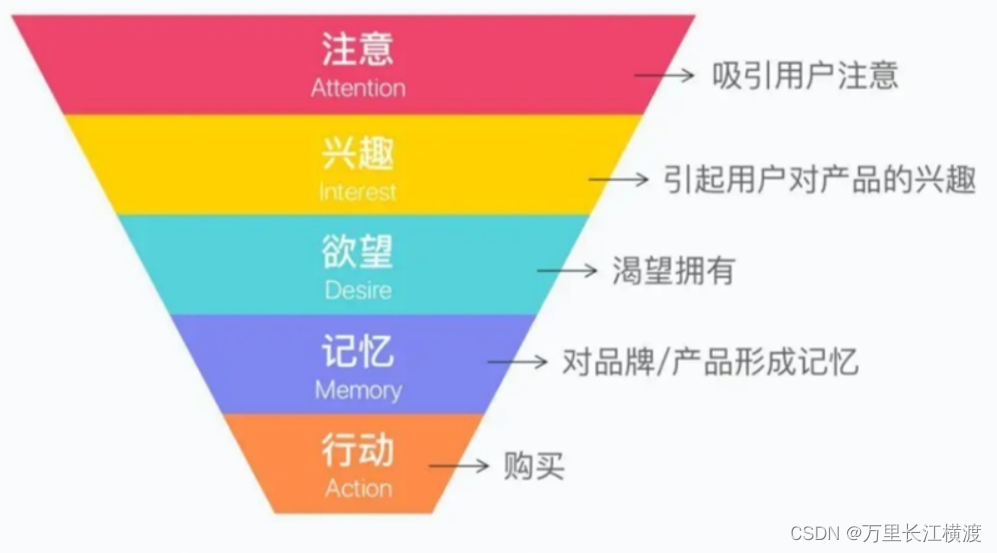
漏斗分析法
一什么是漏斗分析? 漏斗分析是数据领域最常见的一种“程式化”数据分析方法,它能够科学地评估一种业务过程,从起点到终点,各个阶段的转化情况。通过可以量化的数据分析,帮助业务找到有问题的业务环节,并进…...
)
pycharm入门快捷操作(部分)
altenter:提示意图动作shift两次或者crtlshifta:查找框(查找动作、类、项目等)crtlw:一次一个字符、两次整个字符串(if条件下选择整个判断体)、三次整个句子、四次整个引用ctrlshiftw࿱…...

宣布 Databricks 支持 Amazon Graviton2,性价比提高3倍
今天,我们很高兴地宣布 Databricks 对基于 Amazon Graviton2 的亚马逊弹性计算云(Amazon EC2)实例的支持的公开预览。Graviton 处理器由亚马逊云科技进行定制设计和优化,为运行在 Amazon EC2 上的云工作负载提供最佳性价比。当与高…...
18_FreeRTOS任务通知
目录 任务通知的简介 任务通知值的更新方式 任务通知的优势 任务通知的劣势 任务通知值和通知状态 发送通知相关API函数 接收通知相关API函数 任务通知模拟信号量实验 任务通知模拟消息邮箱实验 任务通知模拟事件标志组实验 任务通知的简介 任务通知:用来通知任务的…...

【华为OD机试模拟题】用 C++ 实现 - 整理扑克牌(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...
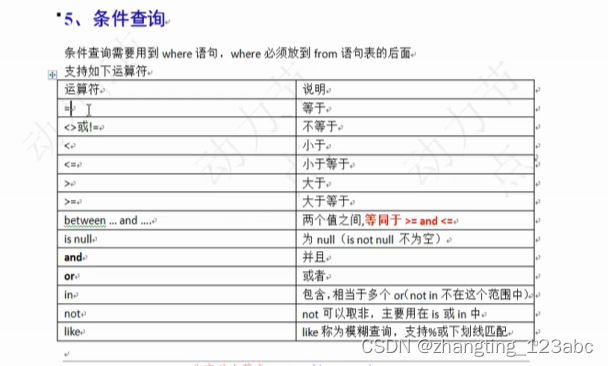
mysql lesson1
常用命令 1:exit 退出mysql 2:uroot pENTER键,再输入密码,不被别人看见 3:完美卸载:双击安装包,手动删除program file中的mysql,手动删除Programedate里的mysql 4:use mysql 使用数据库 5:…...
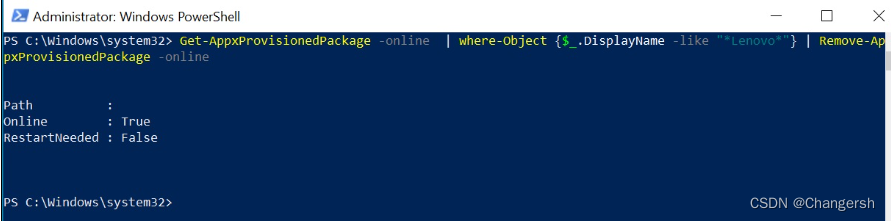
联想笔记本无法下载 Lenovo Vantage
状况 在 Microsoft Store 下载时发生错误,可能是如下代码:0x80070005, 0x80073D05, or 0x80070017. 解决方法 1.在“开始”菜单搜索栏中输入PowerShell 2.当Windows PowerShell出现在“开始”菜单中,右键点击此图标,然后选择以…...

功能性材料深入超级赛道,赋能多行业迭代升级
中国国际胶粘剂及密封剂展览会深耕胶粘剂、密封剂和胶粘带行业26年,是行业认可的、优质的贸易与技术交流平台。展会连接了十几个行业的买家和卖家,包括汽车、电子、新能源、轨道交通、工业等重要领域,为客户提供封装、粘合、散热、装配制造等…...

【项目精选】jsp企业快信系统(论文+视频+源码)
点击下载源码 计算机网络的出现到现在已经经历了翻天覆地的重大改变。因特网也从最早的供科学家交流心得的简单的文本浏览器发展成为了商务和信息的中心。到了今天,互联网已经成为了大量应用的首选平台,人们已经渐渐习惯了网络交易,渐渐对网络…...

通信算法之112:载波同步及comm.CarrierSynchronizer
1. 2. 载波同步是基于锁相环技术使本地获取和载波同频同相的参考信号,用来解调信号。载波同步就是对本地参考信号进行频率和相位偏差的补偿,进而实现本地参考信号和载波信号同频同相。 载波同步只适用于单载波调制系统,载波同步算法对于BPSK、…...
)
【C. Build Permutation】(整数理论、构造、思维)
链接 理论基础 结论:在区间[n,2n]上,至少存在一个完全平方数。结论:在区间[n,2n]上,至少存在一个完全平方数。结论:在区间[n,2n]上,至少存在一个完全平方数。 构造⌈n⌉2构造\lceil \sqrt{n}\rceil^2构造⌈…...
)
前端面试题:事件循环(Eventloop)
什么是事件循环?如何理解事件循环?事件循环原理如何描述?事件循环涉及了很多知识点,想要彻底掌握JS事件循环原理必须要掌握以下知识点:同步任务、异步任务、宏任务、微任务、任务队列、执行栈、js运行机制、EventLoop。 1.事件循…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
