想要精通算法和SQL的成长之路 - 验证二叉搜索树和不同的二叉搜索树
想要精通算法和SQL的成长之路 - 验证二叉搜索树和不同的二叉搜索树
- 前言
- 一. 验证二叉搜索树
- 二. 不同的二叉搜索树
- 三. 不同的二叉搜索树II
前言
想要精通算法和SQL的成长之路 - 系列导航
二叉搜索树的定义:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
一. 验证二叉搜索树
原题链接

思路:
- 树的中序遍历:左节点 --> 父节点 --> 右节点。
- 我们按照中序遍历二叉树,比较节点的大小即可。可以用一个全局的临时变量来存储上一个节点的值。
代码如下:
long preVal = Long.MIN_VALUE;public boolean isValidBST(TreeNode root) {if (root == null) {return true;}// 判断左节点if (!isValidBST(root.left)) {return false;}// 当前节点肯定是要大于上一个节点的值的,这样才满足二叉搜索树的性质if (root.val <= preVal) {return false;}// 更新pre值preVal = root.val;// 判断右节点return isValidBST(root.right);
}
二. 不同的二叉搜索树
原题链接
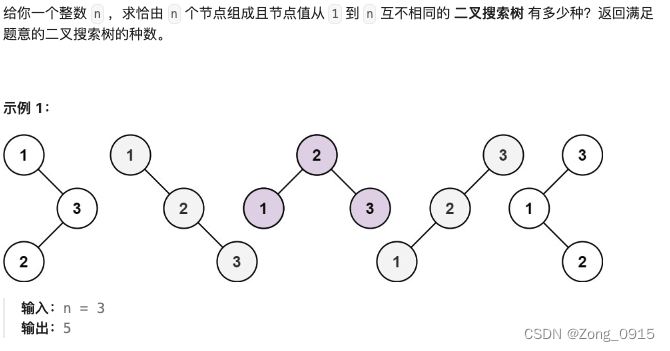
思路如下:
- 我们假设
dp[i]是以i个数字组合而成的不同二叉搜索树的个数。 f(i):代表以数字i为根节点的二叉搜索树个数。- 那么此时,左节点的节点数量为:
i - 1,右节点的节点数量为:n - i。那么左侧节点可组成的不同二叉树个数为:dp[i-1],右侧为:dp[n-i]。 - 即
f(i) = dp[i-1] * dp[n-i]。 - 而
dp[n] = f(1) + f(2) + ... + f(n) = dp[0] * dp[n-1] + dp[1] * dp[n-2] + ... + dp[n-1] + dp[0]。即得一个动态规划的递推公式。
最终代码如下:
public int numTrees(int n) {int[] dp = new int[n + 1];// 初始化dp[0] = 1;dp[1] = 1;for (int i = 2; i < n + 1; i++) {for (int j = 1; j < i + 1; j++) {dp[i] += dp[j - 1] * dp[i - j];}}return dp[n];
}
三. 不同的二叉搜索树II
原题链接
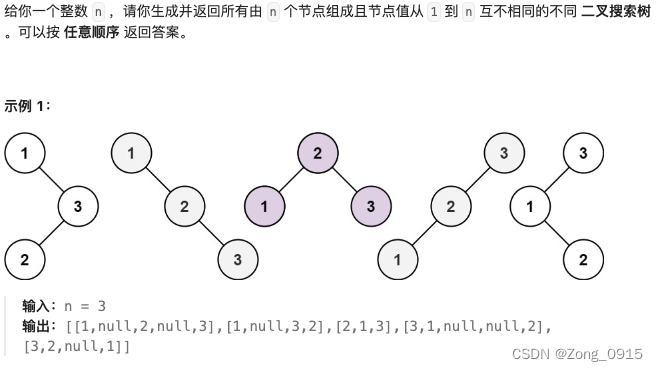
我们可以用自底向上的一种思路去考虑,当以数字 i 作为根节点,构建二叉搜索树的时候,数量有多少?
- 我们假设一个函数:
buildTree(int left , int right)是用来统计区间[left,right]范围内,不同的二叉搜索树集合。
- 那么当以数字
i作为根节点的时候,左侧区间可拿到的集合为:buildTree(left, i -1 ),右侧为:buildTree(i+1,right)。 - 拿到这两个左右集合之后,我们遍历他们,两两结合,以数字 i 作为根节点,构建二叉搜索树。
不难得出代码:
public List<TreeNode> buildTree(int left, int right) {ArrayList<TreeNode> res = new ArrayList<>();// 边界判断if (left > right) {res.add(null);return res;}if (left == right) {res.add(new TreeNode(left));return res;}// 统计区间[left,right]内的二叉搜索树个数for (int i = left; i <= right; i++) {// 如果以 i 作为二叉搜索树的根节点,那么,左侧区间可构建的二叉搜索树的数量为List<TreeNode> leftBSTNum = buildTree(left, i - 1);List<TreeNode> rightBSTNum = buildTree(i + 1, right);// 左右两个子二叉搜索树两两结合for (TreeNode leftTree : leftBSTNum) {for (TreeNode rightTree : rightBSTNum) {TreeNode root = new TreeNode(i);root.left = leftTree;root.right = rightTree;res.add(root);}}}return res;
}
那么最终代码如下:
public List<TreeNode> generateTrees(int n) {ArrayList<TreeNode> res = new ArrayList<>();// 特殊值判断if (n == 0) {return res;}return buildTree(1, n);
}public List<TreeNode> buildTree(int left, int right) {ArrayList<TreeNode> res = new ArrayList<>();// 边界判断if (left > right) {res.add(null);return res;}if (left == right) {res.add(new TreeNode(left));return res;}// 统计区间[left,right]内的二叉搜索树个数for (int i = left; i <= right; i++) {// 如果以 i 作为二叉搜索树的根节点,那么,左侧区间可构建的二叉搜索树的数量为List<TreeNode> leftBSTNum = buildTree(left, i - 1);List<TreeNode> rightBSTNum = buildTree(i + 1, right);// 左右两个子二叉搜索树两两结合for (TreeNode leftTree : leftBSTNum) {for (TreeNode rightTree : rightBSTNum) {TreeNode root = new TreeNode(i);root.left = leftTree;root.right = rightTree;res.add(root);}}}return res;
}
相关文章:

想要精通算法和SQL的成长之路 - 验证二叉搜索树和不同的二叉搜索树
想要精通算法和SQL的成长之路 - 验证二叉搜索树和不同的二叉搜索树 前言一. 验证二叉搜索树二. 不同的二叉搜索树三. 不同的二叉搜索树II 前言 想要精通算法和SQL的成长之路 - 系列导航 二叉搜索树的定义: 节点的左子树只包含 小于 当前节点的数。节点的右子树只包…...
SpringCloudAlibaba 相关组件的学习一
目录 前言 系统架构演变 1、单体架构 2、垂直架构 3、分布式架构 4、SOA架构 5、微服务架构 一、微服务架构的介绍 1、微服务架构的常见问题 2 微服务架构的常见概念 2.1 服务治理 2.2 服务调用 2.3 服务网关 2.4 服务容错 2.5 链路追踪 3、微服务架构的常用解决…...

【C语言 模拟实现strncpy函数、strncat函数、strncmp函数、strstr函数】
C语言程序设计笔记---026 C语言之模拟实现strncpy函数、strncat函数、strncmp函数、strstr函数1、介绍strncpy函数1.1、模拟实现strncpy函数 2、介绍strncat函数2.1、模拟实现strncat函数 3、介绍strncmp函数3.1、模拟实现strncmp函数 4、介绍strstr函数4.1、模拟实现strstr函数…...

Mongodb7启动报错排除解决方案
一: 报错信息: [rootwww log]# journalctl -xe -- Unit mongodb.service has begun starting up. /usr/local/mongodb/mongdb7/bin/mongod --help for more information 10月 03 13:47:39 www.yhchange.com systemd[1]: mongodb.service: control process exited, …...

王杰国庆作业day5
...
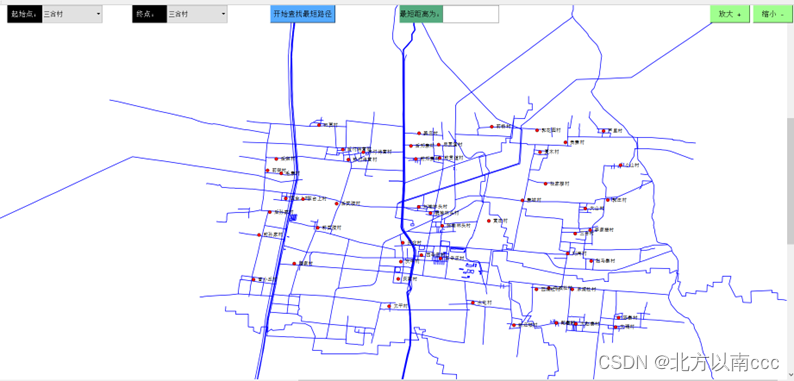
QT、C++实现地图导航系统(mapSystem)
文章目录 地图导航系统项目应用背景技术栈选择数据处理算法实现界面实现源码展示成果展示源码下载 (免费) 地图导航系统 项目应用背景 电子地图导航系统的主要目的是为用户提供精确、实时的导航和位置信息,以帮助他们在城市或地区内轻松找到…...

STM32 定时器介绍--通用、高级定时器
目录 高级定时器 1.功能框图 1-时钟源 2-时基单元 3-输入捕获 4-输出比较 2.输入捕获的应用 3.输出比较的应用 4.初始化结构体 1-时基初始化结构体 2-输出比较结构体 3-PWM信号 周期和占空比的计算--以通用定时器为例 4-输入捕获结构体 5-断路和死区初始化结构体…...
淘宝天猫渠道会员购是什么意思?如何开通天猫淘宝渠道会员购有什么用?
淘宝天猫渠道会员购是什么意思? 淘宝天猫渠道会员购与淘宝天猫粉丝福利购意思基本相同,都可以领取淘宝天猫大额内部隐藏优惠券、通过草柴APP开通绑定渠道会员还可以获得购物返利。 草柴APP如何绑定开通淘宝天猫渠道会员? 1、手机下载安装「…...
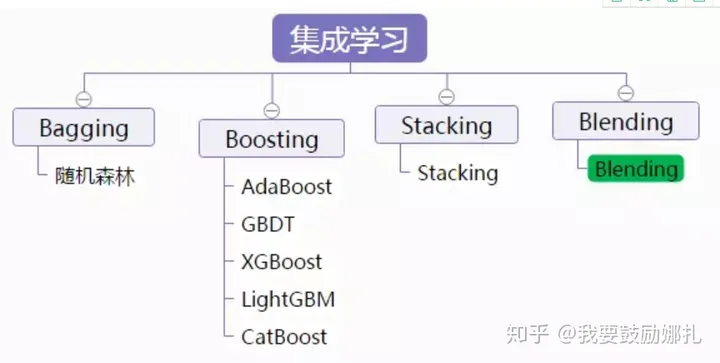
(Note)机器学习面试题
机器学习 1.两位同事从上海出发前往深圳出差,他们在不同时间出发,搭乘的交通工具也不同,能准确描述两者“上海到深圳”距离差别的是: A.欧式距离 B.余弦距离 C.曼哈顿距离 D.切比雪夫距离 S:D 1. 欧几里得距离 计算公式&#x…...

思科:iOS和iOSXe软件存在漏洞
思科警告说,有人试图利用iOS软件和iOSXe软件中的一个安全缺陷,这些缺陷可能会让一个经过认证的远程攻击者在受影响的系统上实现远程代码执行。 中严重程度的脆弱性被追踪为 CVE-2023-20109 ,并以6.6分得分。它会影响启用Gdoi或G-Ikev2协议的软件的所有版本。 国际知名白帽黑客…...

CCF CSP认证 历年题目自练Day19
题目一 试题编号: 201812-1 试题名称: 小明上学 时间限制: 1.0s 内存限制: 512.0MB 问题描述: 题目背景 小明是汉东省政法大学附属中学的一名学生,他每天都要骑自行车往返于家和学校。为了能尽可能充…...

Java 开发环境配置
在本章节中我们将为大家介绍如何搭建Java开发环境。 目录 window系统安装java 下载JDK 配置环境变量 JAVA_HOME 设置 PATH设置 CLASSPATH 设置 测试JDK是否安装成功 Linux,UNIX,Solaris,FreeBSD环境变量设置 流行 Java 开发工具 使…...

[2023.09.26]: JsValue的转换体验与as关键字的浅析
昨天解决了焦点问题,今天就开始搬砖了。本以为可以一帆风顺,但是还是遇到了几个问题,不过还好,都被一一解决,这里我分享一下JsValue的转换体验以及关键字as的使用浅析。 场景描述 我是在什么情况下遇到JsValue的转换…...
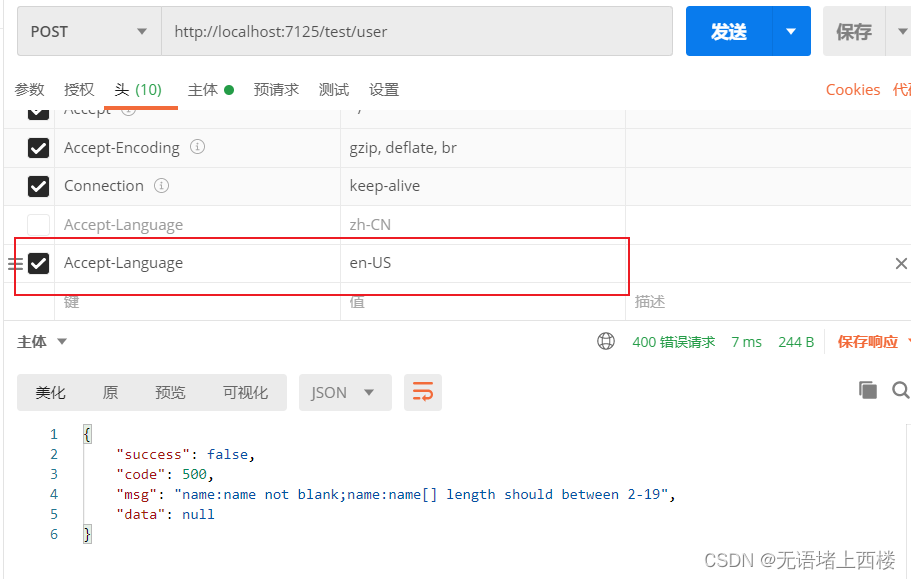
SpringBoot Validation入参校验国际化
在 Spring Boot 中,可以使用 Validation 和国际化来实现对入参的校验。 常用的校验 NotNull验证字段值不能为 nullNotEmpty验证字段值不能为 null 或空字符串NotBlank验证字符串字段值不能为空、null,并且必须至少包含一个非空白字符Size验证字符串、…...

树莓集团涉足直播产业园区运营,成都直播产业园区再添黑马
树莓集团涉足成都直播产业园运营领域,这一消息引起了业界的广泛关注。在这个无限可能的直播领域中,树莓集团将与上市公司德商产投紧密合作,立志为成都直播行业的发展注入新的活力。成都天府蜂巢直播产业园推行着一系列创新的政策措施…...

中小学教师ChatGPT的23种用法
原文:中小学教师ChatGPT的23种用法 近日,ChatGPT引发舆论风暴,火遍全球。作为一款生成式人工智能软件,ChatGPT可以就任何议题生成文本,完成包括回答问题,撰写文章、论文、诗歌在内的多种工作。各界盛赞其“…...
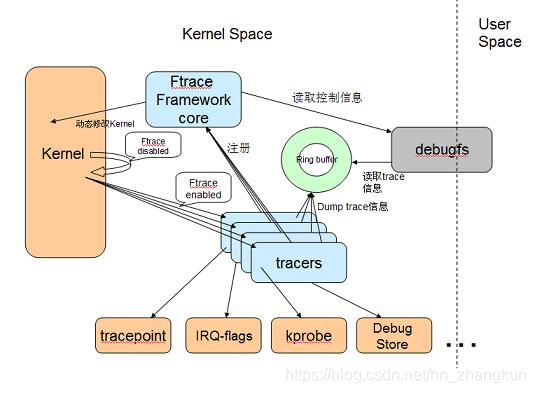
Ubuntu性能分析-ftrace 底层驱动
1、框架介绍 ftrace内核驱动可以分为几部分:ftrace framework,RingBuffer,debugfs,Tracepoint,各种Tracer。 ftrace框架是整个ftrace功能的纽带,包括对内和的修改,Tracer的注册,RingBuffer的控制等等。 RingBuffer是静态动态ftrace的载体。 debugfs则提供了用户空间…...

网盘搜索引擎:点亮知识星空,畅享数字宝藏!
大家好!作为一名资深的网络产品运营人员,我今天要向大家介绍一款让你受益匪浅的神奇工具——网盘搜索引擎!它可以帮助你免费搜索查询各种云盘共享资源,包括影视作品、纪录片、小说、动漫等等。现在,我们急需网络流量&a…...
Mysql以key-val存储、正常存储的区别
场景 你作为一个服务端工程师,假设产品要求设计这么一个页面,页面上包含很多模块,每个模块都可以单独进行变更,有些模块是富文本。 实现方式有很多,我们来聊比较常用的两种,看看mysql的表如何设计。 第一…...

MySQL 索引优化实践(单表)
目录 一、前言二、表数据准备三、常见业务无索引查询耗时测试3.1、通过订单ID / 订单编号 查询指定订单3.2、查询订单列表 四、订单常见业务索引优化实践4.1、通过唯一索引和普通索引优化通过订单编号查询订单信息4.2、通过普通联合索引优化订单列表查询4.2.1、分析查询字段的查…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...

MCP和Function Calling
MCP MCP(Model Context Protocol,模型上下文协议) ,2024年11月底,由 Anthropic 推出的一种开放标准,旨在统一大模型与外部数据源和工具之间的通信协议。MCP 的主要目的在于解决当前 AI 模型因数据孤岛限制而…...
