量子计算基础知识—Part1
1.什么是量子计算机?
量子计算机是基于量子力学原理构建的机器,采用了一种新的方法来处理信息,从而使其具有超强的功能。量子计算机使用Qubits处理信息。
2. 什么是量子系统?
一个量子系统指的是由量子力学规则描述和控制的物理系统。在量子力学中,物理系统的状态不再是经典物理中的确定性值,而是由一个称为波函数的数学对象描述的概率分布(粒子的状态不是确定的,而是以概率的形式存在。)。波函数可以用来计算量子系统在不同状态下的概率和测量结果。波函数告诉我们在不同状态下发现粒子的概率,例如它在某个位置的概率或具有某个能量的概率。
一个量子系统可以处于多个态的叠加状态,这与经典物理中的叠加不同。量子叠加的概念意味着在观测之前,系统可以同时处于多个可能的状态,并且这些状态之间会发生干涉。
量子系统的演化是通过薛定谔方程描述的,该方程描述了波函数随时间的变化。通过对量子系统的操作和测量,可以利用量子叠加和纠缠的性质来进行量子计算、量子通信和量子模拟等应用。
量子系统可以由一个或多个量子粒子组成,例如电子、光子或原子等。这些粒子的行为受到量子力学的规则和原理的约束,如叠加原理、量子纠缠和量子态的坍缩等。
2.1 密度矩阵
密度矩阵的引入是为了描述量子系统在纯态和混合态之间的过渡,以及处理涉及量子测量和量子统计的情况。在传统的量子力学中,我们使用波函数来描述系统的态,但当系统处于混合态时,单一的波函数描述不够完整。密度矩阵的引入提供了一种更一般的描述方式,能够同时包含纯态和混合态的信息。
密度矩阵它是一个厄米、正定的矩阵,通常用ρ表示。密度矩阵可以用来描述一个量子系统的状态,无论是处于纯态还是混合态。在纯态情况下,密度矩阵是一个投影矩阵,只有一个非零特征值为1,其余特征值为0。它可以表示系统处于一个确定的量子态,例如一个粒子的自旋向上。在混合态情况下,密度矩阵是一个非投影矩阵,即具有多个非零特征值的矩阵。它可以表示系统处于多个量子态的叠加状态,这些量子态具有一定的概率分布。
密度矩阵不仅包含了量子态的纯度信息,还包含了量子态之间的相干性和相关性信息。通过对密度矩阵的运算,可以计算出各种物理量的期望值,并进一步推导出系统的性质和行为。
3. 噪声中尺度量子NISQ
噪声中的尺度量子是指在量子计算中受到噪声和误差影响的系统。尺度量子通常用于描述量子比特或量子门操作的性能和可靠性。
在实际的量子计算中,量子系统容易受到环境干扰、量子比特之间的耦合、测量误差等各种噪声的影响。这些噪声会导致量子比特的退相干、非理想的量子门操作和测量结果的误差等问题,限制了量子计算的可靠性和精度。
尺度量子考虑的是在噪声影响下的量子计算的尺度和效能。它通常涉及以下几个方面:
- 量子比特保真度(Fidelity):量子比特的保真度是指量子比特实际状态与理想状态之间的相似度。在噪声中,保真度衡量了量子比特的退相干程度和受到噪声的影响程度。
- 量子门操作的保真度:量子门操作是对量子比特进行操作和演化的基本操作。在噪声中,量子门操作的保真度衡量了实际操作与理想操作之间的相似度,即量子门的准确性和精度。
- 量子纠错:量子纠错是一种技术手段,用于通过特定的算法和编码来纠正量子比特受到的噪声和误差。尺度量子研究中的一项重要任务是设计和优化有效的量子纠错方案,提高量子计算的可靠性和容错性。
3.1 退相干
退想干:量子比特的量子态由一个纯态演化为一个混合态。当量子比特处于纯态时,其量子态可以表示为一个复数的幅度和相位的组合。而当量子比特退相干时,其量子态变为一个混合态,其表示为一组概率分布,其中每个分布对应一个纯态的贡献。这意味着在退相干状态下,量子比特的量子信息和量子叠加态的特性会减弱,而经典概率的影响会增加。
4 量子原生
量子原生是指直接在量子计算机上执行的原始量子操作和量子门操作,而不是将问题转化为经典计算机上的量子模拟或优化算法。量子原生计算强调在量子硬件上使用原生的量子门操作和量子测量,以利用量子计算机的优势来解决特定的问题。
在量子原生计算中,问题的表述和算法设计与量子系统的物理特性密切相关。它可以涉及通过量子逻辑门和量子测量来构建量子电路,使用量子比特的叠加态和纠缠态进行计算,以及利用量子优势来解决特定的问题,如优化、模拟、机器学习等。
量子原生计算的主要优势是它允许直接利用量子计算机的潜力,通过充分利用量子比特之间的量子相互作用和量子叠加的性质,来执行计算和解决问题。这种方法可以在一些特定的应用领域中提供潜在的加速和优势,例如量子化学模拟、优化问题、机器学习等。
然而,量子原生计算也面临着一些挑战,包括量子比特的退相干、量子错误率、噪声和干扰等。解决这些挑战需要设计和优化量子原生算法,开发噪声抑制技术,并利用量子纠错等方法来提高计算的可靠性和稳定性。
5 什么是量子化?
日常生活中,描述一个物体的状态参数基本上都是连续的,比如说爬楼梯时,位于第几层,我们用海拔参数测量,可以测量得出3.3米。因为这些参数可以被分割成更小的部分,3.3米之后还能分的更细,如3.33米、3.333米等等。然而无限分割下去,直到不得不靠几个原子,这种单位去描述物体的长度时,量子效应就出场了。薛定谔方程告诉人们,一定会遇到不可分割的最小单位,这种最小单位统称为量子。这种现象被称为量子化。
量子化是指将经典物理系统或现象转化为符合量子力学规则的描述和处理方式的过程。在经典物理中,我们使用连续的数值来描述物理量,例如位置、速度或能量等。然而,在量子力学中,物理量是以离散的方式存在的,它们的取值被量子化为一系列离散的可能结果。
一个常见的例子是电子的能级。在经典物理中,电子的能量可以是任意值,但在量子物理中,电子的能量是量子化的,只能取特定的离散值,称为能级。当电子从一个能级跃迁到另一个能级时,它的能量变化是不连续的,而是以量子的形式进行跃迁(原子的光谱只会有几个峰值,而不是连续的谱线,这代表了原子内电子的能量,只会出现几种情况,电子不可能具有几种情况之外的中间值,这就叫能量的量子化。)。
6 什么是量子态?什么是态矢?
6.1 量子态的概念
量子态是描述量子系统的状态的概念。在量子力学中,一个物理系统可以处于多个可能的状态之一,而量子态就是描述这个系统所处状态的数学对象。量子态可以同时具有多个可能的状态,而不仅仅是单一的0或1。
量子态通常用波函数来表示。波函数是一个复数函数,它包含了关于量子系统在不同状态下的概率幅。波函数的平方模的平均值给出了观测到系统处于某个状态的概率。
-
概率幅:用于描述量子系统状态,是一个复数,它与态矢(或波函数)相关联。量子态可以同时具有多个可能的状态,而不仅仅是单一的0或1。概率幅是这些不同状态的复数振幅,用于描述量子比特处于每个可能状态的可能性。当量子比特处于叠加态时,它的量子态可以表示为不同状态的概率幅的叠加。例如,对于一个单量子比特,它可以处于状态和的叠加态,表示为,其中是复数概率幅。这意味着量子比特同时具有成为和两个状态的可能性。
-
相位:是概率幅的复数部分的角度,它描述了量子态的相对相位差。相位的变化可以影响概率幅的描写,但不会改变测量结果的概率分布。相位差是相对于一个参考相位而言的,通常我们选择参考相位为零。
量子态具有叠加的性质,这意味着系统可以处于多个可能的状态的叠加态。叠加态表示了系统同时具有多个状态的概率分布,直到我们对其进行测量,才能得到一个具体的结果。
通俗来说电子处于不同的能级就说明它处在不同的量子态,这样就可以区分出来不同的量子态。
态矢(State vector),也被称为量子态矢量或量子态,是用于描述量子系统状态的数学对象。在量子力学中,态矢是表示一个物理系统可能的状态的向量。
态矢通常用符号 ∣ ψ ⟩ |ψ⟩ ∣ψ⟩表示,其中 ψ ψ ψ是一个数学符号,表示量子系统所处的状态。概率幅表示为 ⟨ ψ ′ ∣ ψ ⟩ ⟨ψ'|ψ⟩ ⟨ψ′∣ψ⟩,其中 ∣ ψ ′ ⟩ |ψ'⟩ ∣ψ′⟩表示另一个可能的量子态。这个概率幅的模长的平方,即 ∣ ⟨ ψ ′ ∣ ψ ⟩ ∣ 2 |⟨ψ'|ψ⟩|^2 ∣⟨ψ′∣ψ⟩∣2,给出了测量时系统从态 ∣ ψ ⟩ |ψ⟩ ∣ψ⟩转变到态 ∣ ψ ′ ⟩ |ψ'⟩ ∣ψ′⟩的概率。
6.2 量子态的具体介绍
在量子理论中,描述量子态的向量称为态矢,态矢分为左矢和右矢。
右矢(ket):
∣ ψ ⟩ = [ c 1 , c 2 , . . . , c n ] T |ψ⟩=[c_1,c_2,...,c_n]^T ∣ψ⟩=[c1,c2,...,cn]T
左矢(bra):
⟨ ψ ∣ = [ c 1 ∗ , c 2 ∗ , . . . , c n ∗ ] ⟨ψ|=[c_1^*,c_2^*,...,c_n^*] ⟨ψ∣=[c1∗,c2∗,...,cn∗]
采用竖线和尖括号的组合描述一个量子态,其中每一个分量都是复数,右上角标T表示转置。这种形式表示量子态是一个矢量。右矢表示一个n×1的列矢量,左矢表示一个1×n的行矢量。另外,在讨论同一个问题时,如果左矢和右矢在括号内的描述相同的话,那么这两个矢量互为转置共轭。
两个态矢的内积和外积操作如下:
给定任意的两个量子态的矩阵(坐标)表示如下:
∣ α ⟩ = [ a 1 , a 2 , . . . , a n ] T |α⟩=[a_1,a_2,...,a_n]^T ∣α⟩=[a1,a2,...,an]T
∣ β ⟩ = [ b 1 , b 2 , . . . , b n ] T |β⟩=[b_1,b_2,...,b_n]^T ∣β⟩=[b1,b2,...,bn]T
内积:
⟨ α ∣ β ⟩ = ∑ i = 1 n a i ∗ b i ∗ ⟨α|β⟩=∑_{i=1}^na_i^* b_i^* ⟨α∣β⟩=i=1∑nai∗bi∗
量子力学中用波函数来描述一个量子态,而内积则是用来计算两个波函数之间的相似度的。内积的结果是一个复数,它描述了两个波函数之间的相似度。如果内积的结果为0,则说明两个波函数是正交的,即它们在空间中没有重叠部分。
外积:
∣ α ⟩ ⟨ β ∣ = [ a i b j ∗ ] n ∗ n = ∣ α ⟩ ⊗ ⟨ β ∣ |α⟩⟨β|={[a_ib_j^*]}_{n*n}=|α⟩\otimes⟨β| ∣α⟩⟨β∣=[aibj∗]n∗n=∣α⟩⊗⟨β∣
其中*表示复共轭。
6.3 克罗内克积
A是 m ∗ n m*n m∗n的矩阵,B是 p ∗ q p*q p∗q的矩阵
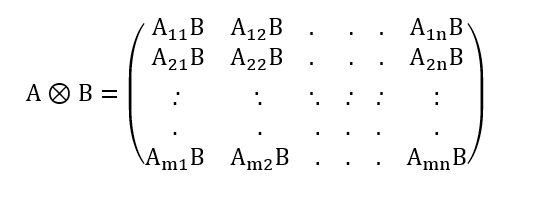
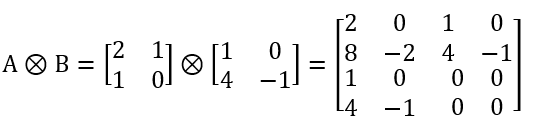
关于个人
An AI algorithm engineer. & open-source enthusiast.
- 🌱 Currently working in Hefei, China.
- 💬 If you have any questions about my blog, code, or project, please contact my email:
Jakesun2020@163.comor3895925098qq.com - ⭐ Welcome to WeChat official account: 自然语言处理CS
- ⭐ Welcome to blog: 自然语言处理CS
- ⭐ Welcome to Zhihu: 自然语言处理CS
- ⭐ Welcome to QQ group:自然语言处理CS or search for QQ group number: 909675022
🛠 研究方向 | Research Direction
- 💻 Artificial intelligence
- 🌐 Quantum computing
- 🛢 Machine learning
- 🔧 Deep learning
相关文章:
量子计算基础知识—Part1
1.什么是量子计算机? 量子计算机是基于量子力学原理构建的机器,采用了一种新的方法来处理信息,从而使其具有超强的功能。量子计算机使用Qubits处理信息。 2. 什么是量子系统? 一个量子系统指的是由量子力学规则描述和控制的物理…...

【PostgreSQL】【存储管理】表和元组的组织方式
外存管理负责处理数据库与外存介质(PostgreSQL8.4.1版本中只支持磁盘的管理操作)的交互过程。在PostgreSQL中,外存管理由SMGR(主要代码在smgr.c中)提供了对外存的统一接口。SMGR负责统管各种介质管理器,会根据上层的请求选择一个具体的介质管理器进行操作…...

VSCode安装图文详解教程
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl 教程说明 本教程旨在详细介绍VSCode的安装过程及其注意事项。 下载VSCode 请在官方网站 https://code.visualstudio.com/ 下载https://code.visualstudio.com/至本地&…...
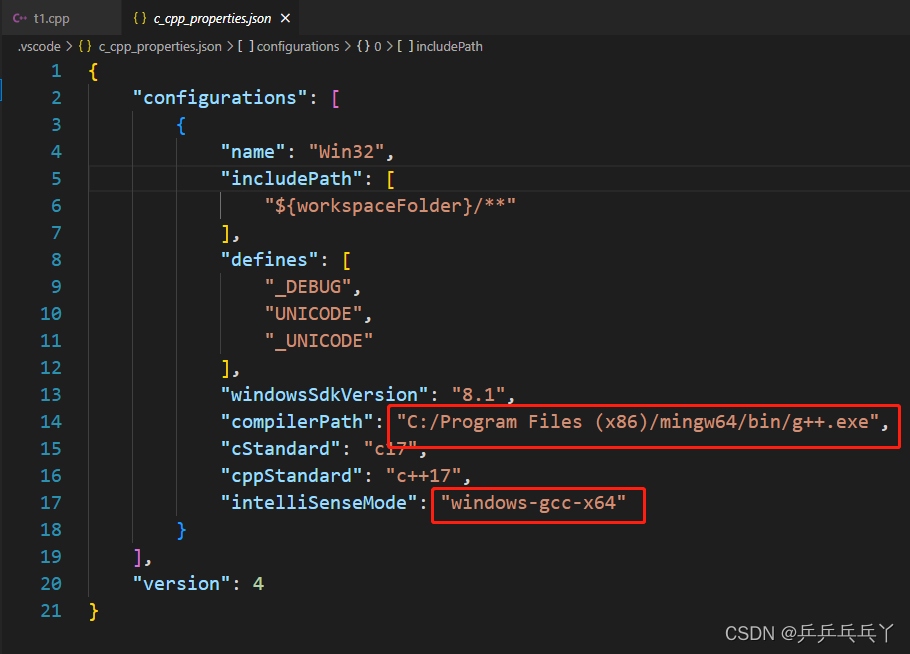
vscode 无法打开源文件
以下是c/c插件的intelligense设置情况: 解决办法: 重新安装vsode无用;重新下载mingw64,管用了!(我猜可能是之前换电脑移植文件的时候导致了部分文件丢失)...

1.8.C++项目:仿muduo库实现并发服务器之eventloop模块的设计
项目完整在: 文章目录 一、eventloop模块:进行事件监控,以及事件处理的模块二、提供的功能三、实现思想(一)功能(二)意义(三)功能设计 四、框架五、代码 一、eventloop模…...

Linux基本指令(二)
💓博主个人主页:不是笨小孩👀 ⏩专栏分类:数据结构与算法👀 C👀 刷题专栏👀 C语言👀 🚚代码仓库:笨小孩的代码库👀 ⏩社区:不是笨小孩👀 🌹欢迎大…...
)
量化交易全流程(五)
本节目录 策略回测 多因子模型 本节主要讨论回测相关的内容,包括两种不同的回测机制,即向量化回测和事件驱动回测;如何灵活使用开源工具来编写自己的回测程序;不同实现方式的优劣对比等。 在我们研究策略的时候,需要…...

聊聊MySQL的InnoDB引擎与MVCC
目录 一、InnoDB引擎 1.1逻辑存储结构 1). 表空间 2). 段 3). 区 4). 页 5). 行 1.2架构 1.2.1内存结构 1). Buffer Pool 2). Change Buffer 3). Adaptive Hash Index 4). Log Buffer 1.2.2磁盘结构 1). System Tablespace 2). File-Per-Table Tablespaces 3). …...
小病变检测:Gravity Network for end-to-end small lesion detection
论文作者:Ciro Russo,Alessandro Bria,Claudio Marrocco 作者单位:University of Cassino and L.M. 论文链接:http://arxiv.org/abs/2309.12876v1 内容简介: 1)方向:医学影像中小病变检测 2࿰…...

Flink--7、窗口(窗口的概念、分类、API、分配器、窗口函数)、触发器、移除器
星光下的赶路人star的个人主页 内心的平静始于不再让他人掌控你的感情 文章目录 0、前言1、窗口(Window)1.1 窗口的概念1.2 窗口的分类1.3 窗口API概览1.4 窗口分配器(Window Assigner)1.4.1 时间窗口1.4.2 计数窗口 1.5 窗口函数…...
vscode 注释插件koroFileHeader
https://blog.51cto.com/u_15785499/5664323 https://blog.csdn.net/weixin_67697081/article/details/129004675...
Centos7安装php-fpm
目录 第一步:查看系统IP地址和网卡名称 第二步:更改网络配置模式 第三步、重启network 查看iptablies ,将第十行,十一行删除 第四步:关闭config 第五步:创建nginx 文件夹 查看目录下的文件 进入nginx文件夹 第…...

计算机网络(五):运输层
参考引用 计算机网络微课堂-湖科大教书匠计算机网络(第7版)-谢希仁 1. 运输层概述 之前所介绍的计算机网络体系结构中的物理层、数据链路层以及网络层它们共同解决了将主机通过异构网络互联起来所面临的问题,实现了主机到主机的通信ÿ…...

适合在校学生的云服务器有哪些?
随着云计算技术的发展,越来越多的学生开始使用云服务器来进行学习和实践。对于学生来说,选择一款便宜的云服务器不仅可以帮助他们降低成本,还可以提高学习和实践的效率。本文将介绍几款适合学生使用的便宜云服务器。 1、腾讯云学生服务器【点…...
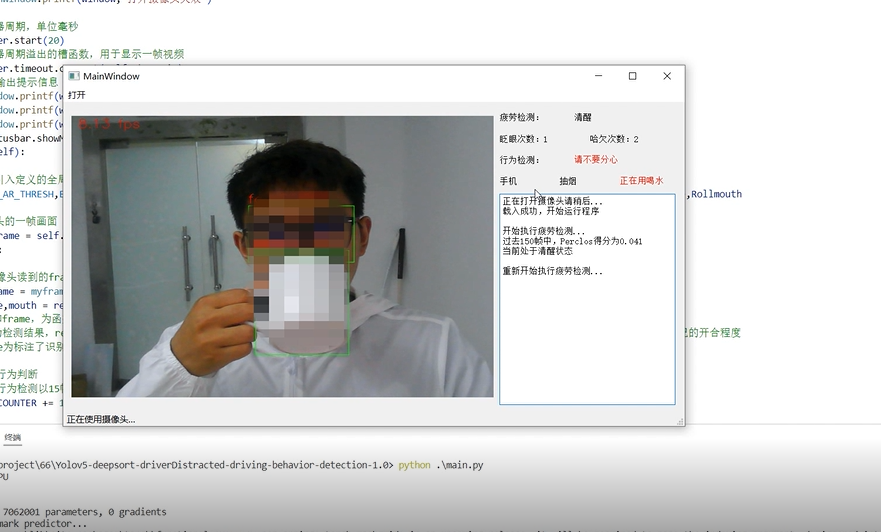
计算机竞赛 深度学习驾驶行为状态检测系统(疲劳 抽烟 喝水 玩手机) - opencv python
文章目录 1 前言1 课题背景2 相关技术2.1 Dlib人脸识别库2.2 疲劳检测算法2.3 YOLOV5算法 3 效果展示3.1 眨眼3.2 打哈欠3.3 使用手机检测3.4 抽烟检测3.5 喝水检测 4 最后 1 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 基于深度学习的驾…...
想要精通算法和SQL的成长之路 - 验证二叉搜索树和不同的二叉搜索树
想要精通算法和SQL的成长之路 - 验证二叉搜索树和不同的二叉搜索树 前言一. 验证二叉搜索树二. 不同的二叉搜索树三. 不同的二叉搜索树II 前言 想要精通算法和SQL的成长之路 - 系列导航 二叉搜索树的定义: 节点的左子树只包含 小于 当前节点的数。节点的右子树只包…...
SpringCloudAlibaba 相关组件的学习一
目录 前言 系统架构演变 1、单体架构 2、垂直架构 3、分布式架构 4、SOA架构 5、微服务架构 一、微服务架构的介绍 1、微服务架构的常见问题 2 微服务架构的常见概念 2.1 服务治理 2.2 服务调用 2.3 服务网关 2.4 服务容错 2.5 链路追踪 3、微服务架构的常用解决…...

【C语言 模拟实现strncpy函数、strncat函数、strncmp函数、strstr函数】
C语言程序设计笔记---026 C语言之模拟实现strncpy函数、strncat函数、strncmp函数、strstr函数1、介绍strncpy函数1.1、模拟实现strncpy函数 2、介绍strncat函数2.1、模拟实现strncat函数 3、介绍strncmp函数3.1、模拟实现strncmp函数 4、介绍strstr函数4.1、模拟实现strstr函数…...

Mongodb7启动报错排除解决方案
一: 报错信息: [rootwww log]# journalctl -xe -- Unit mongodb.service has begun starting up. /usr/local/mongodb/mongdb7/bin/mongod --help for more information 10月 03 13:47:39 www.yhchange.com systemd[1]: mongodb.service: control process exited, …...

王杰国庆作业day5
...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
