01BFS最短距离的原理和C++实现
时间复杂度
O(n),n是边数。
使用前提
边的权只有两种:0,1。
典型场景
n个端点的无向图,编号范围[0,n)。Edges0表示{{n1,n2},...{n3,n4}}表示n1和n2,n3和n4之间有路联接。Edges1表示{{n1,n2},...{n3,n4}}表示n1和n2,n3和n4之间有损坏的路连接。要想让s和d之间至少有一条通道,最小需要维修多少条路。如果无法到达,请返回-1。可能有环,但无自环,重边,可能不联通。
解题思路
可以用类似上章的思路,没损害的路加到pre中,损坏的路加到que中。距离相等的点,谁先谁后无所谓。需要维修的路入队的时候不能计算最短距离,因为不一定是最短边。改在入队计算最短距离,第一层循环记录最短距离。
核心代码
class CBFS1
{
public:CBFS1(vector<vector<int>>& vNeiB0, vector<vector<int>>& vNeiB1, int s){m_vDis.assign(vNeiB0.size(), -1);//m_vDis[s] = 0;queue<int> pre;pre.emplace(s);for (int i = 0; pre.size(); i++){queue<int> dp;while (pre.size()){const int cur = pre.front();pre.pop();if (-1 != m_vDis[cur]){continue;}m_vDis[cur] = i;for (const auto next : vNeiB0[cur]){pre.emplace(next);}for (const auto next : vNeiB1[cur]){dp.emplace(next);}}dp.swap(pre);}}
public:vector<int> m_vDis;
};测试样例
#define CBFS CBFS1
class CDebugBFS : public CBFS
{
public:
using CBFS::CBFS;
void Assert(const vector<int>& vDis)
{
for (int i = 0; i < vDis.size(); i++)
{
assert(vDis[i] == m_vDis[i]);
}
}
};
struct CDebugParam
{
int n;
vector<vector<int>> edges0;
vector<vector<int>> edges1;
int s;
vector<int> dis;//答案
};
int main()
{
vector<CDebugParam> params = { {1,{},{},0,{0}},{2,{},{},0,{0,-1}},{2,{{0,1}},{},0,{0,0}},{2,{},{{0,1}},0,{0,1}},
{6,{}, { {0,1},{1,2},{1,3},{2,4},{4,5},{3,5}},0,{0,1,2,2,3,3} },
{6,{{3,5}}, { {0,1},{1,2},{1,3},{2,4},{4,5}},0,{0,1,2,2,3,2} }
};
for (const auto& par : params)
{
auto vNeiB0 = EdgeToNeiBo(par.n, par.edges0);
auto vNeiB1 = EdgeToNeiBo(par.n, par.edges1);
CDebugBFS bfs(vNeiB0, vNeiB1,par.s);
bfs.Assert(par.dis);
}
}
类似场景
魔塔经典问题,砸墙需要一个锄头,没墙的地方可以随便移动,如果用尽可能少的锄头到达目的地。许多游戏经过箭塔附件时,会遭到箭塔攻击。如何已最小的损坏通过箭塔。
用双向队列优化
| 当前状态 | 操作 | 新状态 |
| 空 | 处理结束 | |
| 首尾入队 | 一种最短距离 | |
| 一种最短距离 | 出队 | 状态不变或变为空 |
| 队首入队 | 一种最短距离或两种最短距离 | |
| 队尾入队 | 一种最短距离或两种最短距离 | |
| 二种最短距离 | 出队 | 状态不变或变为一种最短距离 |
| 队首入队 | 两种最短距 | |
| 队尾入队 | 两种最短距 | |
class C01BFSDis
{
public:C01BFSDis(vector<vector<int>>& vNeiB0, vector<vector<int>>& vNeiB1, int s){m_vDis.assign(vNeiB0.size(), -1);std::deque<std::pair<int,int>> que;que.emplace_back(s,0);while (que.size()){auto it = que.front();const int cur = it.first;const int dis = it.second;que.pop_front();if (-1 != m_vDis[cur]){continue;}m_vDis[cur] = it.second;for (const auto next : vNeiB0[cur]){if (-1 != m_vDis[next]){continue;} que.emplace_front(next,dis);}for (const auto next : vNeiB1[cur]){if (-1 != m_vDis[next]){continue;}que.emplace_back(next, dis+1);}}}
public:vector<int> m_vDis;
};测试环境
Win10 VS2022 C++17
下载
doc文档下载(排版好):
https://download.csdn.net/download/he_zhidan/88348653
源码下载:
https://download.csdn.net/download/he_zhidan/88383828
相关文章:

01BFS最短距离的原理和C++实现
时间复杂度 O(n),n是边数。 使用前提 边的权只有两种:0,1。 典型场景 n个端点的无向图,编号范围[0,n)。Edges0表示{{n1,n2},...{n3,n4}}表示n1和n2,n3和n4之间有路联接。Edges1表示{{n1,n2},...{n3,n4}}表示n1和n2,n3和n4之间…...
)
【洛谷 P5266】【深基17.例6】学籍管理 题解(映射+分支)
【深基17.例6】学籍管理 题目描述 您要设计一个学籍管理系统,最开始学籍数据是空的,然后该系统能够支持下面的操作(不超过 1 0 5 10^5 105 条): 插入与修改,格式1 NAME SCORE:在系统中插入姓…...
10.03
代码 #include <iostream>using namespace std; class cz { private:int num1; //实部int num2; //虚部 public:cz(){}cz(int a,int b):num1(a),num2(b){}cz(const cz &other):num1(other.num1),num2(other.num2){}~cz(){}const cz operator(const cz &othe…...

链表单向链表跳跃链表
单向链表 link list t数组的局限:编译期就需要知道大小; 内存连续,插入困难 // 链表节点类 包含一个信息 和指向下一个 节点的指针clas IntLLNode{public:IntLLNode(){// 默认构造函数 没有info信息nextPtr_ 0;// 空指针}IntLLNode(int …...
博客无限滚动加载(html、css、js)实现
介绍 这是一个简单实现了类似博客瀑布流加载功能的页面,使用html、css、js实现。简单易懂,值得学习借鉴。👍 演示地址:https://i_dog.gitee.io/easy-web-projects/infinite_scroll_blog/index.html 代码 index.html <!DOCT…...
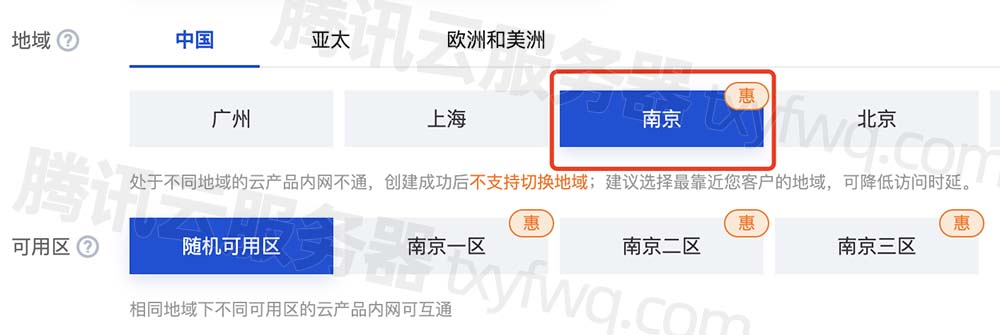
腾讯云南京服务器性能如何?南京服务器测速IP地址
腾讯云服务器南京地域怎么样?南京地域很不错,正好处于中间的位置,南方北方用户均可以选择,网络延迟更低速度更快,并且目前南京地域有活动,南京地域可用区可选南京一区、南京二区和南京三区,腾讯…...

MySQL和Oracle中,语法的不同点以及如何在xml中书写日期比较大小
众所周知mysql和oracle的语法有点相识,又有点不同。 在MySQL和Oracle中,语法的不同点有以下几个方面: 数据类型:MySQL和Oracle支持的数据类型有所不同,比如MySQL支持的数据类型包括:整型、浮点型、字符型、…...
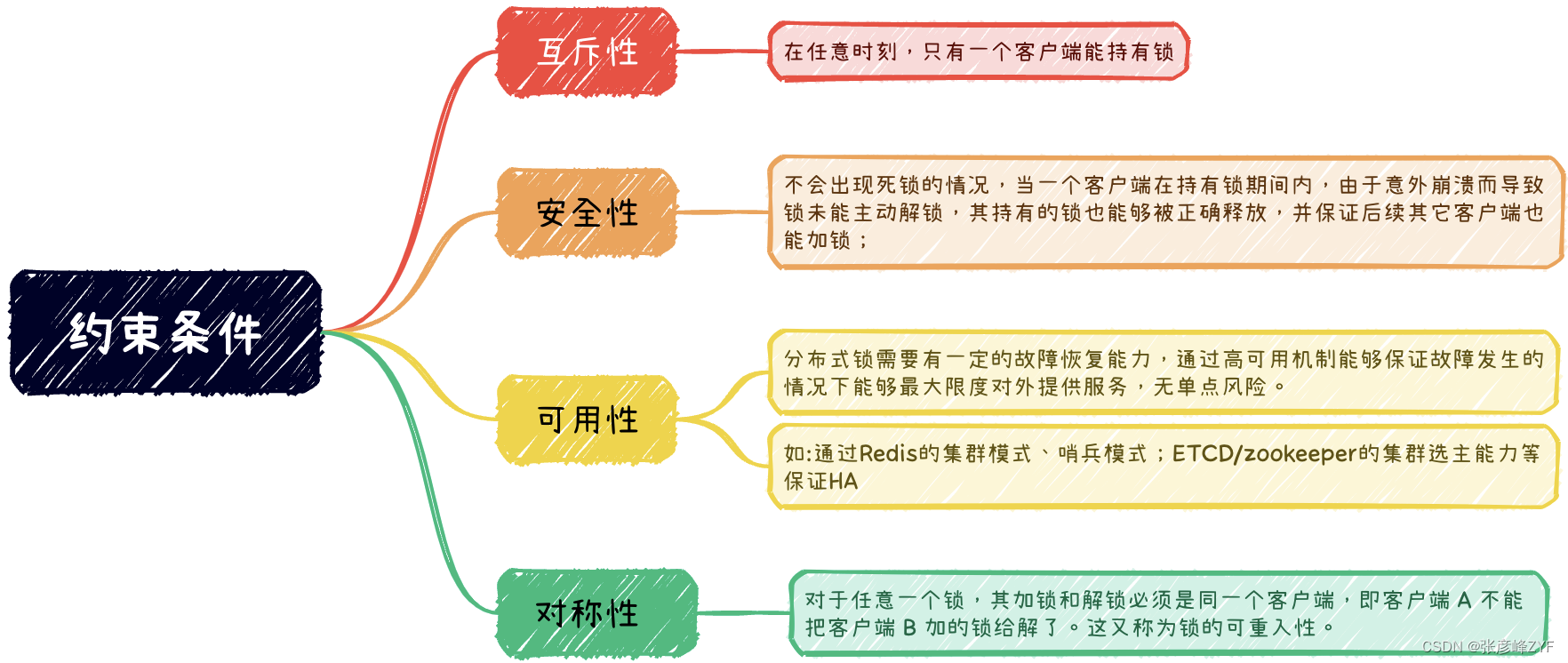
谈谈Redis分布式锁
目录 一、回顾分布式锁 (一)理解分布式锁的定义 (二)分布式锁的约束条件 (三)分布式锁常见实现方式 基于数据库的分布式锁 基于缓存的分布式锁 基于分布式一致性算法的分布式锁 基于文件系统的分布…...
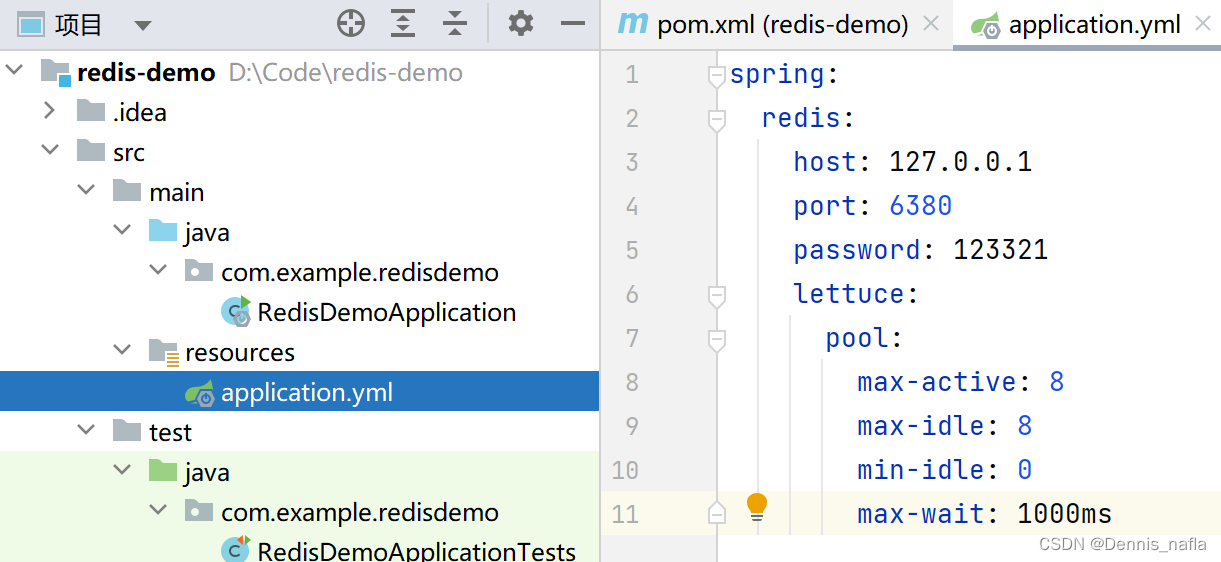
Redis的java客户端-RedisTemplate光速入门
一.创建springboot项目 二.引入2个依赖 <!-- redis依赖-->这个已经引入了,因为创建的时候勾选了<dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId><…...
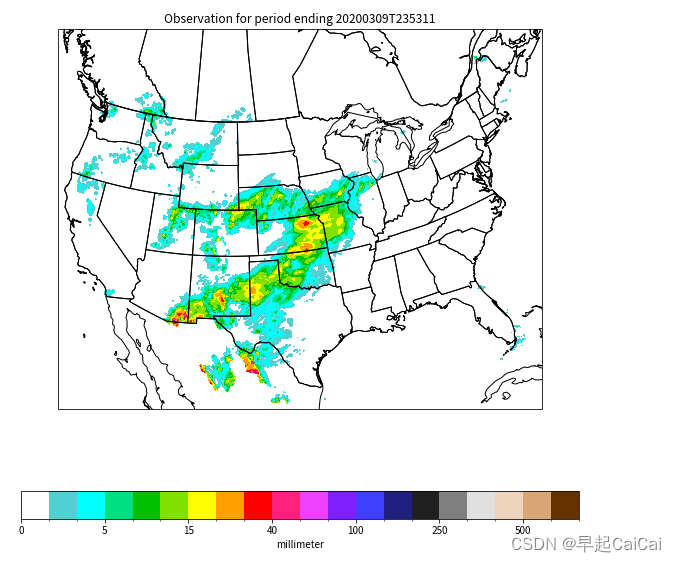
格点数据可视化(美国站点的日降雨数据)
获取美国站点的日降雨量的格点数据,并且可视化 导入模块 from datetime import datetime, timedelta from urllib.request import urlopenimport cartopy.crs as ccrs import cartopy.feature as cfeature import matplotlib.colors as mcolors import matplotli…...

YoloV8改进策略:LSKNet加入到YoloV8中,打造更适合小目标的YoloV8
文章目录 摘要论文:LSKNet:大选择核网络在遥感目标检测中的应用1、简介2、相关工作2.1、遥感目标检测框架2.2、大核网络2.3、注意力/选择机制3、方法3.1、LSKNet架构3.2、大核卷积3.3、空间核选择4、实验4.1、数据集4.2、实现细节4.3、消融实验4.4、主要结果4.5、分析5、结论…...

力扣-303.区域和检索-数组不可变
Idea 需计算数组nums在下标right 和 left-1 的前缀和,然后计算两个前缀和的差即可。 需要注意的是,当left为0的时候,如果还是left-1则会发生数组访问越界错误。 AC Code class NumArray { public:vector<int> sum;NumArray(vector<…...

web:[极客大挑战 2019]LoveSQL
题目 打开页面显示如下 查看源代码,查到一个check.php,还是get传参 尝试账号密码输入 题目名为sql,用万能密码 1or 11# 或 admin or 11 给了一段乱码,也不是flag 查看字段数 /check.php?usernameadmin order by 3%23&pass…...

数据结构—快速排序(续)
引言:在上一篇中我们详细介绍了快速排序和改进,并给出了其中的一种实现方式-挖坑法 但其实快速排序有多种实现方式,这篇文章再来介绍其中的另外两种-左右指针法和前后指针法。有了上一篇挖坑法的启示,下面的两种实现会容易许多。 …...
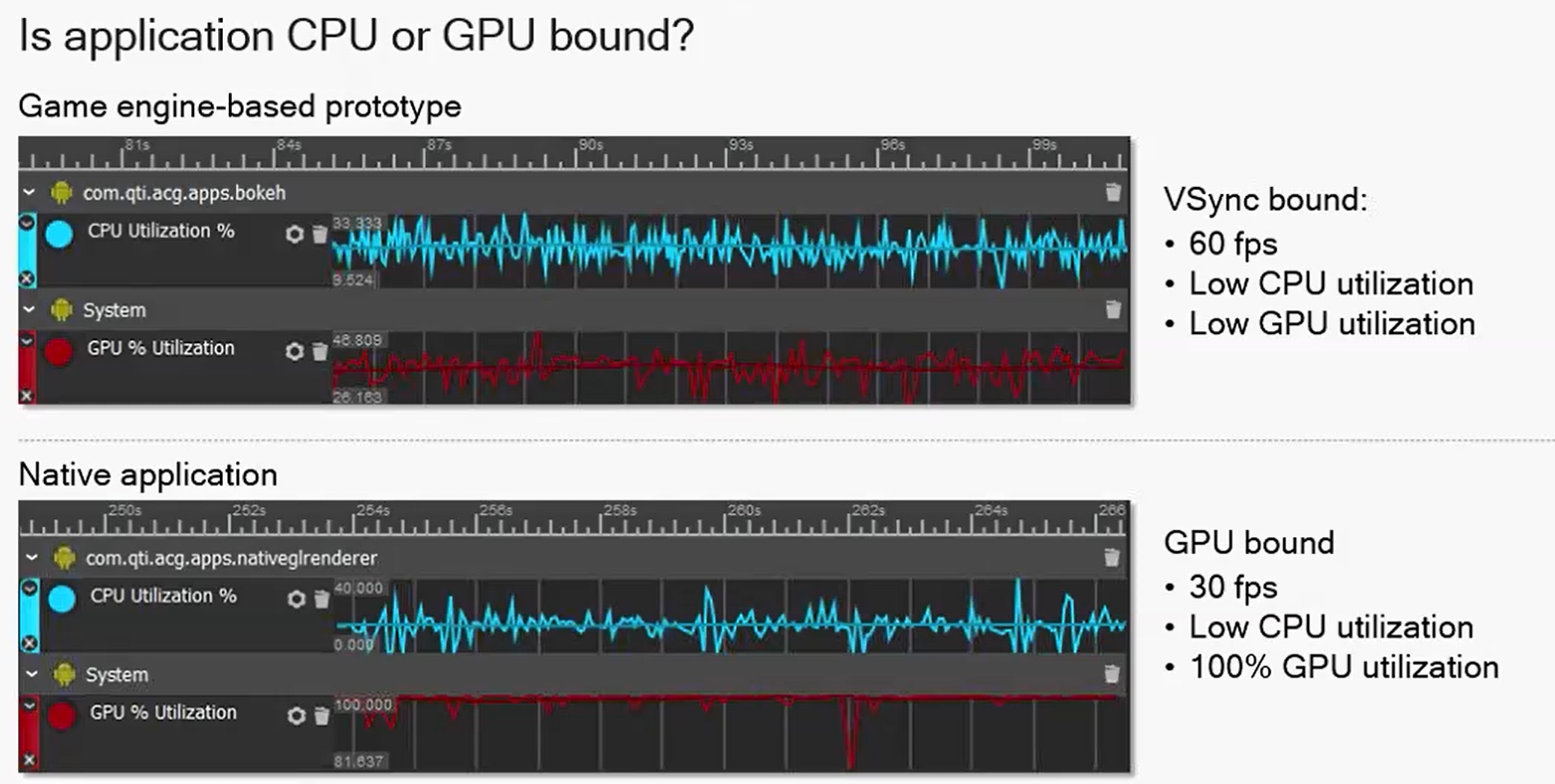
Snapdragon Profiler分析Android GPU
Snapdragon Profiler(骁龙分析器)是一款性能分析软件,在Windows、 Mac、和 Linux平台上都可以运行,主要是用来分析使用了高通骁龙处理器的Android设备。 Snapdragon Profiler通过USB连接这些Android设备,开发者可以用…...
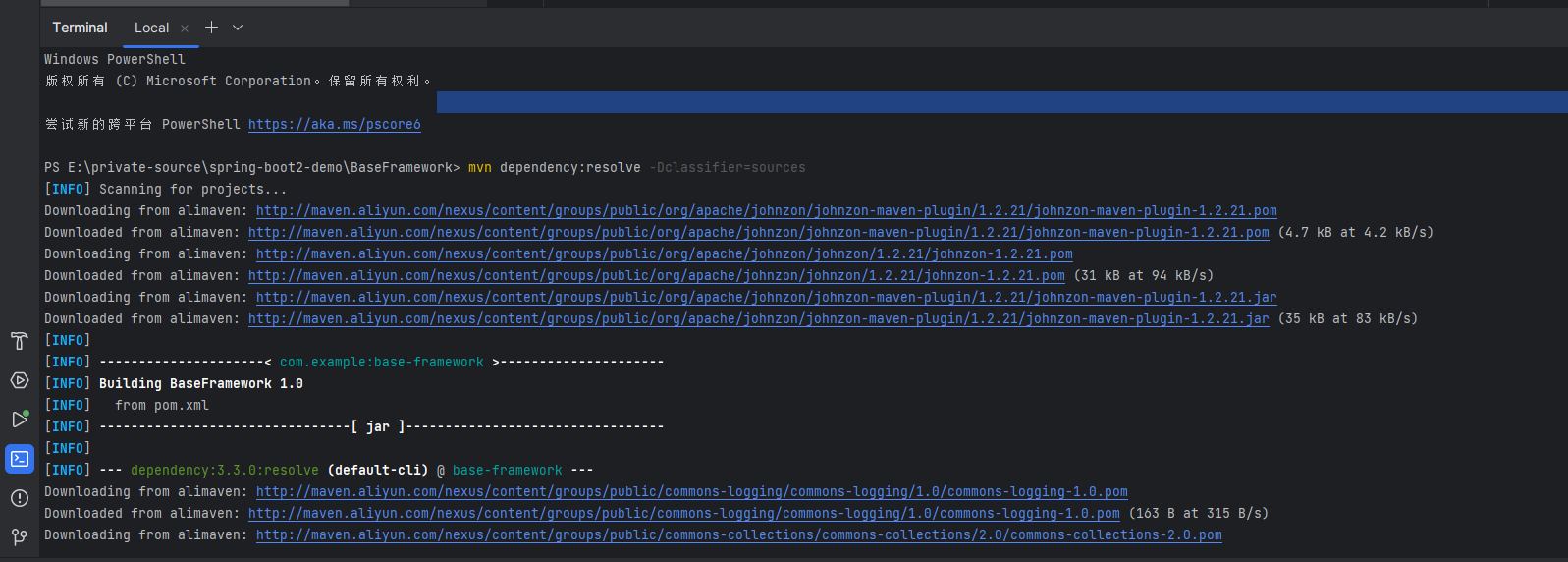
Cannot download sources:IDEA源码无法下载
问题 Swagger的相关包,无法看到注释; 在class文件的页面,点击下载源码,源码下载不了,IDEA报下面的错误。 报错 Cannot download sources Sources not found for: io.swagger.core.v3:swagger-annotations:2.2.9 解决…...
)
从零开始学习 Java:简单易懂的入门指南之IO字符流(三十一)
IO流之字符流 1. 字符流1.1 字符输入流【Reader】1.2 FileReader类构造方法读取字符数据 1.3 字符输出流【Writer】1.4 FileWriter类构造方法基本写出数据关闭和刷新写出其他数据 2. IO异常的处理JDK7前处理JDK7的处理JDK9的改进 3. 综合练习练习1:拷贝文件夹练习2&…...
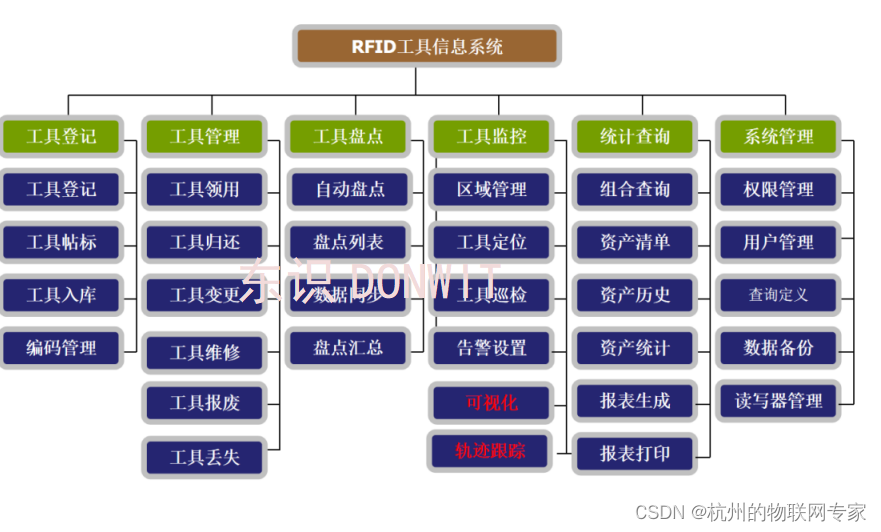
监狱工具管理系统-监狱劳动工具管理系统
监狱劳动工具管理系统(智工具DW-S308)是依托互3D技术、云计算、大数据、RFID技术、数据库技术、AI、视频分析技术对工具进行统一管理、分析的信息化、智能化、规范化的系统。 当前各级监狱工器具管理更多的是借助于传统的人工管理方法和手段,数据的采集和录入一直以…...

蓄水池算法
题目: 假设有一组数据流元素有 N 个(事先不知道 N 具体值),我们希望选择 n 个样本(N > n),使用怎样的策略进行抽样可以使得数据流中每个元素被选择的概率恰为 n / N 结论: 创建大…...

作业 day4
完成父子进程通信...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...
