2024级199管理类联考之数学基础(上篇)
管理类考试介绍
- 管理综合200分,时间3小时
- 数学:75分/25题,是拉开差距的核心模块
- 问题求解题:15个,5选一
- 条件充分性判断:10个,结合两个条件选择答案
- 条件一充分,条件二不充分:A
- 条件一不充分,条件二充分:B
- 条件一充分,条件二充分:D
- 条件一不充分,条件二不充分,联合充分:C
- 条件一不充分,条件二不充分,联合不充分:E
- 逻辑:60分/30题,形式、论证、分析推理【大部分40-50分】
- 写作:65分/2篇作文,论证有效性分析600字,论说文700字【大部分35-45分】
- 数学:75分/25题,是拉开差距的核心模块
- 英语二 100分,3小时
数学概述
算术(平均1-2题)
有理数和无理数
实数分为有理数和无理数,两者区别在于能否写成两个整数之比
- 有理数包括整数和分数
- 整数:正整数、0、负整数
- 自然数:0和正整数统称为自然数,即非负整数
- 无理数:无限不循环小数,如e、log等
- 经常考察一个式子同时含有有理数与无理数部分,整体等于0
- 解题思路: 有理数部分合并,无理数部分合并,分别为0
质数与合数
- 质数/素数:大于1的整数,除了1和自身之外不能被其他正整数整除的数(即约数只有1和质数本身)
- 合数:大于1的整数,除了1和自身之外还能被其他正整数整除的数(即约数包括1、本身以及其他约数)
- 注意
- 1既不是质数也不是合数,2是唯一的偶质数;质因数表示既是一个数的约数又是质数的数
- 20以内8大质数:2,3,5,7,11,13,17,19
奇数偶数
- 奇数:不能被2整除的整数,表示为2k+1
- 偶数:能被2整除的整数,包括0,表示为2k
整除/约数/倍数
- 常见数整除的特征
- 能被2整除的数:个位数字为0、2、4、6、8
- 能被3整除的数:各位数字之和必能被3整除
- 能被4整除的数:末两位数字必能被4整除
- 能被5整除的数:个位数字为0或5
- 能被6整除的数:同时满足能被2和3整除
- 能被8整除的数:末三位数字必能被8整除
- 能被9整除的数:各位数字之和能被9整除
- 能被10整除的数:个位数字为0
- 公约数:几个自然数公有的约数,称为这几个自然数的公约数,公约数中最大的公约数称为这几个自然数的最大公约数
- 最小公倍数:几个自然数公有的倍数(排除0以外)

绝对值非负性
- 正数的绝对值是它本身,负数是它的相反数,零的绝对值还是0
- 几何意义:表示一个实数a在数轴上所对应的点到原点0的距离值,如|x-b| =a表示与b点的距离为a
- 非负符号:绝对值、偶次乘方、开偶次根号
- 常见考试场景:含有绝对值和开偶次根号或者偶次乘方
- 解题思路:保持各项为0即可
绝对值两个模型
- 和模型(函数曲线为平底锅型):存在最小值
- |x-a|+|x-b|几何意义表示数轴上x到a与b点的距离之和,当x在a点与b点之间存在最小值,即最小距离值为|a-b|,x不在两者之间则趋于正无穷.
- 若f(x) = |x-a|+|x-b|+|x-c|,也无最大值,当x在a与c之间时且x=b时存在最小值|c-a|
- 即奇数个点取中间点有最小值,偶数个点取中间两个数之间点有最小值
- 差模型(函数曲线为Z字型):既有最小值也存在最大值
- |x-a|-|x-b|几何意义表示数轴上x到a与b点的距离之差,当x在a点与b点之外时存在最大值|a-b|和最小距离值为-|a-b|
三角不等式(求最值)
- |a + b| <= |a|+|b|;等号成立条件ab>=0;
- |a - b| <= |a|+|b|;等号成立条件ab<=0;
- 三角不等式主要考察取等号条件,消去参数是核心
比和比例
- 比例基本性质
- 比例的前项和后项同时乘或除以不含0的相同的数,比值不变
- a:b=c:d <==> b:a=d:c<=> a:c=b:d<=>c:a=d:b
- 比例定理
- 合比定理:a/b = c/d <=> (a+b)/b=(c+d)/d
- 分比定理:a/b = c/d <=> (a-b)/b=(c-d)/d
- 合分比定理:a/b = c/d <=> (a+b)/a-b=(c+d)/c-d
- 等比定理:a/b = c/d = e/f =a+c+e/b+d+f(b+d+f !=0)
- 解题思路
- 分数比化解为整数比
- 需要引入比例系数k,化抽象比例为具体数值计算求解

平均值定理(均值不等式)
- 算术平均数:x1+x2+...+xn/n
- 几何平均数:设n个正数x1...xn称x=n次根号下x1..xn
- 基本定理
- x1...xn为正数时,它们的算术平均值不小于几何平均值,即x1...xn/n>=n次根号下x1...xn,当且仅当x1=...=xn,等号成立
- 若a>0,b>0,则a+b/2>=根号下ab(a+b>=2根号下ab),当且仅当a=b时等号成立(一正二定三相等)
- 积为定值,则求和存在最小值
- 和为定值,则求积存在最大值
- a+1/a>=2(a>0)当且仅当a=1时取最小值2,即对正数而言互为倒数的两个数之和不小于2
- 扩展
- a+b+c>=3*3次根号下abc(a、b、c>0)当且仅当a=b=c时取得等号
- a+b+c+d>=4*4次根号下abcd(a、b、c、d>0)当且仅当a=b=c=d时取得等号

整式与分式(平均1-2题)
因式分解
- 概念:把一个多项式化成几个整式的积的形式,本质就是化和为积,例如x^2 + 3x +2 = (x+2)(x+1)
- 注意:因式分解必须在指定的范围内分解到不能再分解为止
- 常用方法
- 分组分解法:例如am+bm+an+bn=(a+b)(m+n)
- 平方差公式:a^2-b^2=(a-b)(a+b)
- 完全平方公式:(a+_b)^2=a^2+-2ab+b^2
- 立方和与立方差公式:a^3+-b^3=(a+-b)(a^2-+ab+b^2)
- 三项完全平方和公式:(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc
- 完全立方和公式:(a+b)^3=a^3+3a^2b+3ab^2+b^3
- 拓展公式:(a-b)^2+(b-c)^2+(a-c)^2=2[a^2+b^2+c^2-ab-ac-bc]
- 十字相乘法:如x^2+5x+6=(x+2)(x+3)
因式定理
- 出题模式
- 代数式能被某个式子整除
- 某个式子是代数式的因式
- 代数式含有某某因式
- 解题模式
- 令因式为零,求得x的值
- 因式为根,根带入原式,代数式为零



代数式化简
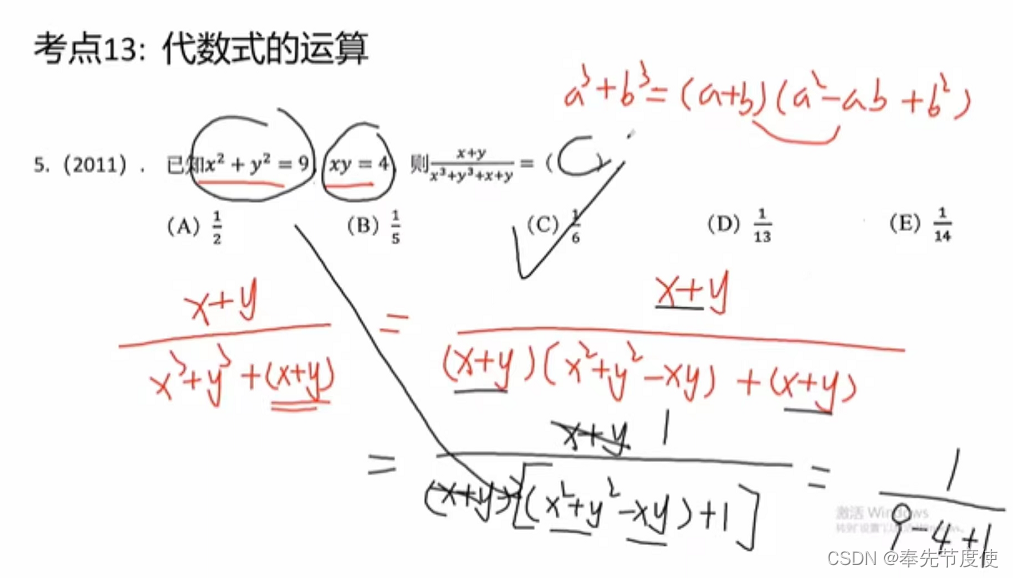

裂项相消法(数列求和或分式化简)
- 概念:实质就是因式分解的一种形式变换,以若干个分式相加,每个分式的分子都是1,然后重新组合,使之能消去一些项,最终达到求和目的
- 1/n(n+k)=1/k(1/n-1/(n+k)),即1/(大)(小)=1/大-小(1/小-1/大)

集合与函数(平均1-2题)
集合
- 性质
- 确定性:元素在一个集合或不在一个集合,不能模糊
- 相异性:集合中的元素不能重复
- 无序性:集合中的元素没有顺序要求
- 集合中运算包括并、交、补大部分使用文氏图表示

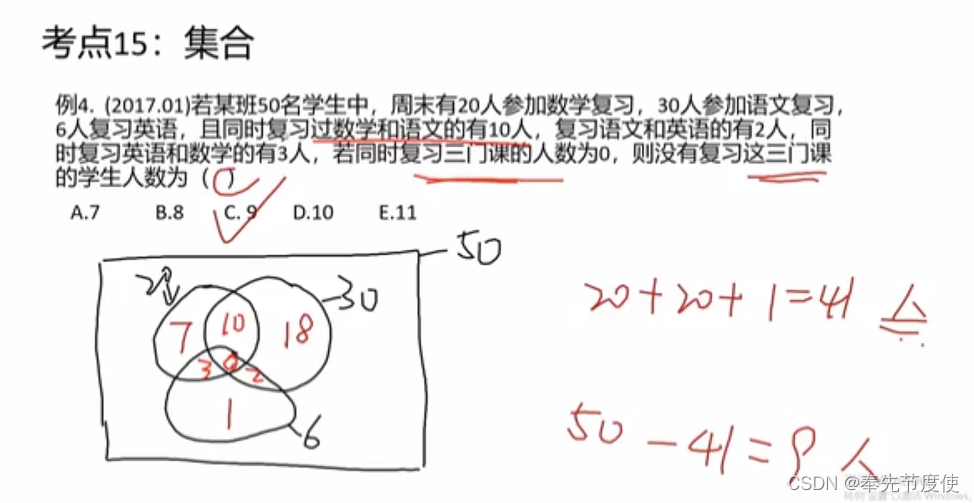
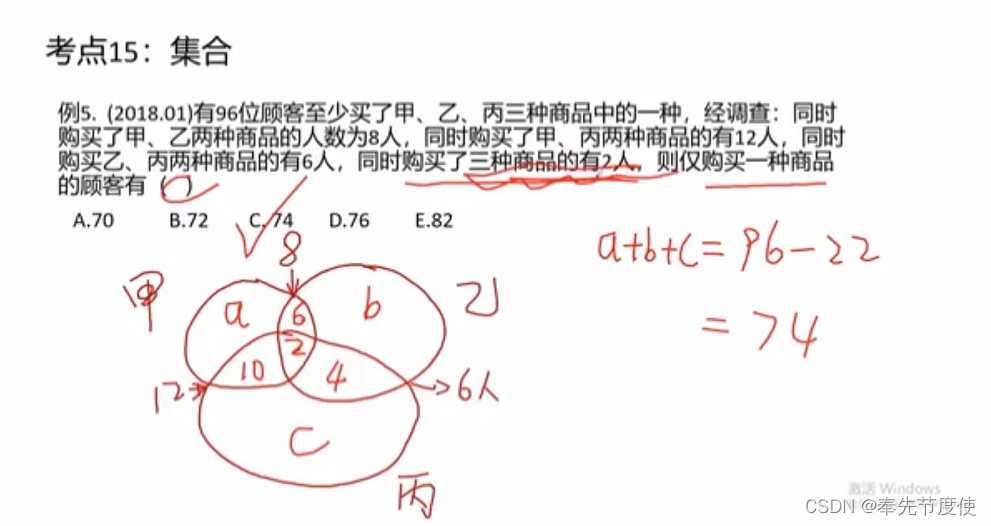
一元一次函数
- 定义:一般在某一变化过程中有两个变量x和y,如果给定一个x,相应确定一个y值,那么称y是x的函数,x是自变量,y是因变量
- 若两个变量x,y关系可以表示为y=kx+b(k、b为常数,k!=0),则称y是x的一次函数,当b=0时则y=kx(k!=0)称y是x的正比例函数。注意:一次函数都是一条直线

一元二次函数
- 基本定义
- y=ax^2+bx+c(a!=0,a、b、c是常数),对称轴x=-b/2a,顶点坐标(-b/2a,4ac-b^2/4a),最值在顶点处取得(a>0为最小值,a<0表示函数有最大值)
- 表达式
- 一般式:y=ax^2+bx+c
- 顶点式:y=a(x+b/2a)^2+4ac-b2/4a
- 两根式:y=a(x-x1)(x-x2)
- x1,x2表示函数与x轴交点的横坐标/函数的零点/对应一元二次方程的两个根
- 一元二次函数性质
- a决定抛物线的开口方向,a>0向上,a<0向下
- 对称轴-b/2a>0表示在y轴右侧,<0表示y轴左侧,=0表示对称轴就是y轴
- c>0表示抛物线与y轴的交点在原点上方,=0表示过原点,<0表示在原点下方
- 判别式吧b^2-4ac决定抛物线与x轴的交点个数,>0表示有两个,=0有一个且顶点在x轴上,<0表示无交点
- 若a+b+c=0,则抛物线过点(1,0);若a-b+c=0,则抛物线过点(-1,0)



指数函数与对数函数
- 指数函数
- 定义:y=a^x(a>0且a!=1)称为指数函数,x为自变量
- 运算法则
- a^m * a^n = a^m+n
- a^m / a^n = a^m-n
- (a^m)^n = a^mn
- (ab)^m = a^m*b^m
- a^0 = 1;a^-p = 1/a^p(a!=0)
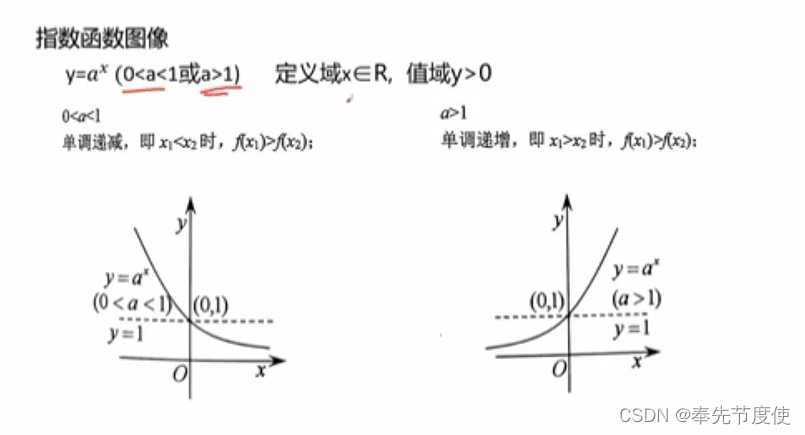

- 对数函数
- 定义:y=logaX(a>0且a!=1,x>0),a为底数,x为真数,y是以a为底x的对数
- 与指数互为反函数:a^m = b 《=》m=logab
- 运算法则
- logaMN=logaM+logaN
- logaM/N=logaM-logaN
- logaM^n=nlogaM
- loga^Nb^M=M/Nlogab
- 换底公式
- logaN=logbN/logba
- loga1=0;logaa=1;lg2+lg5=1;
- 定义:y=logaX(a>0且a!=1,x>0),a为底数,x为真数,y是以a为底x的对数


方程与不等式(平均2-4题)
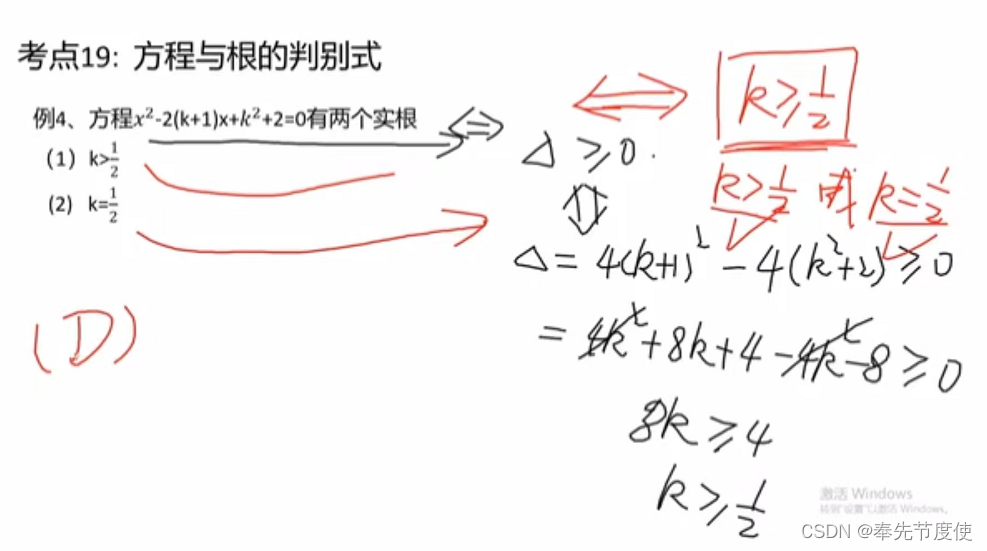
方程与根的判别式
- 一元一次方程:只含有一个未知数,并且未知数的最高次数为1,其中方程ax+b=0(x为未知数,a!=0)为标准一元一次方程形式,方程的解为x=-b/a;
- 一元二次方程:ax^2+bx+c=0(a!=0),a是二次项系数,b是一次项系数,c是常数项
- 根的判别式b^2-4ac
- >0时,方程有两个不等实根,根x=-b+-根号下b^2-4ac/2a
- =0时,存在两个相等实根,x=-b/2a
- <0时,方程无实根
- b^2-4ac联考中自然语言表达
- b^2-4ac=0
- 方程有两个相等实根/重实根
- 函数抛物线与x轴有且仅有一个交点/零点
- 抛物线与x轴相切
- 函数是一个完全平方公式
- 函数抛物线的最大/小值为0
- 仅存在一个x使得ax^2+bx+c=0成立
- b^2-4ac>0
- 方程有两个不相等的实数根
- 抛物线与x轴相交/有两个交点
- 函数或方程有两个零点
- 直线与抛物线有两个交点
- b^2-4ac<0
- 方程没有实数根
- 函数抛物线与x轴没有交点/零点
- 抛物线与x轴相离
- 直线与抛物线无交点
- 二次函数图像恒位于x轴上方/下方
- b^2-4ac>=0
- 方程有两个实数根
- 方程有两个正根
- 方程有两个负根
- 方程有根
- b^2-4ac=0
- 根的判别式b^2-4ac
- 是否对二次项系数a=0进行讨论
- 如果题目中明确二次函 数、一元二次方程、一元二次不等式、抛物线等则默认a!=0
- 若题目知识表示是函数、方程、不等式,则需要对a是否为0进行分类讨论
韦达定理
- 定义:ax^2+bx+c=0(a!=0)的两个根为x1,x2,则
- x1+x2=-b/a
- x1*x2=c/a
- 扩展公式
- x1^2+x2^2=(x1+x2)^2-2x1x2
- x1^3+x2^3=(x1+x2)[(x1+x2)^2-3x1x2]
- |x1-x2|=根号下b^2-4ac/|a|
- |x1-x2|不同自然语言表达形式
- 方程两根之差的绝对值
- 方程两根之间的距离
- 函数抛物线截得x轴的长度
- 函数抛物线与两坐标轴围成的三角形的底边长
- |x1-x2|不同自然语言表达形式

方程根的分布
- 根的分布是个综合问题,需要同时使用判别式和韦达定理
- 一元次方程ax^2+bx+c=0(a!=0)有两个正根
- b^2-4ac>=0
- x1+x2=-b/a>0
- x1x2=c/a>0
- 一元次方程ax^2+bx+c=0(a!=0)有两个负根
- b^2-4ac>=0
- x1+x2=-b/a<0
- x1x2=c/a>0
- 一元次方程ax^2+bx+c=0(a!=0)有一个负根,一个正根
- b^2-4ac>0
- x1x2=c/a<0
- 一元次方程ax^2+bx+c=0(a!=0)有两个根x1,x2且满足m<x1<n,p<x2<q

- f(m)f(n)<0
- f(p)f(q)<0
- 一元次方程ax^2+bx+c=0(a!=0)有两个根x1,x2且一根大于k,一根小于k
- 则无论a>0还是a<0都有af(k)<0
- 一元次方程ax^2+bx+c=0(a!=0)有两个正根
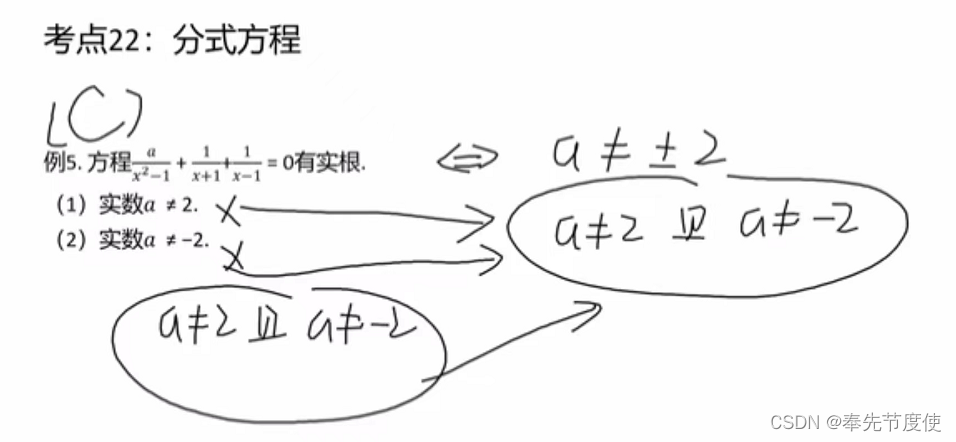
分式方程
- 思路就是将分式方程转换成整式方程
- 特殊解法:换元法(整体思维),还需要考虑是否存在增根等
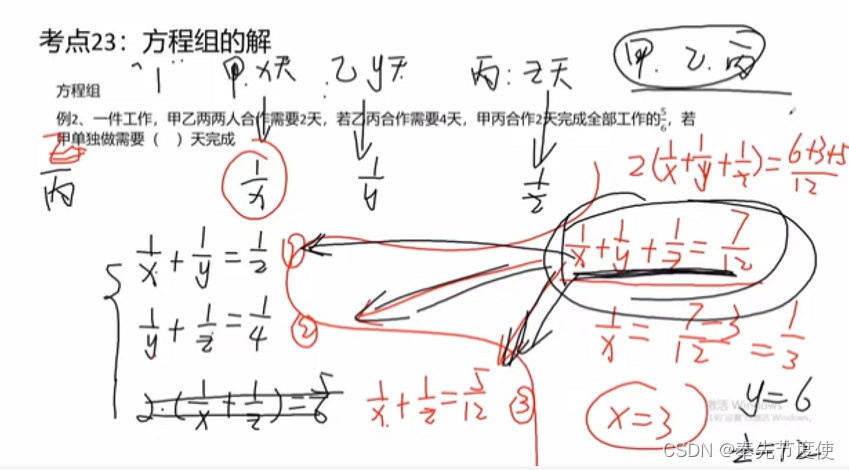
方程组的解
不等式的性质
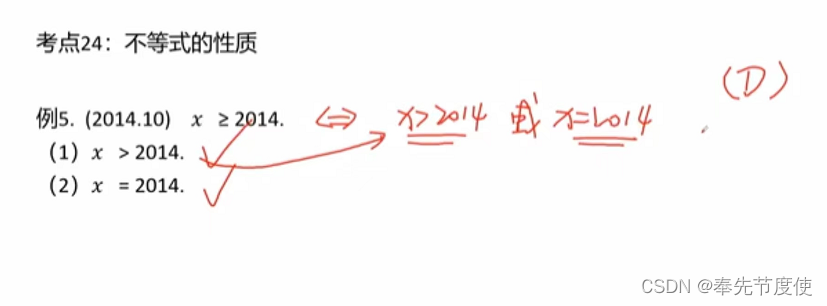
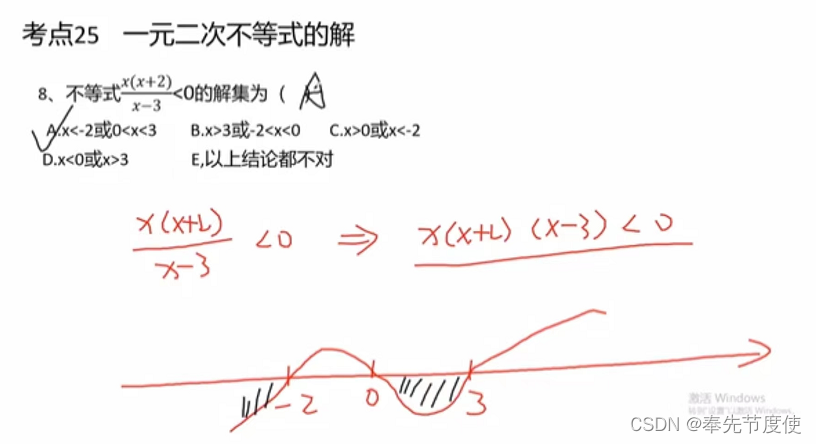
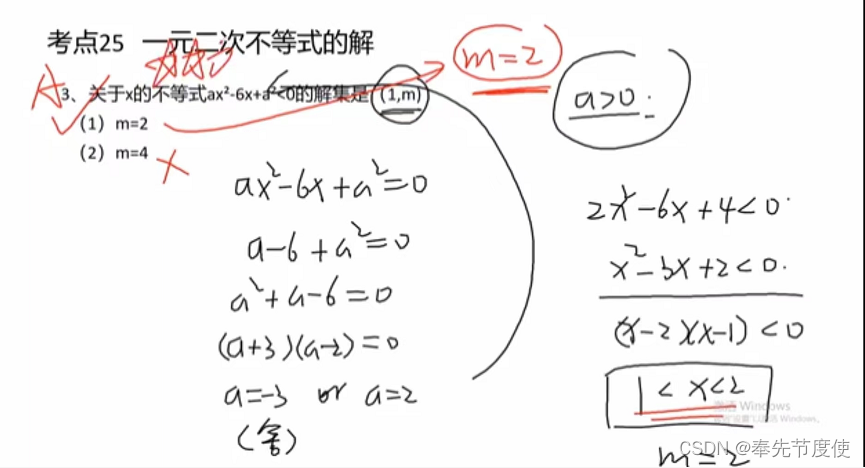
一元二次不等式的解
- 基本概念:不等式中含有一个未知数,未知数的次数为2,且不等式两边都是整式
- 解题思路:不等式看做方程式,然后结合抛物线法(数形结合思想)
- 一元二次不等式的解法

- 不等式解集的边界即为方程的根/零点/与x轴的交点

绝对值不等式(难点)
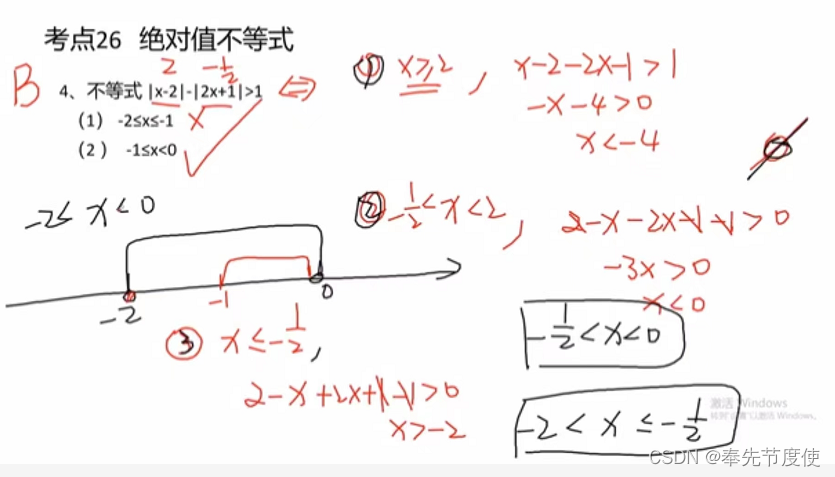
- 解题思路:解含有绝对值不等式的关键是去掉式子中的绝对值符号,常用方法如下
- 平方法:需要确保两边均为非负性才能平方
- 定义法分类讨论
- |f(x)|>f(x),如|x/x-1|>x/x-1
- f(x)>=0时|f(x)|=f(x)
- f(x)<0时|f(x)|=-f(x)
- |f(x)|<g(x)时需要注意g(x)自带定义域
- |f(x)|>f(x),如|x/x-1|>x/x-1
- 公式法
- |f(x)|<a,a>0时则有-a<f(x)<a
- |f(x)|>a,a>0时则有f(x)>a或者f(x)<-a


数列(平均2-3题)
数列相关定义
- 定义:数列是按照一定顺序排列着的一列数
- an与{an}概念不同,an表示数列的第n项,{an}表示数列
- 数列和集合区别
- 集合元素确定、无序、互异
- 数列元素确定、有序、可重复
- an与S(前n项和)关系
- an=S1(n=1)
- an=Sn=Sn-1(n>=2)
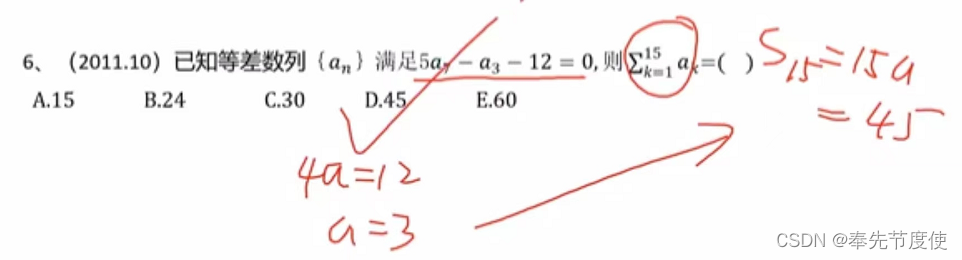
等差数列
- 定义:如果一个数列从第二项起,每一项与它前一项的差等于同一个常数
- 该常数为公差d,可正可负,可0,为0时表示常数项
- 通项公式
- an = a1 +(n-1)d
- an = am +(n-m)d 《=》d=an-am / n-m(n!=m)
- 扩展
- 常数列思想:题目中只有单一条件,此时将每个数列项看做常数项
- 等差中项/均值:如a,b,c为等差数列,则2b=a+c
- 等差数列前n项和公式
- sn=n(a1+an)/2 《=》sn=d/2n^2+(a1-d/2)n,即sn是关于n的二次函数(常数项为0)
- 即可推出d>0,Sn有最小值,d<0有最大值
- sn=An^2+Bn+C,若C=0则为等差数列,若C!=0则从第二项开始是等差数列
- sn=n(a1+an)/2 《=》sn=d/2n^2+(a1-d/2)n,即sn是关于n的二次函数(常数项为0)
- 等差数列连续几项之和构成的新数列仍然是等差数列,即Sn,S2n-Sn...
- 等差数列判定法
- 定义法:an-an-1=d,则为等差数列
- 通项公式法:an = Pn+q,则为等差数列
- 中项公式法:2an+1=an + an+2,则为等差数列
- 前n项和公式法:sn=An^2 + Bn,则为等差数列


等比数列
- 定义:如果一个数列从第二项起,每一项与它前一项的比值等于同一个常数
- 该常数为公比q,q!=0,当q=1时表示非0的常数列
- 通项公式
- an = a1 * q^n-1
- an = am * q^n-m
- 等比数列前n项和公式
- q!=1时, Sn=a1(1-q^n)/1-q=(a1-a1q^n)/1-q
- q=1时,Sn=na1
- q!=0且q!=1时,则Sn=A-Aq^n《=》Sn=A+Bq^n(A+B=0)
- 等比数列性质:若m+n=p+k,则am*an=ap*ak,特别的若m+n=2p,则am*an=ap^2
- 等比数列判定法
- 定义法:an+1/an=q,则为等比数列
- 通项公式法:an = cq^n,则为等比数列
- 中项公式法:an+1^2=an*an+2,则为等比数列
- 前n项和公式法:Sn=A-Aq^n,则为等比数列
数列综合


相关文章:

2024级199管理类联考之数学基础(上篇)
管理类考试介绍 管理综合200分,时间3小时 数学:75分/25题,是拉开差距的核心模块 问题求解题:15个,5选一条件充分性判断:10个,结合两个条件选择答案 条件一充分,条件二不充分:A条件一不充分,条件二充分:B条件一充分,条…...
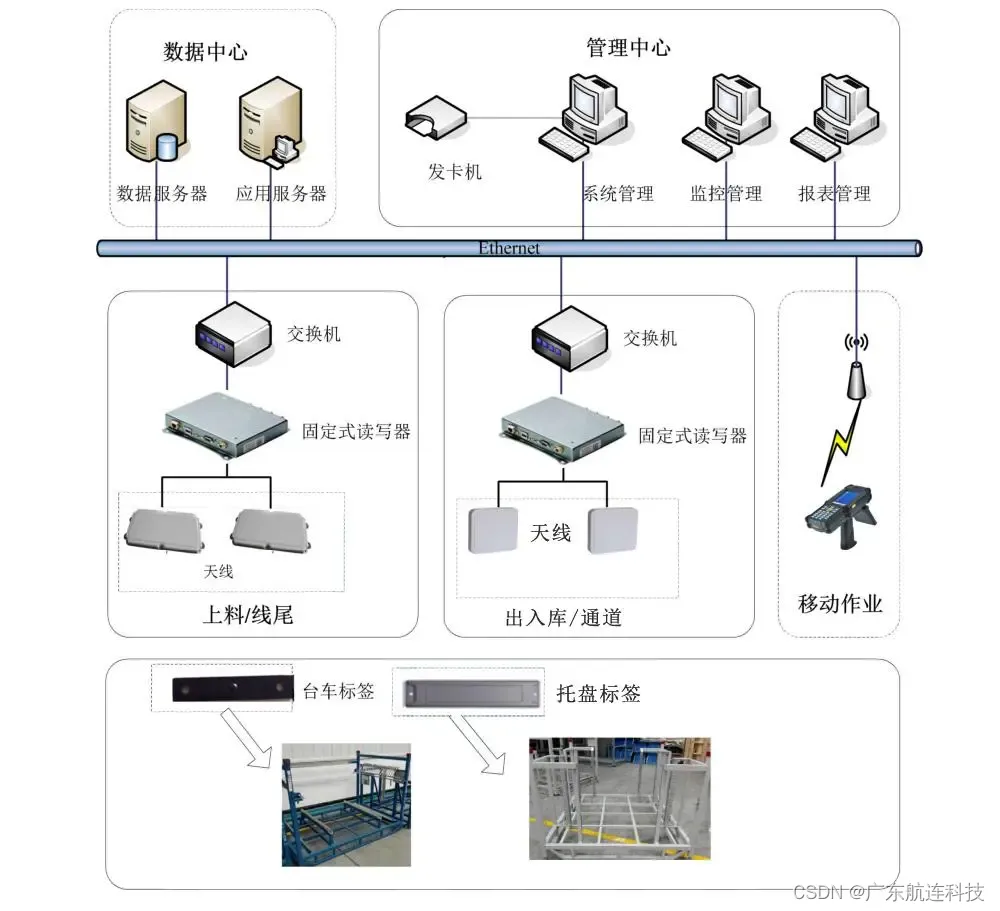
RFID技术引领汽车零部件加工新时代
RFID技术的兴起引领了汽车零部件加工领域的新时代,作为一种利用无线电频率进行自动识别的技术,RFID技术能够快速、准确地识别物体并获取相关数据,在汽车零部件加工中,RFID技术具有重要的应用价值,可以提高生产效率、降…...
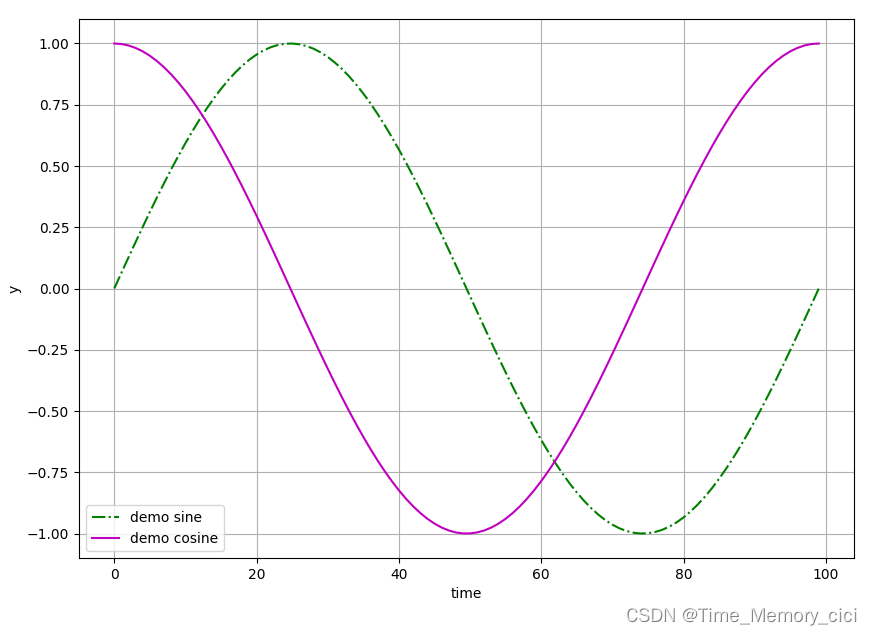
python中使用matplotlib绘图
一、背景 当我们在写python程序时,不可避免的需要将数据可视化,也就是绘制出数据的曲线图,以便我们更直观的观察数据间的变化,和方便对比。此时就要用到matplotlib库了。 matplotlib官方给出的定义是: 翻译过来也就是…...

Qt Creator 使用技巧
使用技巧 功能快捷键解释Switch Header/SourceF4在同名的头文件和源程序文件之间切换Follow Symbol Under CursorF2变量:跳转到声明;函数:声明和定义切换Refactor Rename Symbol Under CursorCtrlShiftR改名称,将替换所有用到这个符号的地方RefactorAdd Definition…...

来看看双阶段目标检测算法趴
🚀 作者 :“码上有钱” 🚀 文章简介 :AI-目标检测算法 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬简介 双阶段目标检测算法是一类深度学习算法,通常分为两个阶段来检测和识别图像中的…...
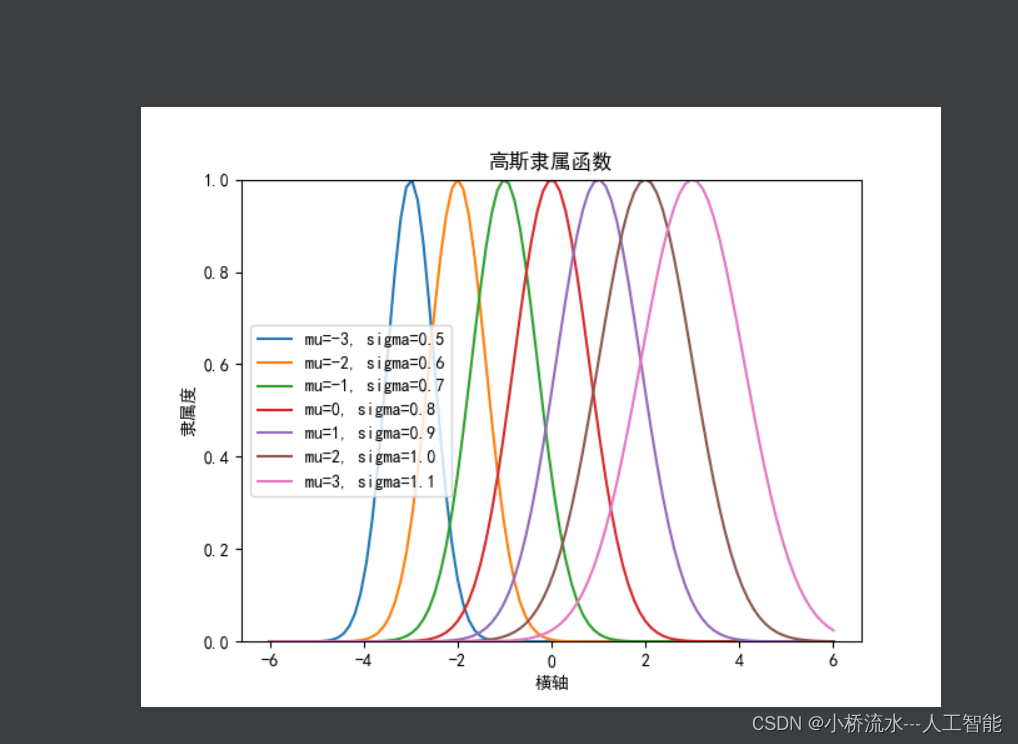
python利用matplotlib绘图,对于中文和负号不显示,显示方框“口口”完美解决办法!!
文章目录 一、问题展示二、问题分析三、解决办法四、结果展示 一、问题展示 二、问题分析 可以发现对中文,以及负号不显示。 三、解决办法 import matplotlib.pyplot as pltplt.rcParams[font.sans-serif] [usimHei] # 显示中文 plt.rcParams[axes.unicode_mi…...
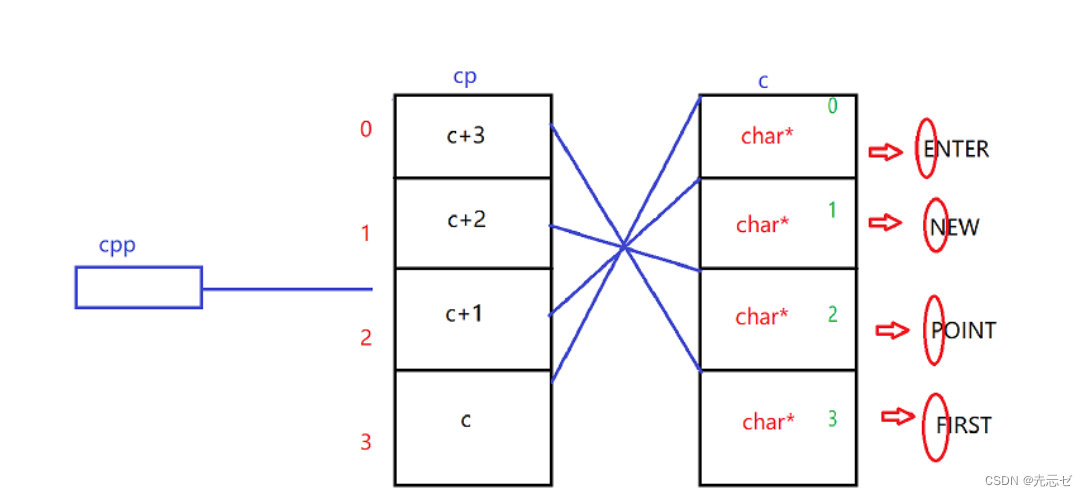
【数组及指针经典笔试题解析】
1.数组和指针笔试题 题目1 int main(){int a[5] { 1,2,3,4,5};int * ptr (int * )(&a 1);printf("%d,%d",*(a 1),*(ptr - 1));return 0;}图文解析: int * ptr …...
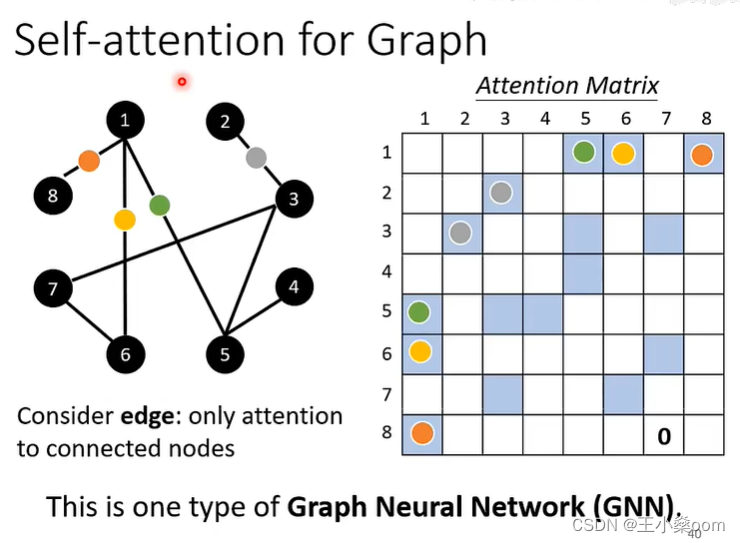
Transformer学习-self-attention
这里写自定义目录标题 Self-attentionMulti-head self-attention用self-attention解决其他问题 Self-attention 用Wq、Wk、Wv分别乘输入向量得到q、k、v向量 用每个q向量乘所有的k向量得到对应项的attention,即用每项的query向量去匹配所有的key向量,得…...

Spring Boot:利用JPA进行数据库的增改
目录 JPA介绍Service接口Service和Autowired示例代码 Dao数据库操作层Repository示例代码 控制器文件示例代码-增加增加成功示例代码-修改修改成功 JPA介绍 JPA(Javaa Persistence API)一种用于持久化 Java 对象到关系型数据库的标准规范。它提供了一种统一的方式来…...
列表的增删改查和遍历
任务概念 什么是任务 任务是一个参数为指针,无法返回的函数,函数体为死循环不能返回任务的实现过程 每个任务是独立的,需要为任务分别分配栈称为任务栈,通常是预定义的全局数组,也可以是动态分配的一段内存空间&#…...

获取网卡上的IP、网关及DNS信息,获取最佳路由,遍历路由表中的条目(附源码)
VC常用功能开发汇总(专栏文章列表,欢迎订阅,持续更新...)https://blog.csdn.net/chenlycly/article/details/124272585C软件异常排查从入门到精通系列教程(专栏文章列表,欢迎订阅,持续更新...&a…...
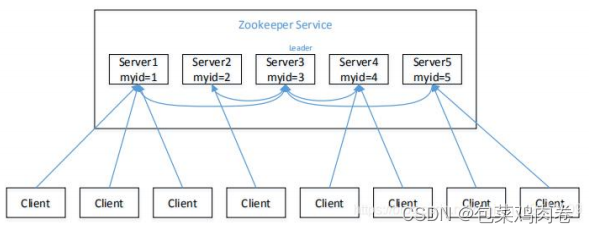
保姆级 -- Zookeeper超详解
1. Zookeeper 是什么(了解) Zookeeper 是一个 分布式协调服务 的开源框架, 主要用来解决分布式集群中应用系统的一致性问题, 例如怎样避免同时操作同一数据造成脏读的问题. ZooKeeper 本质上是 一个分布式的小文件存储系统 . 提供基于类似于文件系统的目录树方式的数据存储, …...

【通意千问】大模型GitHub开源工程学习笔记(2)--使用Qwen进行推理的示例代码解析,及transformers的库使用
使用Transformers来使用模型 如希望使用Qwen-chat进行推理,所需要写的只是如下所示的数行代码。请确保你使用的是最新代码,并指定正确的模型名称和路径,如Qwen/Qwen-7B-Chat和Qwen/Qwen-14B-Chat 这里给出了一段代码 from transformers import AutoModelForCausalLM, Aut…...

从0开始python学习-23.selenium 常见鼠标的操作
注意:必须创建一个事件链对象(ActionChains);最后鼠标事件链完成之后一定要进行事务提交perform()(如果事件链不提交那么所有的鼠标事件都不会执行) 1. 左键单击:click()…...

电气基础——电源、变压器、接触器、断路器、线缆
目录 1.电源 2.变压器 三项电和2相电的转换 3.接触器 4.断路器 5.线缆 1.电源 2.变压器 三项电和2相电的转换 三相电转为2相电 1.变压器 2.相位移转换器 3.电容器 两相电变不了三相电。但是两相电可以通过电容移相后带动三相电机 零线,地线Nÿ…...

步力宝科技爆款产品定位,开创智能物联网新商业
数据显示,中国处于 “亚健康”状态人口数量约占总人口的70%,亚健康是一种临界状态,指介于健康和疾病之间的状态。亚健康是一个动态演变的过程,既有向慢病发展的趋势,也能通过合理的干预使人体重返健康状态,…...
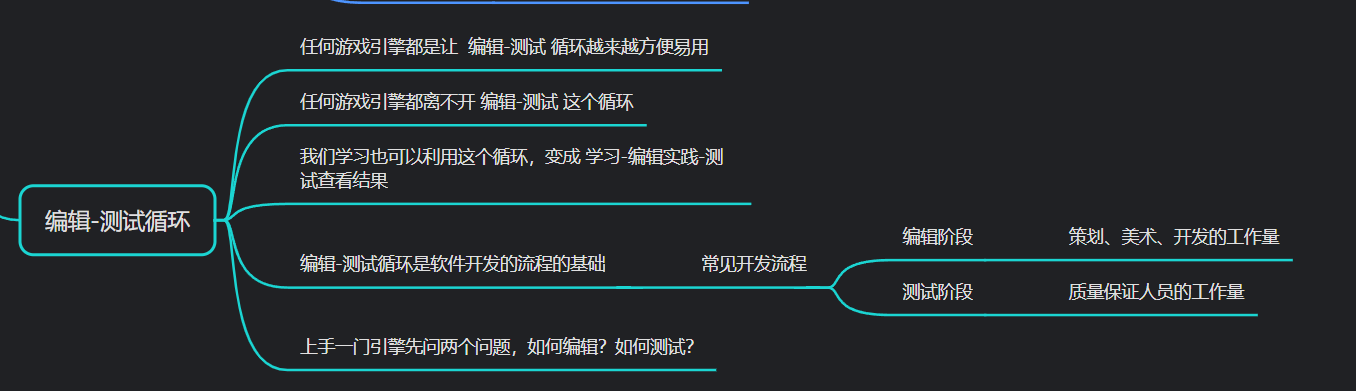
凉鞋的 Unity 笔记 105. 第一个通识:编辑-测试 循环
105. 第一个通识:编辑-测试 循环 在这一篇,我们简单聊聊此教程中所涉及的一个非常重要的概念:循环。 我们在做任何事情都离不开某种循环,比如每天的 24 小时循环,一日三餐循环,清醒-睡觉循环。 在学习一…...
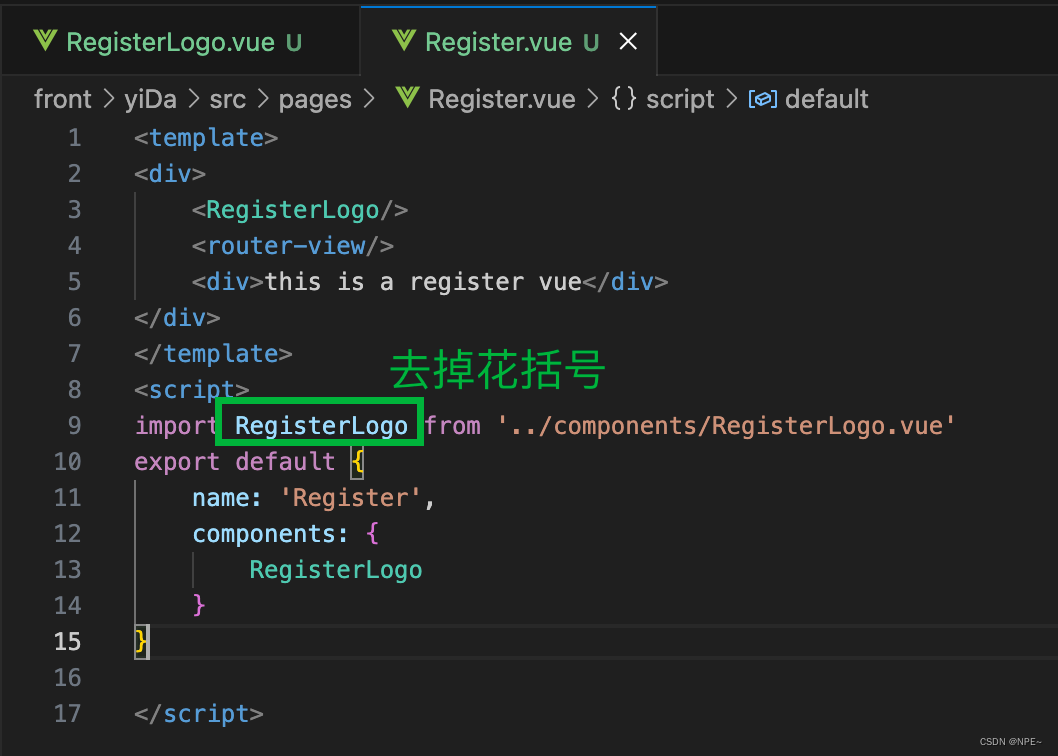
Bug:elementUI样式不起作用、Vue引入组件报错not found等(Vue+ElementUI问题汇总)
前端问题合集:VueElementUI 1. Vue引用Element-UI时,组件无效果解决方案 前提: 已经安装好elementUI依赖 //安装依赖 npm install element-ui //main.js中导入依赖并在全局中使用 import ElementUI from element-ui Vue.use(ElementUI)如果此…...
)
【大麦小米学量化】使用文心一言AI编写股票量化交易策略代码(含演示代码和进阶演示)
文章目录 AI是个宝前言一、文心一言是什么?二、让AI根据策略写出代码1. 策略提示词2. AI给出的策略代码及说明 三、进阶调试总结 AI是个宝 小米听说百度开放了文心一言AI,好奇的跑去问大麦:“文心一言都放开了,什么代码都可以写&a…...
)
软考 系统架构设计师系列知识点之软件架构风格(1)
这个十一注定是一个不能放松、保持“紧”的十一。由于报名了全国计算机技术与软件专业技术资格(水平)考试,11月4号就要考试,因此8天长假绝不能荒废,必须要好好利用起来。现在将各个核心知识点一一进行提炼并做记录。 所…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
