【算法训练-贪心算法 一】买卖股票的最佳时机II
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【贪心算法】,使用【数组】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为:目标公司+最近一年+出现频率排序,由高到低的去牛客TOP101去找,只有两个地方都出现过才做这道题(CodeTop本身汇聚了LeetCode的来源),确保刷的题都是高频要面试考的题。

名曲目标题后,附上题目链接,后期可以依据解题思路反复快速练习,题目按照题干的基本数据结构分类,且每个分类的第一篇必定是对基础数据结构的介绍。
买卖股票的最佳时机II【MID】
难度升级,股票可以反复买卖,不是只买卖一次,还是求最大收益
题干
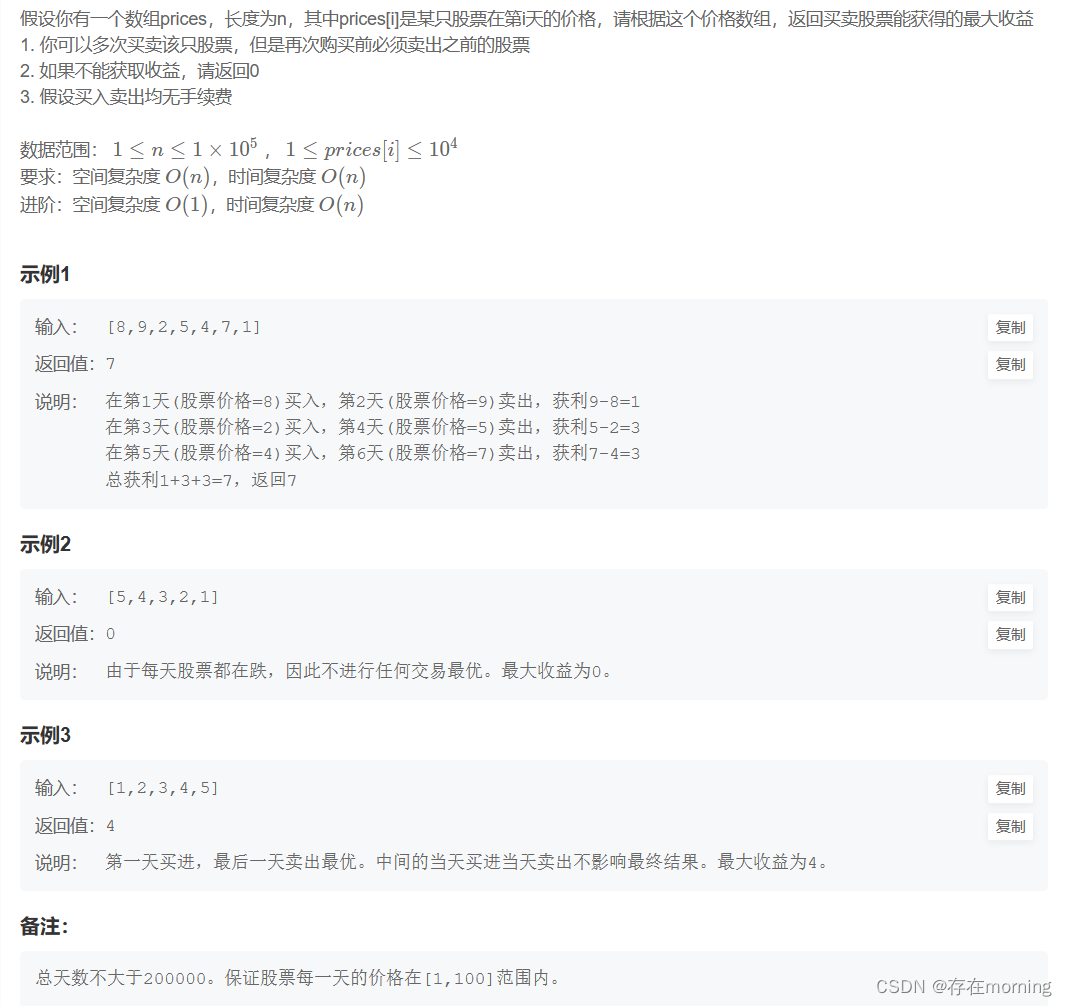
解题思路
整体使用贪心算法实现:
- 对于单独交易日: 设今天价格 p1 、明天价格 p2 ,则今天买入、明天卖出可赚取金额 p2−p1(负值代表亏损)。
- 对于连续上涨交易日: 设此上涨交易日股票价格分别为 p1,p2,…,pn,则第一天买最后一天卖收益最大,即 pn−p1 ;等价于每天都买卖,即 pn−p1=(p2−p1)+(p3−p2)+…+(pn−pn−1)p_n - p_1=(p_2 - p_1)+(p_3 - p_2)+…+(p_n - p_{n-1})
- 对于连续下降交易日: 则不买卖收益最大,即不会亏钱。
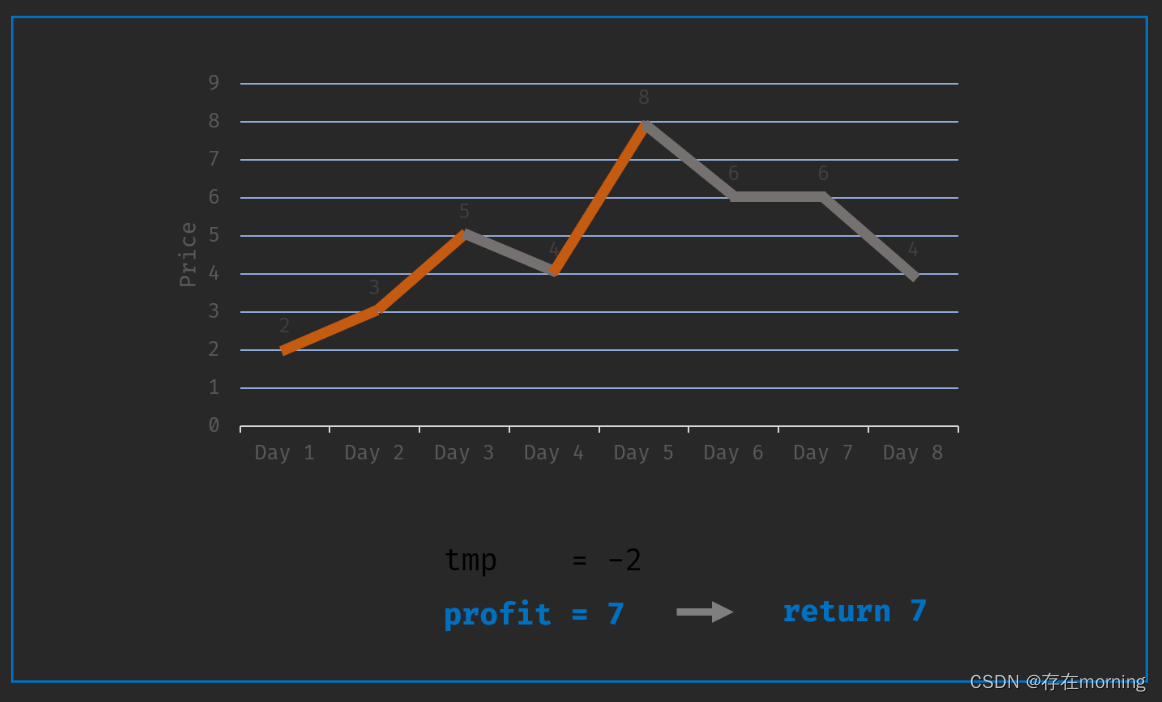
遍历整个股票交易日价格列表 price,并执行贪心策略:所有上涨交易日都买卖(赚到所有利润),所有下降交易日都不买卖(永不亏钱)
- 设 tmp 为第 i-1 日买入与第 i 日卖出赚取的利润,即 tmp = prices[i] - prices[i - 1] ;
- 当该天利润为正 tmp > 0,则将利润加入总利润 profit;当利润为 0 或为负,则直接跳过;
- 遍历完成后,返回总利润 profit
代码实现
给出代码实现基本档案
基本数据结构:数组
辅助数据结构:无
算法:贪心算法
技巧:无
其中数据结构、算法和技巧分别来自:
- 10 个数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
- 10 个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
- 技巧:双指针、滑动窗口、中心扩散
当然包括但不限于以上
import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** 计算最大收益* @param prices int整型一维数组 股票每一天的价格* @return int整型*/public int maxProfit (int[] prices) {// 1 定义总利润int maxProfit = 0;for (int i = 1; i < prices.length; i++) {// 2 获取当天利润int curProfit = prices[i] - prices[i - 1];// 3 只有当天利润为正值才计入总利润maxProfit = Math.max(curProfit, 0) + maxProfit;}return maxProfit;}
}
复杂度分析
时间复杂度:遍历了一遍数组,所以时间复杂度为O(N)
空间复杂度:没有借助额外空间,空间复杂度为O(1)
拓展知识:动态规划与贪心算法
动态规划
动态规划(Dynamic Programming,简称DP)是一种解决复杂问题的算法设计技术,常用于优化问题和组合问题的求解。它通过将原问题分解成子问题,并保存子问题的解,以避免重复计算,从而提高算法的效率。动态规划通常用于解决具有重叠子问题和最优子结构性质的问题。
动态规划的基本思想可以总结为以下几个步骤:
-
定义问题的状态:首先要明确定义问题的状态,这些状态可以用来描述问题的各种情况。
-
找到状态转移方程:状态转移方程描述了问题之间的联系,即如何从一个状态转移到另一个状态。这通常涉及到问题的递归关系,通过这个关系可以从较小规模的子问题得到更大规模的问题的解。
-
初始化状态:确定初始状态的值,这通常是问题规模最小的情况下的解。
-
自底向上或自顶向下求解:动态规划可以采用自底向上(Bottom-Up)或自顶向下(Top-Down)的方式求解问题。自底向上是从最小的状态开始逐步计算,直到得到最终问题的解;自顶向下是从最终问题开始,递归地计算子问题的解,直到达到最小状态。
-
根据问题的要求,从状态中找到最终解。
动态规划常见的应用领域包括:
-
最长公共子序列问题:在两个序列中找到一个最长的共同子序列,用于比较字符串相似性。
-
背包问题:在给定一定容量的背包和一组物品的情况下,选择一些物品放入背包,使得物品的总价值最大或总重量不超过背包容量。
-
最短路径问题:求解图中两点之间的最短路径,如Dijkstra算法和Floyd-Warshall算法。
-
硬币找零问题:给定一组硬币面额和一个目标金额,找到使用最少数量的硬币组合成目标金额。
-
斐波那契数列问题:求解斐波那契数列的第n个数,通过动态规划可以避免重复计算。
动态规划是一种强大的问题求解方法,但它并不适用于所有类型的问题。在使用动态规划时,需要仔细分析问题的性质,确保问题具有重叠子问题和最优子结构性质,以确保动态规划算法能够有效地解决问题。
贪心算法
贪心算法(Greedy Algorithm)是一种常用的问题求解策略,通常用于解决最优化问题,如最短路径、最小生成树、背包问题等。贪心算法的基本思想是每一步都选择当前状态下的最优解,而不考虑全局的最优解,希望通过局部最优的选择最终达到全局最优。贪心算法通常是一种高效的方法,但并不是所有问题都适合使用贪心算法,因为有些问题的最优解不一定可以通过贪心选择得到。
贪心算法的一般步骤如下:
-
定义问题的优化目标,明确问题的约束条件。
-
从问题的初始状态开始,通过一系列选择,每次选择局部最优解,更新当前状态。
-
检查是否满足问题的约束条件和终止条件。如果不满足,则回到第2步继续选择;如果满足,则算法结束。
-
对于某些问题,需要证明贪心选择的局部最优解确实能够导致全局最优解,这需要数学证明或者举出反例。
以下是一些常见的问题,可以使用贪心算法解决:
-
最小生成树问题:如Kruskal算法和Prim算法用于寻找无向图中的最小生成树。
-
最短路径问题:如Dijkstra算法用于寻找图中两点之间的最短路径。
-
背包问题:如分数背包问题和0/1背包问题,可以使用贪心算法进行求解。
-
活动选择问题:如贪心选择活动安排最多的问题,可以使用贪心算法求解。
需要注意的是,并非所有问题都适合使用贪心算法,因为有些问题的最优解可能需要全局搜索或者动态规划等其他算法。因此,在应用贪心算法之前,需要仔细分析问题的特点和性质,以确定贪心算法是否合适。
动态规划与贪心算法区别
动态规划(Dynamic Programming)和贪心算法(Greedy Algorithm)都是常见的问题求解策略,但它们在问题求解时有很大的区别,适用于不同类型的问题和场景。
区别:
-
最优子结构性质:
- 动态规划:动态规划问题通常具有最优子结构性质,即全局最优解可以通过子问题的最优解来构造。动态规划通常涉及到将问题划分为重叠的子问题,然后利用这些子问题的解来构建全局最优解。
- 贪心算法:贪心算法通常涉及到每一步选择当前状态下的最优解,但不一定具有最优子结构性质。贪心算法通常是通过一系列局部最优选择来达到全局最优,但不能保证一定能够得到全局最优解。
-
选择的灵活性:
- 动态规划:在动态规划中,可以在每个子问题中考虑多种选择,并计算每种选择的代价或价值,然后选择最优的。通常需要一个状态转移方程来描述问题的子结构和递归关系。
- 贪心算法:贪心算法在每一步都选择当前状态下的最优解,不考虑其他选择的影响。它通常适用于问题具有"贪心选择性质"的情况,即通过局部最优选择能够得到全局最优解。
问题解决场景:
-
动态规划适用场景:
- 当问题的最优解可以通过子问题的最优解来构造时,通常使用动态规划。典型问题包括:
- 最短路径问题(如Dijkstra算法)
- 最长公共子序列问题
- 背包问题(如0/1背包问题)
- 编辑距离问题
- 需要存储和重用子问题的解,通常使用表格或数组来实现。
- 当问题的最优解可以通过子问题的最优解来构造时,通常使用动态规划。典型问题包括:
-
贪心算法适用场景:
- 当问题具有贪心选择性质,即通过每一步的局部最优选择能够达到全局最优时,可以使用贪心算法。典型问题包括:
- 最小生成树问题(如Prim算法和Kruskal算法)
- 哈夫曼编码问题
- 活动选择问题
- 货币找零问题
- 贪心算法通常更简单和高效,但不能解决所有问题,因为它没有全局的视野。
- 当问题具有贪心选择性质,即通过每一步的局部最优选择能够达到全局最优时,可以使用贪心算法。典型问题包括:
总之,动态规划和贪心算法是两种不同的问题求解策略,根据问题的特性和要求选择合适的算法非常重要。有些问题可以同时使用这两种策略的思想,即使用贪心算法的局部最优性来设计动态规划的状态转移方程。
相关文章:

【算法训练-贪心算法 一】买卖股票的最佳时机II
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【贪心算法】,使用【数组】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为&…...

单阶段目标检测与双阶段目标检测的联系与区别
🚀 作者 :“码上有钱” 🚀 文章简介 :AI-目标检测算法 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬简介 双阶段目标检测算法与单阶段目标检测算法在工作原理和性能方面存在一些相似与差异之处。下…...

Mysql技术文档--设计表规范式-一次性扫盲
阿丹: 在设计表的时候经常出现一些问题,其实自己很清楚就是因为在设计表的时候没有规范。导致后期加表的时候出现了问题。所以趁着这个假期卷一卷。同时只有在开始的时候 几大范式 在关系型数据库中,数据表设计的基本原则、规则就称为范式。…...

python socket 传输opencv读取的图像
python socket网络编程 将ros机器人摄像头捕捉的画面在上位机实时显示,需要用到socket网络编程,提供了TCP和UDP两种方式 TCP服务器端代码: 创建TCP套接字: s socket(AF_INET, SOCK_STREAM) 创建了一个TCP套接字。SOCK_STREAM 表示这是一个TCP套接字&…...
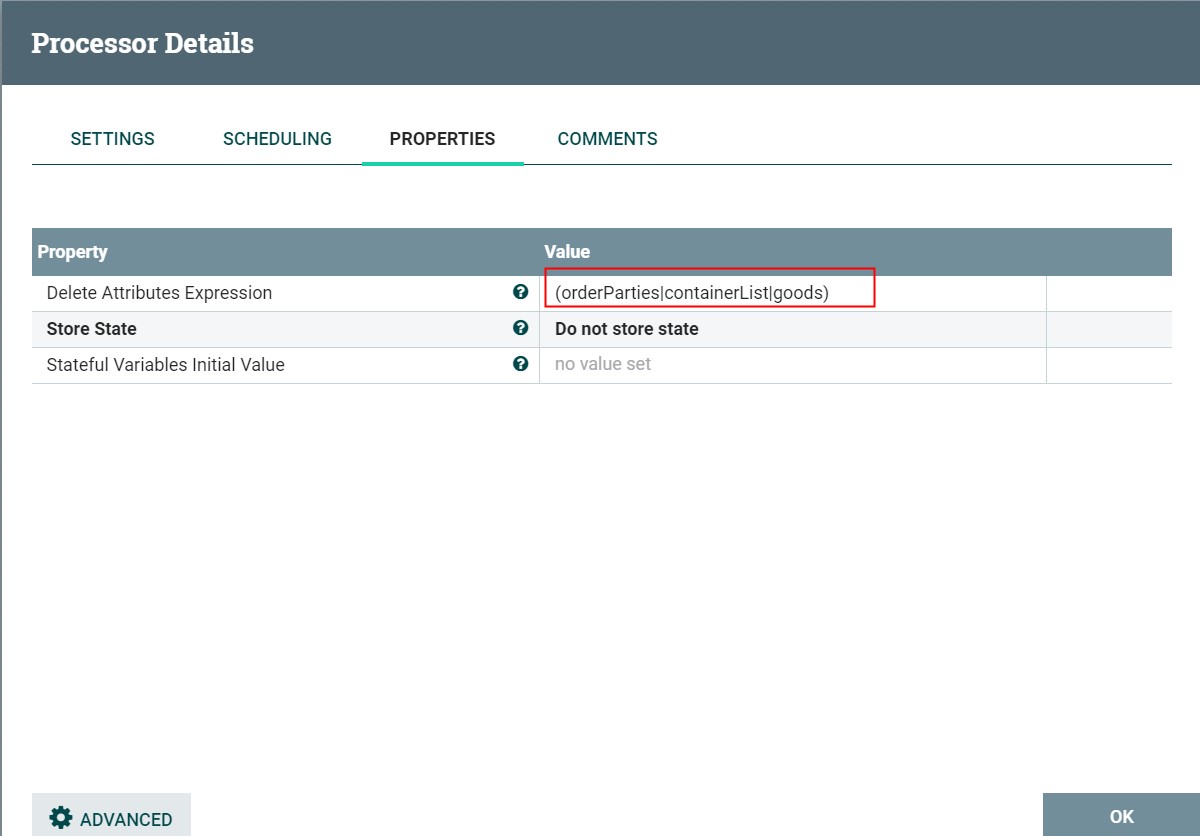
APACHE NIFI学习之—UpdateAttribute
UpdateAttribute 描述: 通过设置属性表达式来更新属性,也可以基于属性正则匹配来删除属性 标签: attributes, modification, update, delete, Attribute Expression Language, state, 属性, 修改, 更新, 删除, 表达式 参数: 如下列表中,必填参数则…...
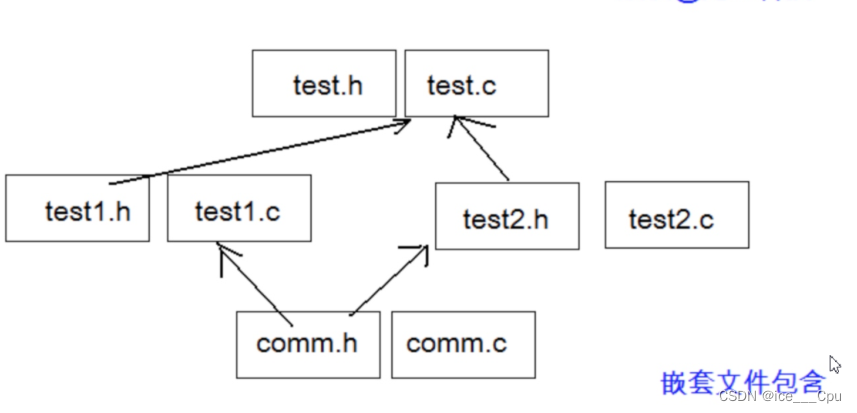
BIT-7文件操作和程序环境(16000字详解)
一:文件 1.1 文件指针 每个被使用的文件都在内存中开辟了一个相应的文件信息区,用来存放文件的相关信息(如文件的名字,文件状态及文件当前的位置等)。这些信息是保存在一个结构体变量中的。该结构体类型是有系统声明…...

冥想第九百二十八天
1.今天周三,今天晚上日语课上了好久,天气也不好, 2.项目上全力以赴的一天。 3.感谢父母,感谢朋友感谢家人,感谢不断进步的自己。...

深入浅出,SpringBoot整合Quartz实现定时任务与Redis健康检测(一)
目录 前言 环境配置 Quartz 什么是Quartz? 应用场景 核心组件 Job JobDetail Trigger CronTrigger SimpleTrigger Scheduler 任务存储 RAM JDBC 导入依赖 定时任务 销量统计 Redis检测 使用 编辑 注意事项 前言 在悦享校园1.0中引入了Quart…...
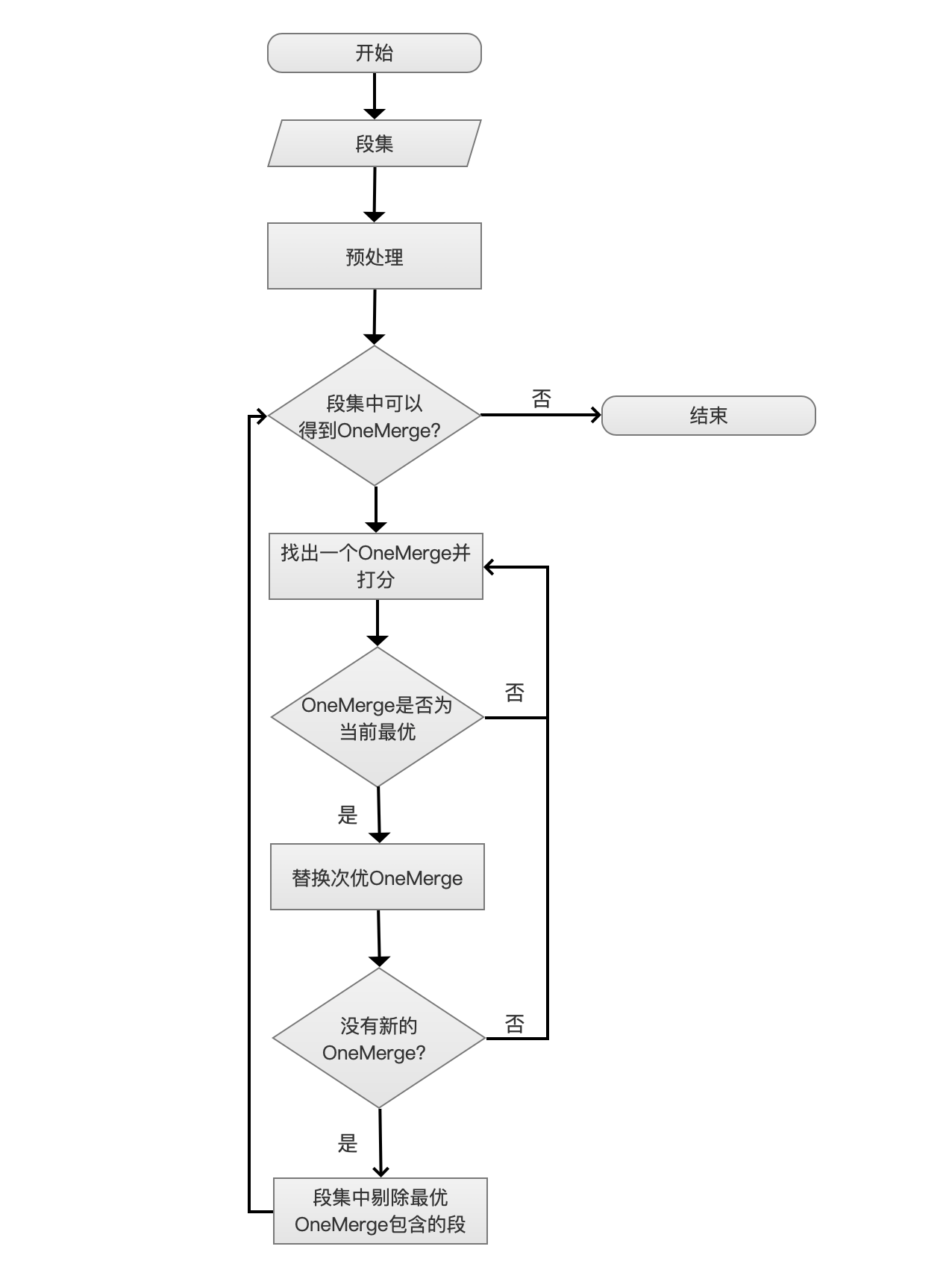
Lucene-MergePolicy详解
简介 该文章基于业务需求背景,因场景需求进行参数调优,下文会尽可能针对段合并策略(SegmentMergePolicy)的全参数进行说明。 主要介绍TieredMergePolicy,它是Lucene4以后的默认段的合并策略,之前采用的合并…...

数据的加解密
文章目录 分类特点业务的使用补充 分类 对称加密算法非对称加密算法 特点 对称加密算法 : 加密效率高 !加密和解密都使用同一款密钥 但是有一个问题 : 密钥如何从服务端发给客户端? (假如你直接先将密钥发给对方,要是在过程中被黑客技术破解了,那后面的消息也就泄漏了) (后…...

【Spring】更简单的读取和存储对象
更简单的读取和存储对象 一. 存储 Bean 对象1. 前置工作:配置扫描路径2. 添加注解存储 Bean 对象Controller(控制器存储)Service(服务存储)Repository(仓库存储)Component(组件存储&…...
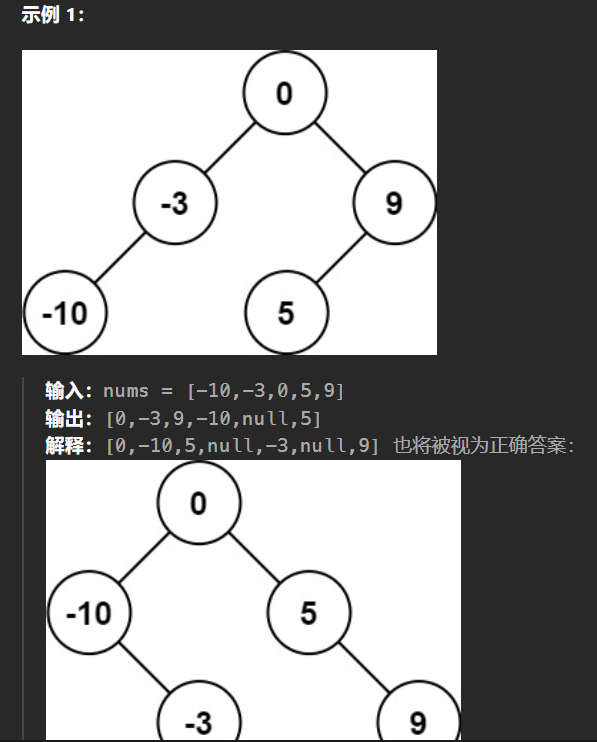
【LeetCode热题100】--108.将有序数组转换为二叉搜索树
108.将有序数组转换为二叉搜索树 给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。 高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。 二叉搜索树的中序遍历是升序…...

Redis学习笔记(下):持久化RDB、AOF+主从复制(薪火相传,反客为主,一主多从,哨兵模式)+Redis集群
十一、持久化RDB和AOF 持久化:将数据存入硬盘 11.1 RDB(Redis Database) RDB:在指定的时间间隔内将内存中的数据集快照写入磁盘,也就是行话讲的Snapshot快照,它恢复时是将快照文件直接读到内存里。 备份…...

【智能家居项目】裸机版本——设备子系统(LED Display 风扇)
🐱作者:一只大喵咪1201 🐱专栏:《智能家居项目》 🔥格言:你只管努力,剩下的交给时间! 输入子系统中目前仅实现了按键输入,剩下的网络输入和标准输入在以后会逐步实现&am…...

[Linux]记录plasma-wayland下无法找到HDMI接口显示器的问题解决方案
内核:Linux 6.5.5-arch1-1 Plasma 版本:5.27.8 窗口系统:Wayland 1 问题 在前些时候置入了一块显示器,接口较多,有 HDMI 接口,type-C 接口。在 X11 中可以找到外接显示器,但是卡顿明显…...

【计算机网络】高级IO之select
文章目录 1. 什么是IO?什么是高效 IO? 2. IO的五种模型五种IO模型的概念理解同步IO与异步IO整体理解 3. 阻塞IO4. 非阻塞IOsetnonblock函数为什么非阻塞IO会读取错误?对错误码的进一步判断检测数据没有就绪时,返回做一些其他事情完整代码myt…...

如何设计一个高效的应用缓冲区【一个动态扩容的buffer类】
文章目录 前言一、为什么需要设计应用层缓冲区必须要有 output buffer目的问题output buffer的解决方案: 必须要有 input buffer总结 二、设计要点三、buffer设计思路基础函数关于iovec与readv readfd如何实现动态扩容 问题 前言 在上一个博客,我们介绍…...

图像处理初学者导引---OpenCV 方法演示项目
OpenCV 方法演示项目 项目地址:https://github.com/WangQvQ/opencv-tutorial 项目简介 这个开源项目是一个用于演示 OpenCV 方法的工具,旨在帮助初学者快速理解和掌握 OpenCV 图像处理技术。通过这个项目,你可以轻松地对图像进行各种处理&a…...
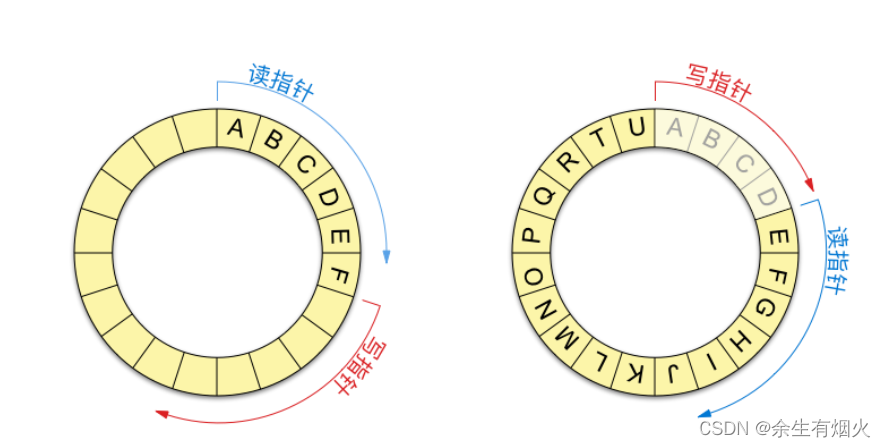
管道-匿名管道
一、管道介绍 管道(Pipe)是一种在UNIX和类UNIX系统中用于进程间通信的机制。它允许一个进程的输出直接成为另一个进程的输入,从而实现数据的流动。管道是一种轻量级的通信方式,用于协调不同进程的工作。 1. 创建和使用管道&#…...

【JavaEE基础学习打卡08】JSP之初次认识say hello!
目录 前言一、JSP技术初识1.动态页面2.JSP是什么3.JSP特点有哪些 二、JSP运行环境配置1.JDK安装2.Tomcat安装 三、编写JSP1.我的第一个JSP2.JSP执行过程3.在IDEA中开发JSP 总结 前言 📜 本系列教程适用于JavaWeb初学者、爱好者,小白白。我们的天赋并不高…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
