栈的应用场景(三)
最小栈
- 1.题目
- 2.画图分析
- 3.代码实现
1.题目

2.画图分析


3.代码实现
package Stack;import java.util.Stack;
public class MinStack {private Stack <Integer> stack;private Stack <Integer> MinStack;public MinStack() {stack = new Stack<>();MinStack = new Stack<>();}public void push(int val) {//普通栈只要是元素都得放//最小栈 如果为空,放元素.如果不为空且要放的元素比栈顶元素小,也要放stack.push(val);if(MinStack.empty()){MinStack.push(val);}else{int peek = MinStack.peek();if(val <= peek){MinStack.push(val);}}}public void pop() {int val = stack.pop();//如果最小栈不为空if(!MinStack.empty()){if(val == MinStack.peek()){MinStack.pop();}}}//获取普通栈的栈顶public int top() {return stack.peek();}public int getMin() {if(!MinStack.empty()){return MinStack.peek();}return -1;}
}相关文章:

栈的应用场景(三)
最小栈 1.题目2.画图分析3.代码实现 1.题目 2.画图分析 3.代码实现 package Stack;import java.util.Stack; public class MinStack {private Stack <Integer> stack;private Stack <Integer> MinStack;public MinStack() {stack new Stack<>();MinStack …...

leetCode 45.跳跃游戏 II 贪心算法
45. 跳跃游戏 II - 力扣(LeetCode) 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 &…...
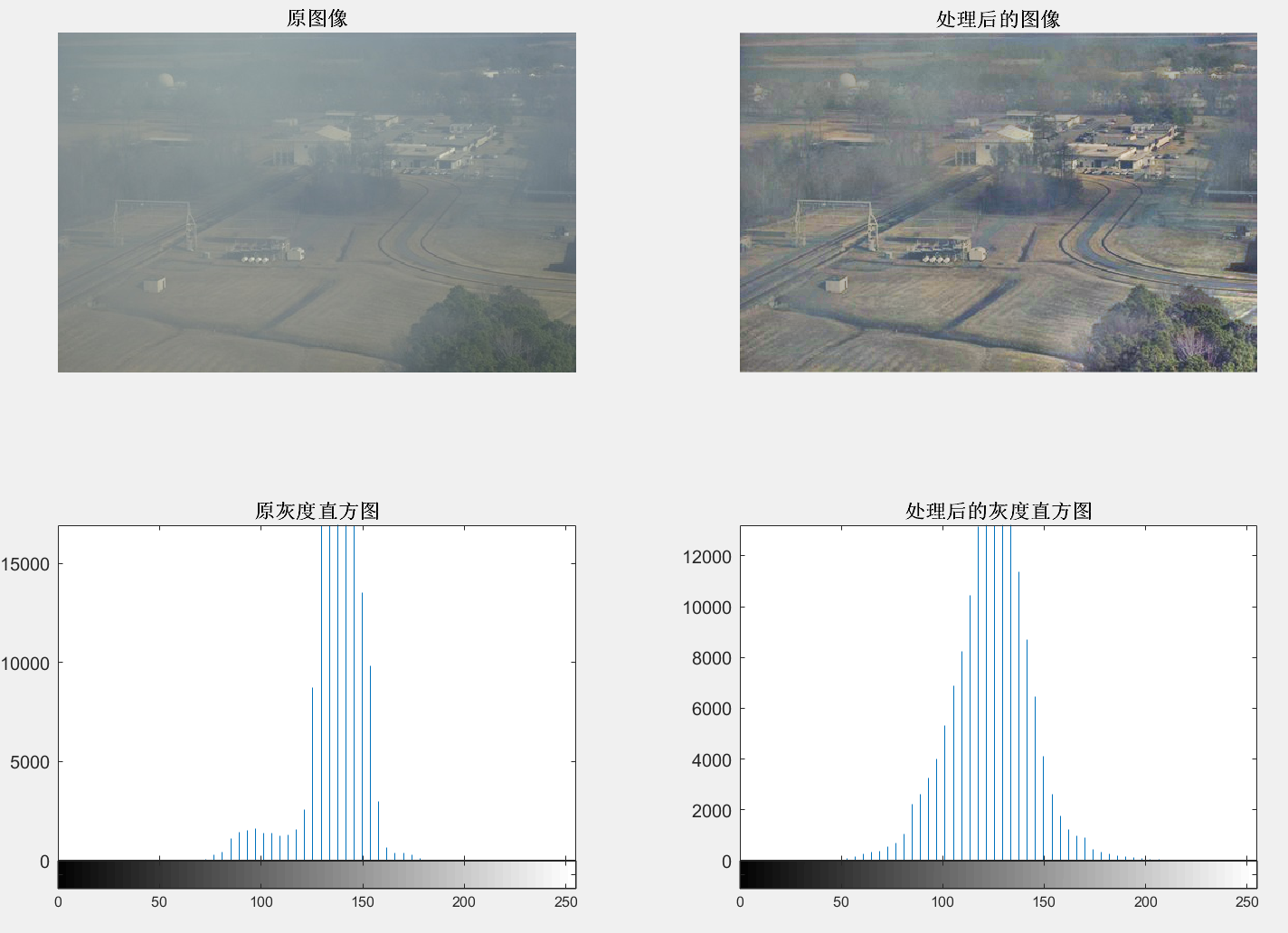
【MATLAB-基于直方图优化的图像去雾技术】
【MATLAB-基于直方图优化的图像去雾技术】 1 直方图均衡2 程序实现3 局部直方图处理 1 直方图均衡 直方图是图像的一种统计表达形式。对于一幅灰度图像来说,其灰度统计直方图可以反映该图像中不同灰度级出现的统计情况。一般而言,图像的视觉效果和其直方…...
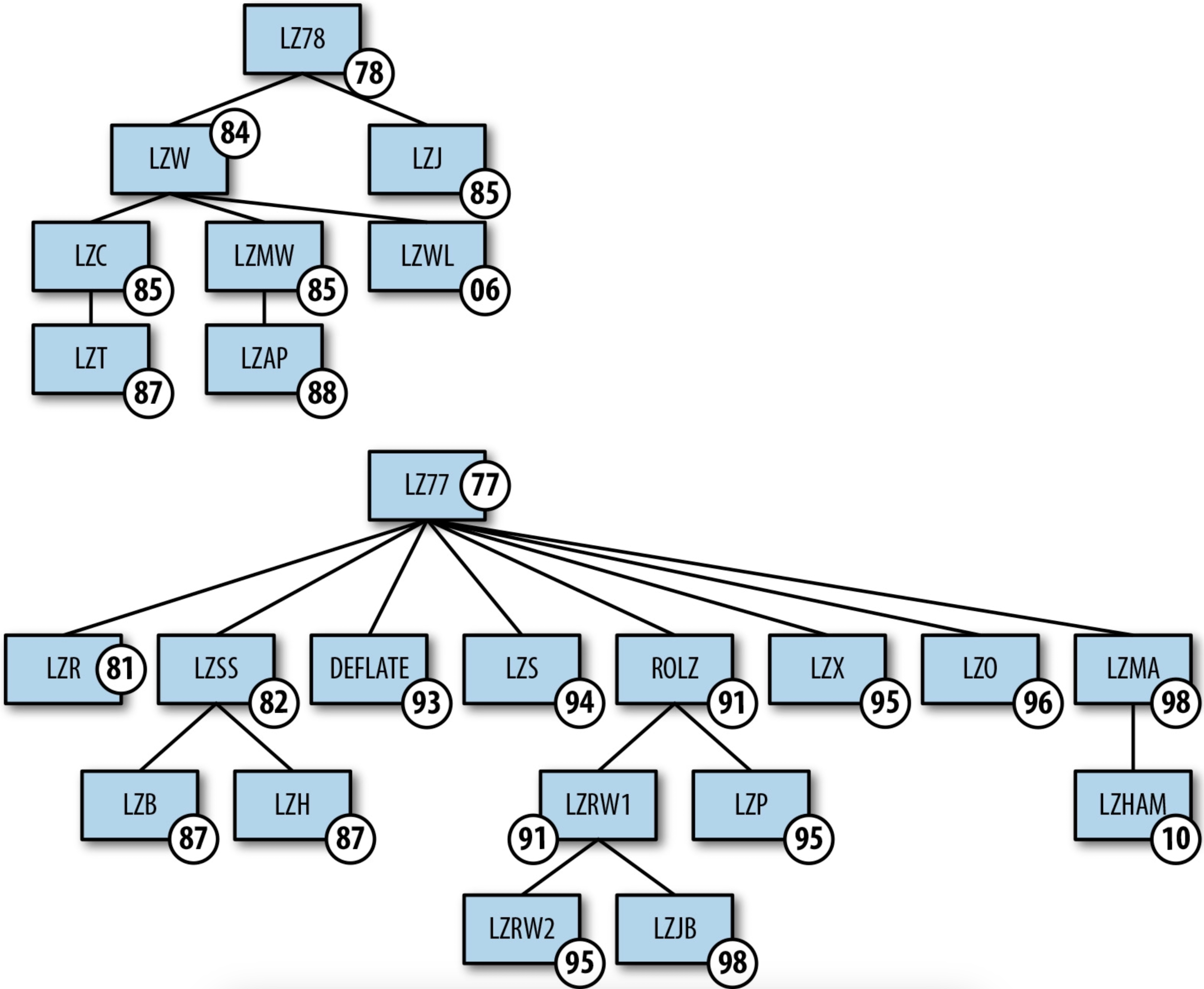
读书笔记|《数据压缩入门》—— 柯尔特·麦克安利斯 亚历克斯·海奇
前言:在接触文本隐写研究领域时了解到这本书。本书可算作《数据压缩》的入门书籍之一,这本书对熵编码、变长编码、统计编码、自适应统计编码、字典编码、上下文编码等常用编码方式的定义及来源进行介绍,对不同场景下不同格式的压缩数据有针对…...
)
Pandas进阶修炼120题-第五期(一些补充,101-120题)
目录 往期内容:第一期:Pandas基础(1-20题)第二期:Pandas数据处理(21-50题)第三期:Pandas金融数据处理(51-80题)第四期:当Pandas遇上NumPy…...
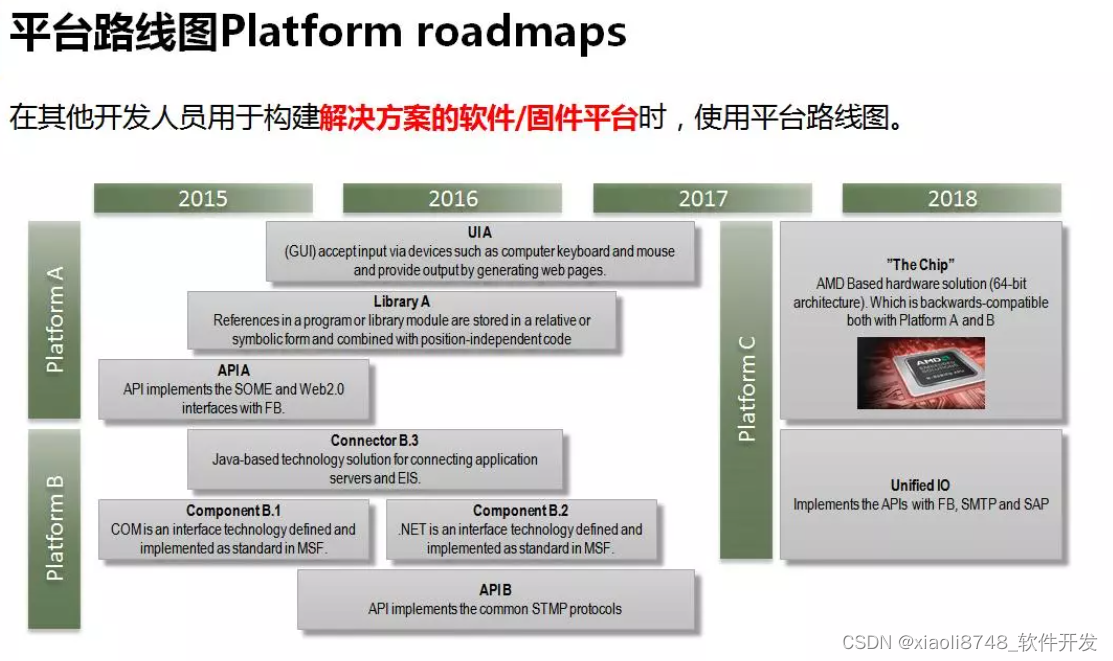
NPDP产品经理知识(产品创新管理)
复习文化,团队与领导力 产品创新管理: 如何树立愿景: 如何实现产品战略 计划 实施产品开发: 商业化,营销计划,推广活动 管理产品生命周期: 新式走向市场的流程:...
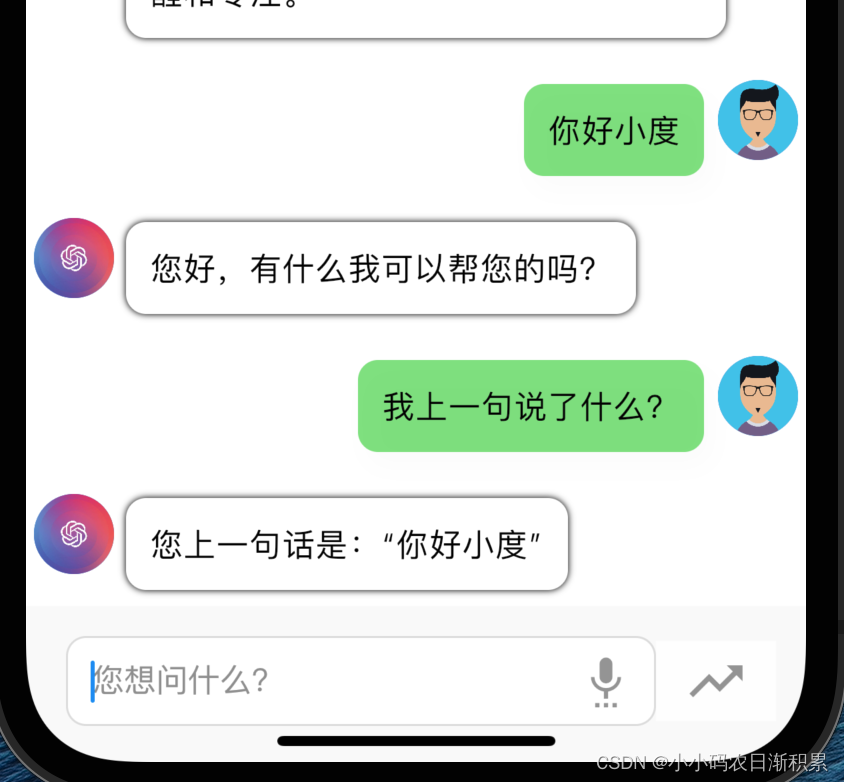
Flutter+SpringBoot实现ChatGPT流实输出
FlutterSpringBoot实现ChatGPT流式输出、上下文了连续对话 最终实现Flutter的流式输出上下文连续对话。 这里就是提供一个简单版的工具类和使用案例,此处页面仅参考。 服务端 这里直接封装提供工具类,修改自己的apiKey即可使用,支持连续…...
淘宝天猫粉丝福利购店铺优惠券去哪里找到领取网站?
淘宝天猫优惠券去哪里找到领取网站? 领取淘宝天猫粉丝福利购优惠券可通过百度搜索:草柴,进入草柴官方网站 或 手机应用商店搜索:草柴,下载安装草柴APP,就可以领取淘宝天猫优惠券; 草柴APP如何领…...

【考研复习】union有关的输出问题
文章目录 遇到的问题正确解答拓展参考文章 遇到的问题 首次遇到下面的代码时,感觉应该输出65,323。深入理解union的存储之后发现正确答案是:67,323. union {char c;int i; } u; int main(){u.c A;u.i 0x143;printf("%d,%d\n", u.c, u.i); …...
 Android 数据库Litepal)
Android学习之路(16) Android 数据库Litepal
一.LitePal的介绍 Litepal是Android郭霖大神的一个开源Android数据库的开源框架,它采用了对象关系映射(ORM)的模式,这是让我们非常好的理解的数据库,一个实体类对应我们数据库中的一个表。该库中还封装了许多的方法&a…...

Redis持久化(RDB/AOF)
"在哪里走散,你都会 找 到 我。" 认识持久化 我们在接触Mysql事务的时候,一定了解过Mysql事务的四个特性: "原子性(A)一致性(C)隔离性(I)持久性(D)" 而其中持久性其实与持久化是一回事,所谓持久与不持久&#x…...
小谈设计模式(15)—观察者模式
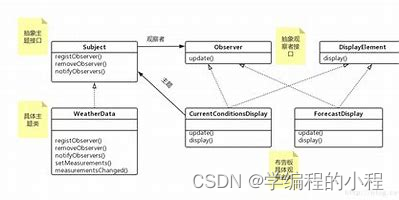
小谈设计模式(15)—观察者模式 专栏介绍专栏地址专栏介绍 观察者模式核心思想主要角色Subject(被观察者)ConcreteSubject(具体被观察者)Observer(观察者)ConcreteObserver࿰…...
)
简单工厂模式 创建型模式(非GoF经典设计模式)
简单工厂模式是属于创建型模式,也因为工厂中的方法一般设置为静态,又叫做静态工厂方法(Static Factory Method)模式,但不属于23种GOF设计模式之一。简单工厂模式是由一个工厂对象决定创建出哪一种产品类的实例。简单工…...
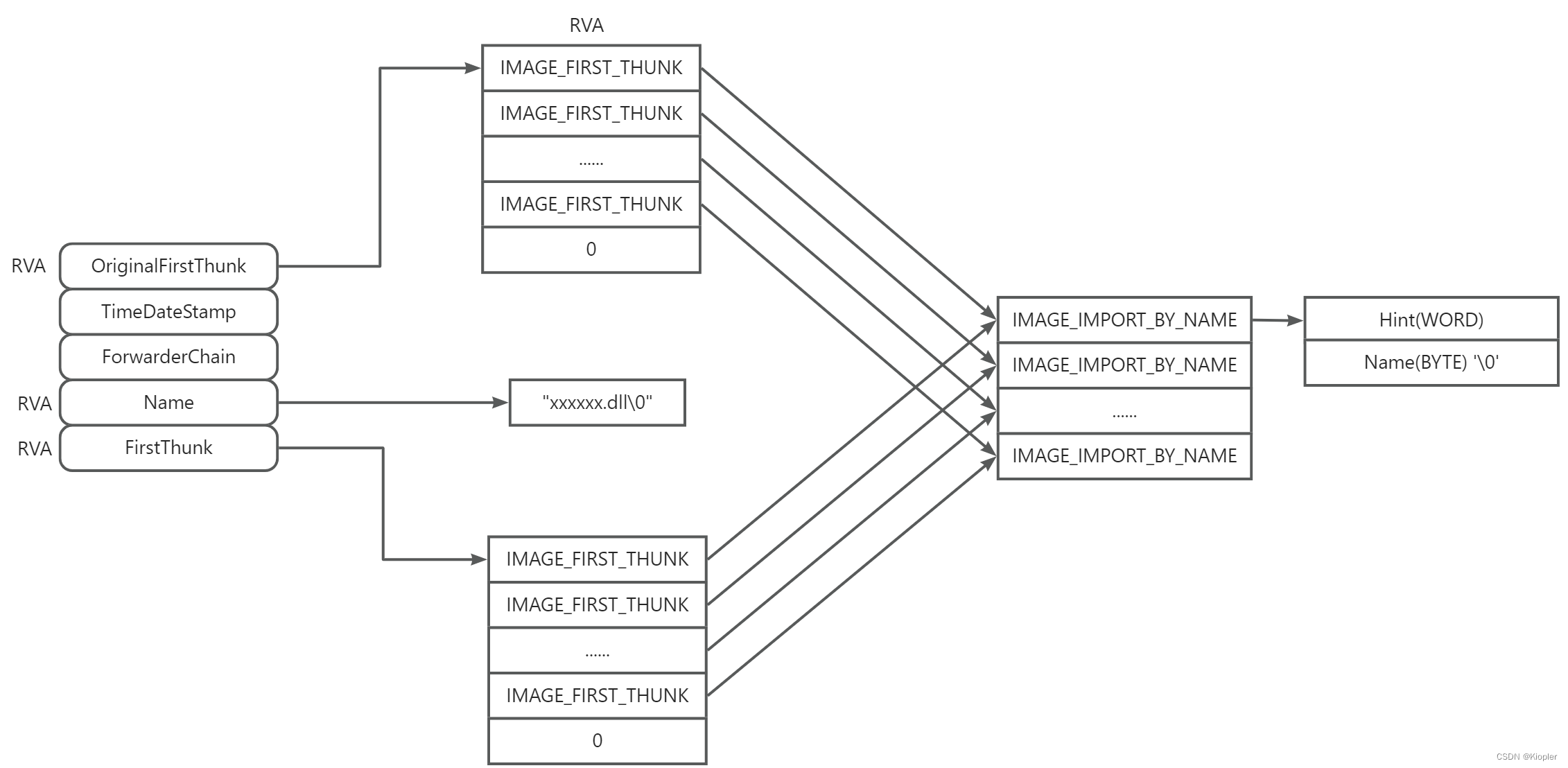
PE文件之导入表
1. 导入表 2. 显示导入表信息的例子 ; 作用: 将RVA地址转成FOA即文件偏移 ; 参数: _pFileHdr 指向读到内存中文件的基址指针 ; _dwRVA 目标RVA地址 ; 返回: 目标RVA转成文件偏移的值 RVA2FOA PROC USES esi edi edx, _pFileHdr:PTR BYTE, _dwRVA:DWORDmov esi, _pFil…...

二、码制及其转换
原码 根据我们所学可知,数字电路的逻辑电路是通过输出0和1来表示二进制数的,那么这个二进制数的正负又该怎么表示呢? 答案是在这个二进制数的最高位作为符号位来表示正负性,用0正数,用1表示负数,在这种表达…...
在pycharm中出现下载软件包失败的解决方法
一. 一般情况下我们会选择在设置中下载软件包,过程如下. 1. 直接点击左上角的文件, 再点击设置, 再点击项目, 在右边选择python解释器,点击号,输入要下载的软件包, 在下面的一系列的包中选择相对应的包,点击安装就可以了,有的时候我们下载的是最新的版本,如果要下载固定的版本…...
10.0 探索API调试事件原理
本章笔者将通过Windows平台下自带的调试API接口实现对特定进程的动态转存功能,首先简单介绍一下关于调试事件的相关信息,调试事件的建立需要依赖于DEBUG_EVENT这个特有的数据结构,该结构用于向调试器报告调试事件。当一个程序发生异常事件或者…...
文心一言 VS 讯飞星火 VS chatgpt (104)-- 算法导论10.1 2题
二、用go语言,说明如何在一个数组 A[1…n]中实现两个栈,使得当两个栈的元素个数之和不为 n 时,两者都不会发生上溢。要求 PUSH 和 POP 操作的运行时间为 O(1)。 文心一言: 在这个问题中,我们要在一个数组 A[1…n] 中…...
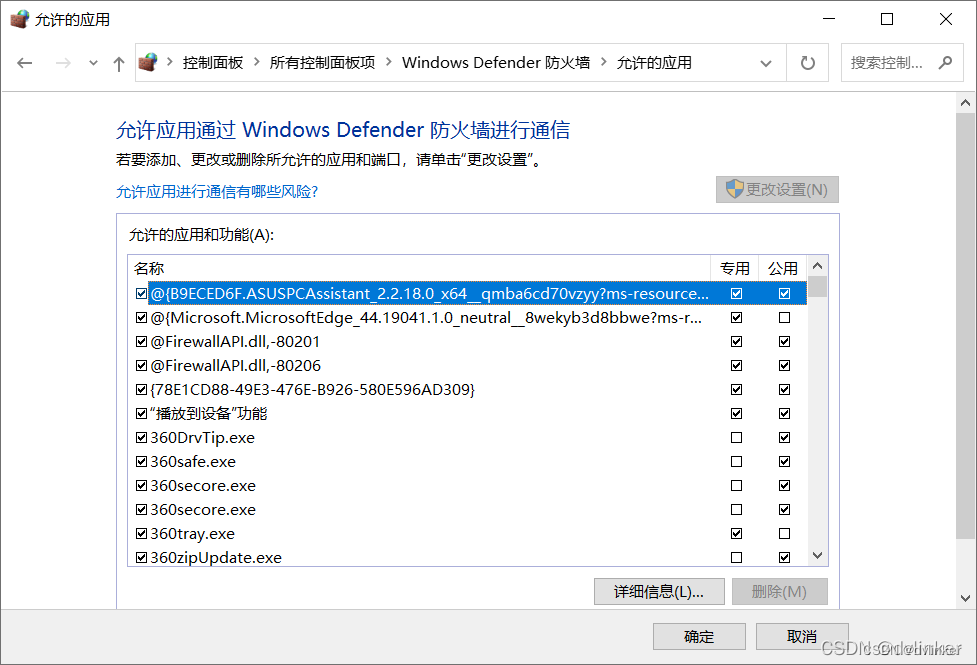
检测防火墙是否开启、判断程序是否加入防火墙白名单(附源码)
VC常用功能开发汇总(专栏文章列表,欢迎订阅,持续更新...)https://blog.csdn.net/chenlycly/article/details/124272585C软件异常排查从入门到精通系列教程(专栏文章列表,欢迎订阅,持续更新...&a…...
vtk 动画入门 1 代码
实现效果如图: #include <vtkAutoInit.h> //VTK_MODULE_INIT(vtkRenderingOpenGL2); //VTK_MODULE_INIT(vtkInteractionStyle); VTK_MODULE_INIT(vtkRenderingOpenGL2); VTK_MODULE_INIT(vtkInteractionStyle); //VTK_MODULE_INIT(vtkRenderingFreeType); #in…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...

CTF show 数学不及格
拿到题目先查一下壳,看一下信息 发现是一个ELF文件,64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断,第一个argc ! 5这个判断并没有起太大作用,主要是下面四个if判断 根据题目…...
