数据结构与算法之字典: Leetcode 76. 最小覆盖子串 (Typescript版)
最小覆盖子串
- https://leetcode.cn/problems/minimum-window-substring/description/
描述
- 给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。
- 注意:
- 对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量
- 如果 s 中存在这样的子串,我们保证它是唯一的答案
示例 1
输入:s = "ADOBECODEBANC", t = "ABC"
输出:"BANC"
解释:最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。
示例 2
输入:s = "a", t = "a"
输出:"a"
解释:整个字符串 s 是最小覆盖子串。
示例 3
输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中,因此没有符合条件的子字符串,返回空字符串。
提示
- m == s.length
- n == t.length
- 1 <= m, n <= 105
- s 和 t 由英文字母组成
进阶
- 你能设计一个在 o(m+n) 时间内解决此问题的算法吗?
算法实现
1 )双指针滑动窗口遍历
function minWindow(s: string, t: string): string {let l = 0;let r = 0;// 维护一个字典,表示子串需要的字符(键)以及长度(值)let m = new Map();// 遍历模板字符串t 用字典存储for(let c of t) {// 这样遍历,可以包含模板字符串t中存在重复的字符m.set(c, m.has(c) ? m.get(c) + 1 : 1);}// 哨兵变量 mSize 用于存储字典中字符的长度let mSize = m.size;// 用于存储输出结果let res = '';while(r < s.length) {let c = s[r];// 如果字典中有该值,那么字典中就不需要了if (m.has(c)) {// 比如s中遇到了A, 在m中有A, 那么在m中A就不再需要了// 如果模板字符串t中含有多个A, 那么此处减少一个Am.set(c, m.get(c) - 1);// 字典中相关字符已经用完if(!m.get(c)) {mSize--;}}// 此处监听mSize是否全部用完while(!mSize) {let newRes = s.substring(l, r + 1);if(!res || newRes.length < res.length) {res = newRes;}// 拿到左指针let c2 = s[l];if(m.has(c2)) {m.set(c2, m.get(c2) + 1);if(m.get(c2) === 1) {mSize ++;}}l++; // 左指针移动}r++; // 右指针移动}return res;
}
- 解题思路: 先找出所有的包含T的子串,找出长度最小那个子串,返回即可
- 用双指针维护一个滑动窗口,用于枚举所有子串
- 移动右指针,找到包含T的子串,移动左指针,尽量减少包含T的子串的长度
- 循环上述过程,找出包含T的最小子串
- 时间复杂度:O(m+n) = O(n)
- m是t的长度
- n是s的长度,两个while嵌套也是O(n), 就是移动两个指针
- 空间复杂度:O(m)
- m是t里不同字符的个数
- 这个题目难度级别为:困难
相关文章:
)
数据结构与算法之字典: Leetcode 76. 最小覆盖子串 (Typescript版)
最小覆盖子串 https://leetcode.cn/problems/minimum-window-substring/description/ 描述 给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。注意: 对于 t 中重…...

2023-10-03 VsCode诡异消失事件
VsCode诡异消失事件 前言一、排查问题二、原因分析三、其它可能不好的倾向总结 前言 今天打开电脑, 习惯性的打开VsCode, 收到错误消息, 该快捷方式所指向的项目Code.exe已经更改或移动, 因此该快捷方式无法正常工作. 是否删除该快捷方式. 一、排查问题 打开快捷方式指向的位…...

elementPlus表格组件el-table实现只能同时选择一行,全选按第一行处理
目录 需求背景: 具体实现: 模板代码: 函数处理代码: 代码讲解: 需求背景: 点击表格最左侧的复选框列,选中当前表格行,而且只允许选择一行,选中一行后,其…...

栈的应用场景(三)
最小栈 1.题目2.画图分析3.代码实现 1.题目 2.画图分析 3.代码实现 package Stack;import java.util.Stack; public class MinStack {private Stack <Integer> stack;private Stack <Integer> MinStack;public MinStack() {stack new Stack<>();MinStack …...

leetCode 45.跳跃游戏 II 贪心算法
45. 跳跃游戏 II - 力扣(LeetCode) 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 &…...
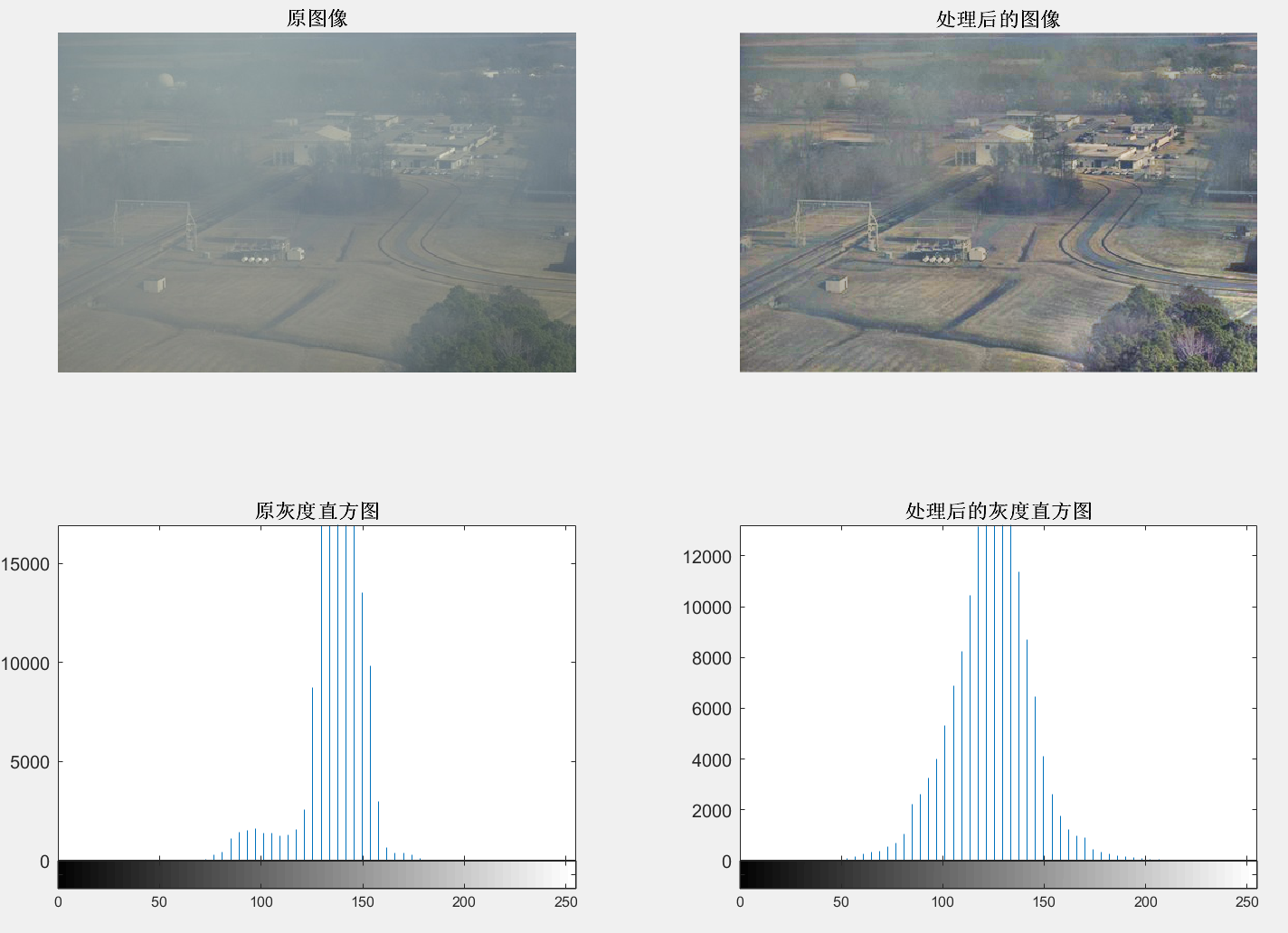
【MATLAB-基于直方图优化的图像去雾技术】
【MATLAB-基于直方图优化的图像去雾技术】 1 直方图均衡2 程序实现3 局部直方图处理 1 直方图均衡 直方图是图像的一种统计表达形式。对于一幅灰度图像来说,其灰度统计直方图可以反映该图像中不同灰度级出现的统计情况。一般而言,图像的视觉效果和其直方…...
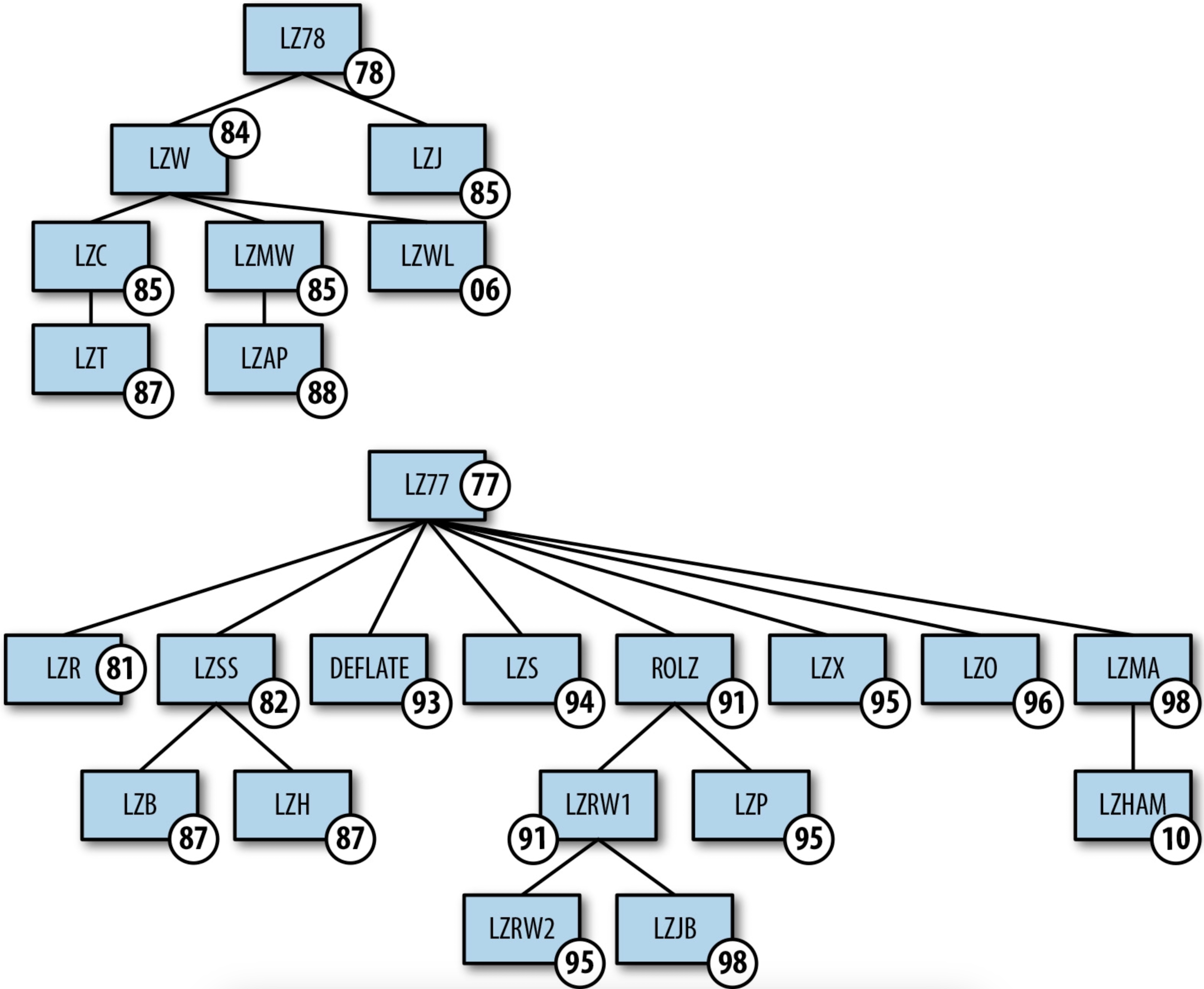
读书笔记|《数据压缩入门》—— 柯尔特·麦克安利斯 亚历克斯·海奇
前言:在接触文本隐写研究领域时了解到这本书。本书可算作《数据压缩》的入门书籍之一,这本书对熵编码、变长编码、统计编码、自适应统计编码、字典编码、上下文编码等常用编码方式的定义及来源进行介绍,对不同场景下不同格式的压缩数据有针对…...
)
Pandas进阶修炼120题-第五期(一些补充,101-120题)
目录 往期内容:第一期:Pandas基础(1-20题)第二期:Pandas数据处理(21-50题)第三期:Pandas金融数据处理(51-80题)第四期:当Pandas遇上NumPy…...
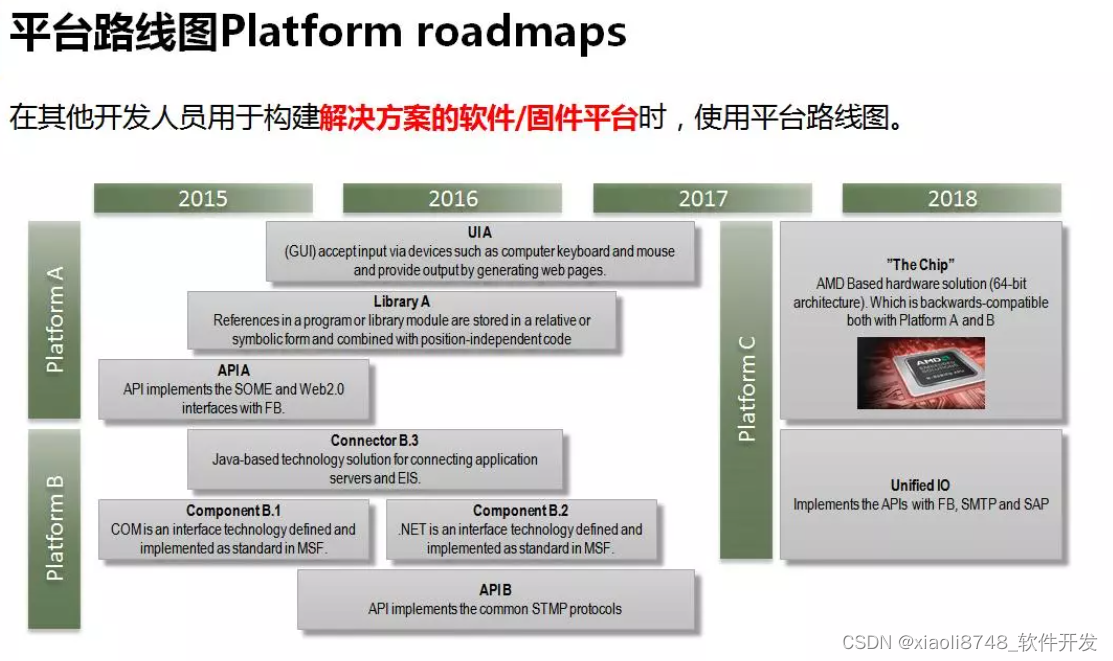
NPDP产品经理知识(产品创新管理)
复习文化,团队与领导力 产品创新管理: 如何树立愿景: 如何实现产品战略 计划 实施产品开发: 商业化,营销计划,推广活动 管理产品生命周期: 新式走向市场的流程:...
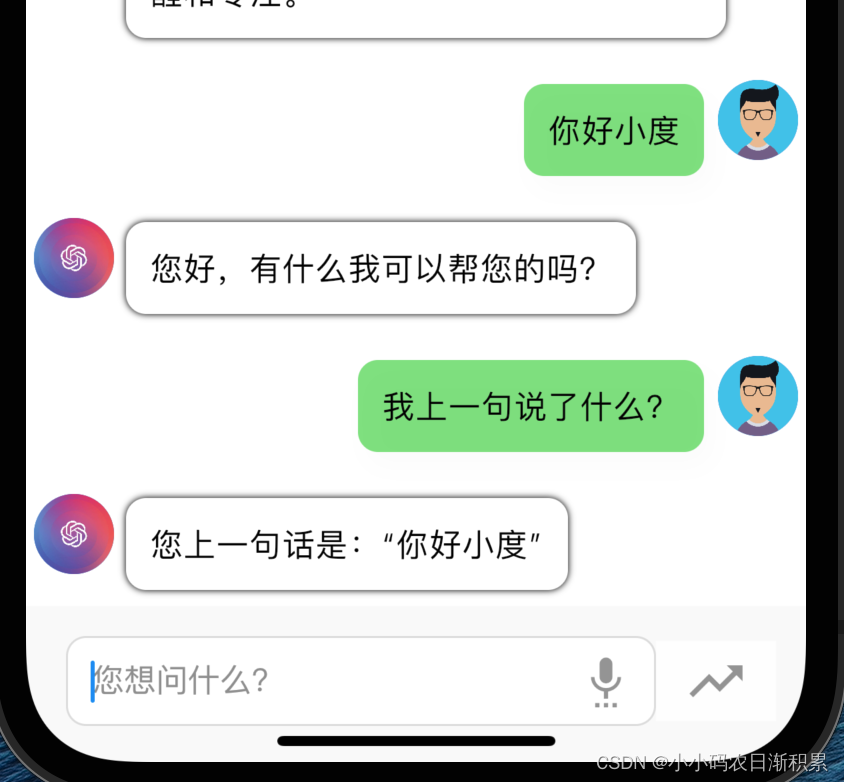
Flutter+SpringBoot实现ChatGPT流实输出
FlutterSpringBoot实现ChatGPT流式输出、上下文了连续对话 最终实现Flutter的流式输出上下文连续对话。 这里就是提供一个简单版的工具类和使用案例,此处页面仅参考。 服务端 这里直接封装提供工具类,修改自己的apiKey即可使用,支持连续…...
淘宝天猫粉丝福利购店铺优惠券去哪里找到领取网站?
淘宝天猫优惠券去哪里找到领取网站? 领取淘宝天猫粉丝福利购优惠券可通过百度搜索:草柴,进入草柴官方网站 或 手机应用商店搜索:草柴,下载安装草柴APP,就可以领取淘宝天猫优惠券; 草柴APP如何领…...

【考研复习】union有关的输出问题
文章目录 遇到的问题正确解答拓展参考文章 遇到的问题 首次遇到下面的代码时,感觉应该输出65,323。深入理解union的存储之后发现正确答案是:67,323. union {char c;int i; } u; int main(){u.c A;u.i 0x143;printf("%d,%d\n", u.c, u.i); …...
 Android 数据库Litepal)
Android学习之路(16) Android 数据库Litepal
一.LitePal的介绍 Litepal是Android郭霖大神的一个开源Android数据库的开源框架,它采用了对象关系映射(ORM)的模式,这是让我们非常好的理解的数据库,一个实体类对应我们数据库中的一个表。该库中还封装了许多的方法&a…...

Redis持久化(RDB/AOF)
"在哪里走散,你都会 找 到 我。" 认识持久化 我们在接触Mysql事务的时候,一定了解过Mysql事务的四个特性: "原子性(A)一致性(C)隔离性(I)持久性(D)" 而其中持久性其实与持久化是一回事,所谓持久与不持久&#x…...
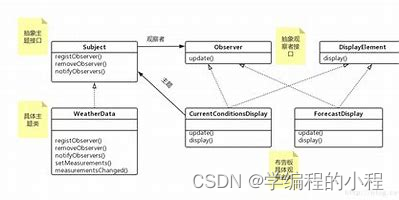
小谈设计模式(15)—观察者模式
小谈设计模式(15)—观察者模式 专栏介绍专栏地址专栏介绍 观察者模式核心思想主要角色Subject(被观察者)ConcreteSubject(具体被观察者)Observer(观察者)ConcreteObserver࿰…...
)
简单工厂模式 创建型模式(非GoF经典设计模式)
简单工厂模式是属于创建型模式,也因为工厂中的方法一般设置为静态,又叫做静态工厂方法(Static Factory Method)模式,但不属于23种GOF设计模式之一。简单工厂模式是由一个工厂对象决定创建出哪一种产品类的实例。简单工…...
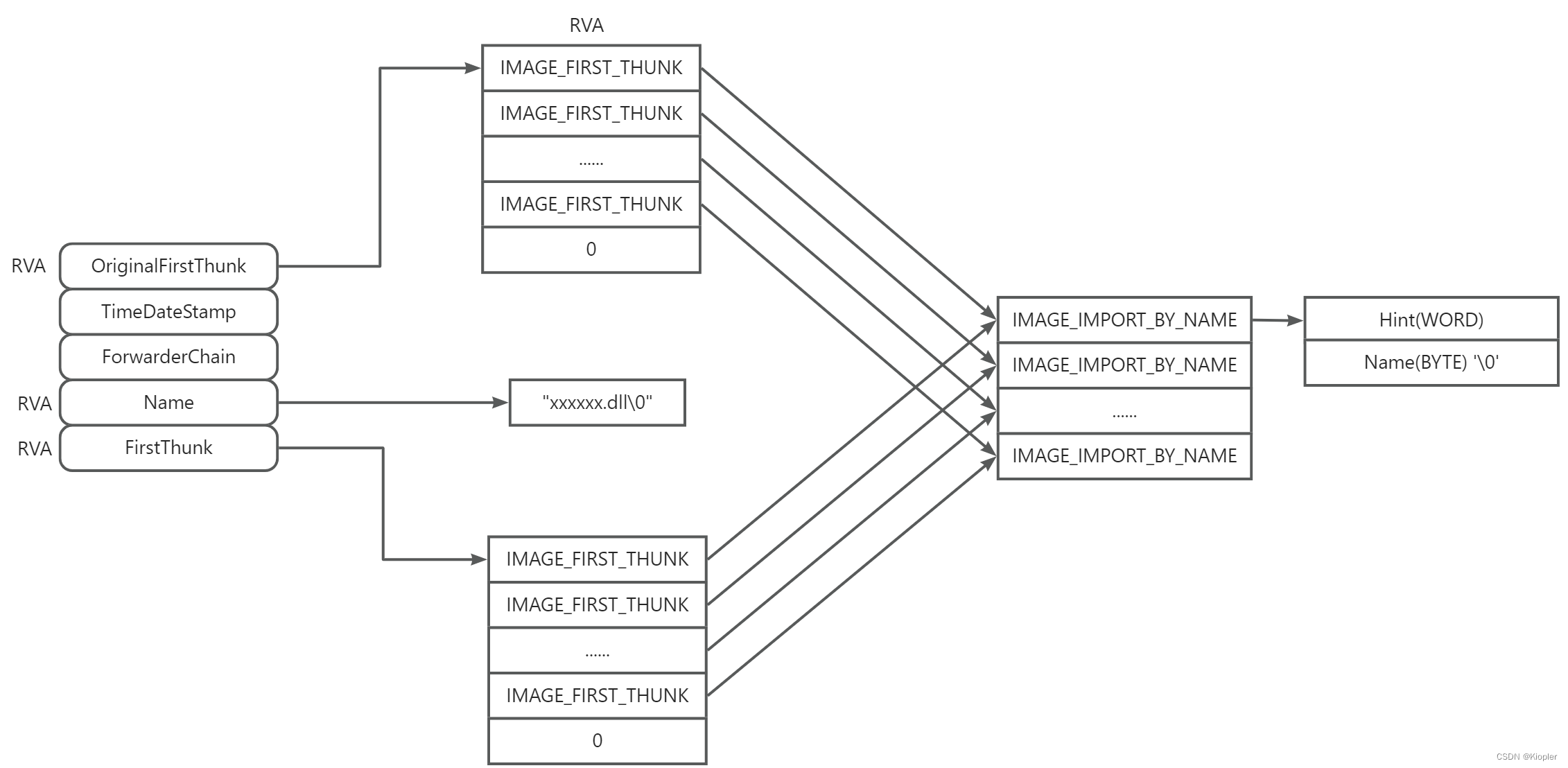
PE文件之导入表
1. 导入表 2. 显示导入表信息的例子 ; 作用: 将RVA地址转成FOA即文件偏移 ; 参数: _pFileHdr 指向读到内存中文件的基址指针 ; _dwRVA 目标RVA地址 ; 返回: 目标RVA转成文件偏移的值 RVA2FOA PROC USES esi edi edx, _pFileHdr:PTR BYTE, _dwRVA:DWORDmov esi, _pFil…...

二、码制及其转换
原码 根据我们所学可知,数字电路的逻辑电路是通过输出0和1来表示二进制数的,那么这个二进制数的正负又该怎么表示呢? 答案是在这个二进制数的最高位作为符号位来表示正负性,用0正数,用1表示负数,在这种表达…...
在pycharm中出现下载软件包失败的解决方法
一. 一般情况下我们会选择在设置中下载软件包,过程如下. 1. 直接点击左上角的文件, 再点击设置, 再点击项目, 在右边选择python解释器,点击号,输入要下载的软件包, 在下面的一系列的包中选择相对应的包,点击安装就可以了,有的时候我们下载的是最新的版本,如果要下载固定的版本…...
10.0 探索API调试事件原理
本章笔者将通过Windows平台下自带的调试API接口实现对特定进程的动态转存功能,首先简单介绍一下关于调试事件的相关信息,调试事件的建立需要依赖于DEBUG_EVENT这个特有的数据结构,该结构用于向调试器报告调试事件。当一个程序发生异常事件或者…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
