利用norm.ppfnorm.interval分别计算正态置信区间[实例]
scipy.stats.norm.ppf用于计算正态分布的累积分布函数CDF的逆函数,也称为百分位点函数。它的作用是根据给定的概率值,计算对应的随机变量值。
scipy.stats.norm.interval:用于计算正态分布的置信区间,可指定均值和标准差。
scipy.stats.t.interval:用于计算t分布的置信区间,可选择使用不同的置信水平和自由度。
利用norm.ppf&norm.interval分别计算正态置信区间:
import scipy.stats as stats
import numpy as np
# 指定概率值(例如,95% 置信水平对应的概率)
alpha = 0.05# 指定样本数据和样本大小
# data = [32, 34, 36, 35, 33, 31, 32, 33, 30, 34]
data = [34,56,39,71,84,92,44,67,98,49,55,73,50,62,75,44,88,53,61,25,36,66,77,35]
sample_size = len(data)# 执行D'Agostino's K-squared检验
stat, p_value = stats.normaltest(data)
# 输出结果
print("-------------------")
print("K-squared正态检验统计量:", stat)
print("K-squared正态检验P-value:", p_value)
# 判断是否符合正态分布的零假设
alpha = 0.05 # 显著性水平
if p_value < alpha:print("拒绝零假设,数据不符合正态分布。")
else:print("p_value>0.05无法拒绝零假设,数据符合正态分布。")
print("-------------------")# 计算样本均值和标准误差(标准差除以样本大小的平方根)
sample_mean = sum(data) / sample_size
sample_std = (sum([(x - sample_mean) ** 2 for x in data]) / (sample_size - 1)) ** 0.5
standard_error = sample_std / (sample_size ** 0.5)# 使用百分位点函数计算置信区间的上下限
confidence_interval_lower = stats.norm.ppf(alpha / 2, loc=sample_mean, scale=standard_error)
confidence_interval_upper = stats.norm.ppf(1 - alpha / 2, loc=sample_mean, scale=standard_error)# 输出置信区间的上下限
print("置信区间的下限:", confidence_interval_lower)
print("置信区间的上限:", confidence_interval_upper)print("-------------------")
# 计算正态分布的置信区间
confidence_interval = stats.norm.interval(1 - alpha, loc=sample_mean, scale=sample_std / np.sqrt(sample_size))
# 输出计算结果
print("norm.interval正态分布的置信区间:", confidence_interval)print("--------t分布结果是不是与上面的很接近?-----------")
# 计算t分布的置信区间
t_confidence_interval = stats.t.interval(1 - alpha, df=sample_size - 1, loc=sample_mean, scale=sample_std / np.sqrt(sample_size))
# 输出计算结果
print("t分布的置信区间:", t_confidence_interval)# -------------------
# K-squared正态检验统计量: 1.12645322945576
# K-squared正态检验P-value: 0.5693689625161796
# p_value>0.05无法拒绝零假设,数据符合正态分布。
# -------------------
# 置信区间的下限: 51.79799091398577
# 置信区间的上限: 67.70200908601423
# -------------------
# norm.interval正态分布的置信区间: (51.79799091398577, 67.70200908601423)
# -------------------
# t分布的置信区间: (51.356996738889045, 68.14300326111095)
# [Finished in 5.5s]附录多种方式正态检验:
import numpy as np
import pandas as pd
import scipy.stats as stats
import matplotlib.pyplot as plt# data = np.random.normal(loc=12, scale=2.5, size=340)
data = [34,56,39,71,84,92,44,67,98,49,55,73,50,62,75,44,88,53,61,25,36,66,77,35]
df = pd.DataFrame({'Data': data})# 描述性统计分析
mean = df['Data'].mean()
std_dev = df['Data'].std()
skewness = df['Data'].skew()
kurtosis = df['Data'].kurtosis()print("均值:", mean)
print("标准差:", std_dev)
print("偏度:", skewness)
print("峰度:", kurtosis)# 创建一个2x1的子图布局
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(6, 6))
# 可视化 - 正态概率图(Q-Q图)
stats.probplot(data, plot=ax1, dist='norm', fit=True, rvalue=True) #ax1作为绘图的位置
ax1.set_title("Q-Q Plot")# 可视化 - 直方图
ax2.hist(data, bins=6, rwidth=0.8, density=True) # bins个柱状图,宽度是rwidth(0~1),=1没有缝隙
ax2.set_title("Histogram with Kernel Density Estimate")# 调整子图之间的间距
plt.tight_layout()
# 显示图形
plt.show()# 正态性检验 - Shapiro-Wilk检验
stat, p = stats.shapiro(data)
print("Shapiro-Wilk检验统计量:", stat)
print("Shapiro-Wilk检验p值:", p)# Anderson-Darling检验
result = stats.anderson(df['Data'], dist='norm')
print("Anderson-Darling检验统计量:", result.statistic)
print("Anderson-Darling检验临界值:", result.critical_values)# 执行单样本K-S检验,假设数据服从正态分布
statistic, p_value = stats.kstest(data, 'norm')
print("K-S检验统计量:", statistic)
print("K-S检验p值:", p_value)# 执行正态分布检验
k2, p_value = stats.normaltest(data)
print(f"normaltest正态分布检验的统计量 (K^2): {k2}")
print(f"normaltest检验p值: {p_value}")
相关文章:

利用norm.ppfnorm.interval分别计算正态置信区间[实例]
scipy.stats.norm.ppf用于计算正态分布的累积分布函数CDF的逆函数,也称为百分位点函数。它的作用是根据给定的概率值,计算对应的随机变量值。scipy.stats.norm.interval:用于计算正态分布的置信区间,可指定均值和标准差。scipy.st…...

计算机网络各层设备
计算机网络通常被分为七层,每一层都有对应的设备。以下是各层设备的简要介绍: 物理层(Physical Layer):负责传输二进制数据位流的物理媒体和设备,例如网线、光纤、中继器、集线器等。 数据链路层…...

java this用法
在Java中,this是一个关键字,表示当前对象。它可以用来引用当前对象的实例变量、实例方法或者调用当前对象的构造方法。在本文中,我们将深入探讨Java中this关键字的用法。 1. 引用当前对象的实例变量 在Java中,this关键字可以用来…...

【AI视野·今日NLP 自然语言处理论文速览 第四十六期】Tue, 3 Oct 2023
AI视野今日CS.NLP 自然语言处理论文速览 Tue, 3 Oct 2023 (showing first 100 of 110 entries) Totally 100 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers Its MBR All the Way Down: Modern Generation Techniques Through the …...

Unity ddx与ddy
有关Unity的dx与dy的概念 引用的文章 1link 2link 3link 4link 有关概念 我们知道在光栅化的时刻,GPUs会在同一时刻并行运行很多Fragment Shader,但是并不是一个pixel一个pixel去执行的,而是将其组织在2x2的一组pixels分块中,…...

bootstrap.xml 和applicaiton.properties和applicaiton.yml的区别和联系
当谈到Spring Boot应用程序的配置时,有三个关键文件经常被提到:bootstrap.xml、application.properties和application.yml。这些文件在应用程序的不同阶段起着不同的作用,并在配置应用程序属性时有一些区别和联系。本文将探讨这些文件的作用、…...
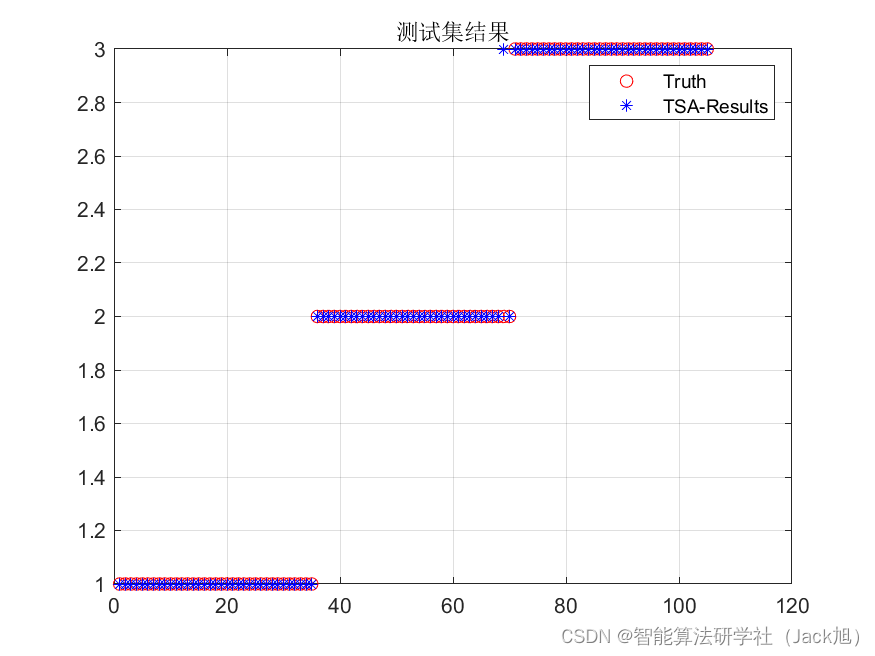
基于被囊群优化的BP神经网络(分类应用) - 附代码
基于被囊群优化的BP神经网络(分类应用) - 附代码 文章目录 基于被囊群优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.被囊群优化BP神经网络3.1 BP神经网络参数设置3.2 被囊群算法应用 4.测试结果&#x…...
我的第一个react.js 的router工程
react.js 开发的时候,都是针对一个页面的,多个页面就要用Router了,本文介绍我在vscode 下的第一个router 工程。 我在学习react.js 前端开发,学到router 路由的时候有点犯难了。经过1-2天的努力,终于完成了第一个工程…...

XXPermissions权限请求框架
官网 项目地址:Github博文地址:一句代码搞定权限请求,从未如此简单 框架亮点 一马当先:首款适配 Android 13 的权限请求框架简洁易用:采用链式调用的方式,使用只需一句代码体积感人:功能在同类…...

远程代码执行渗透测试—Server2128
远程代码执行渗透测试 任务环境说明: √ 服务器场景:Server2128(开放链接) √服务器场景操作系统:Windows √服务器用户名:Administrator密码:pssw0rd 1.找出靶机桌面上文件夹1中的文件RCEBac…...

阿里云关系型数据库有哪些?RDS云数据库汇总
阿里云RDS关系型数据库大全,关系型数据库包括MySQL版、PolarDB、PostgreSQL、SQL Server和MariaDB等,NoSQL数据库如Redis、Tair、Lindorm和MongoDB,阿里云百科分享阿里云RDS关系型数据库大全: 目录 阿里云RDS关系型数据库大全 …...

Linux--socket编程--服务端代码
查看struct sockaddr_in包含的东西: 在/user/include下搜索:grep "struct sockaddr_in { " * -nir r : 递归 i : 不区分大小写 n : 显示行号 socket编程–服务端代码 /* 1、调用 socket 创建套接字 2、调用 bind 添加地址 3、lis…...
安装Vue脚手架图文详解教程
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl 预备工作 在安装Vue脚手架之前,请确保您已经正确安装了npm;假若还尚未安装npm,请你参考 Node.js安装教程图文详解。 安装Vue脚手架 请…...
宠物医院必备,介绍一款宠物疫苗接种管理软件
在当今社会,养宠物已经成为越来越多人的生活方式,宠物疫苗接种已是宠物医院的重要工作,但是目前绝大多数的宠物医院对疫苗接种的管理,还是采取人工登记方式,不仅效率低下,而且无法做到疫苗接种到期自动提醒…...
哈哈,我保研985了,之后会出一期保研经验分享
哈哈,我保研了,之后会出一期保研经验分享 个人背景 学校:河南某四非,计算机科学与技术专业英语成绩:四级439,六级438(夏令营无六级)科研经历:一个软著、国家级大创&…...

C++ 程序员入门之路——旅程的起点与挑战
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

C/C++ 数组面试算法题
1.将一个数组逆序输出 https://blog.csdn.net/qq_45385706/article/details/110739961 1 #include<stdio.h>2 3 #define N 94 5 int main()6 {7 int a[N] {1,2,3,4,5,6,7,8,9};8 for(int i 0;i<N/2;i)9 { 10 int temp a[i]; 11 a[i]…...
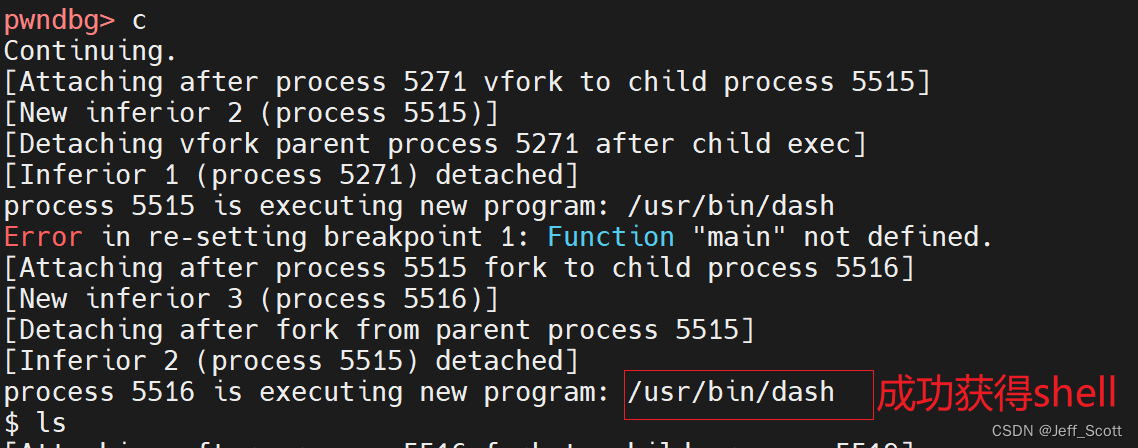
【pwn入门】用gdb实现第1个pwn
声明 本文是B站你想有多PWN学习的笔记,包含一些视频外的扩展知识。 有问题的源码 #include <stdio.h> #include <stdlib.h> #include <unistd.h> char sh[]"/bin/sh"; int func(char *cmd){system(cmd);return 0; }int main(){char …...

用pyinstaller打包LGBM模型为ELF/EXE可执行文件
1. 引入 写好的python代码和模型,如果需要做到离线部署、运行,就必须要将代码和模型打包为可独立运行的可执行文件。 使用pyinstaller就能做到这个,相同的代码,在windows上运行就能打包为exe,在linux上运行就能打包为…...
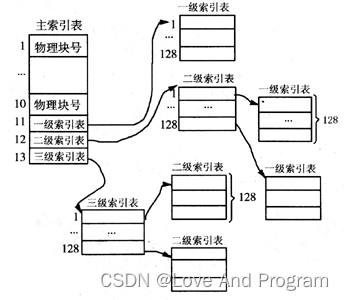
软考中级—— 操作系统知识
进程管理 操作系统概述 操作系统的作用:通过资源管理提高计算机系统的效率;改善人机界面向用户提供友好的工作环境。 操作系统的特征:并发性、共享性、虚拟性、不确定性。 操作系统的功能:进程管理、存储管理、文件管理、设备…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...
