利用t.ppft.interval分别计算T分布置信区间[实例]
scipy.stats.t.interval用于计算t分布的置信区间,即给定置信水平时,计算对应的置信区间的下限和上限。
scipy.stats.t.ppf用于计算t分布的百分位点,即给定百分位数(概率)时,该函数返回给定百分位数对应的t分布的值。//它的作用是根据给定的累积概率值,计算随机变量的值,使得该值以下的累积概率等于给定的概率。
利用t.ppf&t.interval分别计算T分布置信区间[实例]
import scipy.stats as stats
import numpy as np# 指定概率值(例如,95% 置信水平对应的概率)
alpha = 0.05# 指定样本数据
data = np.array([34,56,39,71,84,92,44,67,98,49,55,73,50,62,75,44,88,53,61,25,36,66,77,35])# 计算样本均值和标准误差
sample_mean = np.mean(data)
sample_std = np.std(data, ddof=1) # 使用ddof=1进行自由度校正
sample_size = len(data)
standard_error = sample_std / np.sqrt(sample_size)# 计算T分布的置信区间的上下限
t_critical = stats.t.ppf(1 - alpha / 2, df=sample_size - 1) # 自由度为样本大小减一
confidence_interval_lower = sample_mean - t_critical * standard_error
confidence_interval_upper = sample_mean + t_critical * standard_error# 输出T分布置信区间的上下限
print("T分布置信区间的下限:", confidence_interval_lower)
print("T分布置信区间的上限:", confidence_interval_upper)print("-------------------")
# 计算t分布的置信区间
t_confidence_interval = stats.t.interval(1 - alpha, df=sample_size - 1, loc=sample_mean, scale=sample_std / np.sqrt(sample_size))
# 输出计算结果
print("t分布的置信区间:", t_confidence_interval)# T分布置信区间的下限: 51.356996738889045
# T分布置信区间的上限: 68.14300326111095
# -------------------
# t分布的置信区间: (51.356996738889045, 68.14300326111095)
# [Finished in 5.1s]附录:多种方式进行T分布检验
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt# 创建一个样本数据,假设它符合T分布
np.random.seed(0)
sample_data = np.random.standard_t(df=5, size=100)# 绘制直方图
plt.hist(sample_data, bins=20, density=True, alpha=0.6, color='b', label='Histogram')# 绘制T分布的概率密度函数(PDF)曲线
x = np.linspace(min(sample_data), max(sample_data), 100)
pdf = stats.t.pdf(x, df=5)
plt.plot(x, pdf, 'r-', lw=2, label='T-Distribution PDF')# 添加图例和标签
plt.legend()
plt.title('Histogram and PDF of Sample Data')
plt.xlabel('Value')
plt.ylabel('Probability Density')# 显示图形
plt.show()# 绘制Q-Q图
stats.probplot(sample_data, dist="t", sparams=(5,), plot=plt)
plt.title('Q-Q Plot against T-Distribution')# 显示Q-Q图
plt.show()# 进行正态性检验(Shapiro-Wilk检验)
shapiro_test_statistic, shapiro_p_value = stats.shapiro(sample_data)
print("Shapiro-Wilk检验统计量:", shapiro_test_statistic)
print("Shapiro-Wilk检验p值:", shapiro_p_value)相关文章:

利用t.ppft.interval分别计算T分布置信区间[实例]
scipy.stats.t.interval用于计算t分布的置信区间,即给定置信水平时,计算对应的置信区间的下限和上限。 scipy.stats.t.ppf用于计算t分布的百分位点,即给定百分位数(概率)时,该函数返回给定百分位数对应的t…...
软件工程第三周
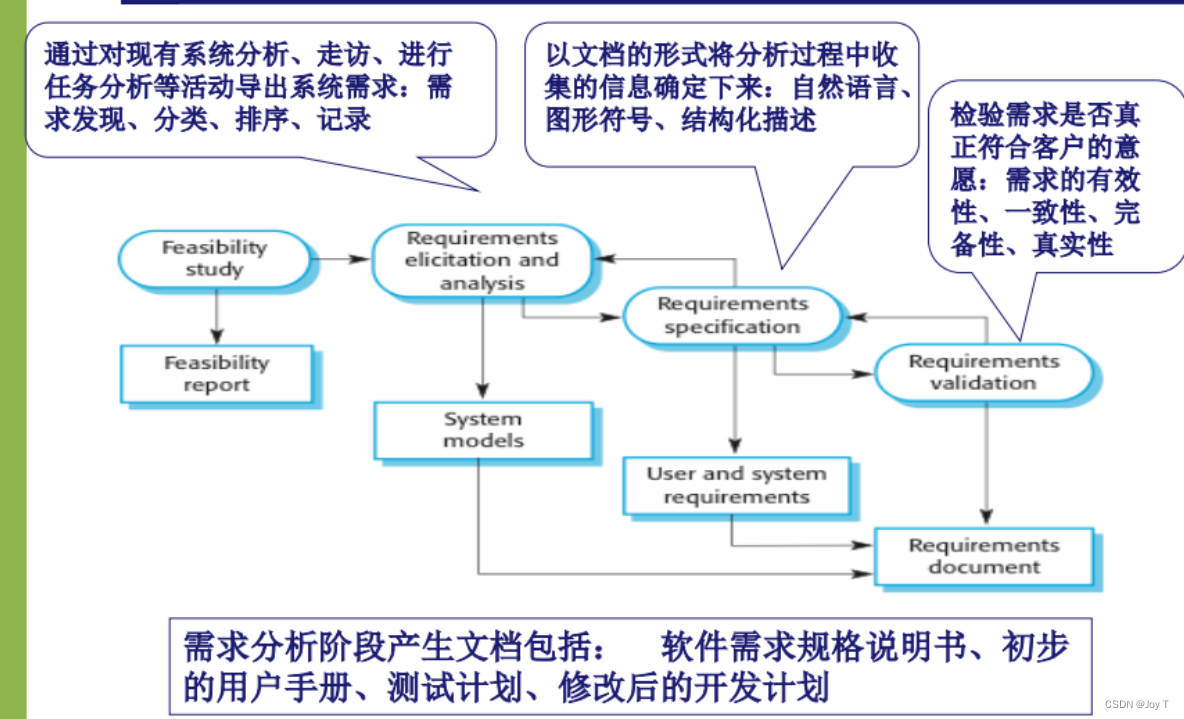
可行性研究 续 表达工作量的方式 LOC估算:Line of Code 估算公式S(Sopt4SmSpess)/6 FP:功能点 1. LOC (Line of Code) 估算 定义:LOC是指一个软件项目中的代码行数。 2. FP (Function Points) 估算 定义:FP是基于软件的功能性和…...
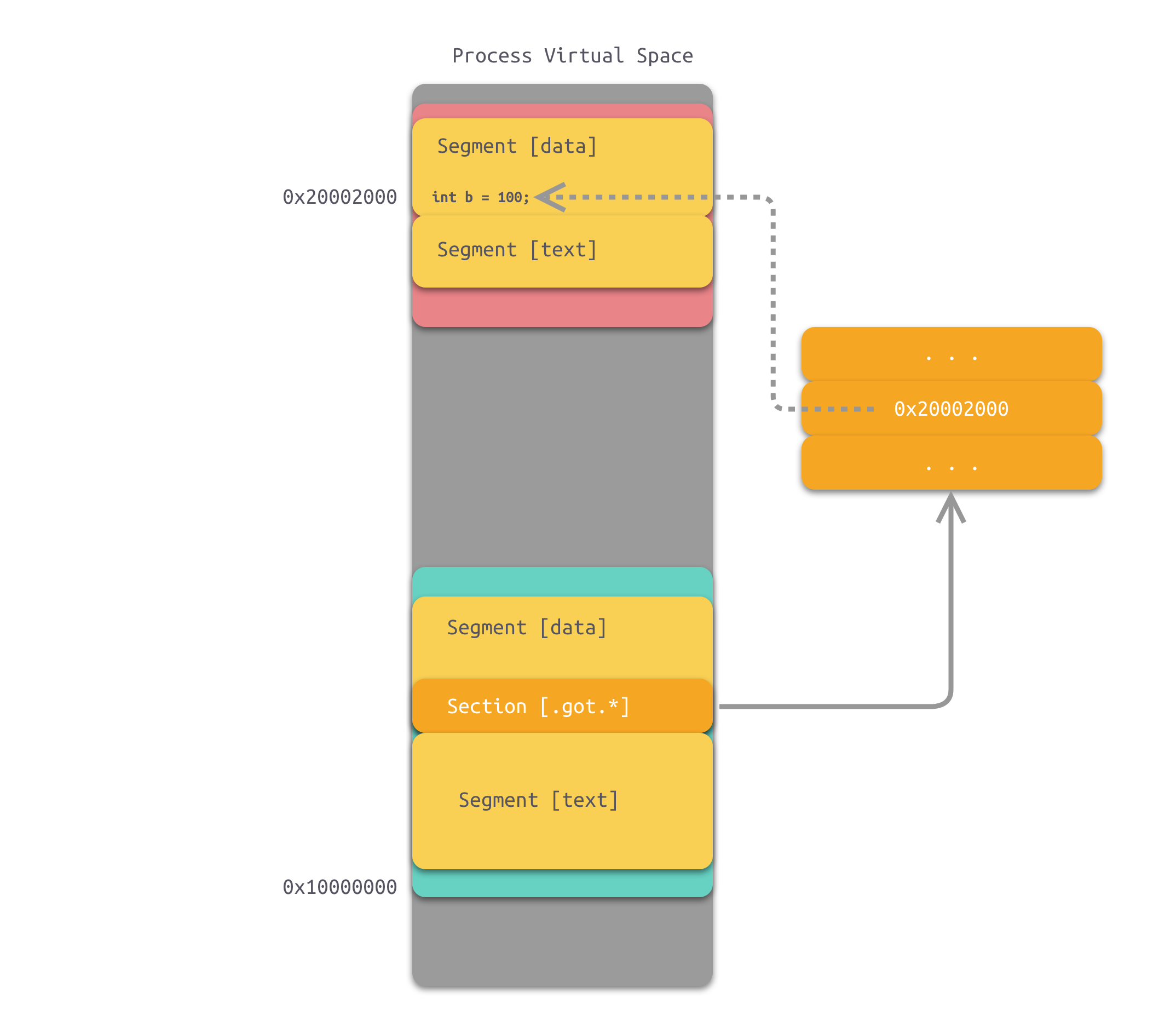
动态链接那些事
1、为什么要动态链接 1.1 空间浪费 对于静态链接来说,在程序运行之前,会将程序所需的所有模块编译、链接成一个可执行文件。这种情况下,如果 Program1 和 Program2 都需要用到 Lib.o 模块,那么,内存中和磁盘中实际上就…...

力扣:118. 杨辉三角(Python3)
题目: 给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。 在「杨辉三角」中,每个数是它左上方和右上方的数的和。 来源:力扣(LeetCode) 链接:力扣(LeetCode)官…...

QGIS文章二——DEM高程裁剪和3D地形图
经常看到别人基于高程文件制作出精美的3D地图,笔者按照互联网几种制作方式进行尝试后,写的DEM高程裁剪和3D地形图教程,或许其中有一些错误的,也请指出。 本文基于海南省的shp文件和海南省DEM高程文件,制作海口地区的3D…...

【kubernetes】kubernetes中的StatefulSet使用
TOC 1 为什么需要StatefulSet 常规的应用通常使用Deployment,如果需要在所有机器上部署则使用DaemonSet,但是有这样一类应用,它们在运行时需要存储一些数据,并且当Pod在其它节点上重建时也希望这些数据能够在重建后的Pod上获取&…...

创建文件夹
/storage/emulated/0/代码文件/ 没有就创建 文件名命名方法:编号. 库 时间戳 使用Python的os模块来检查目录是否存在,并在不存在时创建它。下面是一个示例代码,演示了如何检查指定路径下的目录是否存在,若不存在则创建…...

点击router-link时候会发生什么?
当你点击链接或按钮时,将会导航到 User 组件,就会显示相应的用户 ID。 这里说一下执行流程,当点击一个 router-link 时,Vue Router会执行以下流程: 1)点击事件触发: 当你点击 router-link 组件时…...

【Spring】@Bean方法中存在继承如何分析
文章目录 1. 提问:如果让您分析Spring MVC的原理,您如何开始分析呢2. 如何破局3. 资料参考 本文主要介绍:如何分析 Bean方法存在继承 或 Bean方法中存在调用子类方法。 1. 提问:如果让您分析Spring MVC的原理,您如何…...

【Vim 插件管理器】Vim-plug和Vim-vbundle的区别
- vundle是一款老款的插件管理工具 - vim-plug相对较新,特点是支持异步加载,相比vundle而言 Vim-plug 是一个自由、开源、速度非常快的、极简的 vim 插件管理器。它可以并行地安装或更新插件。你还可以回滚更新。它创建浅层克隆shallow clone最小化磁盘…...

电子计算机核心发展(继电器-真空管-晶体管)
目录 继电器 最大的机电计算机之一——哈弗Mark1号,IBM1944年 背景 组成 性能 核心——继电器 简介 缺点 速度 齿轮磨损 Bug的由来 真空管诞生 组成 控制开关电流 继电器对比 磨损 速度 缺点 影响 代表 第一个可编程计算机 第一个真正通用&am…...
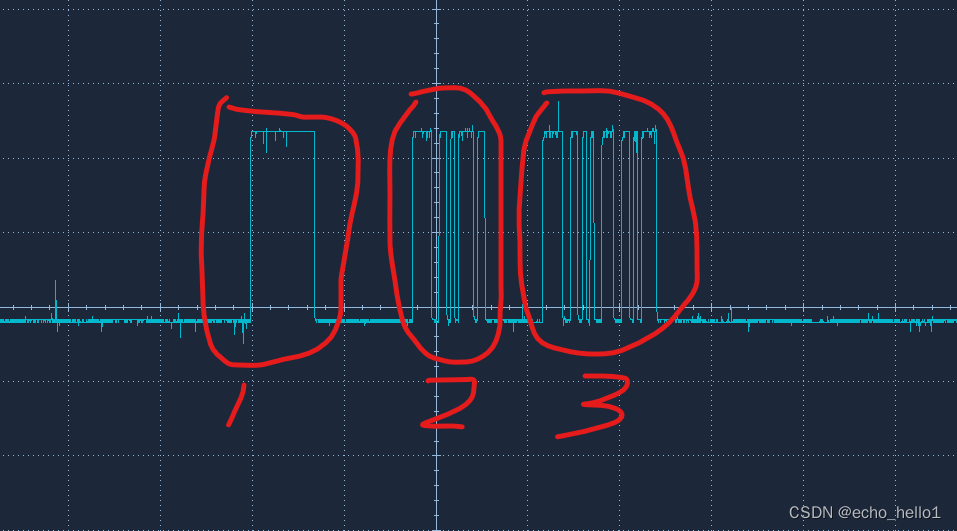
SDI-12协议与STM32 进行uart通信
场景是用stm32与一款温湿度传感器通信,不过是基于SDI-12协议,SDI-12时序和UART类似,故采用UART传输,原理图如下 其中DIR_OUT_SDI是一个IO引脚,控制UART_TX_SDI是否使能,U10是三态门IC,即拉低DIR…...

JS中的强制类型转换
JavaScript 中有多种强制类型转换的方式,可以将一个数据类型转换为另一种数据类型。这可以通过一些内置函数或操作符来实现。 显式类型转换(强制类型转换): 显式类型转换是通过特定的函数或操作符来明确指定要进行的类型转换。以下…...
WebSocket实战之四WSS配置
一、前言 上一篇文章WebSocket实战之三遇上PAC ,碰到的问题只能上安全的WebSocket(WSS)才能解决,配置证书还是挺麻烦的,主要是每年都需要重新更新证书,我配置过的证书最长有效期也只有两年,搞不…...
veImageX 演进之路:Web 图片加载提速50%
背景说明 火山引擎veImageX演进之路主要介绍了veImageX在字节内部从2012年随着字节成长过程中逐步演进的过程,演进中包括V1、V2、V3版本并最终面向行业输出;整个演进过程中包括服务端、客户端、网络库、业务场景与优化等多个角度介绍在图像处理压缩、省成…...
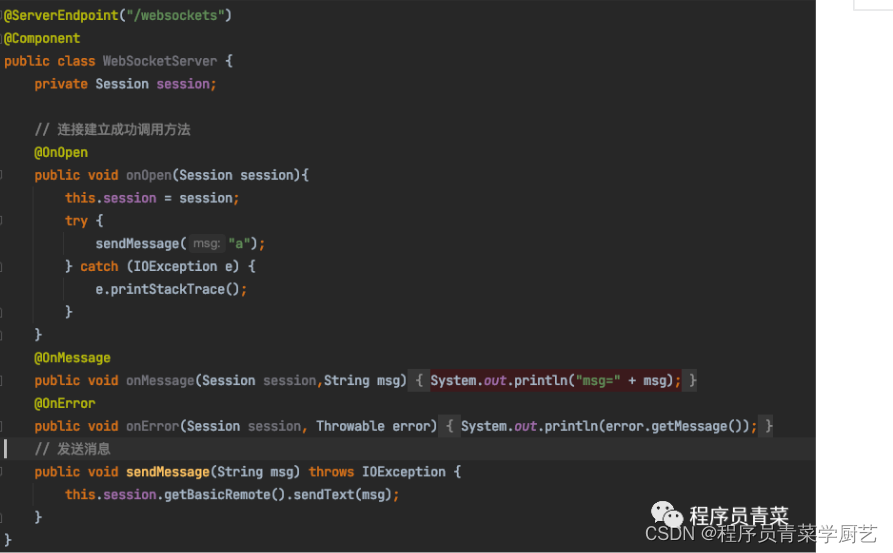
WebSocket实战之五JSR356
一、前言 前几篇WebSocket例子服务端我是用NodeJS实现,这一篇我们用Java来搭建一个WebSocket服务端,从2011年WebSocket协议RFC6455发布后,大多数浏览器都实现了WebSocket协议客户端的API,而对于服务端Java也定义了一个规范JSR356,即Java API for WebSoc…...

flask-sqlalchemy结合Blueprint遇到循环引入问题的解决方案
想要用flask_sqlalchemy结合Blueprint分模块写一下SQL的增删改查接口,结果发现有循环引入问题。 一开始,我在app.py中使用db SQLAlchemy(app)创建数据库对象;并且使用app.register_blueprint(db_bp, url_prefix/db)注册蓝图。 这使得我的依…...
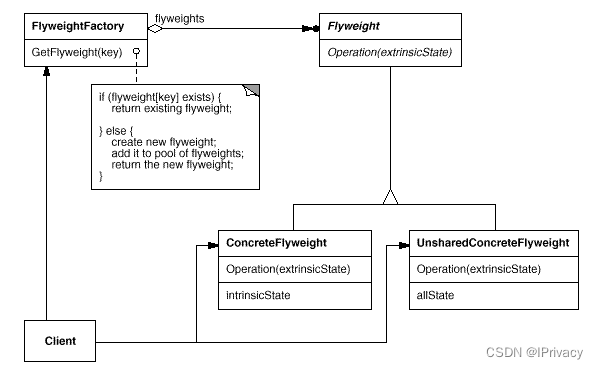
05_对象性能模式
对象性能模式 面向对象很好地解决了“抽象”的问题,但是必不可免地要付出定的代价。对于通常情况来讲,面向对象的成本大都可以忽略计。但是某些情况,面向对象所带来的成本必须谨慎处理。 典型模型: SingletonFlyweight Singleton 单件模式…...

快速选择排序
"你经过我每个灿烂时刻,我才真正学会如你般自由" 前些天有些无聊,想试试自己写的快排能否过leetcode上的排序算法题。结果是,不用截图可想而知,肯定是没过的,否则也不会有这篇文章的产出。 这份快排算法代码…...

国庆中秋特辑(六)大学生常见30道宝藏编程面试题
以下是 30 道大学生 Java 面试常见编程面试题和答案,包含完整代码: 什么是 Java 中的 main 方法? 答:main 方法是 Java 程序的入口点。它是一个特殊的方法,不需要被声明。当 Java 运行时系统执行一个 Java 程序时&…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...
