OpenGLES:绘制一个混色旋转的3D球体
效果展示
本篇博文会实现一个混色旋转的3D球体
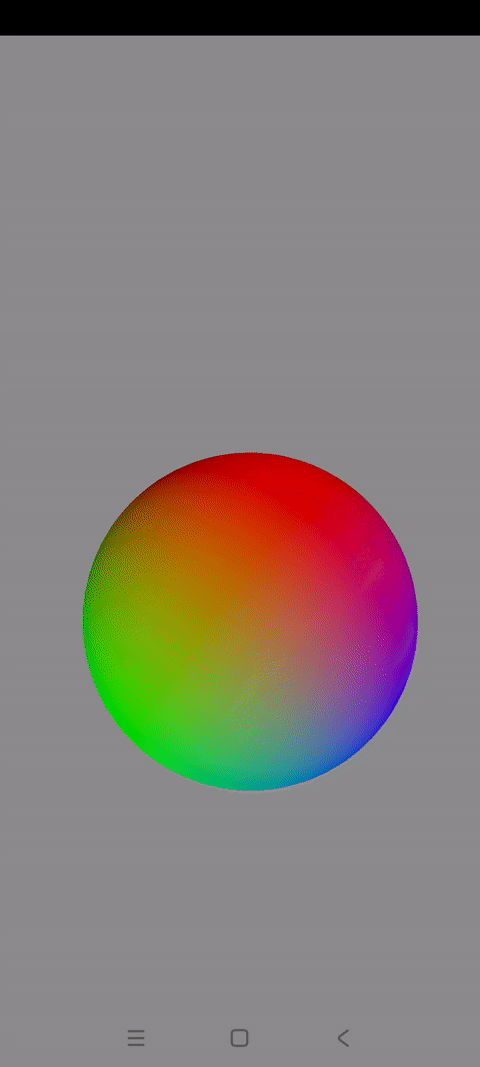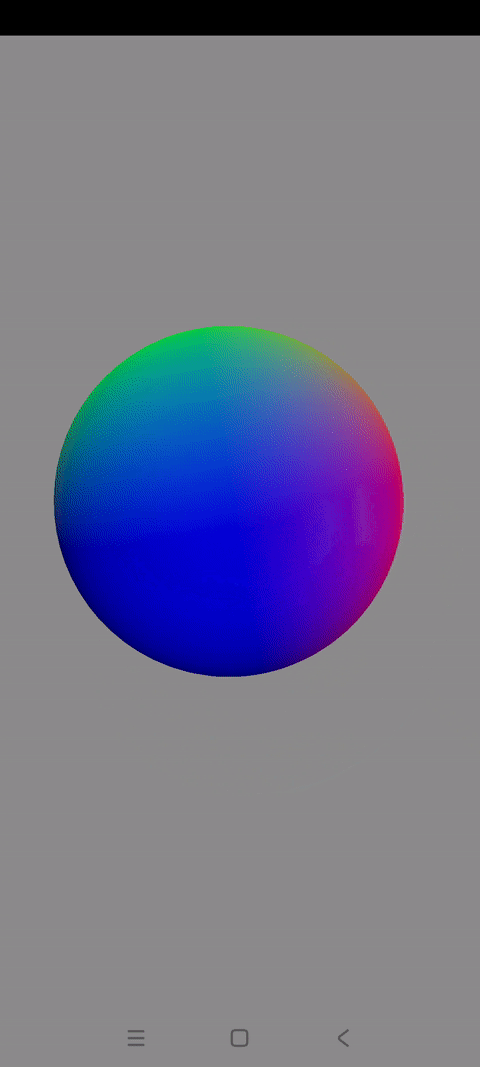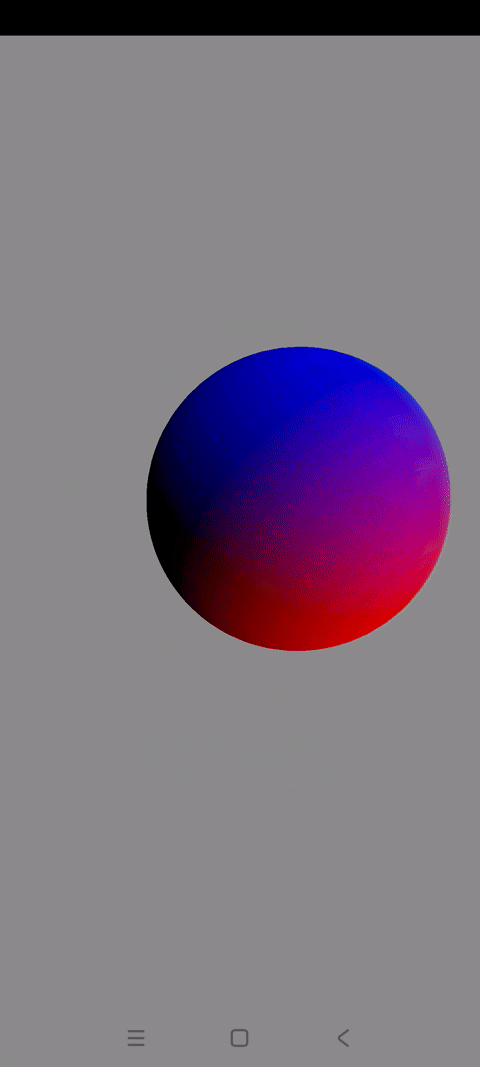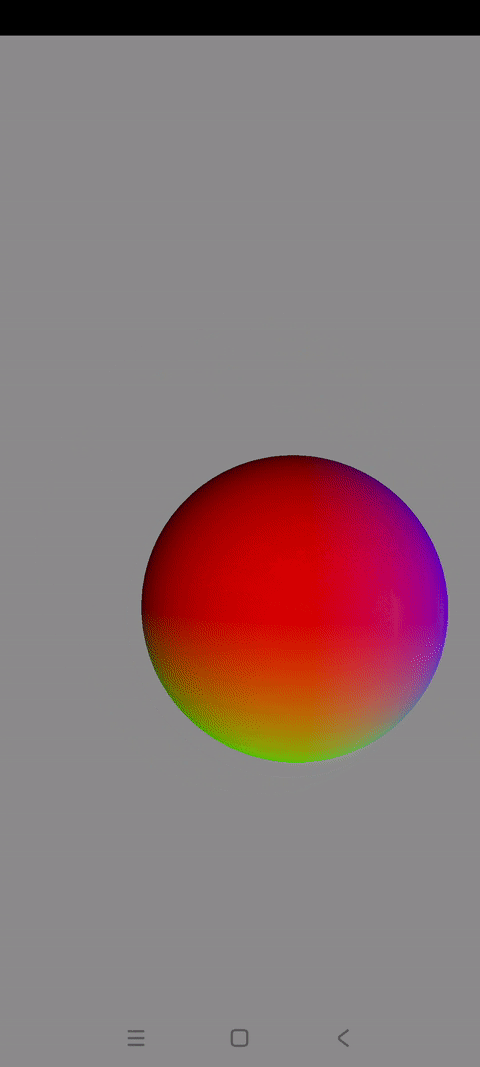
一.球体解析
前面几篇博文讲解了如何使用OpenGLES实现不同的3D图形
本篇博文讲解怎样实现3D世界的代表图形:一个混色旋转的3D球体
1.1 极限正多面体
如果有学习过我前几篇3D图形绘制的博文,就知道要想绘制一个3D图形,首先要做的第一步就是将要绘制的3D图形进行拆解,拆解成能够使用单位图元——三角形进行绘制的各种子图形
然而懂点微积分的都知道,球体本身就可以看作是一个被极限分解的正多面体
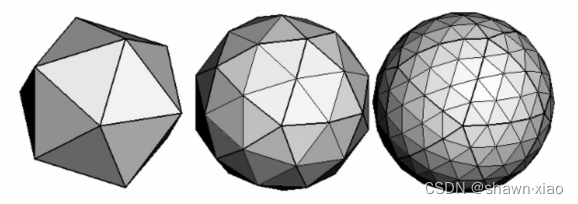
所以球面本身就可以使用三角形进行绘制,并不需要拆解成其他子图形
那么,现在要做的就是如何求解球体的顶点坐标。
1.2 求解球体顶点坐标
众所周知,地球上任何一个地方都能用经纬度进行标识
以此类推,先给球体设置一个经纬度
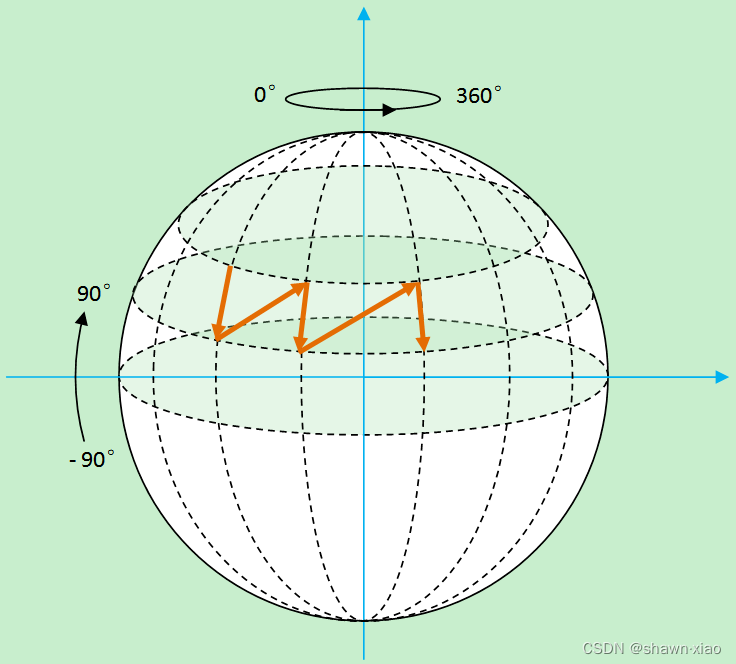
根据经纬度就将球体分解成四边形,再将四边形分解成三角形。
那么求解球体的坐标,就只需要求出四边形的坐标即可。

1.3 球体顶点坐标公式
根据上述讲解和图示,很容易就能得出球体顶点坐标公式:
- x0 = R * cos(a) * sin(b)
- y0 = R * sin(a))
- z0 = R * cos(a) * cos(b)
二.Render:变量定义
2.1 常规变量定义
还是常见的几个变量,跟其他3D图形的常规变量并无差别
//MVP矩阵
private float[] mMVPMatrix = new float[16];//着色器程序/渲染器
private int shaderProgram;//返回属性变量的位置
//MVP变换矩阵属性
private int mvpMatrixLoc;
//位置属性
private int aPositionLocation;
//颜色属性
private int aColorLocation;//surface宽高比
private float ratio;2.2 定义顶点坐标数组和缓冲
前文中已经讲解,对于球体,并不需要拆解出子图形,而且颜色混合我会在着色器代码中实现,并不会在Render代码中动态加载实现,因此只需要定义一个数组和缓冲,就是顶点坐标。
//球体顶点坐标数组
private float vertexData[];
//顶点缓冲
private FloatBuffer vertexBuffer;2.3 定义MVP矩阵
//MVP矩阵
private float[] mMVPMatrix = new float[16];三.Render:着色器、内存分配等
3.1 着色器创建、链接、使用
3.2 着色器属性获取、赋值
3.3 缓冲内存分配
这几个部分的代码实现2D图形绘制基本一致
可参考以前2D绘制的相关博文,里面都有详细的代码实现
不再重复展示代码
四.Render:动态创建顶点
创建顶点时需要传入半径:0.85f
createBallPositions(0.85f);球体渲染的关键函数:
createBallPositions(float r):
private void createBallPositions(float r) {// 存放顶点坐标的ArrayListArrayList<Float> alVertix = new ArrayList<Float>();// 将球进行单位切分的角度final int angleSpan = 5;// 纬度angleSpan度一份for (int wAngle = -90; wAngle < 90; wAngle = wAngle + angleSpan) {// 经度angleSpan度一份for (int jAngle = 0; jAngle <= 360; jAngle = jAngle + angleSpan) {// 纵向横向各到一个角度后计算对应的此点在球面上的坐标float x0 = (float) (r * Math.cos(Math.toRadians(wAngle)) * Math.sin(Math.toRadians(jAngle)));float y0 = (float) (r * Math.sin(Math.toRadians(wAngle)));float z0 = (float) (r * Math.cos(Math.toRadians(wAngle)) * Math.cos(Math.toRadians(jAngle)));float x1 = (float) (r * Math.cos(Math.toRadians(wAngle)) * Math.sin(Math.toRadians(jAngle + angleSpan)));float y1 = (float) (r * Math.sin(Math.toRadians(wAngle)));float z1 = (float) (r * Math.cos(Math.toRadians(wAngle)) * Math.cos(Math.toRadians(jAngle + angleSpan)));float x2 = (float) (r * Math.cos(Math.toRadians(wAngle + angleSpan)) * Math.sin(Math.toRadians(jAngle + angleSpan)));float y2 = (float) (r * Math.sin(Math.toRadians(wAngle + angleSpan)));float z2 = (float) (r * Math.cos(Math.toRadians(wAngle + angleSpan)) * Math.cos(Math.toRadians(jAngle + angleSpan)));float x3 = (float) (r * Math.cos(Math.toRadians(wAngle + angleSpan)) * Math.sin(Math.toRadians(jAngle)));float y3 = (float) (r * Math.sin(Math.toRadians(wAngle + angleSpan)));float z3 = (float) (r * Math.cos(Math.toRadians(wAngle + angleSpan)) * Math.cos(Math.toRadians(jAngle)));// 将计算出来的XYZ坐标加入存放顶点坐标的ArrayListalVertix.add(x1);alVertix.add(y1);alVertix.add(z1);alVertix.add(x0);alVertix.add(y0);alVertix.add(z0);alVertix.add(x2);alVertix.add(y2);alVertix.add(z2);alVertix.add(x3);alVertix.add(y3);alVertix.add(z3);/*2---------------3| / || / || / || / || / |1---------------0*/}}float f[] = new float[alVertix.size()];for (int i = 0; i < f.length; i++) {f[i] = alVertix.get(i);}vertexData = f;
}五.Render:绘制
5.1 MVP矩阵
//MVP矩阵赋值
mMVPMatrix = TransformUtils.getBallMVPMatrix(ratio);
//将变换矩阵传入顶点渲染器
glUniformMatrix4fv(mvpMatrixLoc, 1, false, mMVPMatrix, 0);
getBallMVPMatrix(float ratio)
依然采用的是视椎体透视投影:
public static float[] getBallMVPMatrix(float ratio) {float[] modelMatrix = getIdentityMatrix(16, 0); //模型变换矩阵float[] modelMatrix0 = getIdentityMatrix(16, 0); //模型变换矩阵float[] viewMatrix = getIdentityMatrix(16, 0); //观测变换矩阵/相机矩阵float[] projectionMatrix = getIdentityMatrix(16, 0); //投影变换矩阵mBallRotateAgree = (mBallRotateAgree + 1.0f) % 360;Matrix.setRotateM(modelMatrix, 0, mBallRotateAgree, 1, 0, 1);Matrix.translateM(modelMatrix0,0,0.0f,0.3f,0.3f);Matrix.multiplyMM(modelMatrix, 0, modelMatrix, 0, modelMatrix0, 0);Matrix.setLookAtM(viewMatrix, 0, 0, 0, 3, 0f, 0f, 0f, 0f, 1.0f, 0.0f);Matrix.frustumM(projectionMatrix, 0, -ratio, ratio, -1, 1, 1, 10);float[] tmpMatrix = new float[16];float[] mvpMatrix = new float[16];Matrix.multiplyMM(tmpMatrix, 0, viewMatrix, 0, modelMatrix, 0);Matrix.multiplyMM(mvpMatrix, 0, projectionMatrix, 0, tmpMatrix, 0);return mvpMatrix;
}
5.2 绘制球体
//准备顶点坐标内存
glVertexAttribPointer(aPositionLocation, 3, GL_FLOAT, false, 0, vertexBuffer);
//绘制
glDrawArrays(GL_TRIANGLE_STRIP, 0, vertexData.length / 3);六.着色器代码
(1).ball_vertex_shader.glsl
#version 300 eslayout (location = 0) in vec4 vPosition;
layout (location = 1) in vec4 aColor;uniform mat4 u_Matrix;out vec4 vColor;void main() {gl_Position = u_Matrix*vPosition;float x = vPosition.x;float y = vPosition.y;float z = vPosition.z;//效果较真实vColor = vec4(x, y, z, 0.0);
}
(2).ball_fragtment_shader.glsl
#version 300 es
#extension GL_OES_EGL_image_external_essl3 : require
precision mediump float;in vec4 vColor;out vec4 outColor;void main(){outColor = vColor;
}
八.结束语
混色旋转3D球体的绘制过程到此讲解结束了
最终实现出来的效果如同开头效果展示
相关文章:

OpenGLES:绘制一个混色旋转的3D球体
效果展示 本篇博文会实现一个混色旋转的3D球体 一.球体解析 前面几篇博文讲解了如何使用OpenGLES实现不同的3D图形 本篇博文讲解怎样实现3D世界的代表图形:一个混色旋转的3D球体 1.1 极限正多面体 如果有学习过我前几篇3D图形绘制的博文,就知道要想…...

Spring AOP 基于注解源码整理
导入配置类 EnableAspectJAutoProxy 注解导入 AspectJAutoProxyRegistrarImportBeanDefinitionRegistrar#registerBeanDefinitions向容器中加入AnnotationAwareAspectJAutoProxyCreatorAnnotationAwareAspectJAutoProxyCreator#initBeanFactory初始化ReflectiveAspectJAdvisor…...
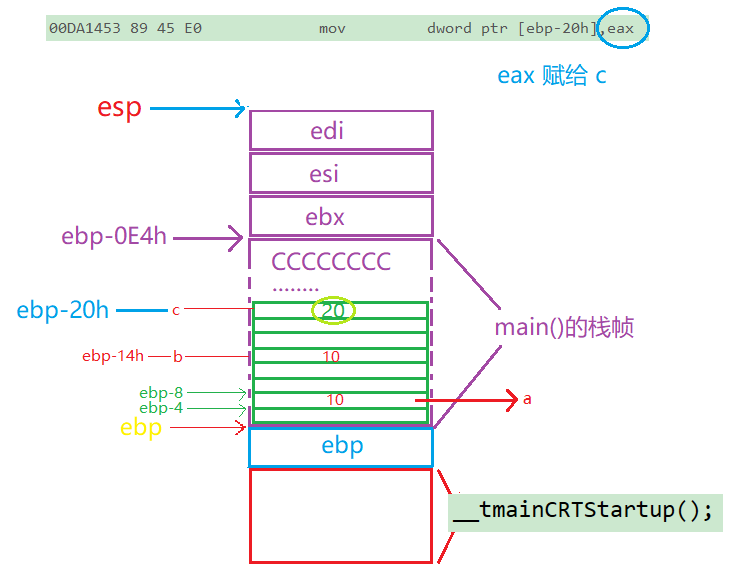
C语言 —— 函数栈帧的创建和销毁
在我们之前学习函数的时候,我们可能有很多困惑? 比如: 局部变量是怎么创建的?为什么局部变量的值是随机值?函数是怎么传参的?传参的顺序是怎样的?形参和实参是什么关系?函数调用是怎么做的?函数调用是结束后怎么返回的? 那么要解决这些问题, 我们就需要知道…...

Appleid苹果账号自动解锁改密(自动解锁二验改密码)
目前该项目能实现以下功能: 多用户使用,权限控制多账号管理账号分享页,支持设置密码、有效期、自定义HTML内容自动解锁与关闭二步验证自动/定时修改密码自动删除Apple ID中的设备代理池与Selenium集群,提高解锁成功率允许手动触发…...

Conflicting peer dependency: eslint@8.50.0
npm install 输出 npm ERR! code ERESOLVE npm ERR! ERESOLVE could not resolve npm ERR! npm ERR! While resolving: vue/eslint-config-standard6.1.0 npm ERR! Found: eslint-plugin-vue8.7.1 npm ERR! node_modules/eslint-plugin-vue npm ERR! dev eslint-plugin-vue…...

Vue3 defineProps使用
MyTag.vue <script setup> import { ref, nextTick, defineProps, defineEmits } from "vue"; const props defineProps({flag: Boolean,title: String, }); // 写成这样也可以 // const props defineProps(["flag", "title"]);const e…...
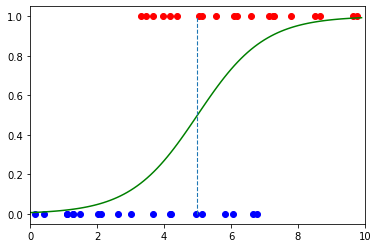
机器学习7:逻辑回归
一、说明 逻辑回归模型是处理分类问题的最常见机器学习模型之一。二项式逻辑回归只是逻辑回归模型的一种类型。它指的是两个变量的分类,其中概率用于确定二元结果,因此“二项式”中的“bi”。结果为真或假 — 0 或 1。 二项式逻辑回归的一个例子是预测人…...

生活小记-纸张尺寸
A系列纸张: A0:841 x 1189 毫米A1:594 x 841 毫米A2:420 x 594 毫米A3:297 x 420 毫米A4:210 x 297 毫米A5:148 x 210 毫米A6:105 x 148 毫米A7:74 x 105 毫米A8…...
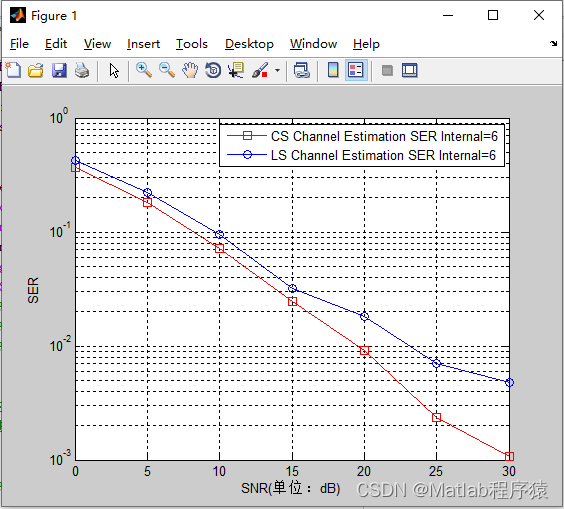
【MATLAB源码-第41期】基于压缩感知算法的OFDM系统信道估计和LS算法对比仿真。
操作环境: MATLAB 2013b 1、算法描述 压缩感知(Compressed Sensing, CS)是一种从稀疏或可压缩信号中重构完整信号的数学理论和技术。下面详细介绍压缩感知和它在OFDM信道估计中的应用。 1. 压缩感知基本概念 在传统采样理论中࿰…...

优思学院|六西格玛将烹饪和美味提升至极致
最近,我们曾提到一个美国男子如何利用六西格玛来控制糖尿病。这表明六西格玛逐渐被认为是一个不仅可以在工作场所之外使用,尤其不仅限于制造业的系统。 六西格玛的核心理念是改进过程的质量,从而改善最终结果。如果你做了晚餐或尝试了一道新…...

git stash
git stash 是 Git 中一个非常有用的命令,用于临时保存当前工作目录中的修改,以便你可以切换到其他分支或处理其他任务而不丢失你的修改。它的主要用途是: 保存未提交的修改:你可以使用 git stash 命令将未提交的修改(包…...

Flink Data Source
Flink Data Source 一、内置 Data Source Flink Data Source 用于定义 Flink 程序的数据来源,Flink 官方提供了多种数据获取方法,用于帮助开发者简单快速地构建输入流,具体如下: 1.1 基于文件构建 1. readTextFile(path):按照 TextInputFormat 格式读取文本文件,并将…...
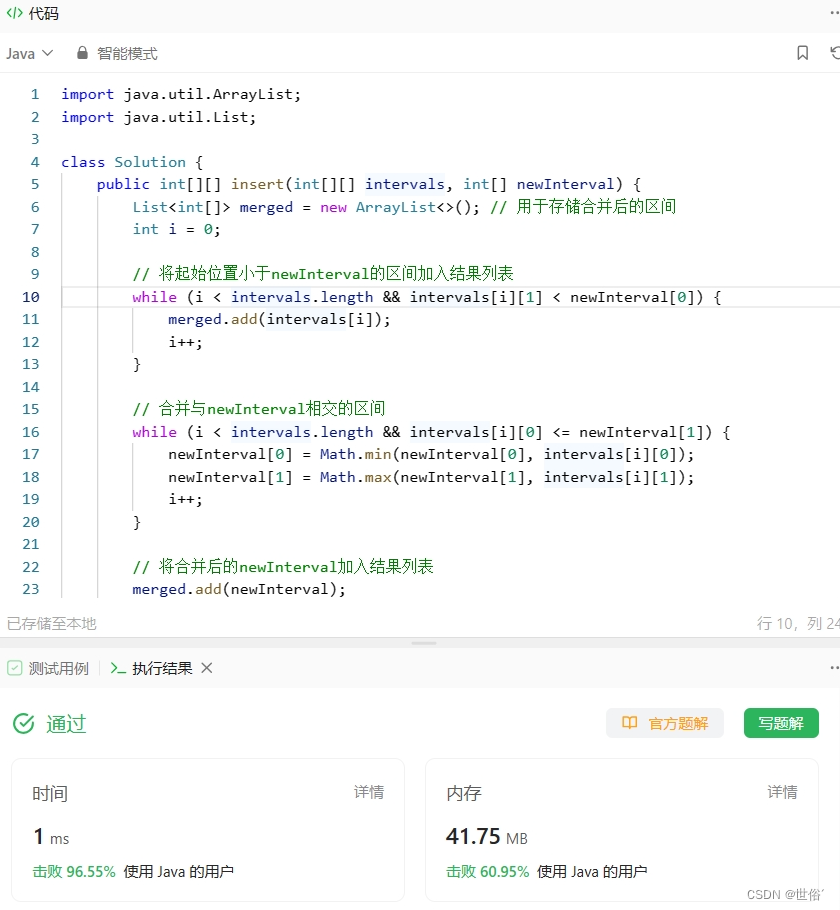
怒刷LeetCode的第23天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:贪心算法 方法二:动态规划 方法三:回溯算法 方法四:并查集 第二题 题目来源 题目内容 解决方法 方法一:排序和遍历 方法二:扫描线算法 方法…...

Golang 中的调试技巧
掌握有效的策略和工具,实现顺畅的开发 调试是每位开发人员都必须掌握的关键技能。它是识别、隔离和解决代码库中问题的过程。在 Golang 的世界中,掌握有效的调试技巧可以显著提升您的开发工作流程,并帮助您创建更可靠和健壮的应用程序。在本…...

linux 监控内存利用率
监控内存利用率 使用free来分析CPU使用信息 #!/bin/bashDATE$(date %F" "%H:%M)IP$(ifconfig eth0 |awk -F [ :] /inet addr/{print $4}) MAIL"examplemail.com"TOTAL$(free -m |awk /Mem/{print $2})USE$(free -m |awk /Mem/{print $3-$6-$7})FREE$(($TO…...
43 验证二叉搜索树
验证二叉搜索树 理解题意:验证搜索二叉树:中序遍历是升序题解1 递归(学习学习!)题解2 中序遍历(保持升序) 给你一个二叉树的根节点 root ,判断其是否是一个 有效的二叉搜索树。 有…...
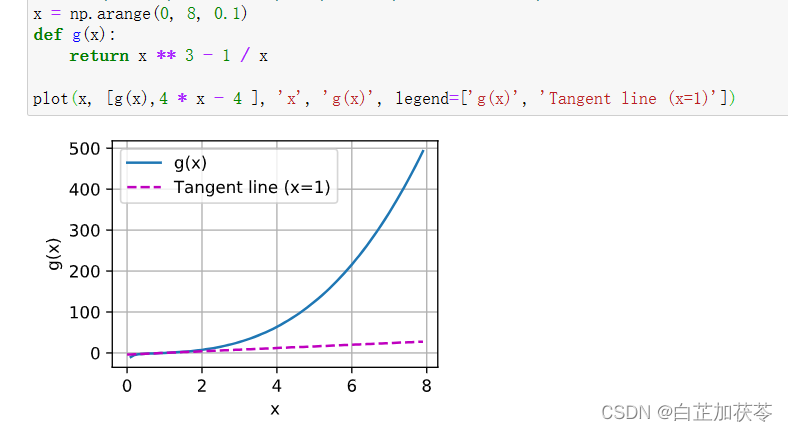
深度学习笔记之微积分及绘图
深度学习笔记之微积分及绘图 学习资料来源:微积分 %matplotlib inline from matplotlib_inline import backend_inline from mxnet import np, npx from d2l import mxnet as d2lnpx.set_np()def f(x):return 3 * x ** 2 - 4 * xdef numerical_lim(f, x, h):retur…...
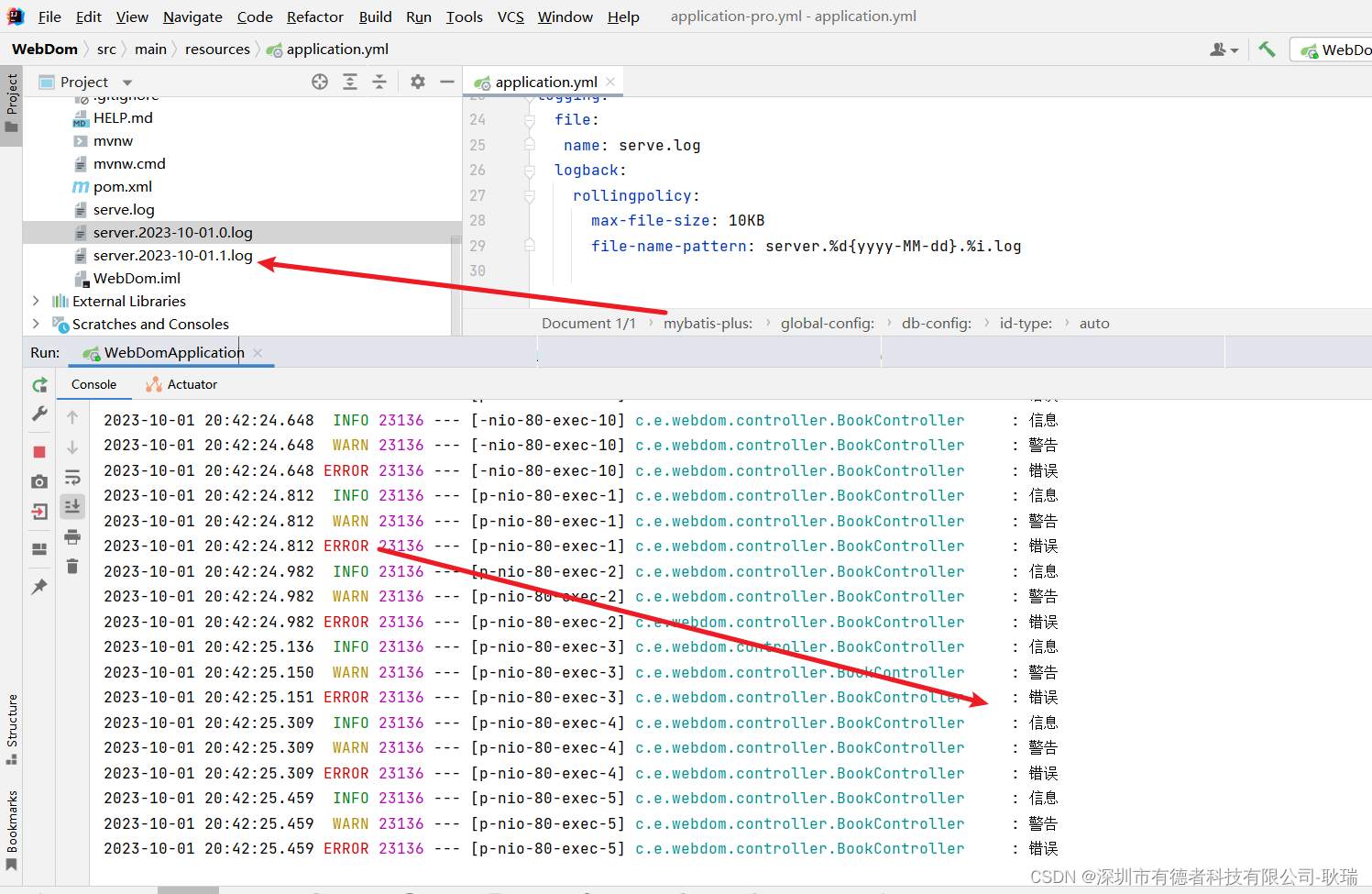
java Spring Boot按日期 限制大小分文件记录日志
上文 java Spring Boot 将日志写入文件中记录 中 我们实现另一个将控制台日志写入到 项目本地文件的效果 但是 这里有个问题 比如 我项目是个大体量的企业项目 每天会有一百万用户访问 那我每天的日志都记载同一个文件上 那不跟没记没什么区别吗? 东西怎么找&#x…...

CSS 语法
CSS 实例 CSS 规则由两个主要的部分构成:选择器,以及一条或多条声明: 选择器通常是您需要改变样式的 HTML 元素。 每条声明由一个属性和一个值组成。 属性(property)是您希望设置的样式属性(style attribute&#x…...
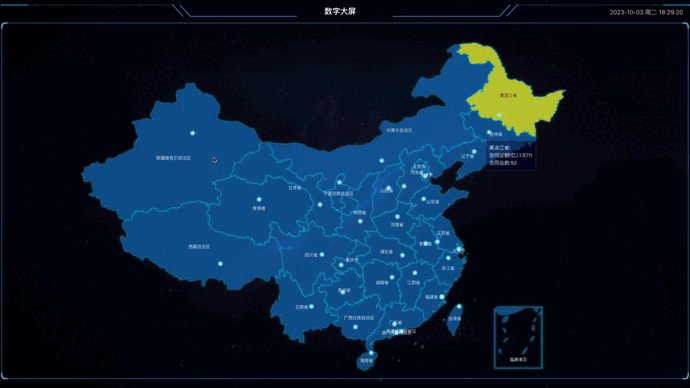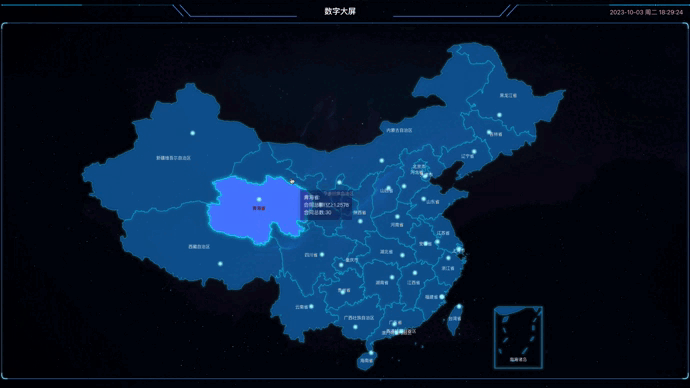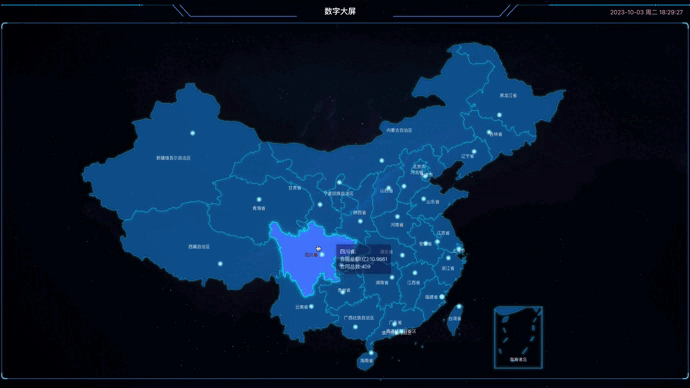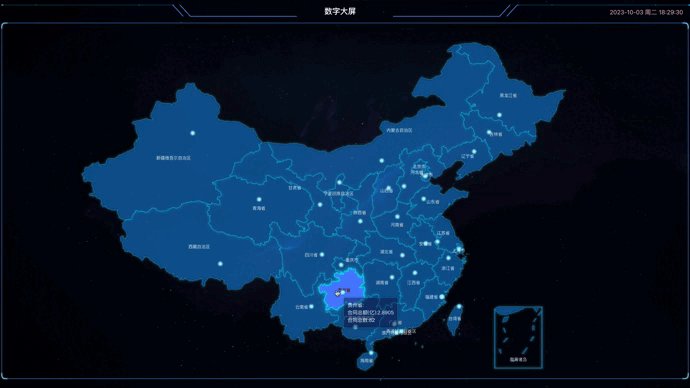
Vue3+TS+ECharts5实现中国地图数据信息显示
1.引言 最近在做一个管理系统,主要技术栈使用的是Vue3TSViteElementPlus,主要参考项目是yudao-ui-admin-vue3,其中用到ECharts5做数字大屏,展示中国地图相关信息,以此基础做一个分享,写下这篇文章。 &quo…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

Qt/C++学习系列之列表使用记录
Qt/C学习系列之列表使用记录 前言列表的初始化界面初始化设置名称获取简单设置 单元格存储总结 前言 列表的使用主要基于QTableWidget控件,同步使用QTableWidgetItem进行单元格的设置,最后可以使用QAxObject进行单元格的数据读出将数据进行存储。接下来…...

联邦学习带宽资源分配
带宽资源分配是指在网络中如何合理分配有限的带宽资源,以满足各个通信任务和用户的需求,尤其是在多用户共享带宽的情况下,如何确保各个设备或用户的通信需求得到高效且公平的满足。带宽是网络中的一个重要资源,通常指的是单位时间…...

电脑定时关机工具推荐
软件介绍 本文介绍一款轻量级的电脑自动关机工具,无需安装,使用简单,可满足定时关机需求。 工具简介 这款关机助手是一款无需安装的小型软件,文件体积仅60KB,下载后可直接运行,无需复杂配置。 使用…...
