【算法练习Day11】滑动窗口最大值前 K 个高频元素

📝个人主页:@Sherry的成长之路
🏠学习社区:Sherry的成长之路(个人社区)
📖专栏链接:练题
🎯长路漫漫浩浩,万事皆有期待
文章目录
- 滑动窗口最大值
- 前 K 个高频元素
- 总结
滑动窗口最大值
239. 滑动窗口最大值 - 力扣(LeetCode)
这道题是一道困难题,给出一个滑动窗口的长度,给出一个数组,每次滑动窗口向数组右侧滑动一个元素,要求返回一个数组该数组记录的是每次移动滑动窗口所包含的数字中最大的一个分别是什么。
不难想出暴力解法,每移动一次遍历一遍窗口记录下来当前最大的数,时间复杂度是n*k,一共n个数据,要遍历k次。那么有没有更好的方法来节省时间呢?这时我们的单调队列要登场了!
什么是单调队列?
单调队列是单调递增的队列或者单调递减的队列,但是它和优先级队列的不同之处在于,我们设计它的时候主要是要维护大值或者小值而单调递增或递减的排序是进出元素控制的并非主要思路是排序,这和优先级队列的区别还是很大的,顺便说一下单调队列通常使用双端队列做模板实现,而优先级队列底层实现是堆,也就是二叉树。
本题我们可以借助双端队列创建一个单调队列,因为c++里没有现成的单调队列,单调队列只需要三个函数,一个push一个pop一个求最大值
我们如何每次都弹出最大值呢?
其实只是需要我们将最大值调整到队列口处,而前面小的数直接pop走,其实我们要求的是每次窗口中的最大值,所以小数完全没有必要维护,直接判断弹出即可,push时我们判断队尾有没有数小于要push进来的数,如果有全部pop出来,因为是在队尾插入所以要对对尾元素做判断,在实现pop函数时判断本次要删除的元素队头有没有,没有就不删(没有的原因是之前push元素时候已经弹出了,因为为了保证取最大值的函数每次都取最大)一开始直接push前k个元素,之后采取push一个元素pop一个元素的规律,值得注意的,不是每一次都要pop,但是每一次都要调用,至于具体这一步是否真的pop了在pop函数会自动判断。
为什么会这样呢?
原因在于我们设计的单调函数里实现的时候我们需要照顾到弹出最大值这个函数,所以我们设计成这样用来方便最大值的弹出,而在真正函数调用时候,为了保证逻辑上的正确,我们每次都要调用pop这个函数,判断如果此时我们要删的元素不在队头部,那么直接往后走加入新元素即可。
class Solution {
private:class MyQueue { //单调队列(从大到小)public:deque<int> que; // 使用deque来实现单调队列// 每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。// 同时pop之前判断队列当前是否为空。void pop(int value) {if (!que.empty() && value == que.front()) {que.pop_front();}}// 如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。// 这样就保持了队列里的数值是单调从大到小的了。void push(int value) {while (!que.empty() && value > que.back()) {que.pop_back();}que.push_back(value);}// 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。int front() {return que.front();}};
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {MyQueue que;vector<int> result;for (int i = 0; i < k; i++) { // 先将前k的元素放进队列que.push(nums[i]);}result.push_back(que.front()); // result 记录前k的元素的最大值for (int i = k; i < nums.size(); i++) {que.pop(nums[i - k]); // 滑动窗口移除最前面元素que.push(nums[i]); // 滑动窗口前加入最后面的元素result.push_back(que.front()); // 记录对应的最大值}return result;}
};
时间复杂度: O(n)
空间复杂度: O(k)
前 K 个高频元素
347. 前 K 个高频元素 - 力扣(LeetCode)
这道题是考察优先级队列和语法理解
这道题是一个输出前k个高频元素的题,并不是只输出一个。所以我们想到用优先级队列来存取前k个高频元素
那么如何判断哪些是高频元素呢?
我们用unordered_map来存取每个数据出现的次数,然后用小顶堆来存取数据。
为什么要用小顶堆而不是大顶堆?
我们的思路是定义一个只能存k个元素的堆,这样我们只需要维护k个数据,减少不必要的浪费。由于哈希存储结果是unordered_map来提高效率,所以map里是无序的,我们在插入元素时候要按着map依次插入进去,而用大顶堆的话,大的数据排在前面如果map里还有更大的数据,那么之前最大的数据要先被弹出来,往复操作最后只剩下频率最低的k个元素。而使用小顶堆那么每次弹出最小元素,加进来较大元素,最后沉淀下来的是k个高频数据。当然如果使用的是map的话可能就不需要考虑这些问题,因为是排好序的。
按着刚才的思路写出代码
class Solution {
public:// 小顶堆class mycomparison {public:bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {return lhs.second > rhs.second;}};vector<int> topKFrequent(vector<int>& nums, int k) {// 要统计元素出现频率unordered_map<int, int> map; // map<nums[i],对应出现的次数>for (int i = 0; i < nums.size(); i++) {map[nums[i]]++;}// 对频率排序// 定义一个小顶堆,大小为kpriority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que;// 用固定大小为k的小顶堆,扫面所有频率的数值for (unordered_map<int, int>::iterator it = map.begin(); it != map.end(); it++) {pri_que.push(*it);if (pri_que.size() > k) { // 如果堆的大小大于了K,则队列弹出,保证堆的大小一直为kpri_que.pop();}}// 找出前K个高频元素,因为小顶堆先弹出的是最小的,所以倒序来输出到数组vector<int> result(k);for (int i = k - 1; i >= 0; i--) {result[i] = pri_que.top().first;pri_que.pop();}return result;}
};
注意:把map的两个数据都放到堆里,然后根据二元组的第二个关键词来进行排序,这样我们在进行最后一步转化为数组的时候,才能根据频率找到对应的数据,缺一不可
总结
今天我们完成了滑动窗口最大值、前 K 个高频元素两道题目,相关的思想需要多复习回顾。接下来,我们继续进行算法练习·。希望我的文章和讲解能对大家的学习提供一些帮助。
当然,本文仍有许多不足之处,欢迎各位小伙伴们随时私信交流、批评指正!我们下期见~

相关文章:

【算法练习Day11】滑动窗口最大值前 K 个高频元素
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:练题 🎯长路漫漫浩浩,万事皆有期待 文章目录 滑动窗口最大值前 K 个高频…...
华为云HECS云服务器docker环境下安装nginx
前提:有一台华为云服务器。 华为云HECS云服务器,安装docker环境,查看如下文章。 华为云HECS安装docker-CSDN博客 一、拉取镜像 下载最新版Nginx镜像 (其实此命令就等同于 : docker pull nginx:latest ) docker pull nginx查看镜像 dock…...

GET 和 POST的区别
GET 和 POST 是 HTTP 请求的两种基本方法,要说它们的区别,接触过 WEB 开发的人都能说出一二。 最直观的区别就是 GET 把参数包含在 URL 中,POST 通过 request body 传递参数。 你可能自己写过无数个 GET 和 POST 请求,或者已经看…...
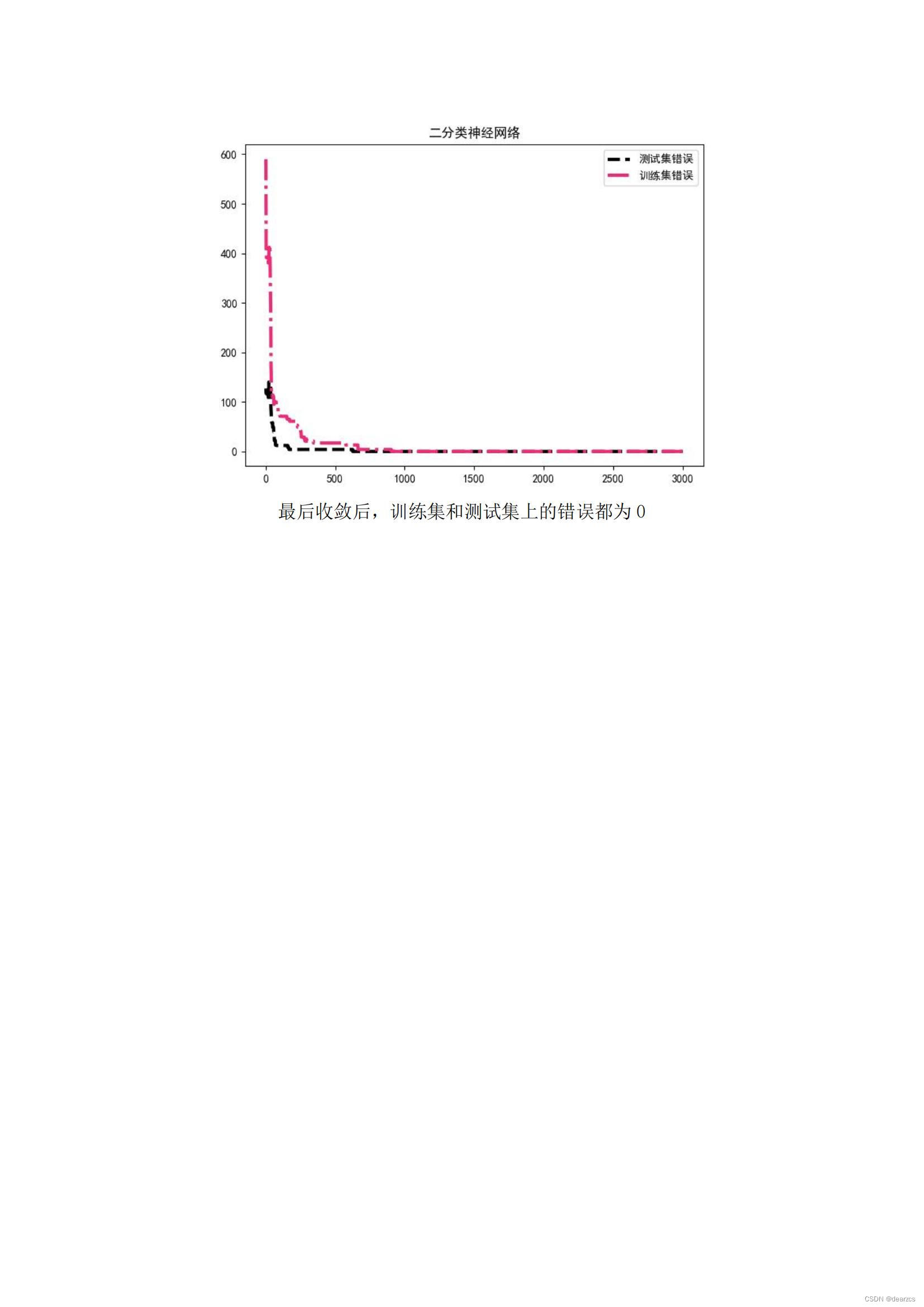
机器学习(监督学习)笔记
目录 总览笔记内容线性回归梯度下降特征缩放多输出线性回归 逻辑回归二分类与逻辑回归分类任务的性能指标(召回率,精度,F1分数等)支持向量机SVMK近邻朴素贝叶斯分类器朴素贝叶斯分类器进阶多分类逻辑回归二分类神经网络多分类神经…...
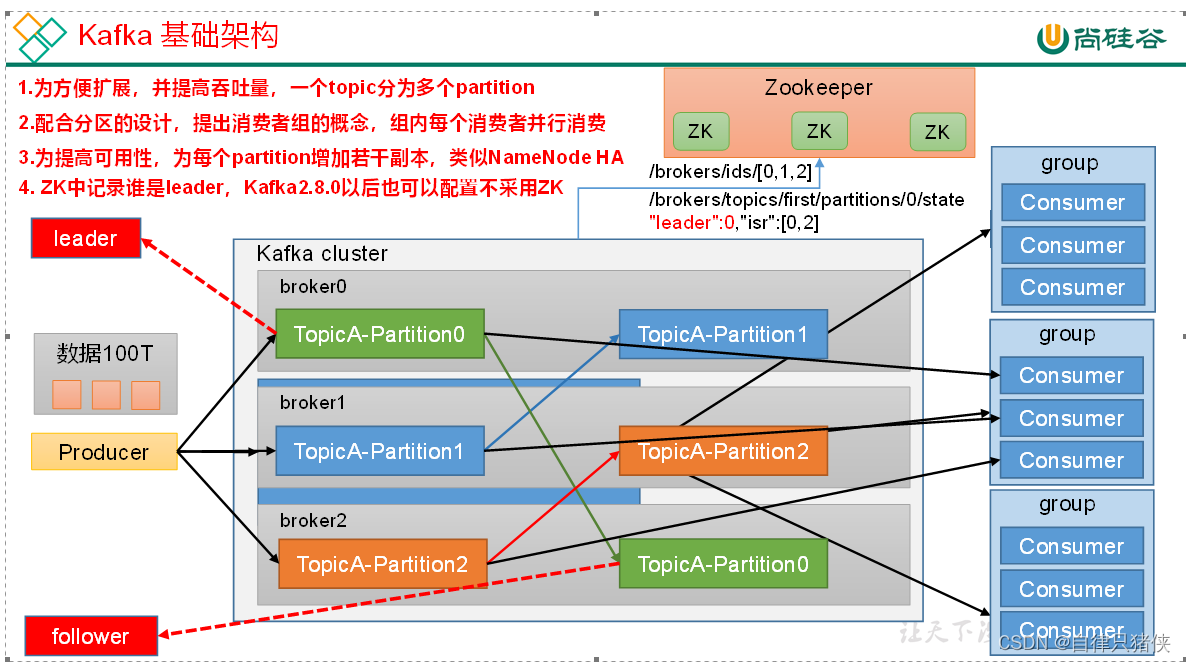
科普rabbitmq,rocketmq,kafka三者的架构比较
对比 架构对比 从架构可以看出三者有些类似,但是在细节上有很多不同。下面我们就从它们的各个组件,介绍它们: RabbitMQ,是一种开源的消息队列中间件。下面是RabbitMQ中与其相关的几个概念: 1.生产者(P…...
)
加密货币交易技巧——地利(二)
EMA指标 针对资金体量大的代币,做现货交易或低倍合约,可参考以下指标: 1.指标介绍:EMA,移动平均线指标,这里只分享中长线用法,非常实用且准确率超高 2.适用群体:适用于现货或低倍…...

服务网关Gateway_微服务中的应用
没有服务网关 问题: 地址太多安全性管理问题 为什么要使用服务网关 网关是微服务架构中不可或缺的部分。使用网关后,客户端和微服务之间的网络结构如下。 注意: 网关统一向外部系统(如访问者、服务)提供REST API。在Sp…...

2G大小的GPU对深度学习的加速效果如何?
训练数据情况 总共42776张224*224*3张图片 Found 42776 files belonging to 9 classes. Using 12833 files for training. 模型参数情况 Total params: 10,917,385 Trainable params: 10,860,745 Non-trainable params: 56,640 batch-size:12 GPU信息 NVIDIA GeForce GT 7…...

intel 一些偏门汇编指令总结
intel 汇编手册下载链接:https://www.intel.com/content/www/us/en/developer/articles/technical/intel-sdm.html LDS指令: 手册中可以找到 位于 3-588 根据手册内容猜测:lds r16 m16:16 的作用,是把位于 [m16:16] 内存地址的数…...

python 多个proto文件import引用时出现ModuleNotFoundError错误
问题描述 my_proto文件夹里有两个proto文件,book.proto想要引用person.proto文件中的Person,如下 book.proto syntax "proto2";import "person.proto"; // 导入person.proto文件message Book {optional string name 1;optional …...
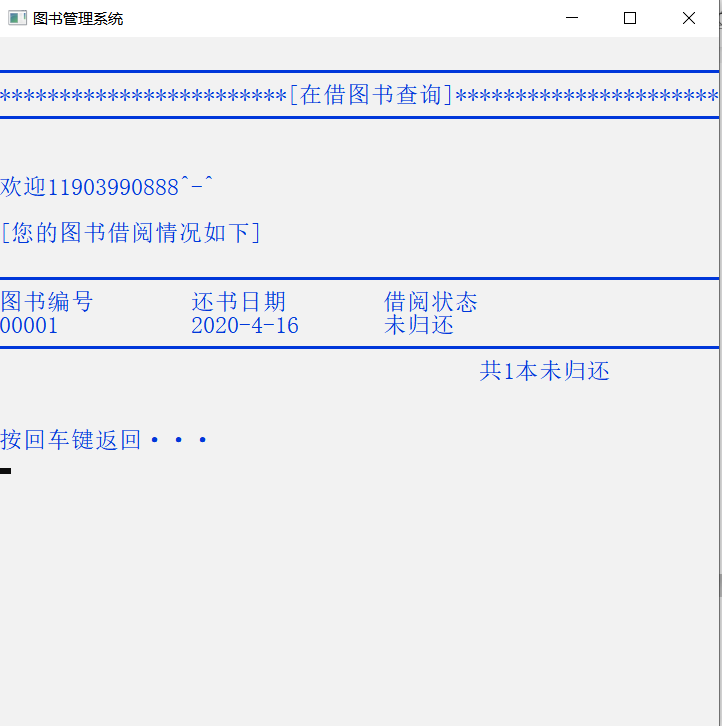
C语言图书管理系统
一、 系统概述 图书管理系统是一个用C语言编写的软件系统,旨在帮助图书馆或图书机构管理其图书馆藏书和读者信息。该系统提供了一套完整的功能,包括图书录入、借阅管理、归还管理、读者管理、图书查询、统计报表等。 二、 系统功能 2.1 图书录入 管理…...

归并排序及其非递归实现
个人主页:Lei宝啊 愿所有美好如期而遇 目录 归并排序递归实现 归并排序非递归实现 归并排序递归实现 图示: 代码: 先分再归并,像是后序一般。 //归并排序 void MergeSort(int* arr, int left, int right) {int* temp (int…...
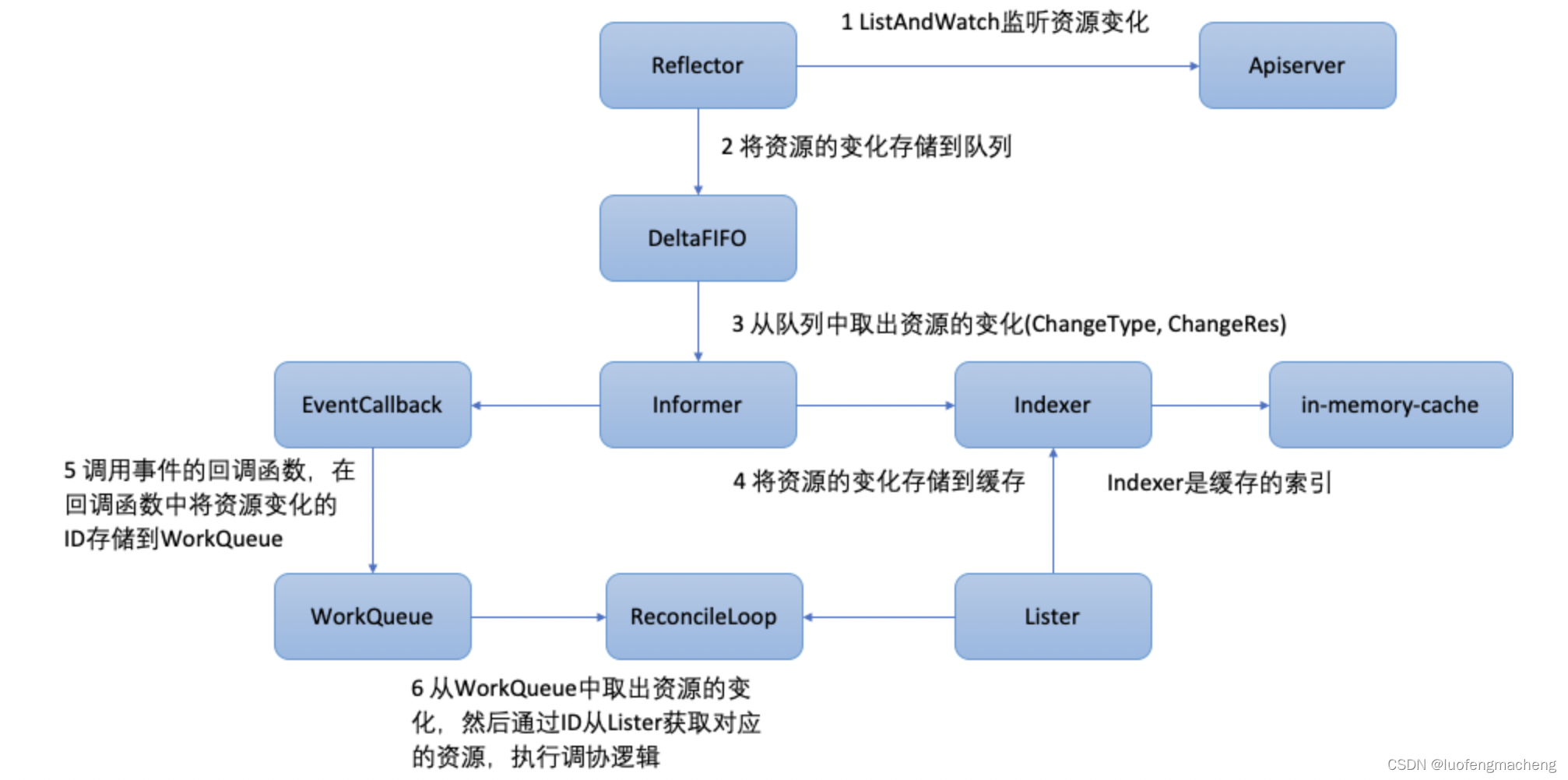
【kubernetes】kubernetes中的Controller
1 什么是Controller? kubernetes采用了声明式API,与声明式API相对应的是命令式API: 声明式API:用户只需要告诉期望达到的结果,系统自动去完成用户的期望命令式API:用户需要关注过程,通过命令一…...

RabbitMQ-死信队列
接上文 RabbitMQ-java使用消息队列 1 死信队列简介 死信队列模式实际上本质是一个死信交换机绑定的死信队列,当正常队列的消息被判定为死信时,会被发送到对应的死信交换机,然后再通过交换机发送到死信队列中,死信队列也有对应的消…...

ElasticSearch - 基于 DSL 、JavaRestClient 实现数据聚合
目录 一、数据聚合 1.1、基本概念 1.1.1、聚合分类 1.1.2、特点 1.2、DSL 实现 Bucket 聚合 1.2.1、Bucket 聚合基础语法 1.2.2、Bucket 聚合结果排序 1.2.3、Bucket 聚合限定范围 1.3、DSL 实现 Metrics 聚合 1.4、基于 JavaRestClient 实现聚合 1.4.1、组装请求 …...
什么是数学建模(mooc笔记)
什么是数学建模 前提:我们数学建模国赛计划选择C题,故希望老师的教学中侧重与C题相关性大的模型及其思想进行培训。之后的学习内容中希望涉及以下知识点: logistic回归相关知识点。如:用法、适用、限制范围等。精学数学建模中常…...
基于SpringBoot的流浪动物管理系
基于SpringBoot的流浪动物管理系的设计与实现,前后端分离 开发语言:Java数据库:MySQL技术:SpringBootMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 首页 后台登陆界面 管理员界面 摘要 基于Spring Boot的…...
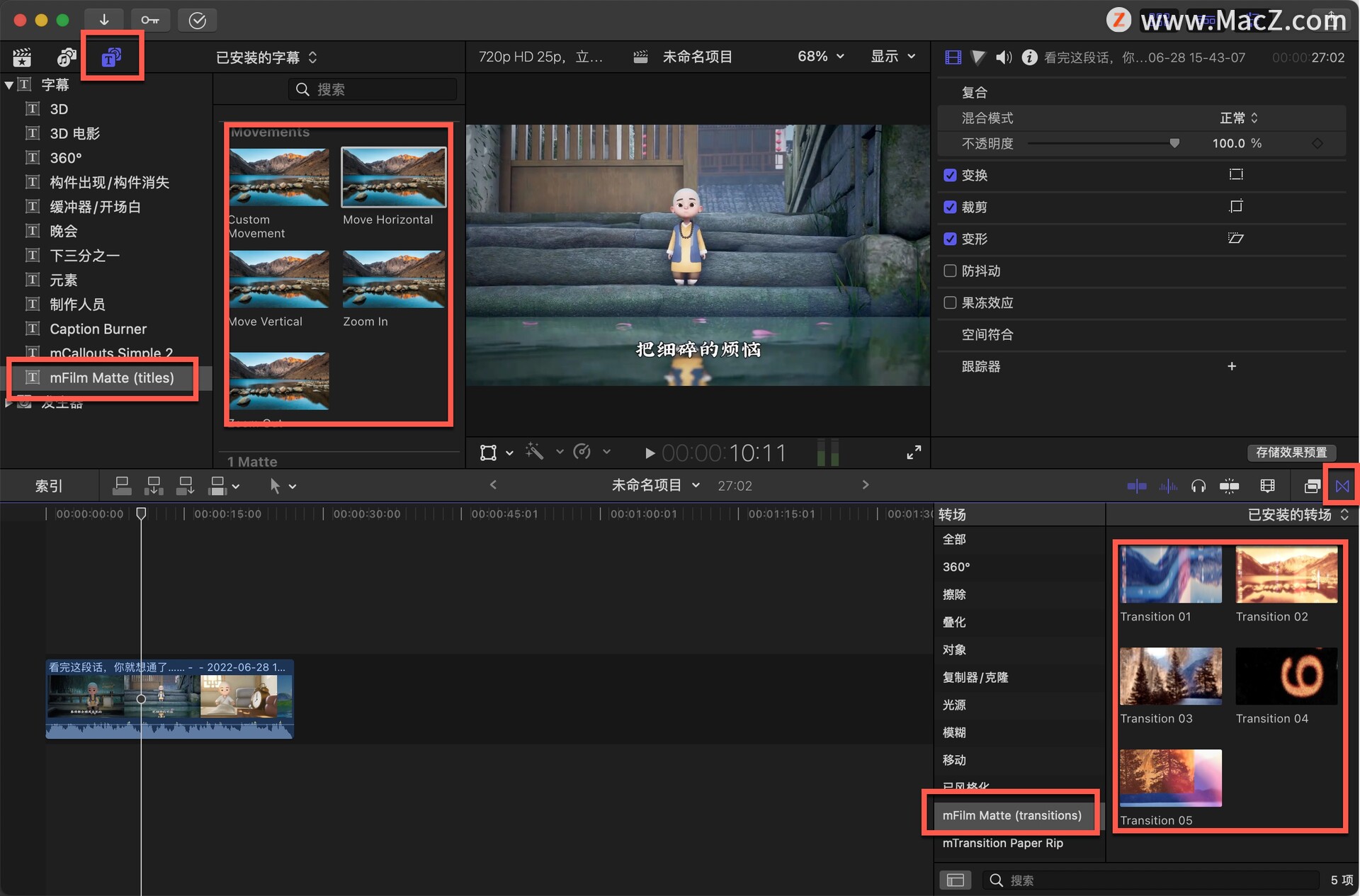
fcpx插件:82种复古电影胶卷框架和效果mFilm Matte
无论您是在制作音乐剪辑、私人假期视频还是大型广告活动,这个专业的插件都将帮助您为您的镜头赋予真正的电影角色。 复古效果在任何视频中都能立即识别出来,增添了感伤的复古氛围,并使镜头更具说服力。使用 mFilm Matte 轻松实现这些特征&…...
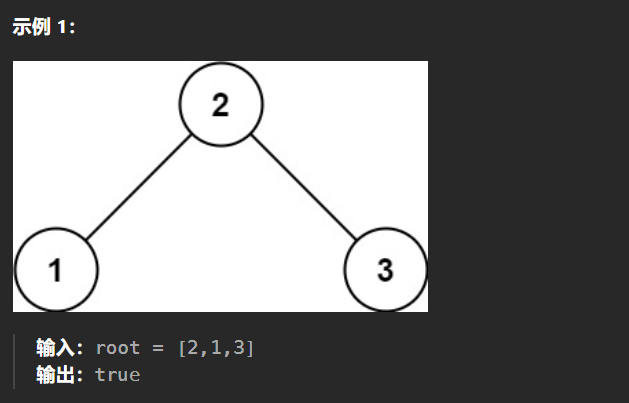
【LeetCode热题100】--98.验证二叉搜索树
98.验证二叉搜索树 给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。 有效 二叉搜索树定义如下: 节点的左子树只包含 小于 当前节点的数。节点的右子树只包含 大于 当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。 由于二…...

wxpython:wx.grid 表格显示 Excel xlsx文件
pip install xlrd xlrd-1.2.0-py2.py3-none-any.whl (103 kB) 摘要: Library for developers to extract data from Microsoft Excel (tm) spreadsheet files pip install wxpython4.2 wxPython-4.2.0-cp37-cp37m-win_amd64.whl (18.0 MB) Successfully installed wxpython-4.…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...
