计组——I/O方式
一、程序查询方式
CPU不断轮询检查I/O控制器中“状态寄存器”,检测到状态为“已完成”之后,再从数据寄存器取出输入数据。

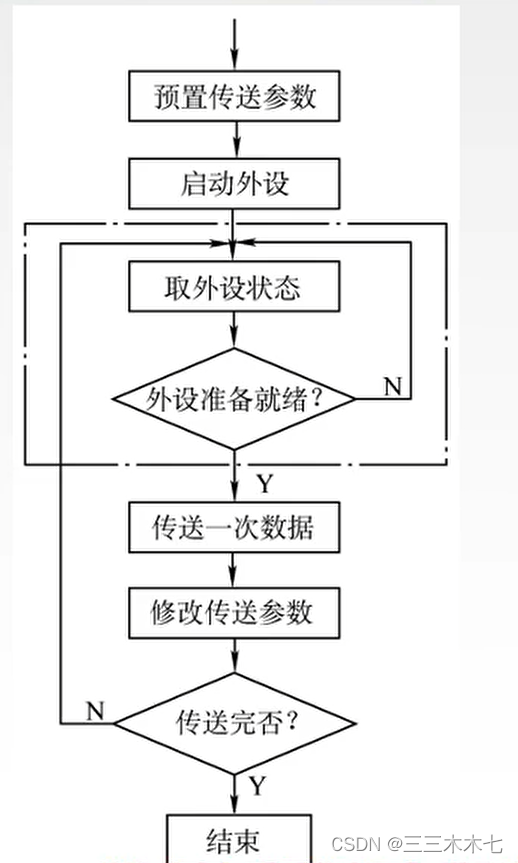
过程:
1.CPU执行初始化程序,并预置传送参数;设置计数器、设置数据首地址。
2. 向I/O接口发送命令字,启动I/O设备
3.CPU从接口读取设备状态信息
4.CPU不断查询I/O设备状态,直到外设准备就绪
5.传送一次数据,一般为一个字
6.修改传送参数,修改地址和计数器参数

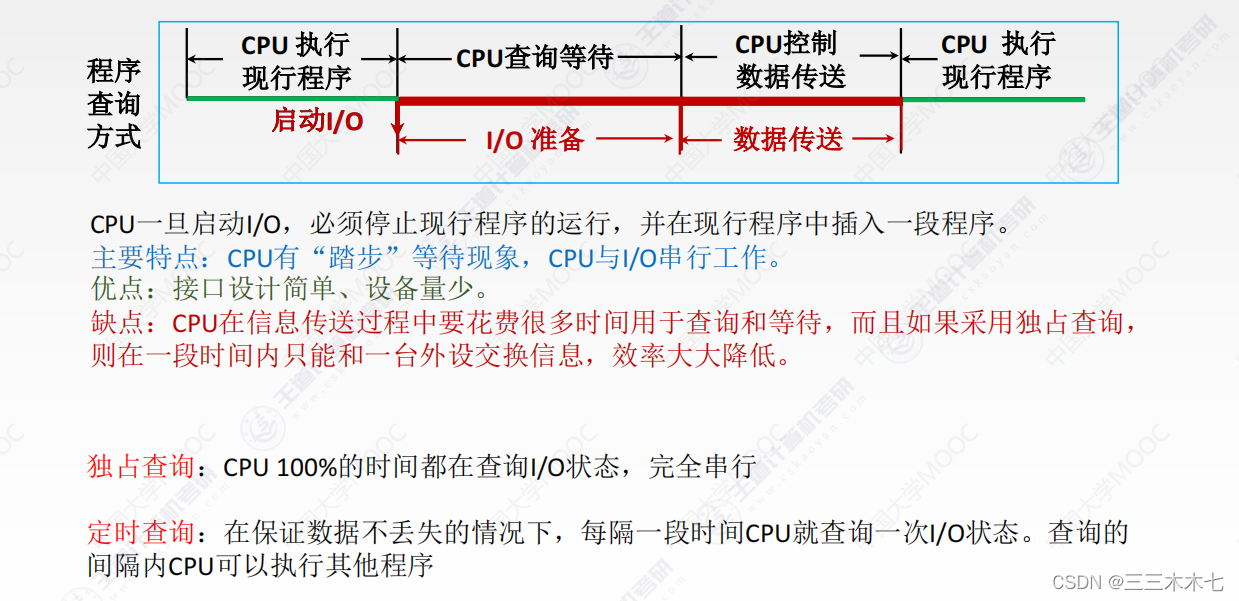
⭐CPU一旦启动I/O必须停止现行程序的运行,并在现行程序中插入一段程序。
主要特点:CPU有“踏步”等待的现象,CPU与I/O串行工作。
二、程序中断方式
1.中断的概念
程序中断是指在计算机执行现行程序的过程中,出现某些急需处理的异常情况或特殊请求,CPU暂时中止现行程序,而转去对这些异常情况或特殊请求进行处理,在处理完毕后CPU又自动返回到现行程序的断点处,继续执行原程序。
2.中断的工作流程
中断请求→中断响应→中断处理
(1)中断请求
中断源向CPU发送中断请求信号。
(2)中断响应
响应中断的条件。
中断判优:多个中断源同时提出中断请求的话需要进行中断判优。
(3)中断处理
中断隐指令。
中断服务程序。
3.中断请求标志
为了记录中断事件并区分不同的中断源,中断系统需要对每个中断源设置中断请求标记触发器INTR。
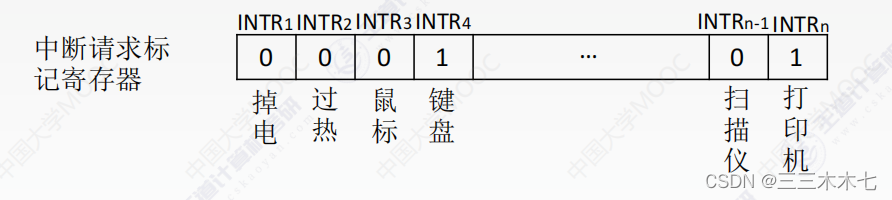
CPU响应中断的时间,是在每条指令执行阶段的结束时刻。
4.中断判优优先级设置

5.中断处理过程
5.1 隐指令
中断隐指令,不是一条具体的指令,而是CPU检测到中断请求时自动完成的一系列动作。
主要任务:
(1)关中断
(2)保存断点
(3)引出中断服务程序
5.2 向量地址
确定中断服务程序它的入口地址的方法有两个:硬件向量法、软件查询法
(1)硬件向量法
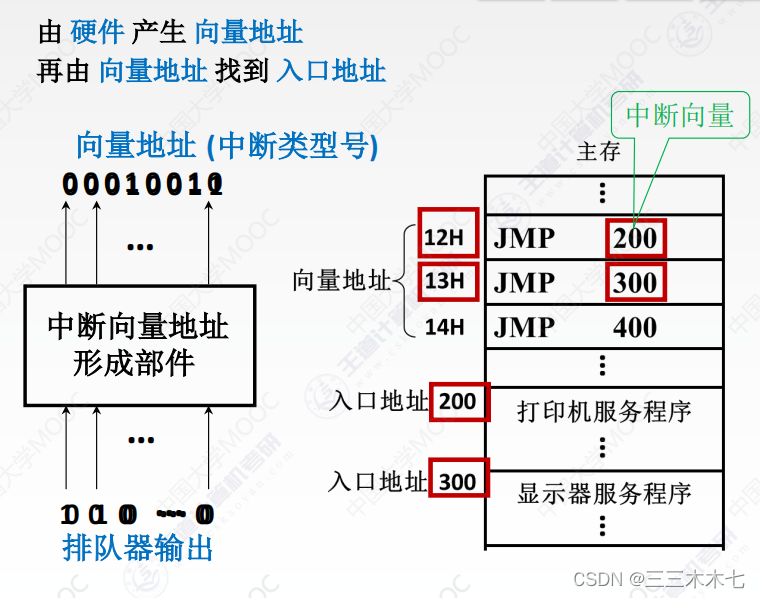
第一步:得到中断类型号
首先,根据某个中断请求信号通过硬件,得到对应的中断向量的保存地址。
(中断向量,把指向中断服务程序起始地址的地址信息称为中断向量)
第二步:得到中断服务程序的入口地址
向量地址对应的主存里保存了JMP无条件转移指令,这个无条件转移指令指明了当前中断请求对应的中断服务程序的入口地址 。
5.3 中断服务程序
(1)保护现场
(2)中断服务
(3)恢复现场
(4)中断返回
6.多重中断
6.1 中断屏蔽字
“1” 表示屏蔽该中断的源的请求,即继续执行当前正在执行的中断。
“0” 表示正常申请,停止当前程序去执行新的中断程序。
三、DMA方式
相关文章:

计组——I/O方式
一、程序查询方式 CPU不断轮询检查I/O控制器中“状态寄存器”,检测到状态为“已完成”之后,再从数据寄存器取出输入数据。 过程: 1.CPU执行初始化程序,并预置传送参数;设置计数器、设置数据首地址。 2. 向I/O接口发…...

jsbridge实战2:Swift和h5的jsbridge通信
[[toc]] demo1: 文本通信 h5 -> app 思路: h5 全局属性上挂一个变量app 接收这个变量的内容关键API: navigation代理 navigationAction.request.url?.absoluteString // 这个变量挂载在 request 的 url 上 ,在浏览器实际无法运行,因…...

集合原理简记
HashMap 无论在构造函数是否指定数组长度,进行的都是延迟初始化 构造函数作用: 阈值:threshold,每次<<1 ,数组长度 负载因子 无参构造:设置默认的负载因子 有参:可以指定初始容量或…...

机器学习的超参数 、训练集、归纳偏好
一、介绍 超参数(Hyperparameters)和验证集(Validation Set)是机器学习中重要的概念,用于调整模型和评估其性能。 超参数: 超参数是在机器学习模型训练过程中需要手动设置的参数,而不是从数据…...
Leetcode1071. 字符串的最大公因子(三种方法,带详细解析)
Leetcode1071. 字符串的最大公因子 对于字符串 s 和 t,只有在 s t … t(t 自身连接 1 次或多次)时,我们才认定 “t 能除尽 s”。 给定两个字符串 str1 和 str2 。返回 最长字符串 x,要求满足 x 能除尽 str1 且 x 能…...

如何像人类一样写HTML之图像标签,超链接标签与多媒体标签
文章目录 前言一、图像标签1.1 什么是图像标签?2.2 如何使用图像标签? 二、超链接标签2.1 什么是超链接标签?2.2 如何使用超链接标签? 三、多媒体标签3.1 什么是多媒体标签?3.2 如何使用多媒体audio标签?3.…...

1300*C. Rumor(并查集贪心)
解析: 并查集,求每个集合的最小费用。 每次合并集合的时候,根节点保存当前集合最小的费用。 #include<bits/stdc.h> using namespace std; #define int long long const int N1e55; int n,m,a[N],p[N],cnt[N]; int find(int x){retur…...
)
python实用小代码(数据分析向)
一、python实现31省市名称替换 首先定义了一个字典province_dict,其中包含每个省市的无缩写名称与其标准名称之间的映射。然后,我们使用map()函数将每个省市名称从无缩写名称转换为标准名称,并将结果存储在新列省市标准名称中。 province_di…...

【oncmdmsg 鼠标】2023/8/19 上午9:50:14
2023/8/19 上午9:50:14 oncmdmsg 鼠标 2023/8/19 上午9:50:22 抱歉,您提到的 “oncmdmsg” 和 “鼠标” 是什么?请提供更多上下文信息,我将尽力帮助您。 2023/8/19 上午9:51:43 OnCmdMsg 2023/8/19 上午9:52:21 “OnCmdMsg” 是一个在 MFC (Microsoft Foundation Cla…...

插入排序:简单而有效的排序方法
在计算机科学中,排序算法是一个重要且常见的主题,它们用于对数据进行有序排列。插入排序(Insertion Sort)是其中一个简单但有效的排序算法。本文将详细解释插入排序的原理和步骤,并提供Java语言的实现示例。 插入排序的…...

OpenGL之光照贴图
我们需要拓展之前的系统,引入漫反射和镜面光贴图(Map)。这允许我们对物体的漫反射分量和镜面光分量有着更精确的控制。 漫反射贴图 我们希望通过某种方式对物体的每个片段单独设置漫反射颜色。我们仅仅是对同样的原理使用了不同的名字:其实都是使用一张覆盖物体的图像,让我…...

隐私交易成新刚需,Unijoin 凭什么优势杀出重围?
随着区块链技术的普及和发展,全球加密货币用户在持续增长,根据火币研究院公布的数据,2022年全球加密用户已达到 3.2亿人,目前全球人口总数超过了 80亿,加密货币用户渗透率已达到了 4%。 尤其是在 2020 年开启的 DeFi 牛…...
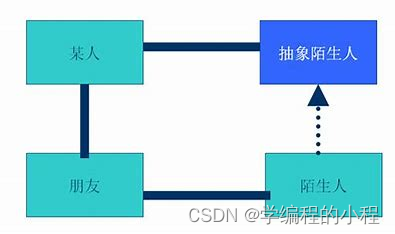
小谈设计模式(12)—迪米特法则
小谈设计模式(12)—迪米特法则 专栏介绍专栏地址专栏介绍 迪米特法则核心思想这里的“朋友”指当前对象本身以参数形式传入当前对象的对象当前对象的成员变量直接引用的对象目标 Java程序实现程序分析 总结 专栏介绍 专栏地址 link 专栏介绍 主要对目…...

Foxit PDF
Foxit PDF 福昕PDF 软件,可以很好的编辑PDF文档。 调整PDF页面大小 PDF文档中,一个页面大,一个页面小 面对这种情况,打开Foxit PDF 右键单击需要调整的页面,然后选择"调整页面大小". 可以选择…...

《Python趣味工具》——ppt的操作(刷题版)
前面我们对PPT进行了一定的操作,并将其中的文字提取到了word文档中。现在就让我们来刷几道题巩固巩固吧! 文章目录 1. 查看PPT(上)2. 查看PPT(中)3. 查看PPT(下)4. PPT的页码5. 大学…...

实战型开发--3/3,clean code
编程的纯粹 hmmm,一开始在这个环节想聊一些具体的点,其实也就是《clean code》这本书中的点,但这个就还是更流于表面; 因为编码的过程,就更接近于运动员打球,艺术家绘画,棋手下棋的过程&#x…...
家用无线路由器如何用网线桥接解决有些房间无线信号覆盖不好的问题(低成本)
环境 光猫ZXHN F677V9 水星MW325R 无线百兆路由器 100M宽带,2.4G无线网络 苹果手机 安卓平板电脑 三室一厅94平 问题描述 家用无线路由器如何用网线桥接解决有些房间无线信号不好问题低成本解决,无线覆盖和漫游 主路由器用的运营商的光猫自带无…...
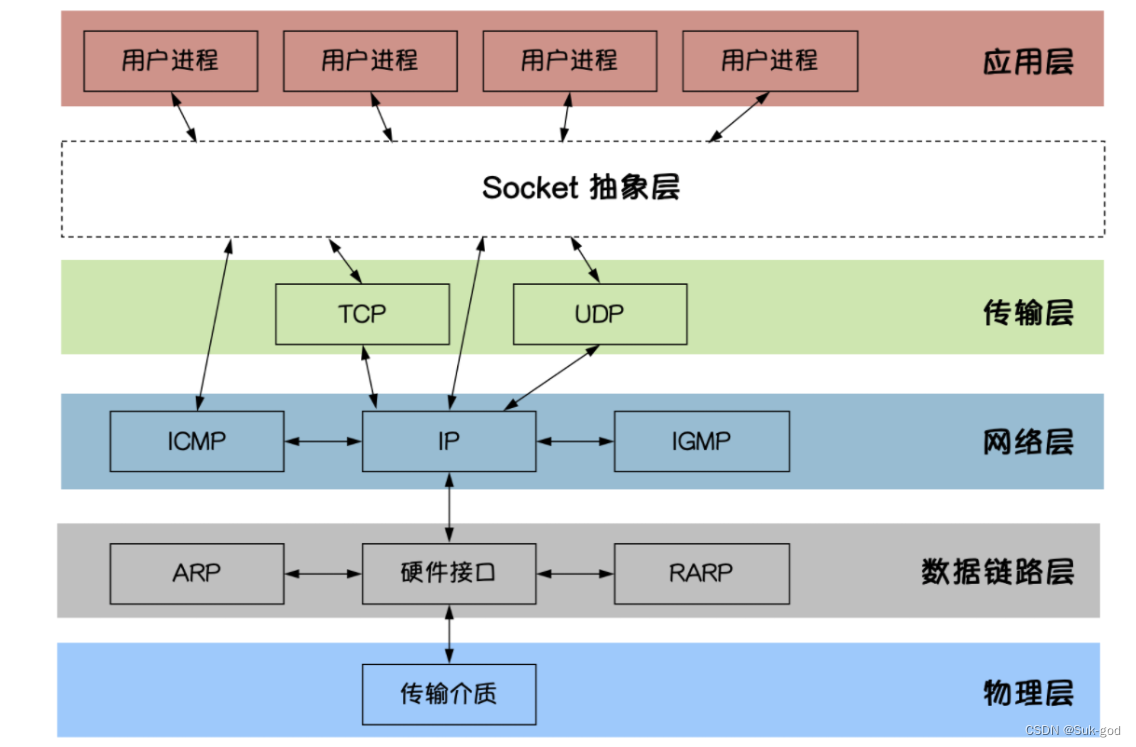
【Golang】网络编程
网络编程 网络模型介绍 OSI七层网络模型 在软件开发中我们使用最多的是上图中将互联网划分为五个分层的模型: 物理层数据链路层网络层传输层应用层 物理层 我们的电脑要与外界互联网通信,需要先把电脑连接网络,我们可以用双绞线、光纤、…...

使用策略模式优化多重if/else
一、为什么需要策略模式? 作为前端程序员,我们经常会遇到这样的场景,例如 进入一个营销活动页面,会根据后端下发的不同 type ,前端页面展示不同的弹窗。 async getMainData() {try {const res await activityQuery()…...
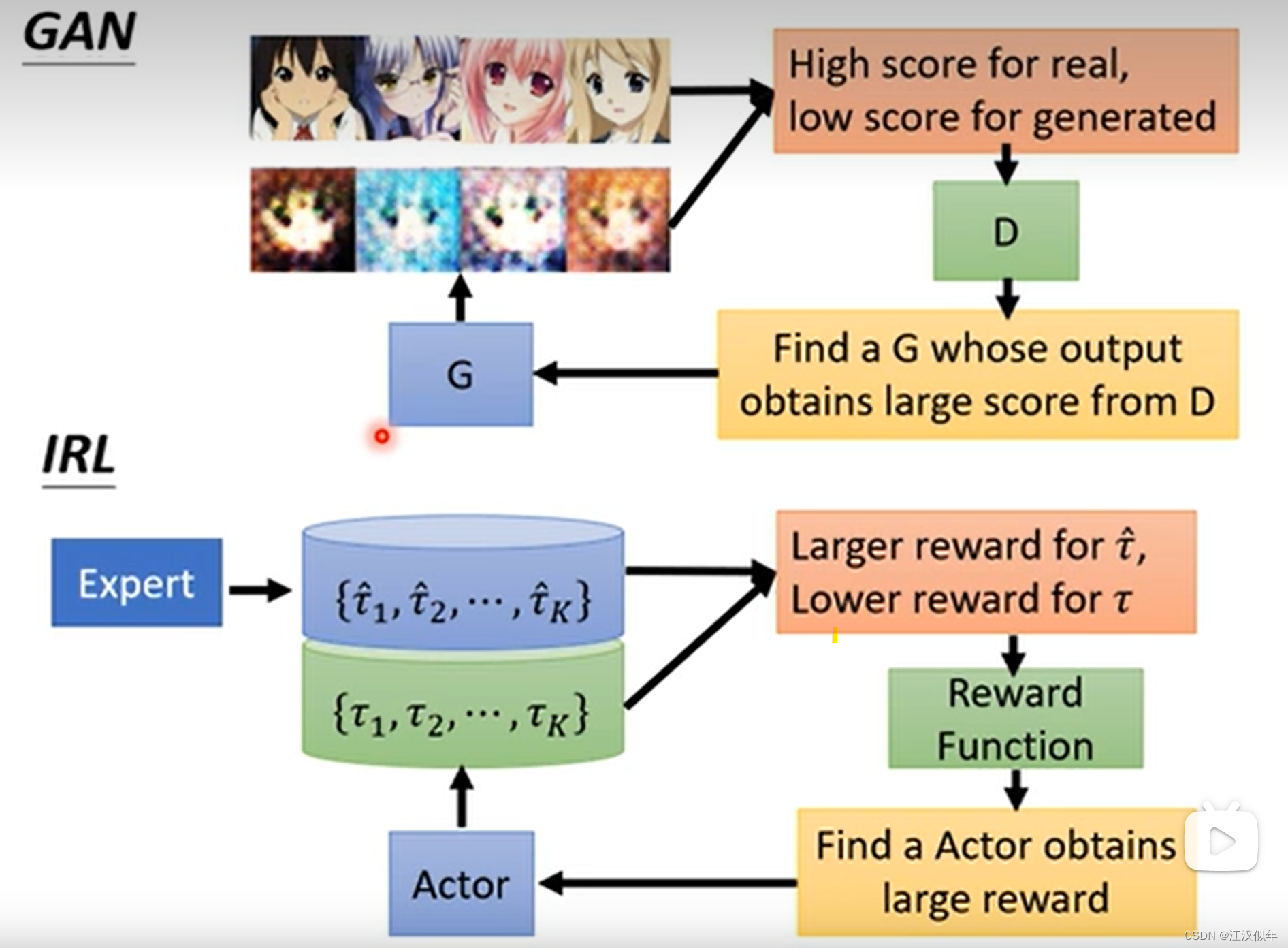
逆强化学习
1.逆强化学习的理论框架 1.teacher的行为被定义成best 2.学习的网络有两个,actor和reward 3.每次迭代中通过比较actor与teacher的行为来更新reward function,基于新的reward function来更新actor使得actor获得的reward最大。 loss的设计相当于一个排序问…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
