【图论】判环问题
(未更新完、做到相关题再更新相关部分
文章目录
- 无向图判断有无环并输出环上点
无向图判断有无环并输出环上点
例题:H. Mad City
利用变种拓扑排序,先把度为1的点存入队中,每次取出队头,遍历邻接点,再将该条边删除也就是将邻接点度数减一,直至对空,然后所有度数不为0的点都是在环上的点,输出即可
code
for (int i = 0; i < n; i ++ )
{int x, y;cin >> x >> y;add(x, y), add(y, x);ind[x] ++, ind[y] ++ ;
}function<void()> topsort = [&]()
{queue<int> q;for (int i = 1; i <= n; i ++ )if (ind[i] == 1) q.push(i);while (q.size()){int u = q.front();q.pop();for (int i = h[u]; ~i; i = ne[i]){int v = e[i];if (-- ind[v] == 1) q.push(v);}}
};topsort();for (int i = 1; i <= n; i ++ )if (ind[i] > 1) ans = true;
相关文章:

【图论】判环问题
(未更新完、做到相关题再更新相关部分 文章目录 无向图判断有无环并输出环上点 无向图判断有无环并输出环上点 例题:H. Mad City 利用变种拓扑排序,先把度为1的点存入队中,每次取出队头,遍历邻接点,再将该…...

将3D MAX设计模型导入NX1988
将3D MAX设计模型导入NX1988 概述导入流程导出喜欢的模型对模型进行修改模型贴图 概述 一般家装设计都不会用NX之类的产品设计软件,也没有通用的文件格式可以互相转换,本文的目的是将从网上下载的一些设计较好的3D MAX模型导入到NX软件中借用࿰…...

操作系统原理实验三:页面调度算法程序
实验三:页面调度算法程序 课程名称:操作系统原理 项目名称:页面调度算法程序 实验(实训)类型:验证性实验 实验(实训)课时:2 [目的和要求] 目的: 加深对请…...
QT实现tcp服务器客户端
服务器.cpp #include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);//实例化一个服务器server new QTcpServer(this);// 此时,服务器已经成功进入监听状态…...

tcp拥塞控制原理
18.3 拥塞控制 我们在向对端发送数据时,并不是一股脑子任意发送,因为TCP建立连接后,就是建立了一根管道,这跟管道上,实际上有很多的工作设备,比如路由器和交换机等等,他们都会对接收到的TCP包进…...

【C++设计模式之简单工厂模式】分析及示例
简介 简单工厂模式是一种常见的设计模式,用于创建多种相似对象的实例,属于创建型。 它通过一个工厂类来解耦客户端代码和对象的创建过程,使得客户端无需直接和具体的产品类交互,而只需要通过工厂类获取所需的产品实例即可。 原理…...

云原生定义整理
云原生定义整理 Pivotal 是云原生应用的提出者,并推出了 Pivotal Cloud Foundry 云原生应用平台和 Spring 开源 Java 开发框架,成为云原生应用架构中先驱者和探路者。 Pivotal最初的定义 Pivotal公司的Matt Stine在2015年写了一本叫做<<迁移到云…...
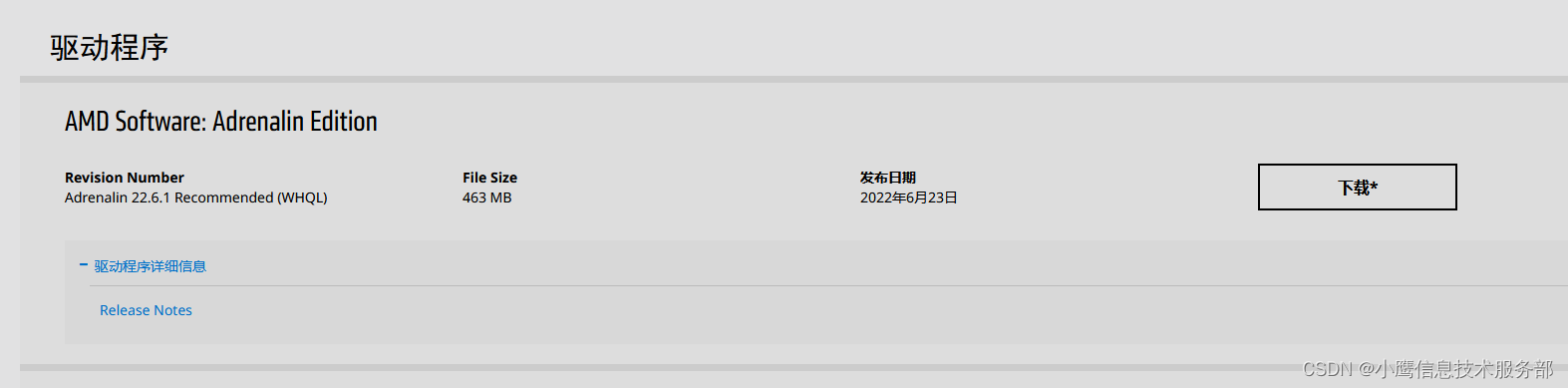
华硕X555YI, Win11下无法调节屏幕亮度
翻出一个旧电脑华硕X555YI,装Win11玩,已经估计到会有一些问题。 果然,装完之后,发现屏幕无法调节亮度。试了网上的一些方法,比如修改注册表等,无效。 估计是显卡比较老,哪里没兼容。然后用驱动…...

踩坑 | vue动态绑定img标签src属性的一系列报错
文章目录 踩坑 | vue项目运行后使用require()图片也不显示问题描述vue中动态设置img的src不生效问题的原因require is not defined 解决办法1:src属性直接传入地址解决办法2 踩坑 | vue项目运行后使用require()图片也不显示 问题描述 在网上查阅之后,发…...

强化学习环境 - robogym - 学习 - 1
强化学习环境 - robogym - 学习 - 1 项目地址 https://github.com/openai/robogym 为什么选择 robogym 自己的项目需要做一些机械臂 table-top 级的多任务操作 robogym 基于 mujoco 搭建,构建了一个仿真机械臂桌面物体操作(pick-place、stack、rearr…...

如果在 Mac 上的 Safari 浏览器中无法打开网站
使用网络管理员提供的信息更改代理设置。个人建议DNS解析,设置多个例如114.114.114.114 8.8.8.8 8.8.4.4 如果打不开网站,请尝试这些建议。 在 Mac 上的 Safari 浏览器 App 中,检查页面无法打开时出现的信息。 这可能会建议解决问题的…...
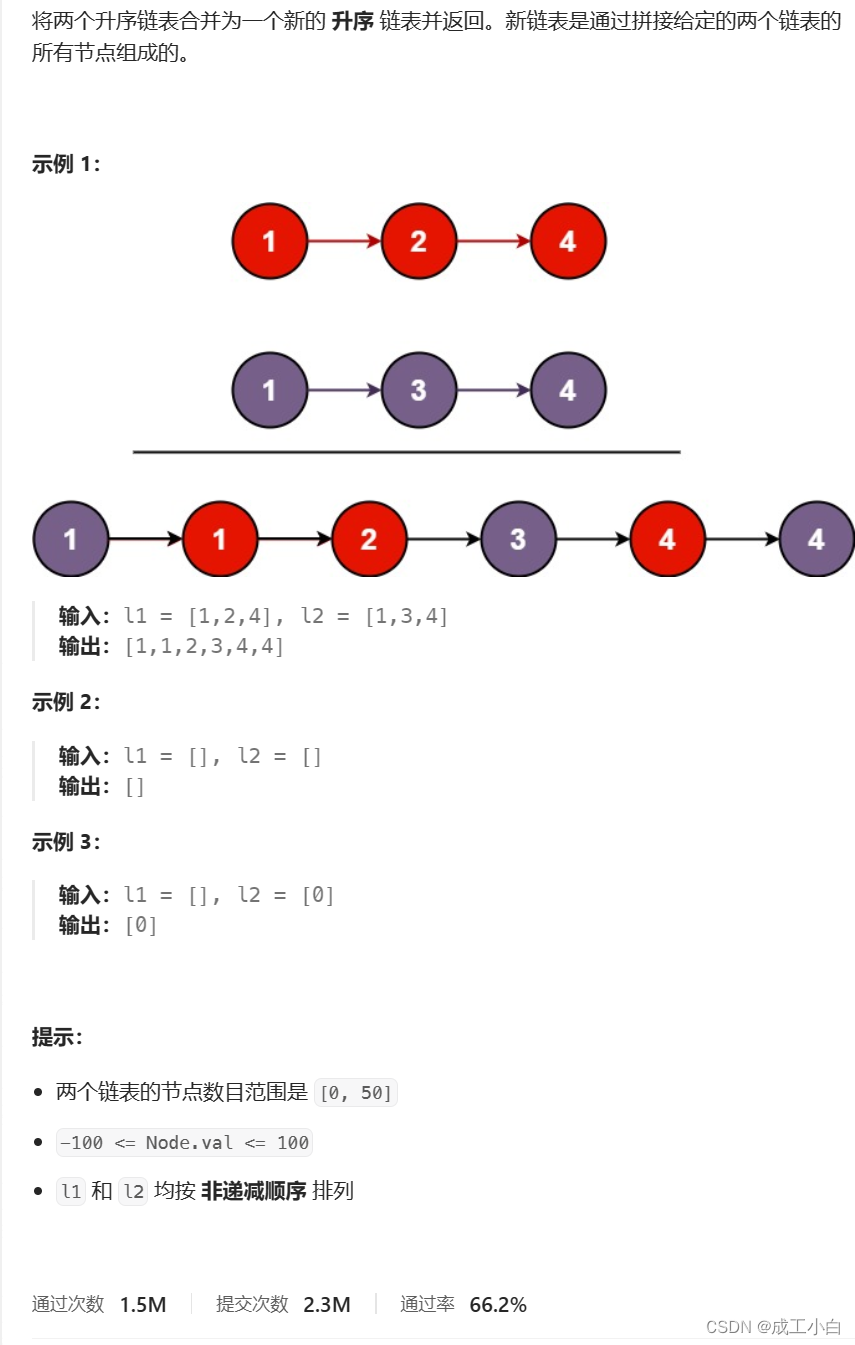
力扣练习——链表在线OJ
目录 提示: 一、移除链表元素 题目: 解答: 二、反转链表 题目: 解答: 三、找到链表的中间结点 题目: 解答: 四、合并两个有序链表(经典) 题目: 解…...
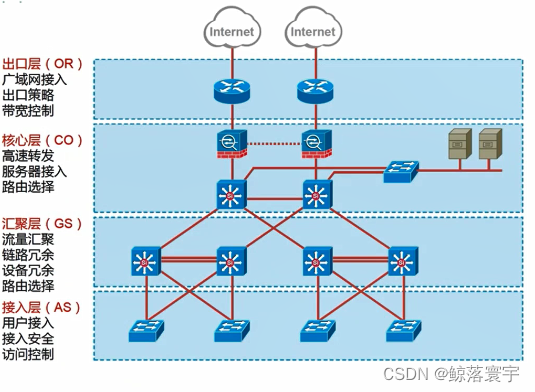
四、互联网技术——局域网拓扑结构
文章目录 一、局域网拓扑结构二、虚拟局域网VLAN三、交换机VLAN划分四、VLAN的作用五、交换机的端口类型六、经典三层网络架构七、例题:局域网带宽利用分析八、网络安全基础九、恶意软件十、防火墙与入侵检测技术 一、局域网拓扑结构 局域网的主要特征由网络的拓扑结构、所采用…...

Spring Webflux DispatcherHandler源码整理
DispatcherHandler的构造(以RequestMappingHandlerMapping为例) WebFluxAutoConfiguration中EnableWebFluxConfiguration继承WebFluxConfigurationSupportBean public DispatcherHandler webHandler() {return new DispatcherHandler(); }DispatcherHandler#setApplicationCon…...

【Netty】ByteToMessageDecoder源码解析
目录 1.协议说明 2.类的实现 3.Decoder工作流程 4.源码解析 4.1 ByteToMessageDecoder#channelRead 4.2 累加器Cumulator 4.3 解码过程 4.4 Decoder实现举例 5. 如何开发自己的Decoder 1.协议说明 Netty框架是基于Java NIO框架,性能彪悍,支持的协…...
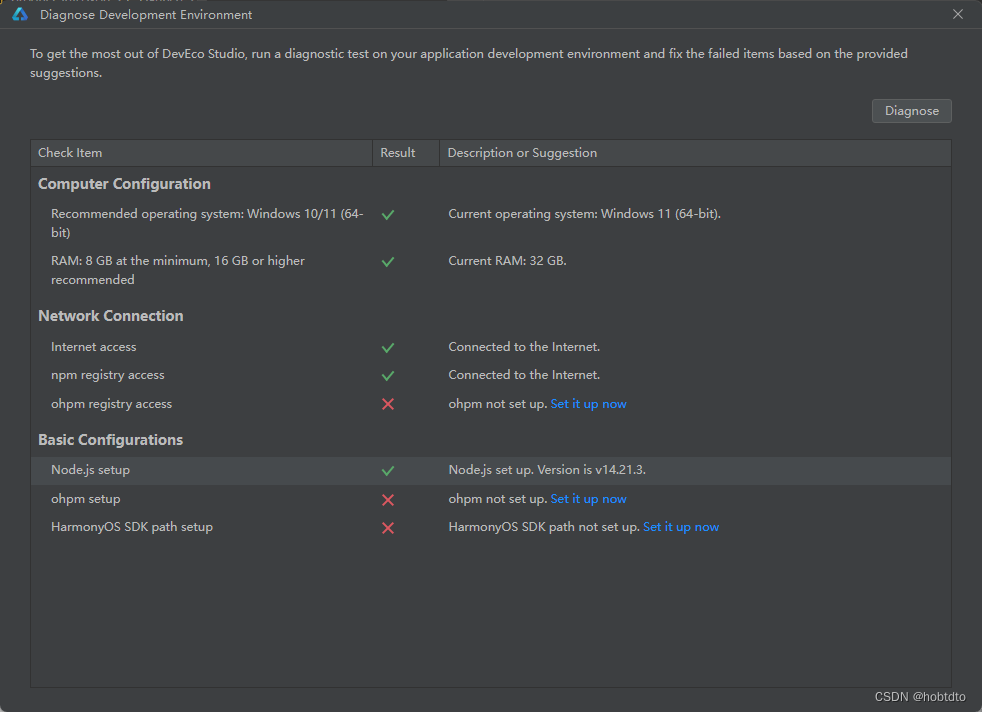
DevEco Studio设置Nodejs提示路径只能包含英文、数字、下划线等
安装DevEco Studio 3.1.1 Release 设置Nodejs路径使用nodejs默认安装路径 (C:\Program Files\nodejs) 提示只能包含英文、数字、下划线等 , 不想在安装nodejs请往下看 nodejs默认路径报错 修改配置文件 1、退出DevEco Studio 2、打开配置文件 cmd控制台…...
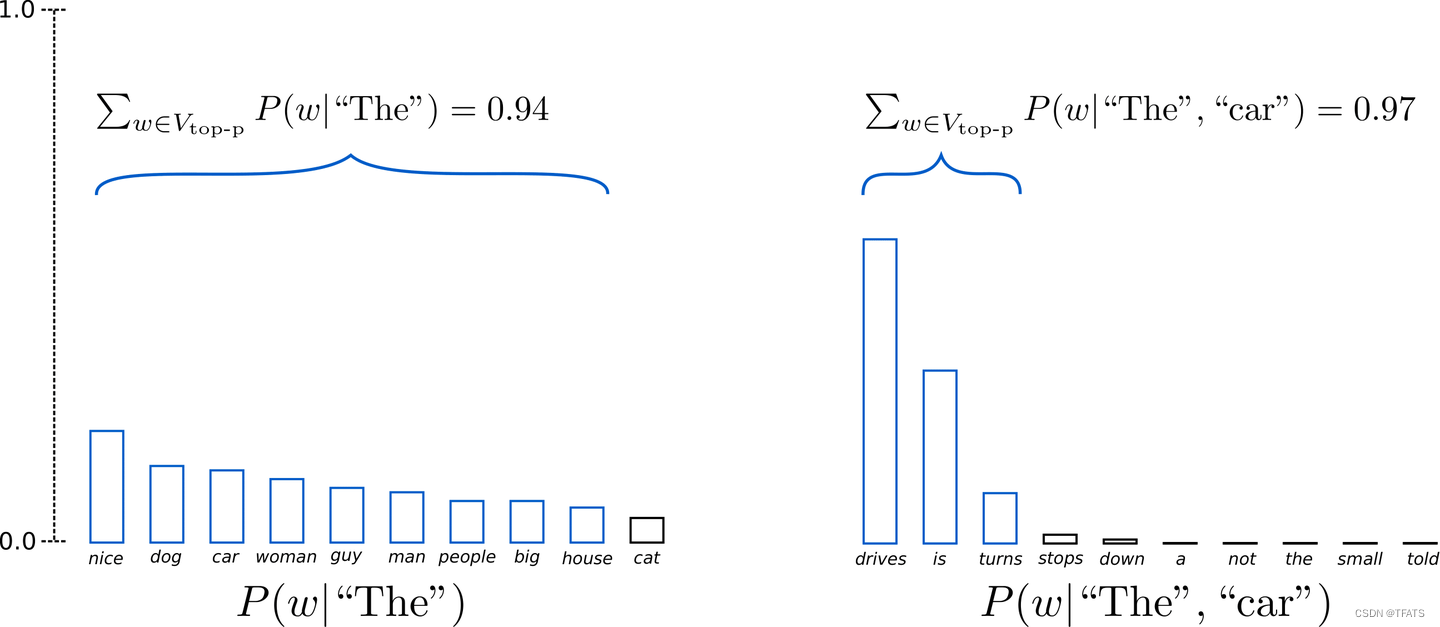
大模型 Decoder 的生成策略
本文将介绍以下内容: IntroductionGreedy Searchbeam searchSamplingTop-K SamplingTop-p (nucleus) sampling总结 一、Introduction 1、简介 近年来,由于在数百万个网页数据上训练的大型基于 Transformer 的语言模型的兴起,开放式语言生…...

队列和栈相互实现
相关题目 225. 用队列实现栈:弹出元素时,将对首的元素出列加到队尾,直到只剩下初始队列时队尾一个元素为止,然后弹出这个元素,即可实现LIFO 232. 用栈实现队列:用两个栈实现队列的功能,出栈时&a…...

Node.js 是如何处理请求的
前言:在服务器软件中,如何处理请求是非常核心的问题。不管是底层架构的设计、IO 模型的选择,还是上层的处理都会影响一个服务器的性能,本文介绍 Node.js 在这方面的内容。 TCP 协议的核心概念 要了解服务器的工作原理首先需要了…...
)
数据结构与算法之堆: Leetcode 215. 数组中的第K个最大元素 (Typescript版)
数组中的第K个最大元素 https://leetcode.cn/problems/kth-largest-element-in-an-array/ 描述 给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...
