数据结构与算法之堆: Leetcode 215. 数组中的第K个最大元素 (Typescript版)
数组中的第K个最大元素
- https://leetcode.cn/problems/kth-largest-element-in-an-array/
描述
- 给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
- 请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
- 你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
提示
- 1 <= k <= nums.length <= 1 0 5 10^5 105
- - 1 0 4 10^4 104 <= nums[i] <= 1 0 4 10^4 104
算法实现
1 )基于js中原生sort api
const findKthLargest = function(nums, k) {return nums.sort((a,b) => b-a)[k - 1]
};
- 这个浏览器默认提供的sort()方法,一般时间复杂度是 O(nlogn)
2 )基于堆的数据结构和堆排序的方法
// 建立最小堆类
class MinHeap {heap: number[] = [];// 交换节点位置swap(i, j) {[this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]];}// 获得父节点getParentIndex(i) {return (i - 1) >> 1;}// 获取左子节点getLeftIndex(i) {return (i << 1) + 1; // 极客写法}// 获取右子节点getRightIndex(i) {return (i << 1) + 2;}// 向上移动shiftUp(index) {// 如果到了堆顶元素,index是0,则不要再上移了if(!index) return;const parentIndex = this.getParentIndex(index)if(this.heap[parentIndex] > this.heap[index]) {this.swap(parentIndex, index)this.shiftUp(parentIndex)}}// 下移shiftDown(index) {// 边界1:如果到了堆尾元素,则不要再下移了if(index >= this.heap.length - 1) return;const size = this.size();const leftIndex = this.getLeftIndex(index);const rightIndex = this.getRightIndex(index);if (leftIndex < size && this.heap[leftIndex] < this.heap[index]) {this.swap(leftIndex, index);this.shiftDown(leftIndex);}if (rightIndex < size && this.heap[rightIndex] < this.heap[index]) {this.swap(rightIndex, index);this.shiftDown(rightIndex);}}// 插入insert(value) {this.heap.push(value);this.shiftUp(this.heap.length - 1);}// 删除堆顶pop() {// pop()方法删除数组最后一个元素并返回,赋值给堆顶this.heap[0] = this.heap.pop();// 对堆顶重新排序this.shiftDown(0);}// 获取堆顶peak() {return this.heap[0];}// 获取堆的大小size() {return this.heap.length;}
}// 实现
const findKthLargest = (nums, k) => {const h = new MinHeap();nums.forEach(n => {// 将数组元素依次插入堆中h.insert(n);// 如果堆满,则执行优胜劣汰(h.size() > k) && h.pop();})// 返回堆顶,此时就是第k大的元素return h.peak();
};
- 关键在于这个堆的数据结构提供的 insert 方法 与 pop 方法
- 时间复杂度:O(nlogk)
- 一个n循环,里面还嵌套一个heap的上移递归操作logk
- 总体:n*logk
- 空间复杂度: O(k) 或 O(logn)
- 堆的大小,数组的大小, k是输入的堆大小
- 注意
- 本题使用的是一个堆排序的算法,O(nlogn)
- 但是还有其他排序也可以达到这个效率
- 但是这个不符合题目的要求:时间复杂度为 O(n) 的算法
3 )基于快速排序
TODO
相关文章:
)
数据结构与算法之堆: Leetcode 215. 数组中的第K个最大元素 (Typescript版)
数组中的第K个最大元素 https://leetcode.cn/problems/kth-largest-element-in-an-array/ 描述 给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。…...
SpringBoot快速入门
搭建SpringBoot工程,定义hello方法,返回“Hello SpringBoot” ②导入springboot工程需要继承的父工程;以及web开发的起步依赖。 ③编写Controller ④引导类就是SpringBoot项目的一个入口。 写注解写main方法调用run方法 快速构建SpringBoo…...
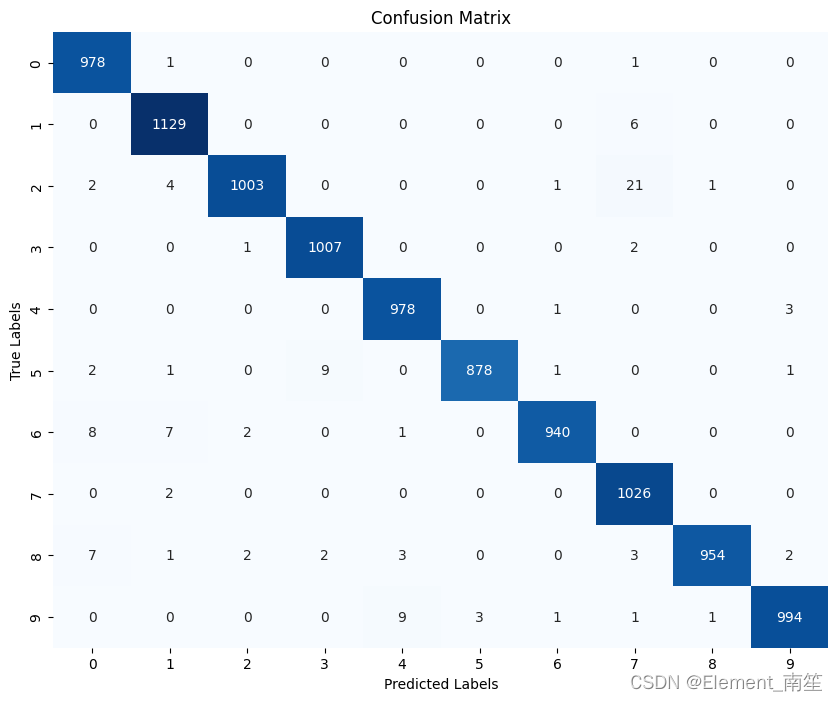
深度学习笔记_4、CNN卷积神经网络+全连接神经网络解决MNIST数据
1、首先,导入所需的库和模块,包括NumPy、PyTorch、MNIST数据集、数据处理工具、模型层、优化器、损失函数、混淆矩阵、绘图工具以及数据处理工具。 import numpy as np import torch from torchvision.datasets import mnist import torchvision.transf…...

高效的开发流程搭建
目录 1. 搭建 AI codebase 环境kaggle的服务器1. 搭建 AI codebase 环境 python 、torch 以及 cuda版本,对AI的影响最大。不同的版本,可能最终计算出的结果会有区别。 硬盘:PCIE转SSD的卡槽,, GPU: 软件源: Anaconda: 一定要放到固态硬盘上。 VS code 的 debug功能…...
浅谈OV SSL 证书的优势
随着网络威胁日益增多,保护网站和用户安全已成为每个企业和组织的重要任务。在众多SSL证书类型中,OV(Organization Validation)证书以其独特的优势备受关注。让我们深入探究OV证书的优势所在,为网站安全搭建坚实的防线…...

一篇博客学会系列(3) —— 对动态内存管理的深度讲解以及经典笔试题的深度解析
目录 动态内存管理 1、为什么存在动态内存管理 2、动态内存函数的介绍 2.1、malloc和free 2.2、calloc 2.3、realloc 3、常见的动态内存错误 3.1、对NULL指针的解引用操作 3.2、对动态开辟空间的越界访问 3.3、对非动态开辟内存使用free释放 3.4、使用free释放一块动态…...

【C++ techniques】虚化构造函数、虚化非成员函数
constructor的虚化 virtual function:完成“因类型而异”的行为;constructor:明确类型时构造函数;virtual constructor:视其获得的输入,可产生不同的类型对象。 //假如写一个软件,用来处理时事…...
11.6-LE Audio 笔记之初识音频位置和通道分配)
蓝牙核心规范(V5.4)11.6-LE Audio 笔记之初识音频位置和通道分配
专栏汇总网址:蓝牙篇之蓝牙核心规范学习笔记(V5.4)汇总_蓝牙核心规范中文版_心跳包的博客-CSDN博客 爬虫网站无德,任何非CSDN看到的这篇文章都是盗版网站,你也看不全。认准原始网址。!!! 音频位置 在以前的每个蓝牙音频规范中,只有一个蓝牙LE音频源和一个蓝牙LE音频接…...
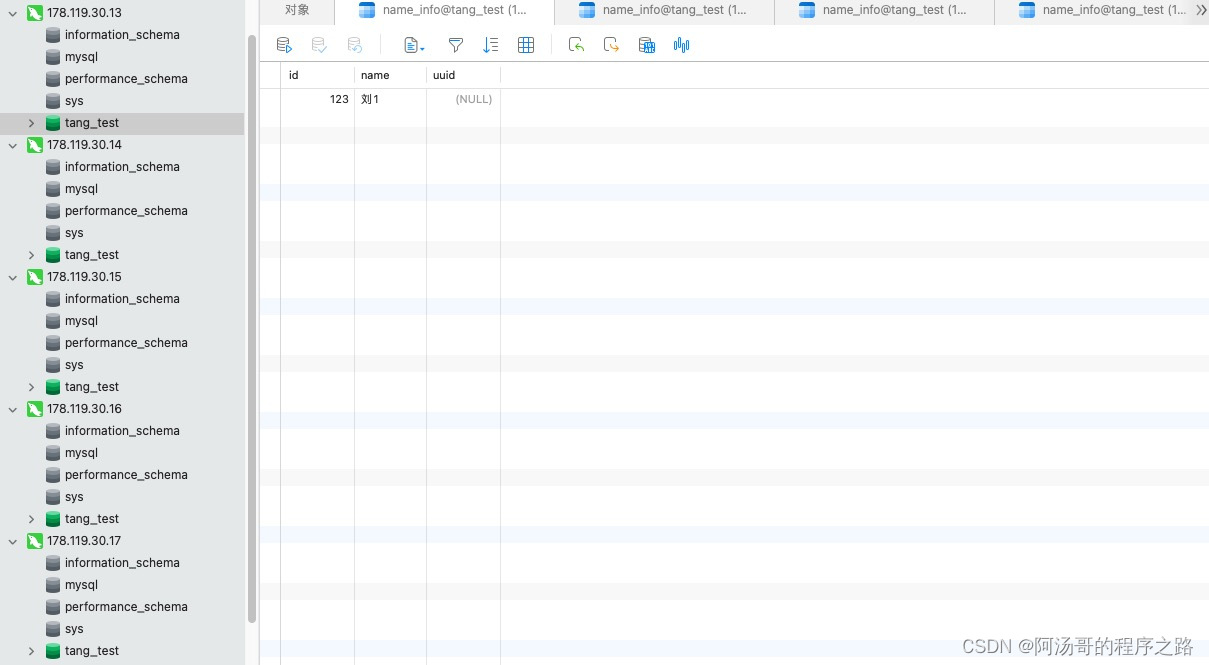
mysql双主+双从集群连接模式
架构图: 详细内容参考: 结果展示: 178.119.30.14(主) 178.119.30.15(主) 178.119.30.16(从) 178.119.30.17(从)...
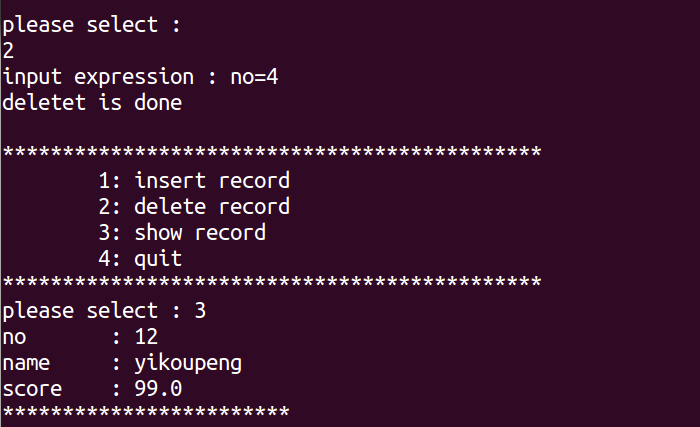
嵌入式中如何用C语言操作sqlite3(07)
sqlite3编程接口非常多,对于初学者来说,我们暂时只需要掌握常用的几个函数,其他函数自然就知道如何使用了。 数据库 本篇假设数据库为my.db,有数据表student。 nonamescore4嵌入式开发爱好者89.0 创建表格语句如下: CREATE T…...

RandomForestClassifier 与 GradientBoostingClassifier 的区别
RandomForestClassifier(随机森林分类器)和GradientBoostingClassifier(梯度提升分类器)是两种常用的集成学习方法,它们之间的区别分以下几点。 1、基础算法 RandomForestClassifier:随机森林分类器是基于…...
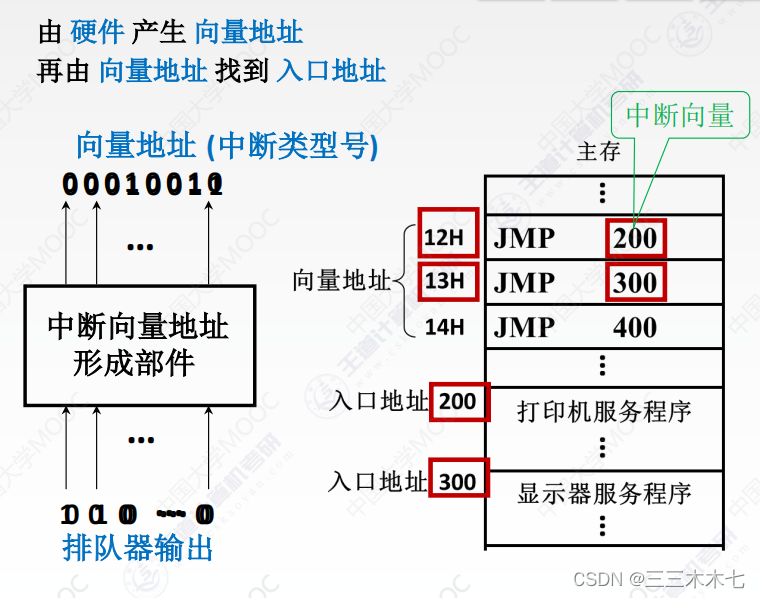
计组——I/O方式
一、程序查询方式 CPU不断轮询检查I/O控制器中“状态寄存器”,检测到状态为“已完成”之后,再从数据寄存器取出输入数据。 过程: 1.CPU执行初始化程序,并预置传送参数;设置计数器、设置数据首地址。 2. 向I/O接口发…...

jsbridge实战2:Swift和h5的jsbridge通信
[[toc]] demo1: 文本通信 h5 -> app 思路: h5 全局属性上挂一个变量app 接收这个变量的内容关键API: navigation代理 navigationAction.request.url?.absoluteString // 这个变量挂载在 request 的 url 上 ,在浏览器实际无法运行,因…...

集合原理简记
HashMap 无论在构造函数是否指定数组长度,进行的都是延迟初始化 构造函数作用: 阈值:threshold,每次<<1 ,数组长度 负载因子 无参构造:设置默认的负载因子 有参:可以指定初始容量或…...

机器学习的超参数 、训练集、归纳偏好
一、介绍 超参数(Hyperparameters)和验证集(Validation Set)是机器学习中重要的概念,用于调整模型和评估其性能。 超参数: 超参数是在机器学习模型训练过程中需要手动设置的参数,而不是从数据…...
Leetcode1071. 字符串的最大公因子(三种方法,带详细解析)
Leetcode1071. 字符串的最大公因子 对于字符串 s 和 t,只有在 s t … t(t 自身连接 1 次或多次)时,我们才认定 “t 能除尽 s”。 给定两个字符串 str1 和 str2 。返回 最长字符串 x,要求满足 x 能除尽 str1 且 x 能…...

如何像人类一样写HTML之图像标签,超链接标签与多媒体标签
文章目录 前言一、图像标签1.1 什么是图像标签?2.2 如何使用图像标签? 二、超链接标签2.1 什么是超链接标签?2.2 如何使用超链接标签? 三、多媒体标签3.1 什么是多媒体标签?3.2 如何使用多媒体audio标签?3.…...

1300*C. Rumor(并查集贪心)
解析: 并查集,求每个集合的最小费用。 每次合并集合的时候,根节点保存当前集合最小的费用。 #include<bits/stdc.h> using namespace std; #define int long long const int N1e55; int n,m,a[N],p[N],cnt[N]; int find(int x){retur…...
)
python实用小代码(数据分析向)
一、python实现31省市名称替换 首先定义了一个字典province_dict,其中包含每个省市的无缩写名称与其标准名称之间的映射。然后,我们使用map()函数将每个省市名称从无缩写名称转换为标准名称,并将结果存储在新列省市标准名称中。 province_di…...

【oncmdmsg 鼠标】2023/8/19 上午9:50:14
2023/8/19 上午9:50:14 oncmdmsg 鼠标 2023/8/19 上午9:50:22 抱歉,您提到的 “oncmdmsg” 和 “鼠标” 是什么?请提供更多上下文信息,我将尽力帮助您。 2023/8/19 上午9:51:43 OnCmdMsg 2023/8/19 上午9:52:21 “OnCmdMsg” 是一个在 MFC (Microsoft Foundation Cla…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
