浅谈OV SSL 证书的优势
随着网络威胁日益增多,保护网站和用户安全已成为每个企业和组织的重要任务。在众多SSL证书类型中,OV(Organization Validation)证书以其独特的优势备受关注。让我们深入探究OV证书的优势所在,为网站安全搭建坚实的防线。

首先,在验证机构身份方面,OV证书堪称金标准。OV证书不仅会对域名进行认证,还会认证企业或组织的真实性和合法性。验证过程涵盖了诸如公司名称、地址验证、电话核实等环节,确保证书持有者的身份可信且可追溯。这种严格的身份验证程序使得使用OV证书的网站更具权威性和可靠性,为用户提供了更高级别的信任感。

其次,安全浏览器界面的加密指示是OV证书的一大亮点。当用户访问一个有OV证书的网站时,浏览器地址栏通常显示一个带锁的图标和网站所有者的合法名称。这种明确而直观的显示方式,与扩展验证证书(EV证书)相近,增加了网站的可信度和专业形象。同时,它还提供了额外的安全保护,有效地防止钓鱼攻击和恶意网站冒充。
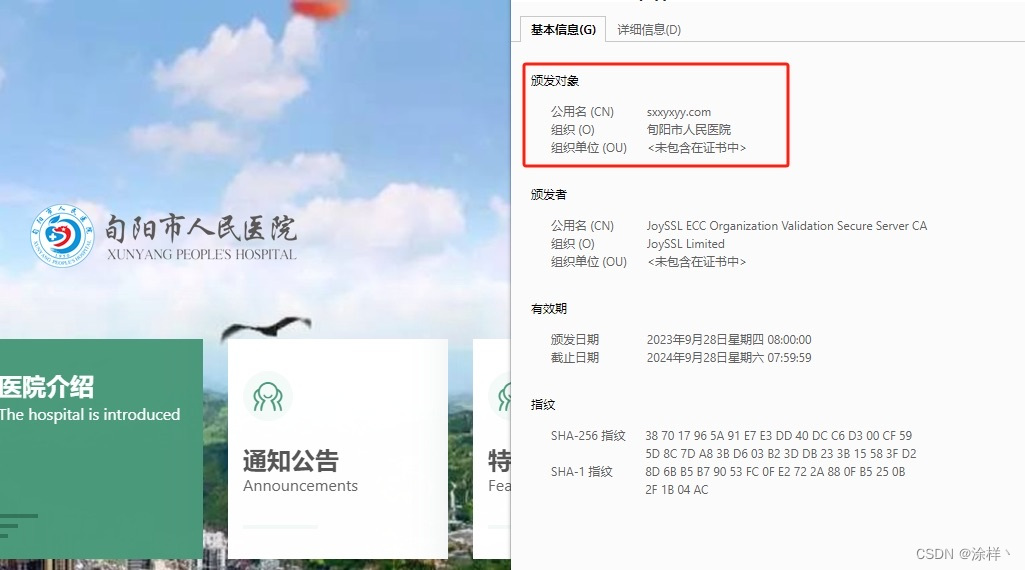
另外,OV证书还为网站提供了256位或更高等级加密,确保通过网站传输的数据得到强大的保护。这种高强度的数据加密能力可以有效防止信息被窃取、篡改或未经授权访问。无论是企业的机密文件、在线支付信息还是用户个人数据,OV证书都能为其提供可靠的保护屏障。
最后,OV证书还展示了企业的专业素质和合规性。在市场竞争激烈的今天,对于建立正面声誉和品牌形象至关重要。具备OV证书的网站显示出对信息安全的高度重视,向用户传递了一种负责任和值得信赖的形象。这有助于提升客户满意度和忠诚度,并促进更多交易的发生。
点击链接了解更多 OV 证书
总而言之,OV证书以其严格的身份验证、安全浏览器界面的加密指示、强大的数据保护和企业形象塑造方面的优势,成为保护网站和用户安全的理想选择。通过采用OV证书,网站可以强化自身的安全性和可信度,建立与用户之间的坚实信任基础。在数字时代,让我们共同致力于创建安全可靠的网络环境,为用户提供卓越的在线体验吧!
相关文章:

浅谈OV SSL 证书的优势
随着网络威胁日益增多,保护网站和用户安全已成为每个企业和组织的重要任务。在众多SSL证书类型中,OV(Organization Validation)证书以其独特的优势备受关注。让我们深入探究OV证书的优势所在,为网站安全搭建坚实的防线…...

一篇博客学会系列(3) —— 对动态内存管理的深度讲解以及经典笔试题的深度解析
目录 动态内存管理 1、为什么存在动态内存管理 2、动态内存函数的介绍 2.1、malloc和free 2.2、calloc 2.3、realloc 3、常见的动态内存错误 3.1、对NULL指针的解引用操作 3.2、对动态开辟空间的越界访问 3.3、对非动态开辟内存使用free释放 3.4、使用free释放一块动态…...

【C++ techniques】虚化构造函数、虚化非成员函数
constructor的虚化 virtual function:完成“因类型而异”的行为;constructor:明确类型时构造函数;virtual constructor:视其获得的输入,可产生不同的类型对象。 //假如写一个软件,用来处理时事…...
11.6-LE Audio 笔记之初识音频位置和通道分配)
蓝牙核心规范(V5.4)11.6-LE Audio 笔记之初识音频位置和通道分配
专栏汇总网址:蓝牙篇之蓝牙核心规范学习笔记(V5.4)汇总_蓝牙核心规范中文版_心跳包的博客-CSDN博客 爬虫网站无德,任何非CSDN看到的这篇文章都是盗版网站,你也看不全。认准原始网址。!!! 音频位置 在以前的每个蓝牙音频规范中,只有一个蓝牙LE音频源和一个蓝牙LE音频接…...
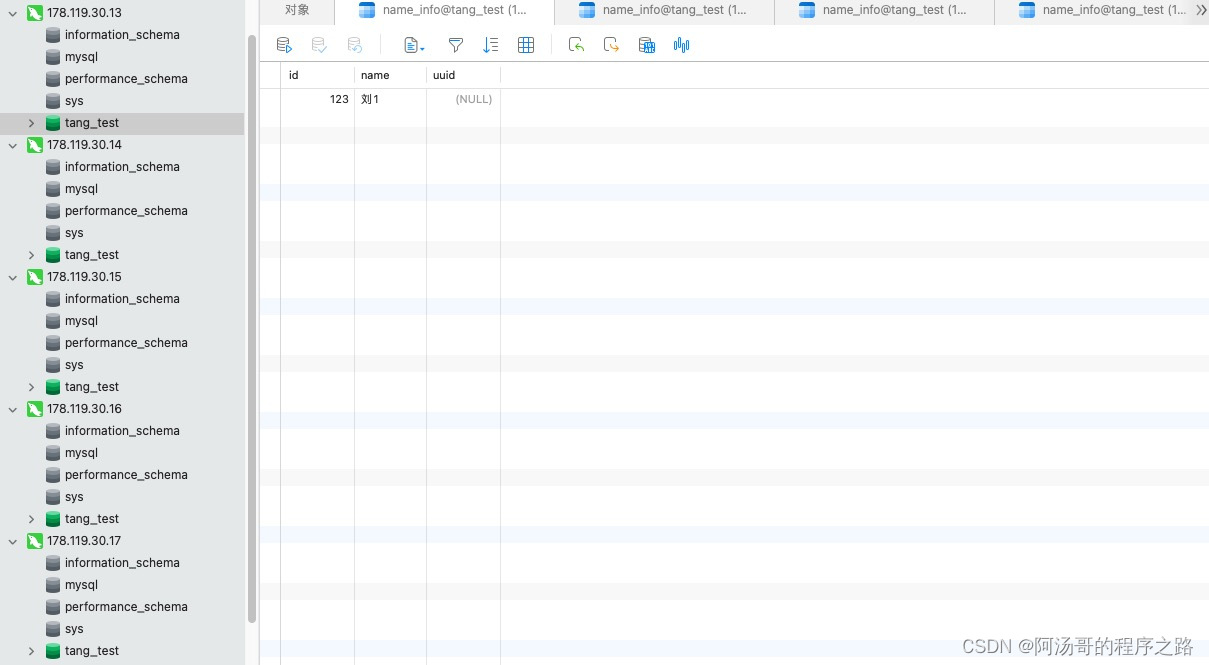
mysql双主+双从集群连接模式
架构图: 详细内容参考: 结果展示: 178.119.30.14(主) 178.119.30.15(主) 178.119.30.16(从) 178.119.30.17(从)...
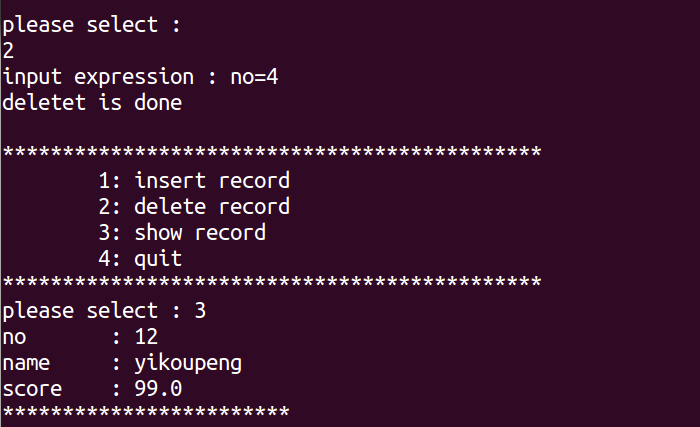
嵌入式中如何用C语言操作sqlite3(07)
sqlite3编程接口非常多,对于初学者来说,我们暂时只需要掌握常用的几个函数,其他函数自然就知道如何使用了。 数据库 本篇假设数据库为my.db,有数据表student。 nonamescore4嵌入式开发爱好者89.0 创建表格语句如下: CREATE T…...

RandomForestClassifier 与 GradientBoostingClassifier 的区别
RandomForestClassifier(随机森林分类器)和GradientBoostingClassifier(梯度提升分类器)是两种常用的集成学习方法,它们之间的区别分以下几点。 1、基础算法 RandomForestClassifier:随机森林分类器是基于…...
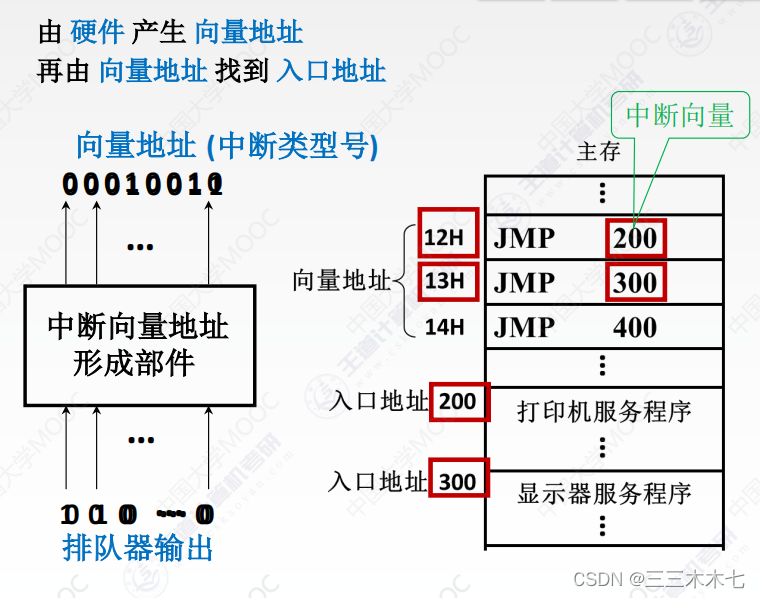
计组——I/O方式
一、程序查询方式 CPU不断轮询检查I/O控制器中“状态寄存器”,检测到状态为“已完成”之后,再从数据寄存器取出输入数据。 过程: 1.CPU执行初始化程序,并预置传送参数;设置计数器、设置数据首地址。 2. 向I/O接口发…...

jsbridge实战2:Swift和h5的jsbridge通信
[[toc]] demo1: 文本通信 h5 -> app 思路: h5 全局属性上挂一个变量app 接收这个变量的内容关键API: navigation代理 navigationAction.request.url?.absoluteString // 这个变量挂载在 request 的 url 上 ,在浏览器实际无法运行,因…...

集合原理简记
HashMap 无论在构造函数是否指定数组长度,进行的都是延迟初始化 构造函数作用: 阈值:threshold,每次<<1 ,数组长度 负载因子 无参构造:设置默认的负载因子 有参:可以指定初始容量或…...

机器学习的超参数 、训练集、归纳偏好
一、介绍 超参数(Hyperparameters)和验证集(Validation Set)是机器学习中重要的概念,用于调整模型和评估其性能。 超参数: 超参数是在机器学习模型训练过程中需要手动设置的参数,而不是从数据…...
Leetcode1071. 字符串的最大公因子(三种方法,带详细解析)
Leetcode1071. 字符串的最大公因子 对于字符串 s 和 t,只有在 s t … t(t 自身连接 1 次或多次)时,我们才认定 “t 能除尽 s”。 给定两个字符串 str1 和 str2 。返回 最长字符串 x,要求满足 x 能除尽 str1 且 x 能…...

如何像人类一样写HTML之图像标签,超链接标签与多媒体标签
文章目录 前言一、图像标签1.1 什么是图像标签?2.2 如何使用图像标签? 二、超链接标签2.1 什么是超链接标签?2.2 如何使用超链接标签? 三、多媒体标签3.1 什么是多媒体标签?3.2 如何使用多媒体audio标签?3.…...

1300*C. Rumor(并查集贪心)
解析: 并查集,求每个集合的最小费用。 每次合并集合的时候,根节点保存当前集合最小的费用。 #include<bits/stdc.h> using namespace std; #define int long long const int N1e55; int n,m,a[N],p[N],cnt[N]; int find(int x){retur…...
)
python实用小代码(数据分析向)
一、python实现31省市名称替换 首先定义了一个字典province_dict,其中包含每个省市的无缩写名称与其标准名称之间的映射。然后,我们使用map()函数将每个省市名称从无缩写名称转换为标准名称,并将结果存储在新列省市标准名称中。 province_di…...

【oncmdmsg 鼠标】2023/8/19 上午9:50:14
2023/8/19 上午9:50:14 oncmdmsg 鼠标 2023/8/19 上午9:50:22 抱歉,您提到的 “oncmdmsg” 和 “鼠标” 是什么?请提供更多上下文信息,我将尽力帮助您。 2023/8/19 上午9:51:43 OnCmdMsg 2023/8/19 上午9:52:21 “OnCmdMsg” 是一个在 MFC (Microsoft Foundation Cla…...

插入排序:简单而有效的排序方法
在计算机科学中,排序算法是一个重要且常见的主题,它们用于对数据进行有序排列。插入排序(Insertion Sort)是其中一个简单但有效的排序算法。本文将详细解释插入排序的原理和步骤,并提供Java语言的实现示例。 插入排序的…...

OpenGL之光照贴图
我们需要拓展之前的系统,引入漫反射和镜面光贴图(Map)。这允许我们对物体的漫反射分量和镜面光分量有着更精确的控制。 漫反射贴图 我们希望通过某种方式对物体的每个片段单独设置漫反射颜色。我们仅仅是对同样的原理使用了不同的名字:其实都是使用一张覆盖物体的图像,让我…...

隐私交易成新刚需,Unijoin 凭什么优势杀出重围?
随着区块链技术的普及和发展,全球加密货币用户在持续增长,根据火币研究院公布的数据,2022年全球加密用户已达到 3.2亿人,目前全球人口总数超过了 80亿,加密货币用户渗透率已达到了 4%。 尤其是在 2020 年开启的 DeFi 牛…...
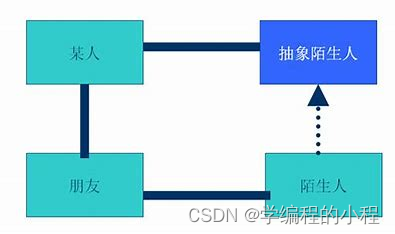
小谈设计模式(12)—迪米特法则
小谈设计模式(12)—迪米特法则 专栏介绍专栏地址专栏介绍 迪米特法则核心思想这里的“朋友”指当前对象本身以参数形式传入当前对象的对象当前对象的成员变量直接引用的对象目标 Java程序实现程序分析 总结 专栏介绍 专栏地址 link 专栏介绍 主要对目…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
