数组(数据结构)
优质博文:IT-BLOG-CN
一、简介
数组Array是一种线性表数据结构,它用一组连续的内存空间,存储一组具有相同类型的数据。

数组因具有连续的内存空间的特点,数据拥有非常高效率的“随机访问”,时间复杂度为O(1)。但因要保持这个连续的内存空间,导致数组在删除或插入操作的时非常低效。因为数组为了保持连续性,必然会涉及大量数据的迁移,这个是非常消耗时间的,平均时间复杂度为O(N)。
二、数组的随机访问
数组的随机访问是有个寻址公式的,上问中我们提到过数组是用一组连续的内存空间存储数据元素的,然而每个内存单元都有自己的地址(在计算机里面就是通过这个地址访问数据的),又加上每个内存单元的大小都是一样的,这样就很容易得到一个公式了,如下所示:
a[i]_address = base_address + i * data_type_size
我们来简单解释一下上述公式,其中data_type_size表示数组中每个元素的大小,base_address表示内存块的首地址,i表示数组下标。
三、数组的基本操作
【1】创建数组
public class MyArray { private int[] array; // 数组大小 private int size; public MyArray(int capacity) { this.size = 0; this.array = new int[capacity]; }
}
【2】读取元素: 我们知道数组在内存中是连续存储的,所以根据上文的寻址公式可以知道,我们可以根据数组下标i快速定位到对应的元素。
int[] array={1,2,3,4,5,6};
System.out.println(array[1]); // 输出的是2 因为数组的下标是从0开始的。
【3】更新元素: 我们可以根据数组下标快速查找到对应元素。那么同样道理,我们可以根据数组下标i快速更新元素,这中间涉及两个过程,首先就是找到数组下标i对应的数据元素A,然后将新的数据元素B赋值给A即完成更新。
int[] array={1,2,3,4,5,6};
System.out.println(array[1]); // 输出的是2
//更新数组下标为 1 的数组元素
array[1]=7;
System.out.println(array[1]); // 输出的是7
【3】插入元素:相比读取、更新操作,插入元素稍微复杂一些,分为以下两种情况:
尾部插入: 首先,我们看看尾部插入,这种情况很简单,在数组的最后新增一个新的元素,此时对于原数组来说没有任何影响,时间复杂度为0(1)。如下图所示:
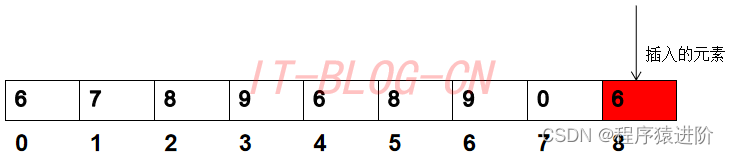
中间插入: 如果在数组的中间位置插入元素的话,此时会对插入元素位置之后的元素产生影响,也就是这些数据需要向后依次挪动一个位置。如下图所示:

/** * 插入元素* @param index 待插入的位置 * @param element 待插入的元素 */
public void insert(int index, int element){ if(index < 0 || index > size) { throw new IndexOutOfBoundsException("超过数组容量 ! 插入失败!"); } // 从左到右,将元素向右移动一位 for (int i = size-1; i > index; i--) {array[i+1] = array[i];} // 此时index这个位置已经腾空了,可以放进入element array[index]=element; //数组中元素个数+1 size++;
}
【4】删除元素: 删除元素和插入元素类似,如果我们删除第k个位置的数据,为了内存的连续性,同样会涉及数据的挪动。如下图所示:

/** * 根据数组下标删除元素* @param index 数组下标 * @return */
public int delete(int index) { if (index < 0 || index > size) { throw new IndexOutOfBoundsException("已经超过数组容量 ! 插入失败!"); } int deleteElement = array[index]; // 从左到右,将元素向左移动一位 for (int i = index; i < size - 1; i++) { array[i] = array[i + 1]; } size--; return deleteElement;
}
四、数组扩容
因为数组的长度在创建的时候已经确定了,当插入元素的时候如果数组已经满了,是没办法插入成功的。这个时候就要考虑数组扩容的问题了,那么该如何实现扩容呢?
其实我们可以这样,比如此时的数组是A, A已经满了,我们再创建一个数组B且数组长度是A的2倍,然后我们将数组A的元素全部放到数组B中,这样就完成了数组扩容了。
/** 数组扩容为原数组的二倍 **/
public void resize(){ int[] newArray = new int[array.length * 2]; System.arraycopy(array, 0, newArray, 0, array.length); // 把从索引0(第一个0)开始的array.length个数字复制到索引为0(第二个0)的位置上 array = newArray;
}
相关文章:

数组(数据结构)
优质博文:IT-BLOG-CN 一、简介 数组Array是一种线性表数据结构,它用一组连续的内存空间,存储一组具有相同类型的数据。 数组因具有连续的内存空间的特点,数据拥有非常高效率的“随机访问”,时间复杂度为O(1)。但因要保…...

C/C++ 二分查找面试算法题
1.二分查找(有序数组) https://blog.csdn.net/qq_63918780/article/details/122527681 1 #include <stdio.h>2 #include <string.h>3 4 int func(int *a,int j,int x)5 {6 int len j - 1,i 0,min;7 while(i<len)8 {9 …...

Linux基本指令(上)——“Linux”
各位CSDN的uu们好呀,今天,小雅兰的内容是Linux啦!!!主要是Linux的一些基本指令和Linux相关的基本概念(系统层面),下面,让我们进入Linux的世界吧!!…...
XSS详解
XSS一些学习记录 XXS短标签、属性、事件、方法短标签属性事件函数弹窗函数一些对于绕过有用的函数一些函数使用payload收集 浏览器编码问题XML实体编码URL编码JS编码混合编码 一些绕过方法利用constructor原型污染链构造弹框空格绕过圆括号过滤绕过其他的一些绕过 参考 XXS短标…...

【图论】判环问题
(未更新完、做到相关题再更新相关部分 文章目录 无向图判断有无环并输出环上点 无向图判断有无环并输出环上点 例题:H. Mad City 利用变种拓扑排序,先把度为1的点存入队中,每次取出队头,遍历邻接点,再将该…...

将3D MAX设计模型导入NX1988
将3D MAX设计模型导入NX1988 概述导入流程导出喜欢的模型对模型进行修改模型贴图 概述 一般家装设计都不会用NX之类的产品设计软件,也没有通用的文件格式可以互相转换,本文的目的是将从网上下载的一些设计较好的3D MAX模型导入到NX软件中借用࿰…...

操作系统原理实验三:页面调度算法程序
实验三:页面调度算法程序 课程名称:操作系统原理 项目名称:页面调度算法程序 实验(实训)类型:验证性实验 实验(实训)课时:2 [目的和要求] 目的: 加深对请…...
QT实现tcp服务器客户端
服务器.cpp #include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);//实例化一个服务器server new QTcpServer(this);// 此时,服务器已经成功进入监听状态…...

tcp拥塞控制原理
18.3 拥塞控制 我们在向对端发送数据时,并不是一股脑子任意发送,因为TCP建立连接后,就是建立了一根管道,这跟管道上,实际上有很多的工作设备,比如路由器和交换机等等,他们都会对接收到的TCP包进…...

【C++设计模式之简单工厂模式】分析及示例
简介 简单工厂模式是一种常见的设计模式,用于创建多种相似对象的实例,属于创建型。 它通过一个工厂类来解耦客户端代码和对象的创建过程,使得客户端无需直接和具体的产品类交互,而只需要通过工厂类获取所需的产品实例即可。 原理…...

云原生定义整理
云原生定义整理 Pivotal 是云原生应用的提出者,并推出了 Pivotal Cloud Foundry 云原生应用平台和 Spring 开源 Java 开发框架,成为云原生应用架构中先驱者和探路者。 Pivotal最初的定义 Pivotal公司的Matt Stine在2015年写了一本叫做<<迁移到云…...
华硕X555YI, Win11下无法调节屏幕亮度
翻出一个旧电脑华硕X555YI,装Win11玩,已经估计到会有一些问题。 果然,装完之后,发现屏幕无法调节亮度。试了网上的一些方法,比如修改注册表等,无效。 估计是显卡比较老,哪里没兼容。然后用驱动…...

踩坑 | vue动态绑定img标签src属性的一系列报错
文章目录 踩坑 | vue项目运行后使用require()图片也不显示问题描述vue中动态设置img的src不生效问题的原因require is not defined 解决办法1:src属性直接传入地址解决办法2 踩坑 | vue项目运行后使用require()图片也不显示 问题描述 在网上查阅之后,发…...

强化学习环境 - robogym - 学习 - 1
强化学习环境 - robogym - 学习 - 1 项目地址 https://github.com/openai/robogym 为什么选择 robogym 自己的项目需要做一些机械臂 table-top 级的多任务操作 robogym 基于 mujoco 搭建,构建了一个仿真机械臂桌面物体操作(pick-place、stack、rearr…...

如果在 Mac 上的 Safari 浏览器中无法打开网站
使用网络管理员提供的信息更改代理设置。个人建议DNS解析,设置多个例如114.114.114.114 8.8.8.8 8.8.4.4 如果打不开网站,请尝试这些建议。 在 Mac 上的 Safari 浏览器 App 中,检查页面无法打开时出现的信息。 这可能会建议解决问题的…...
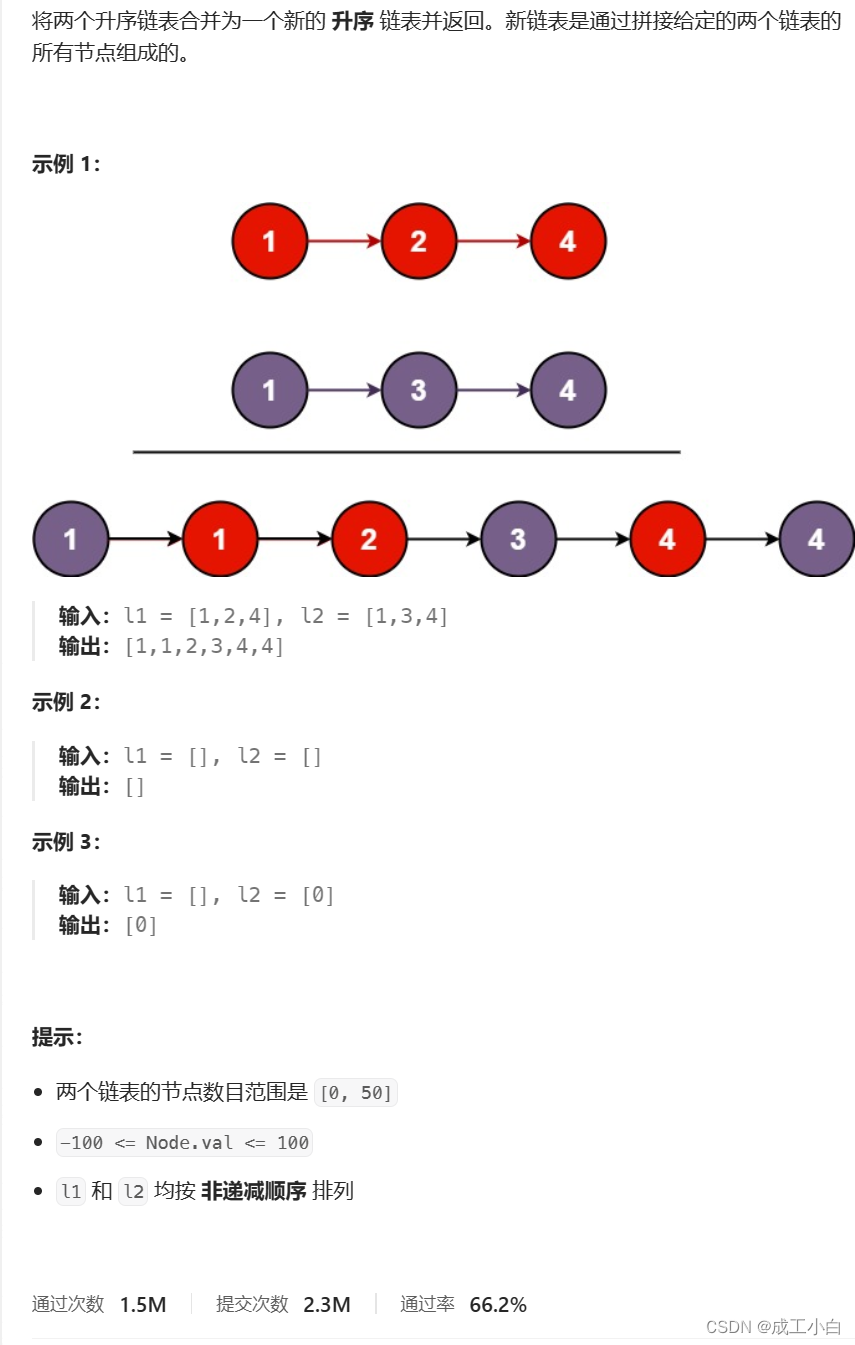
力扣练习——链表在线OJ
目录 提示: 一、移除链表元素 题目: 解答: 二、反转链表 题目: 解答: 三、找到链表的中间结点 题目: 解答: 四、合并两个有序链表(经典) 题目: 解…...
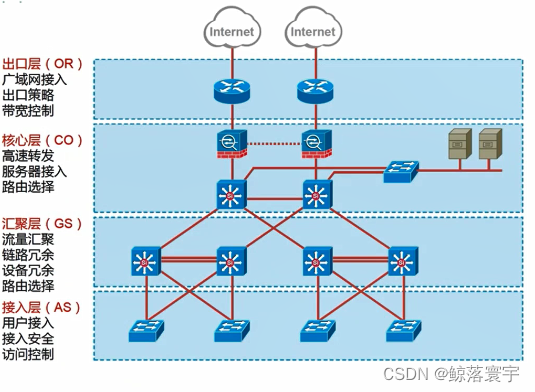
四、互联网技术——局域网拓扑结构
文章目录 一、局域网拓扑结构二、虚拟局域网VLAN三、交换机VLAN划分四、VLAN的作用五、交换机的端口类型六、经典三层网络架构七、例题:局域网带宽利用分析八、网络安全基础九、恶意软件十、防火墙与入侵检测技术 一、局域网拓扑结构 局域网的主要特征由网络的拓扑结构、所采用…...

Spring Webflux DispatcherHandler源码整理
DispatcherHandler的构造(以RequestMappingHandlerMapping为例) WebFluxAutoConfiguration中EnableWebFluxConfiguration继承WebFluxConfigurationSupportBean public DispatcherHandler webHandler() {return new DispatcherHandler(); }DispatcherHandler#setApplicationCon…...

【Netty】ByteToMessageDecoder源码解析
目录 1.协议说明 2.类的实现 3.Decoder工作流程 4.源码解析 4.1 ByteToMessageDecoder#channelRead 4.2 累加器Cumulator 4.3 解码过程 4.4 Decoder实现举例 5. 如何开发自己的Decoder 1.协议说明 Netty框架是基于Java NIO框架,性能彪悍,支持的协…...
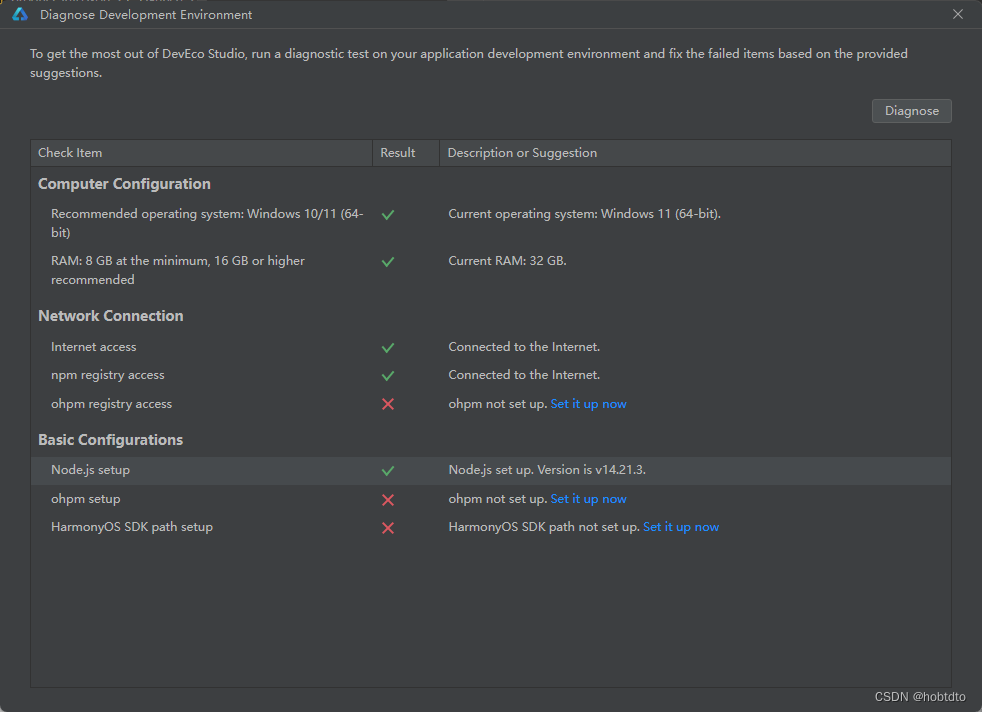
DevEco Studio设置Nodejs提示路径只能包含英文、数字、下划线等
安装DevEco Studio 3.1.1 Release 设置Nodejs路径使用nodejs默认安装路径 (C:\Program Files\nodejs) 提示只能包含英文、数字、下划线等 , 不想在安装nodejs请往下看 nodejs默认路径报错 修改配置文件 1、退出DevEco Studio 2、打开配置文件 cmd控制台…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
