面试常用排序查找算法
文章目录
- 1 二分查找
- 2 冒泡排序
- 3 堆排序
- 4 插入排序
- 5 快速排序
- 6 选择排序
- 7 希尔排序
1 二分查找
- 定义两个变量
left和right,分别表示数组的左边界和右边界,初始值分别为0和len - 1,其中len是数组的长度。 - 计算数组的中间位置
mid,公式为(left + right) / 2,并判断数组中该位置的元素num[mid]是否等于目标值target。 - 如果相等,说明找到了目标值,返回
mid作为结果。 - 如果不相等,比较
num[mid]和target的大小,如果num[mid] < target,说明目标值在数组的右半部分,因此将左边界更新为mid + 1;如果num[mid] > target,说明目标值在数组的左半部分,因此将右边界更新为mid - 1。 - 重复步骤2到4,直到左边界大于右边界,这时说明数组中不存在目标值,返回-1作为结果。
二分查找算法的优点是查找速度快,时间复杂度为 O ( l o g n ) O(logn) O(logn),其中n是数组的长度。缺点是要求数组必须是有序的,并且对于动态变化的数组不适用。
int BinarySearch(int num[],int target,int len)
{int left = 0, right = len - 1;while(left <= right){int mid = (left + right) / 2;if(num[mid]==target){return mid;}else if(num[mid] < target){left = mid + 1;}else{right = mid - 1;}}return -1;
}
2 冒泡排序
- 定义一个变量
i,表示数组中未排序的部分的最后一个元素的位置,初始值为length - 1,其中length是数组的长度。 - 从数组的第一个元素开始,依次比较相邻的两个元素,如果前一个元素
num[j]大于后一个元素num[j+1],则交换它们的位置,这样可以将较大的元素向后移动。 - 重复步骤2,直到遍历到数组中未排序部分的最后一个元素,这时可以确定该元素是数组中最大的元素,并将其排在正确的位置。
- 将变量
i减一,表示数组中未排序部分的长度减少了一个元素,然后回到步骤2,继续进行比较和交换。 - 重复步骤2到4,直到变量
i小于等于1,这时说明数组中所有的元素都已经排好序,算法结束。
冒泡排序算法的优点是简单易懂,不需要额外的空间。缺点是效率低,时间复杂度为 O ( n 2 ) O(n^2) O(n2),其中n是数组的长度。
void BubbleSort(int num[],int length)
{for(int i=length-1;i>1;i--){for(int j=0;j<i;j++){if(num[j] > num[j+1]){int tmp = num[j+1];num[j+1] = num[j];num[j] = tmp;}}}
}
3 堆排序
- 定义一个函数
MaxHeap,它的作用是将一个数组中的一部分元素调整为一个大根堆,即满足父节点的值大于等于子节点的值的二叉树。函数的参数有三个,分别是num表示数组,start表示调整的起始位置,end表示调整的结束位置。 - 在函数
MaxHeap中,定义两个变量dad和son,分别表示当前要调整的父节点和子节点的位置,初始值分别为start和start * 2 + 1(因为数组下标从0开始,所以左子节点是父节点乘以2再加1)。 - 判断子节点是否在调整范围内,如果是,则继续执行以下步骤;如果不是,则说明已经调整完毕,返回。
- 如果存在右子节点,并且右子节点的值大于左子节点的值,则将子节点更新为右子节点(即选择较大的子节点)。
- 比较父节点和子节点的值,如果父节点的值大于等于子节点的值,则说明已经满足大根堆的性质,返回;如果不是,则交换父节点和子节点的值,并将父节点更新为原来的子节点,子节点更新为原来父节点的左子节点(即向下一层继续调整)。
- 重复步骤3到5,直到调整完毕或者返回。
- 定义一个函数
HeapSort,它的作用是对一个数组进行堆排序。函数的参数有两个,分别是num表示数组,len表示数组的长度。 - 从数组中间位置开始,依次对每个元素执行函数
MaxHeap,这样可以将整个数组调整为一个大根堆(即第一个元素是最大的元素)。 - 从数组最后一个元素开始,依次执行以下步骤:
- 交换第一个元素和当前元素的值,这样可以将最大的元素放在正确的位置。
- 对除了当前元素之外的其他元素执行函数
MaxHeap,这样可以将剩余部分重新调整为一个大根堆(即第一个元素是剩余部分最大的元素)。
- 重复步骤9,直到只剩下第一个元素,这时说明数组中所有的元素都已经排好序,算法结束。
堆排序算法的优点是效率高,时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn),其中n是数组的长度。缺点是需要额外的空间来存储堆结构,并且对于稳定性要求高的场合不适用。
void MaxHeap(int num[],int start,int end)
{int dad = start;int son = dad * 2 + 1;while(son <=end){if((son+1<=end) && (num[son]<num[son+1])){son++;}if(num[son]<num[dad]){return;}else{int tmp = num[dad];num[dad] = num[son];num[son] = tmp;dad = son;son = dad * 2 + 1;}}
}void HeapSort(int num[],int len)
{for(int i=len/2-1;i>=0;i--){MaxHeap(num,i,len-1);}for(int i=len-1;i>0;i--){int tmp = num[0];num[0] = num[i];num[i] = tmp;MaxHeap(num,0,i-1);}
}
4 插入排序
- 定义一个变量
i,表示当前要插入的元素的位置,初始值为1,表示从数组的第二个元素开始。 - 将当前要插入的元素
num[i]保存在一个临时变量tmp中,以免被覆盖。 - 定义一个变量
j,表示已经排好序的部分的最后一个元素的位置,初始值为i - 1。 - 比较已经排好序的部分的最后一个元素
num[j]和要插入的元素tmp的大小,如果前者大于后者,则将前者向后移动一位,即将num[j]赋值给num[j+1],并将j减一;如果不是,则说明找到了要插入的位置,跳出循环。 - 将要插入的元素
tmp赋值给找到的位置,即将tmp赋值给num[j+1]。 - 将变量
i加一,表示要插入下一个元素,并回到步骤2,继续进行比较和移动。 - 重复步骤2到6,直到变量
i等于数组的长度,这时说明数组中所有的元素都已经排好序,算法结束。
插入排序算法的优点是简单易懂,对于部分有序或者数据量较小的数组效率较高。缺点是效率低,时间复杂度为 O ( n 2 ) O(n^2) O(n2),其中n是数组的长度。
void InsertSort(int num[],int length)
{for(int i=1;i<length;i++){int tmp = num[i];int j = i - 1;while((j>=0) && (num[j]>tmp)){num[j+1] = num[j];j--;}num[j+1] = tmp;}
}
5 快速排序
- 定义一个函数
QuickSort,它的作用是对一个数组的一部分进行快速排序。函数的参数有三个,分别是num表示数组,start表示排序的起始位置,end表示排序的结束位置。 - 判断是否需要排序,如果起始位置大于等于结束位置,则说明已经排好序,返回;如果不是,则继续执行以下步骤。
- 定义两个变量
i和j,分别表示当前要划分的部分的左边界和右边界,初始值分别为start和end。 - 选择数组中第一个元素
num[i]作为基准值,并将其保存在一个临时变量basenum中,以免被覆盖。 - 从右边界开始,向左寻找一个小于基准值的元素,如果找到,则将其赋值给左边界位置;如果没有找到,则将右边界减一,继续寻找。
- 从左边界开始,向右寻找一个大于基准值的元素,如果找到,则将其赋值给右边界位置;如果没有找到,则将左边界加一,继续寻找。
- 重复步骤5和6,直到左边界和右边界相遇或者交叉,这时说明已经完成了一次划分,并将基准值赋值给相遇或者交叉的位置。
- 对基准值左边的部分递归地执行函数
QuickSort,对基准值右边的部分递归地执行函数QuickSort。 - 重复步骤2到8,直到所有的部分都排好序,算法结束。
快速排序算法的优点是效率高,时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn),其中n是数组的长度。缺点是不稳定,并且对于极端情况(如数组已经有序或者逆序)效率低。
void QuickSort(int num[],int start,int end)
{if(start >= end) return;int i = start;int j = end;int basenum = num[i];while(i<j){//从右往左找小值while((i<j) && (num[j]>=basenum)){j--;}if(i<j){num[i] = num[j];i++;}//从左往右找大值while((i<j) && (num[i]<basenum)){i++;}if(i<j){num[j] = num[i];j--;}num[i] = basenum;}QuickSort(num,start,i-1);QuickSort(num,i+1,end);
}
6 选择排序
- 定义一个变量
i,表示当前要选择的位置,初始值为0,表示从数组的第一个元素开始。 - 定义一个变量
min,表示当前最小元素的位置,初始值为i。 - 从当前位置开始,向后遍历数组中的每个元素,如果发现有比当前最小元素更小的元素,则将其位置赋值给
min,这样可以找到当前范围内最小的元素。 - 交换当前位置和最小元素的值,即将
num[min]赋值给num[i],将num[i]赋值给num[min],这样可以将最小的元素放在正确的位置。 - 将变量
i加一,表示要选择下一个位置,并回到步骤2,继续进行选择和交换。 - 重复步骤2到5,直到变量
i等于数组的长度减一,这时说明数组中所有的元素都已经排好序,算法结束。
选择排序算法的优点是简单易懂,不需要额外的空间。缺点是效率低,时间复杂度为 O ( n 2 ) O(n^2) O(n2),其中n是数组的长度。
void SelectSort(int num[],int length)
{for(int i=0;i<length-1;i++){int min = i;for(int j=i;j<length;j++){if(num[j]<num[min]){min = j;}}int tmp = num[min];num[min] = num[i];num[i] = tmp;}
}
7 希尔排序
- 定义一个变量
gap,表示当前要排序的元素的间隔,初始值为数组的长度length。 - 计算新的间隔,公式为
gap = gap / 3 + 1,这样可以逐渐减小间隔,直到为1。 - 对每个间隔进行以下步骤:
- 定义一个变量
i,表示当前要排序的间隔的起始位置,初始值为0。 - 从当前位置开始,向后遍历数组中的每个间隔内的元素,如果发现有比前一个间隔内的元素更小的元素,则将其保存在一个临时变量tmp中,并执行以下步骤:
- 定义一个变量
k,表示已经排好序的部分的最后一个间隔内的元素的位置,初始值为当前位置减去间隔,即k = j - gap。 - 比较已经排好序的部分的最后一个间隔内的元素
num[k]和要插入的元素tmp的大小,如果前者大于后者,则将前者向后移动一个间隔,即将num[k]赋值给num[k+gap],并将k减去间隔,继续比较;如果不是,则说明找到了要插入的位置,跳出循环。 - 将要插入的元素
tmp赋值给找到的位置,即将tmp赋值给num[k+gap]。
- 定义一个变量
- 将变量
i加一,表示要排序下一个间隔,并回到步骤3.2,继续进行遍历和插入。
- 定义一个变量
- 重复步骤2和3,直到变量
gap等于1,这时说明数组中所有的元素都已经排好序,算法结束。
希尔排序算法的优点是效率高于简单插入排序,时间复杂度为 O ( n 1.3 ) O(n^{1.3}) O(n1.3),其中n是数组的长度。缺点是不稳定,并且对于不同的间隔选择效率有影响。
void ShellSort(int num[],int length)
{int gap = length;do{gap = gap / 3 + 1;for(int i=0;i<gap;i++){for(int j=gap+i;j<length;j+=gap){if(num[j] < num[j-gap]){int tmp = num[j];int k;for(k=j-gap;(k>=0) && (num[k]>tmp);k-=gap){num[k+gap] = num[k];}num[k+gap] = tmp;}}}} while(gap>1);
}
相关文章:

面试常用排序查找算法
文章目录 1 二分查找2 冒泡排序3 堆排序4 插入排序5 快速排序6 选择排序7 希尔排序 1 二分查找 定义两个变量left和right,分别表示数组的左边界和右边界,初始值分别为0和len - 1,其中len是数组的长度。计算数组的中间位置mid,公式…...

CUDA C编程权威指南:1.1-CUDA基础知识点梳理
主要整理了N多年前(2013年)学习CUDA的时候开始总结的知识点,好长时间不写CUDA代码了,现在LLM推理需要重新学习CUDA编程,看来出来混迟早要还的。 1.CUDA 解析:2007年,NVIDIA推出CUDA(…...

讲讲项目里的仪表盘编辑器(四)分页卡和布局容器组件
讲讲两个经典布局组件的实现 ① 布局容器组件 配置面板是给用户配置布局容器背景颜色等属性。这里我们不需要关注 定义文件 规定了组件类的类型、标签、图标、默认布局属性、主文件等等。 // index.js import Container from ./container.vue; class ContainerControl extends…...

Qt模块、Qt开发应用程序类型、Qt未来主要市场、Qt6功能普及
Qt模块、Qt开发应用程序类型、Qt未来主要市场、Qt6功能普及 文章目录 1.Qt核心模块2.Qt的功能拓展3.Qt未来主要市场4.Qt6功能普及5.弃用的功能: Qt是一个跨平台的应用程序开发框架,提供了丰富的模块和工具来开发各种类型的应用程序。以下是Qt目前已有的…...

nodejs+vue高校校图书馆elementui
管理员输入书籍所在的书架位置,借阅提醒系统:可以查看个人借阅信息和图书到期提醒、挂失、检索、虚拟借书证不仅为群众提供了服务,而且也推广了自己,让更多的群众了解自己。 管理员页面: 第三章 系统分析 10 3.1需求分…...

CUDA C编程权威指南:1.2-CUDA基础知识点梳理
主要整理了N多年前(2013年)学习CUDA的时候开始总结的知识点,好长时间不写CUDA代码了,现在LLM推理需要重新学习CUDA编程,看来出来混迟早要还的。 1.闭扫描和开扫描 对于一个二元运算符 ⊕ \oplus ⊕和一个 n n n元…...

C语言—位运算符
目录 &(位与,AND): |(位或,OR): 位取反(~): 左移(<<): 右移(>>): &(位与,AND)&…...

怎么才能实现一个链接自动识别安卓.apk苹果.ipa手机和win电脑wac电脑
您想要实现的功能是通过检测用户代理(User Agent)来识别访问设备类型并根据设备类型展示相应的页面。您可以根据以下步骤进行实现: 选择后端语言和框架,例如:Node.js、Express。 创建一个新的Express项目。 编写一个…...
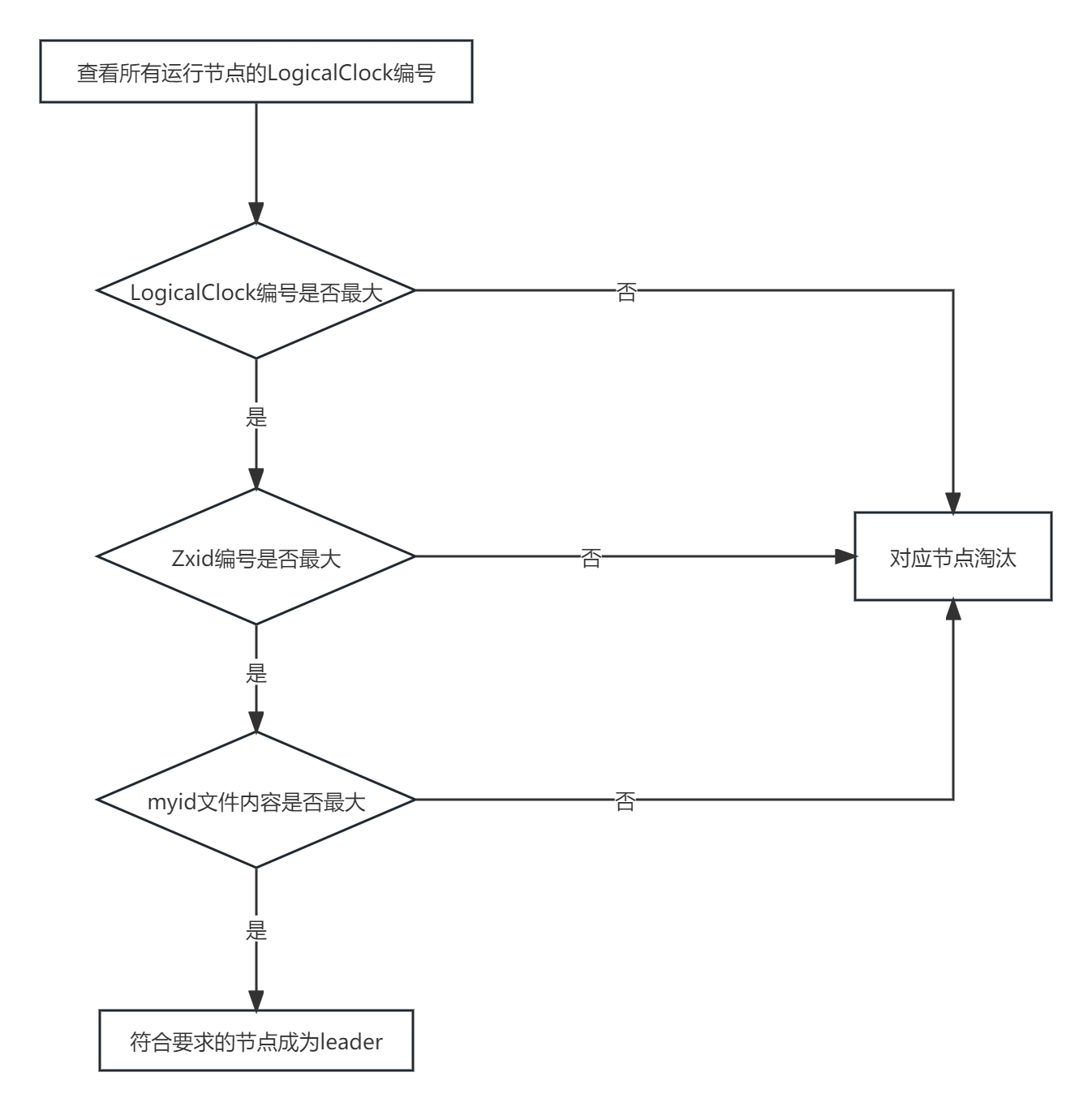
zookeeper选举机制
全新集群选举 zookeeper 全新集群选举机制网上资料很多说法很模糊,仔细思考了一下,应该是这样 得到票数最多的机器>机器总数半数 具体启动过程中的哪个节点成为 leader 与 zoo.cfg 中配置的节点数有关,下面以3个举例 选举过程如下 server…...

vcpkg切换 Visual Studio 版本
vcpkg切换 Visual Studio 版本 在使用vcpkg作为项目的包管理工具时,可能会遇到需要切换Visual Studio版本的情况。下面是一种简单的方法来实现这个目标,通过修改triplet文件来指定使用的Visual Studio版本。 步骤1: 创建或修改Triplet文件 首先&#…...
运算符重载
#include <iostream> using namespace std; class Num { private:int num1; //实部int num2; //虚部 public:Num(){}; //无参构造Num(int n1,int n2):num1(n1),num2(n2){}; //有参构造~Num(){}; //析构函数const Num operator(const Num &other)const //加号重载{Nu…...

Llama2-Chinese项目:7-外延能力LangChain集成
本文介绍了Llama2模型集成LangChain框架的具体实现,这样可更方便地基于Llama2开发文档检索、问答机器人和智能体应用等。 1.调用Llama2类 针对LangChain[1]框架封装的Llama2 LLM类见examples/llama2_for_langchain.py,调用代码如下所示:…...

ES6中数组的扩展
1. 扩展运算符 用三个点(...)表示,它如同rest参数的逆运算,将数组转为用逗号分隔的参数序列。扩展就是将一个集合分成一个个的。 console.log(...[1, 2, 3]); // 1, 2, 3可以用于函数调用 扩展运算符后还可以放置表达式 ...(x > 0 ? [a] : [])如…...
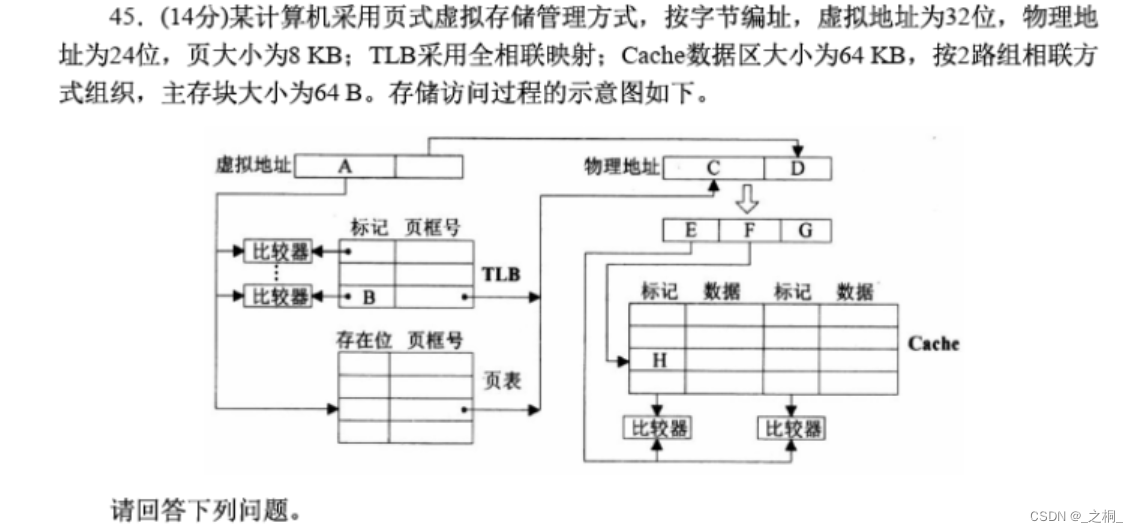
计算机考研 | 2016年 | 计算机组成原理真题
文章目录 【计算机组成原理2016年真题44题-9分】【第一步:信息提取】【第二步:具体解答】 【计算机组成原理2016年真题45题-14分】【第一步:信息提取】【第二步:具体解答】 【计算机组成原理2016年真题44题-9分】 假定CPU主频为5…...
Web版Photoshop来了,用到了哪些前端技术?
经过 Adobe 工程师多年来的努力,并与 Chrome 等浏览器供应商密切合作,通过 WebAssembly Emscripten、Web Components Lit、Service Workers Workbox 和新的 Web API 的支持,终于在近期推出了 Web 版 Photoshop(photoshop.adobe…...

FL Studio21.1.0水果中文官方网站
FL Studio 21.1.0官方中文版重磅发布纯正简体中文支持,更快捷的音频剪辑及素材管理器,多样主题随心换!Mac版新增对苹果M2/1家族芯片原生支持。DAW界萌神!极富二次元造型的水果娘FL chan通过FL插件Fruity Dance登场,为其…...
[BJDCTF2020]Mark loves cat
先用dirsearch扫一下,访问一下没有什么 需要设置线程 dirsearch -u http://8996e81f-a75c-4180-b0ad-226d97ba61b2.node4.buuoj.cn:81/ --timeout2 -t 1 -x 400,403,404,500,503,429使用githack python2 GitHack.py http://8996e81f-a75c-4180-b0ad-226d97ba61b2.…...
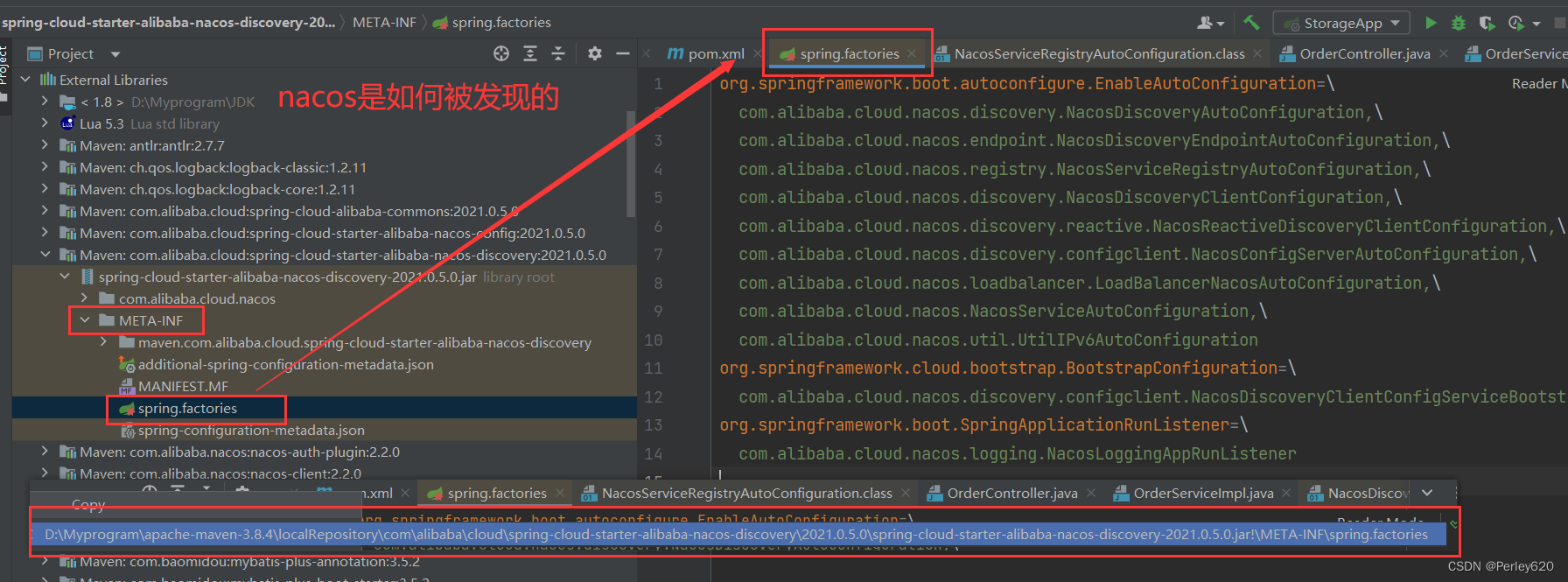
@SpringBootApplication注解的理解——如何排除自动装配 分布式情况下如何自动加载 nacos是怎么被发现的
前言 spring作为主流的 Java Web 开发的开源框架,是Java 世界最为成功的框架,持续不断深入认识spring框架是Java程序员不变的追求。 本篇博客介绍SpringBootApplicant注解的自动加载相关内容 其他相关的Spring博客文章列表如下: Spring基…...

HTTP的前世今生
史前时期 20 世纪 60 年代,美国国防部高等研究计划署(ARPA)建立了 ARPA 网,它有四个分布在各地的节点,被认为是如今互联网的“始祖”。 然后在 70 年代,基于对 ARPA 网的实践和思考,研究人员发…...

软件测试教程 自动化测试selenium篇(二)
掌握Selenium常用的API的使用 目录 一、webdriver API 1.1元素的定位 1.2 id定位 1.3name 定位 1.4tag name 定位和class name 定位 1.5CSS 定位 1.6XPath 定位 1.7link text定位 1.8Partial link text 定位 二、操作测试对象 2.1鼠标点击与键盘输入 2.2submit 提交…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
